《第12章二次根式》课后自主能力提升训练(1) 2020-2021学年八年级数学苏科版下册(word版含解析)
文档属性
| 名称 | 《第12章二次根式》课后自主能力提升训练(1) 2020-2021学年八年级数学苏科版下册(word版含解析) |
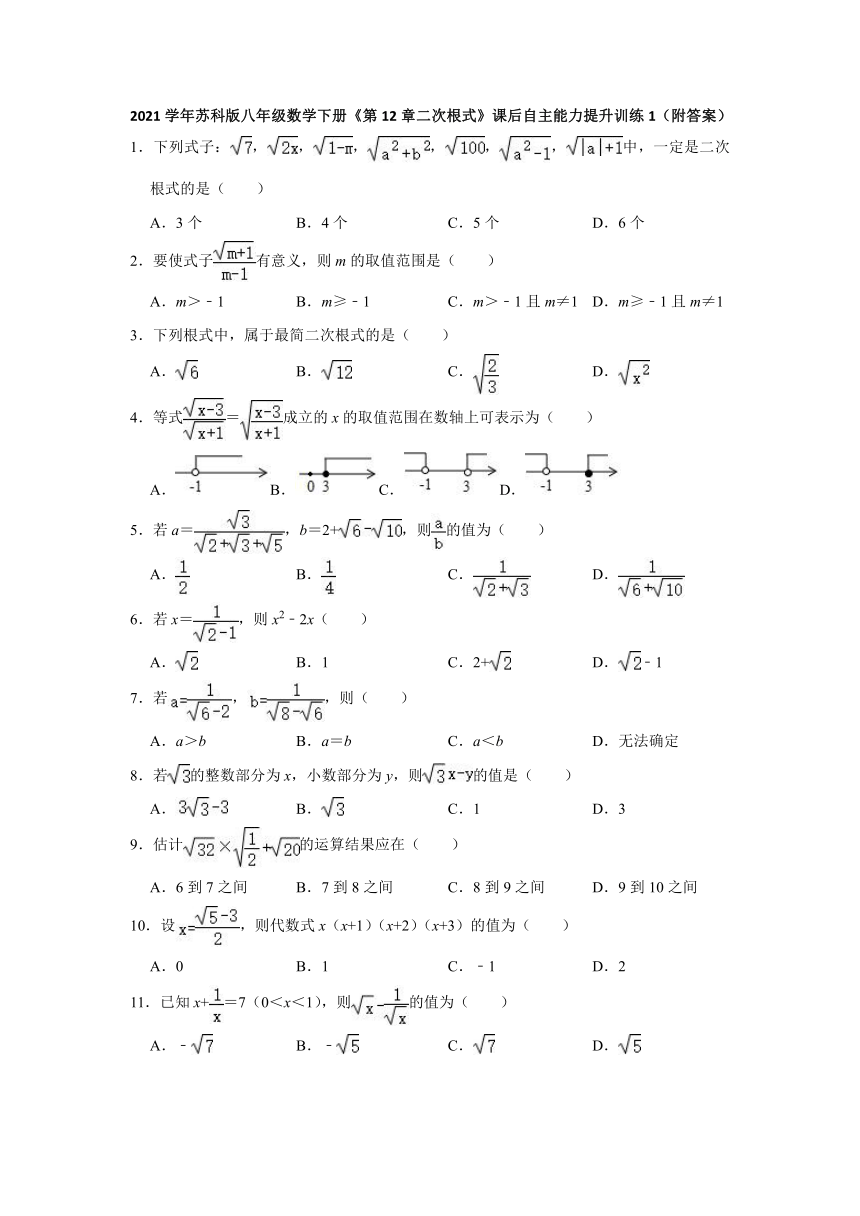
|
|
| 格式 | doc | ||
| 文件大小 | 290.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览
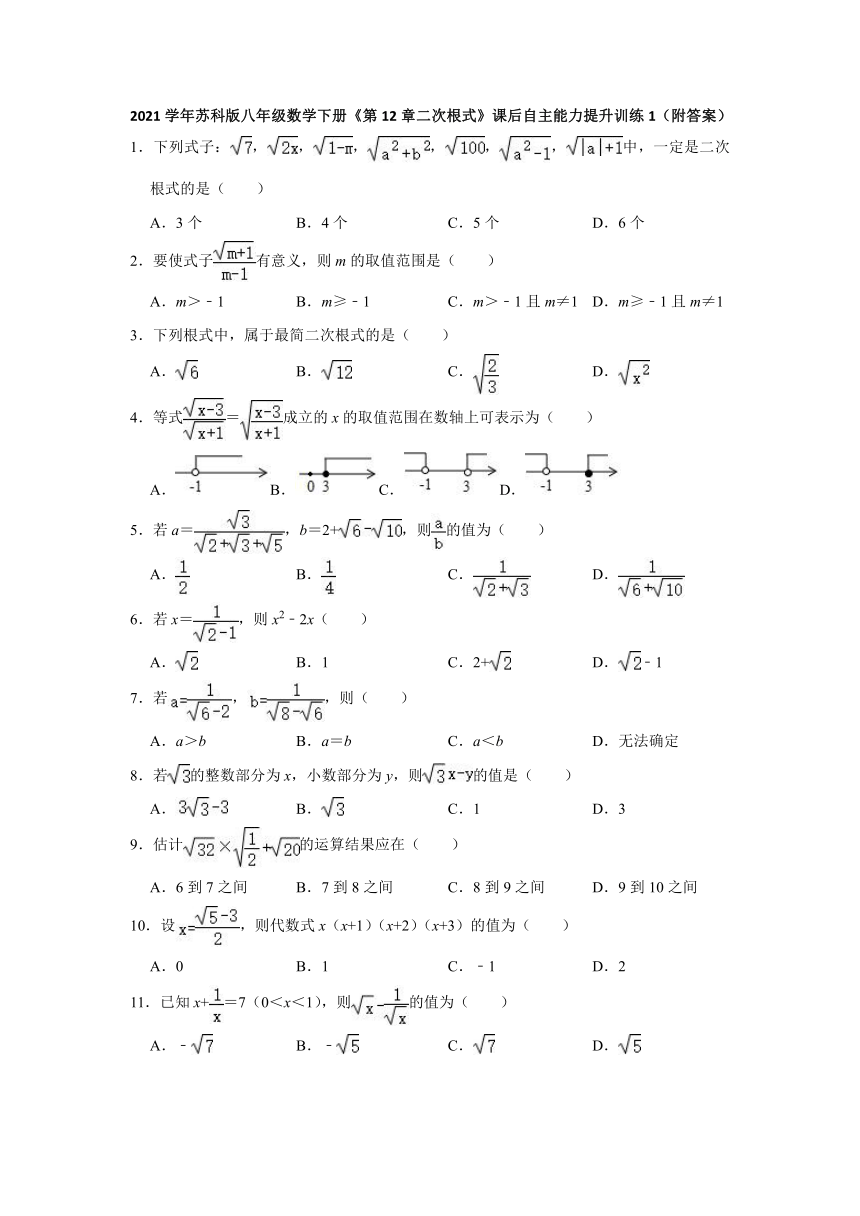




文档简介
2021学年苏科版八年级数学下册《第12章二次根式》课后自主能力提升训练1(附答案)
1.下列式子:,,,,,,中,一定是二次根式的是( )
A.3个 B.4个 C.5个 D.6个
2.要使式子有意义,则m的取值范围是( )
A.m>﹣1 B.m≥﹣1 C.m>﹣1且m≠1 D.m≥﹣1且m≠1
3.下列根式中,属于最简二次根式的是( )
A. B. C. D.
4.等式=成立的x的取值范围在数轴上可表示为( )
A.B.C.D.
5.若a=,b=2+,则的值为( )
A. B. C. D.
6.若x=,则x2﹣2x( )
A. B.1 C.2+ D.﹣1
7.若,,则( )
A.a>b B.a=b C.a<b D.无法确定
8.若的整数部分为x,小数部分为y,则的值是( )
A. B. C.1 D.3
9.估计的运算结果应在( )
A.6到7之间 B.7到8之间 C.8到9之间 D.9到10之间
10.设,则代数式x(x+1)(x+2)(x+3)的值为( )
A.0 B.1 C.﹣1 D.2
11.已知x+=7(0<x<1),则的值为( )
A.﹣ B.﹣ C. D.
12.若0<a<1,,则代数式的值为( )
A.±2 B.﹣2 C.±4 D.4
13.是整数,则最小的正整数a的值是 .
14.若a、b为实数,且b=+4,则a+b= .
15.化简二次根式的正确结果是 .
16.已知a,b,c为三角形的三边,则= .
17.在数轴上表示实数a的点如图所示,化简+|a﹣2|的结果为 .
18.若二次根式是最简二次根式,则最小的正整数a= .
19.分母有理化后的值为 .
20.如果最简二次根式与是同类二次根式,那么a= .
21.当a= 时,最简二次根式与是同类二次根式.
22.如图,正方形ABCD的三个顶点A、B、D分别在长方形EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为,,则正方形ABCD的面积为 .
若|2017﹣m|+=m,则m﹣20172= .
24.已知+()2=2000,y=++,求y﹣x的平方根.
25.先化简,再求值:6x2+2xy﹣8y2﹣2(3xy﹣4y2+3x2),其中x=,y=.
26.计算:
(1)÷
(2)÷3×
27.计算:
(1)2
(2)﹣(15)(x>0)
28.计算:
(1)(2﹣6+3)÷2;
(2)(2+5)(2﹣5)﹣(﹣)2.
29.阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=,那么这个三角形的面积S=.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式.中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦﹣﹣﹣九韶公式”完成下列问题:
如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1+h2的值.
30.阅读下列解题过程:,,
请回答下列问题:
(1)观察上面的解答过程,请直接写出= ;
(2)根据上面的解法,请化简:
.
参考答案
1.解:在所列式子中,一定是二次根式的是,,,这4个,
故选:B.
2.解:根据题意得:,
解得:m≥﹣1且m≠1.
故选:D.
3.解:A.是最简二次根式,符合题意;
B.==2,不符合题意;
C.=,不符合题意;
D.=|x|,不符合题意.
故选:A.
4.解:由题意可知:
解得:x≥3
故选:B.
5.解:a=?=.
∴.
故选:B.
6.解:∵x==+1,
∴x2﹣2x=x(x﹣2)
=(+1)(+1﹣2)
=2﹣1
=1.
故选:B.
7.解:a===,
b===,
∵>2,=,
∴<,
∴a<b,
故选:C.
8.解:∵的整数部分为1,小数部分为﹣1,
∴x=1,y=﹣1,
∴=﹣(﹣1)=1.
故选:C.
9.解:∵=4+,而4<<5,
∴原式运算的结果在8到9之间;
故选:C.
10.解:∵x=,
∴x+1=,
x+2=,
x+3=,
∴原式=×××
=×
=﹣1×1
=﹣1.
故选:C.
11.解:(﹣)2=x+﹣2=7﹣2=5,
∵0<x<1,
∴<,
∴﹣<0.
∴﹣=﹣.
故选:B.
12.解:∵a+=6,0<a<1,
∴﹣<0,
则(﹣)2=a﹣2=6﹣2=4,
∴﹣=﹣2;
故选:B.
13.解:45a=5×3×3×a,
若为整数,则必能被开方,所以满足条件的最小正整数a为5.
故答案为:5.
14.解:由被开方数是非负数,得
,
解得a=1,或a=﹣1,b=4,
当a=1时,a+b=1+4=5,
当a=﹣1时,a+b=﹣1+4=3,
故答案为:5或3.
15.解:由二次根式的性质得﹣a3b≥0
∵a<b
∴a<0,b>0
∴原式==﹣a.
16.解:∵a,b,c为三角形的三边,
∴a+b>c,c+a>b,b+c>a,
∴a+b﹣c>0,b﹣c﹣a<0,b+c﹣a>0,
∴=|a+b﹣c|+|b﹣c﹣a|+|b+c﹣a|=a+b﹣c+a+c﹣b+b+c﹣a=a+b+c.
故答案为:a+b+c.
17.解:由数轴可得:a﹣5<0,a﹣2>0,
则+|a﹣2|
=5﹣a+a﹣2
=3.
故答案为:3.
18.解:二次根式是最简二次根式,则最小的正整数a=2,
故答案为:2.
19.解:===+1,
故答案为:.
20.解:∵最简二次根式与是同类二次根式,
∴1+a=4a﹣2,
解得a=1.
故答案为1.
21.解:∵最简二次根式与是同类二次根式,
∴a2﹣3=1﹣3a,a2﹣3≥0,1﹣3a≥0,
解得:a=﹣4.
故答案为:﹣4.
22.解:过C作MN∥HG交EH于M,交FG于N,CS⊥HG于S,
则四边形MNGH、四边形MCSH、四边形CNGS是矩形,
∴∠HMC=∠GNC=90°,MH=CS=NG=1,
∴∠DMC=∠BNC=90°,
∵CH=,CG=,
∴CM2=4,CN2=9,
∵四边形ABCD是正方形,
∴CD=BC,∠BCD=90°,
∴∠CDM+∠DCM=∠DCM+∠BCN=90°,
∴∠CDM=∠BCN,
在△DCM与△CBN中,
∴△DCM≌△CBN(AAS),
∴DM=CN,
∴CD2=DM2+CM2=CN2+CM2=13,
∴正方形ABCD的面积=CD2=13,
故答案为:13.
23.解:∵|2017﹣m|+=m,
∴m﹣2018≥0,
m≥2018,
由题意,得m﹣2017+=m.
化简,得=2017,
平方,得m﹣2018=20172,
m﹣20172=2018.
故答案为:2018.
24.解:由题意得,998﹣x≥0,
解得x≤998,
所以,1000﹣x+998﹣x=2000,
解得x=﹣1,
由题意得,m﹣1≥0且1﹣m≥0,
解得m≥1且m≤1,
所以,m=1,
y==3,
所以,y﹣x=3﹣(﹣1)=3+1=4,
∵(±2)2=4,
∴4的平方根是±2,
即y﹣x的平方根是±2.
25.解:原式=6x2+2xy﹣8y2﹣6xy+8y2﹣6x2
=(6x2﹣6x2)+(2xy﹣6xy)+(﹣8y2+8y2)
=﹣4xy.
当x=,y=时,
原式=﹣4××
=﹣8.
26.解:(1)÷
=×
=
=;
(2)÷3×
=××
=
=.
27.解:(1)原式=2+6﹣4
=4;
(2)原式=﹣(15×﹣2x)
=3﹣3+2x
=2x.
28.解:(1)(2﹣6+3)÷2;
=(4﹣2+12)÷2
=14÷2
=7
(2)(2+5)(2﹣5)﹣(﹣)2.
=(2)2﹣(5)2﹣(5﹣2+2)
=20﹣50﹣(7﹣2)
═﹣37+2.
29.解.(1)根据题意知p==9
所以S===6
∴△ABC的面积为6;
(2)∵S=ch1=bh2=6
∴×6h1=×5h2=6
∴h1=2,h2=
∴h1+h2=.
30.解:(1)=﹣;
(2)+++…++,
=﹣1+﹣+﹣+…+﹣+﹣,
=﹣1,
=10﹣1,
=9.
故答案为:(1)﹣,(2)9.
1.下列式子:,,,,,,中,一定是二次根式的是( )
A.3个 B.4个 C.5个 D.6个
2.要使式子有意义,则m的取值范围是( )
A.m>﹣1 B.m≥﹣1 C.m>﹣1且m≠1 D.m≥﹣1且m≠1
3.下列根式中,属于最简二次根式的是( )
A. B. C. D.
4.等式=成立的x的取值范围在数轴上可表示为( )
A.B.C.D.
5.若a=,b=2+,则的值为( )
A. B. C. D.
6.若x=,则x2﹣2x( )
A. B.1 C.2+ D.﹣1
7.若,,则( )
A.a>b B.a=b C.a<b D.无法确定
8.若的整数部分为x,小数部分为y,则的值是( )
A. B. C.1 D.3
9.估计的运算结果应在( )
A.6到7之间 B.7到8之间 C.8到9之间 D.9到10之间
10.设,则代数式x(x+1)(x+2)(x+3)的值为( )
A.0 B.1 C.﹣1 D.2
11.已知x+=7(0<x<1),则的值为( )
A.﹣ B.﹣ C. D.
12.若0<a<1,,则代数式的值为( )
A.±2 B.﹣2 C.±4 D.4
13.是整数,则最小的正整数a的值是 .
14.若a、b为实数,且b=+4,则a+b= .
15.化简二次根式的正确结果是 .
16.已知a,b,c为三角形的三边,则= .
17.在数轴上表示实数a的点如图所示,化简+|a﹣2|的结果为 .
18.若二次根式是最简二次根式,则最小的正整数a= .
19.分母有理化后的值为 .
20.如果最简二次根式与是同类二次根式,那么a= .
21.当a= 时,最简二次根式与是同类二次根式.
22.如图,正方形ABCD的三个顶点A、B、D分别在长方形EFGH的边EF、FG、EH上,且C到HG的距离是1,到点H,G的距离分别为,,则正方形ABCD的面积为 .
若|2017﹣m|+=m,则m﹣20172= .
24.已知+()2=2000,y=++,求y﹣x的平方根.
25.先化简,再求值:6x2+2xy﹣8y2﹣2(3xy﹣4y2+3x2),其中x=,y=.
26.计算:
(1)÷
(2)÷3×
27.计算:
(1)2
(2)﹣(15)(x>0)
28.计算:
(1)(2﹣6+3)÷2;
(2)(2+5)(2﹣5)﹣(﹣)2.
29.阅读材料:
如果一个三角形的三边长分别为a,b,c,记p=,那么这个三角形的面积S=.这个公式叫“海伦公式”,它是利用三角形三条边的边长直接求三角形面积的公式.中国的秦九韶也得出了类似的公式,称三斜求积术,故这个公式又被称为“海伦秦﹣﹣﹣九韶公式”完成下列问题:
如图,在△ABC中,a=7,b=5,c=6.
(1)求△ABC的面积;
(2)设AB边上的高为h1,AC边上的高为h2,求h1+h2的值.
30.阅读下列解题过程:,,
请回答下列问题:
(1)观察上面的解答过程,请直接写出= ;
(2)根据上面的解法,请化简:
.
参考答案
1.解:在所列式子中,一定是二次根式的是,,,这4个,
故选:B.
2.解:根据题意得:,
解得:m≥﹣1且m≠1.
故选:D.
3.解:A.是最简二次根式,符合题意;
B.==2,不符合题意;
C.=,不符合题意;
D.=|x|,不符合题意.
故选:A.
4.解:由题意可知:
解得:x≥3
故选:B.
5.解:a=?=.
∴.
故选:B.
6.解:∵x==+1,
∴x2﹣2x=x(x﹣2)
=(+1)(+1﹣2)
=2﹣1
=1.
故选:B.
7.解:a===,
b===,
∵>2,=,
∴<,
∴a<b,
故选:C.
8.解:∵的整数部分为1,小数部分为﹣1,
∴x=1,y=﹣1,
∴=﹣(﹣1)=1.
故选:C.
9.解:∵=4+,而4<<5,
∴原式运算的结果在8到9之间;
故选:C.
10.解:∵x=,
∴x+1=,
x+2=,
x+3=,
∴原式=×××
=×
=﹣1×1
=﹣1.
故选:C.
11.解:(﹣)2=x+﹣2=7﹣2=5,
∵0<x<1,
∴<,
∴﹣<0.
∴﹣=﹣.
故选:B.
12.解:∵a+=6,0<a<1,
∴﹣<0,
则(﹣)2=a﹣2=6﹣2=4,
∴﹣=﹣2;
故选:B.
13.解:45a=5×3×3×a,
若为整数,则必能被开方,所以满足条件的最小正整数a为5.
故答案为:5.
14.解:由被开方数是非负数,得
,
解得a=1,或a=﹣1,b=4,
当a=1时,a+b=1+4=5,
当a=﹣1时,a+b=﹣1+4=3,
故答案为:5或3.
15.解:由二次根式的性质得﹣a3b≥0
∵a<b
∴a<0,b>0
∴原式==﹣a.
16.解:∵a,b,c为三角形的三边,
∴a+b>c,c+a>b,b+c>a,
∴a+b﹣c>0,b﹣c﹣a<0,b+c﹣a>0,
∴=|a+b﹣c|+|b﹣c﹣a|+|b+c﹣a|=a+b﹣c+a+c﹣b+b+c﹣a=a+b+c.
故答案为:a+b+c.
17.解:由数轴可得:a﹣5<0,a﹣2>0,
则+|a﹣2|
=5﹣a+a﹣2
=3.
故答案为:3.
18.解:二次根式是最简二次根式,则最小的正整数a=2,
故答案为:2.
19.解:===+1,
故答案为:.
20.解:∵最简二次根式与是同类二次根式,
∴1+a=4a﹣2,
解得a=1.
故答案为1.
21.解:∵最简二次根式与是同类二次根式,
∴a2﹣3=1﹣3a,a2﹣3≥0,1﹣3a≥0,
解得:a=﹣4.
故答案为:﹣4.
22.解:过C作MN∥HG交EH于M,交FG于N,CS⊥HG于S,
则四边形MNGH、四边形MCSH、四边形CNGS是矩形,
∴∠HMC=∠GNC=90°,MH=CS=NG=1,
∴∠DMC=∠BNC=90°,
∵CH=,CG=,
∴CM2=4,CN2=9,
∵四边形ABCD是正方形,
∴CD=BC,∠BCD=90°,
∴∠CDM+∠DCM=∠DCM+∠BCN=90°,
∴∠CDM=∠BCN,
在△DCM与△CBN中,
∴△DCM≌△CBN(AAS),
∴DM=CN,
∴CD2=DM2+CM2=CN2+CM2=13,
∴正方形ABCD的面积=CD2=13,
故答案为:13.
23.解:∵|2017﹣m|+=m,
∴m﹣2018≥0,
m≥2018,
由题意,得m﹣2017+=m.
化简,得=2017,
平方,得m﹣2018=20172,
m﹣20172=2018.
故答案为:2018.
24.解:由题意得,998﹣x≥0,
解得x≤998,
所以,1000﹣x+998﹣x=2000,
解得x=﹣1,
由题意得,m﹣1≥0且1﹣m≥0,
解得m≥1且m≤1,
所以,m=1,
y==3,
所以,y﹣x=3﹣(﹣1)=3+1=4,
∵(±2)2=4,
∴4的平方根是±2,
即y﹣x的平方根是±2.
25.解:原式=6x2+2xy﹣8y2﹣6xy+8y2﹣6x2
=(6x2﹣6x2)+(2xy﹣6xy)+(﹣8y2+8y2)
=﹣4xy.
当x=,y=时,
原式=﹣4××
=﹣8.
26.解:(1)÷
=×
=
=;
(2)÷3×
=××
=
=.
27.解:(1)原式=2+6﹣4
=4;
(2)原式=﹣(15×﹣2x)
=3﹣3+2x
=2x.
28.解:(1)(2﹣6+3)÷2;
=(4﹣2+12)÷2
=14÷2
=7
(2)(2+5)(2﹣5)﹣(﹣)2.
=(2)2﹣(5)2﹣(5﹣2+2)
=20﹣50﹣(7﹣2)
═﹣37+2.
29.解.(1)根据题意知p==9
所以S===6
∴△ABC的面积为6;
(2)∵S=ch1=bh2=6
∴×6h1=×5h2=6
∴h1=2,h2=
∴h1+h2=.
30.解:(1)=﹣;
(2)+++…++,
=﹣1+﹣+﹣+…+﹣+﹣,
=﹣1,
=10﹣1,
=9.
故答案为:(1)﹣,(2)9.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
