20.2.1方差-2020-2021学年人教版八年级数学下册导学案(Word版含详解)
文档属性
| 名称 | 20.2.1方差-2020-2021学年人教版八年级数学下册导学案(Word版含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 08:44:35 | ||
图片预览



文档简介
20.2数据的波动程度
第一课时 方差
学习目标:
1.弄清楚方差的概念及其统计学意义.
2.会计算一组数据的方差.
3.能够运用方差判断数据的波动程度.
学习重点:弄清方差的意义,会计算一组数据的方差.
一、课前检测
1.某超市购进一批不同价格的皮鞋,下表是该超市在近几年统计的平均数据.要使该超市销售皮鞋收入最大,该超市应多购( )的皮鞋。
皮鞋价(元) 160 140 120 100
销售百分率 60% 75% 83% 95%
A.160元 B.140元 C.120元 D.100元
2.已知一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的中位数是_______.
二、温故知新
1.在前面你已经学过哪些统计量,它们各有何特点?
2.如何求一组数据的平均数?平均数在反映数据的整体水平有什么局限性?
三、预习导航(预习教材第124-126页,标出你认为重要的关键词)
1.刘教练到我班选拔一名篮球队员,刘教练对陈楷和李东两名学生进行5次投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
队??员 第?1次 第2次 第3次 第4次 第5次
陈楷 7 8 8 8 9
李东 10 6 10 6 8
(1)请求出以上两组数据的平均数、中位数、众数;
(2)用复式折线统计图表示上述数据;
(3)若要选一个投篮稳定的队员,选谁更好?
2.自主归纳:
(1)统计中,常用 来衡量一组数据的波动大小;
(2)设有n个数据,各数据与它们的平均数的差的平方分别是
,我们用它们的平均数,表示这组数据的方差,即用s2= 来表示.
四、自学自测
1.计算下列各组数据的方差:
(1)6 6 6 6 6 6; (2)5 5 6 6 7 7.
2.五个数1,3,a,5,8的平均数是4,则a =_____,这五个数的方差_____.
五、我的疑惑(反思)
_________________________________________________________________________
要点探究
探究点1:方差的意义
问题1:农科院计划为某地选择合适的甜玉米种子. 选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表.根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
(1)甜玉米的产量可用什么量来描述?请计算后说明.
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
②请利用方差公式分析甲、乙两种甜玉米的波动程度.
要点归纳
1.方差用来衡量一组数据的 (即这组数据偏离 的大小).
2.方差越大,数据的波动 ;方差越小,数据的波动 .
二、精讲点拨
问题2:在某次篮球联赛中,最后是九班和三班争夺这次篮球赛冠军, 赛前两个班的拉拉队都表演了啦啦操,参加表演的女同学的身高(单位:cm)分别是:
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
哪班啦啦操队女同学的身高更整齐?
(1)你是如何理解“整齐”的?
(2)从数据上看,你是如何判断那个队更整齐?
问题3:已知数据x1、x2、…、xn的平均数为,方差为s2.
(1)x1+b、x2+b、…、xn+b的平均数为 ,方差为 ;
(2)ax1、ax2、…、axn的平均数为 ,方差为 ;
(3)ax1+b、ax2+b、…、axn+b的平均数为 ,方差为 .
三、变式训练
1.计算并比较两组数据的平均数和方差,体会方差是怎样刻画数据的波动程度的.
(1)3 3 4 6 8 9 9; (2)3 3 3 6 9 9 9.
2.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有 .
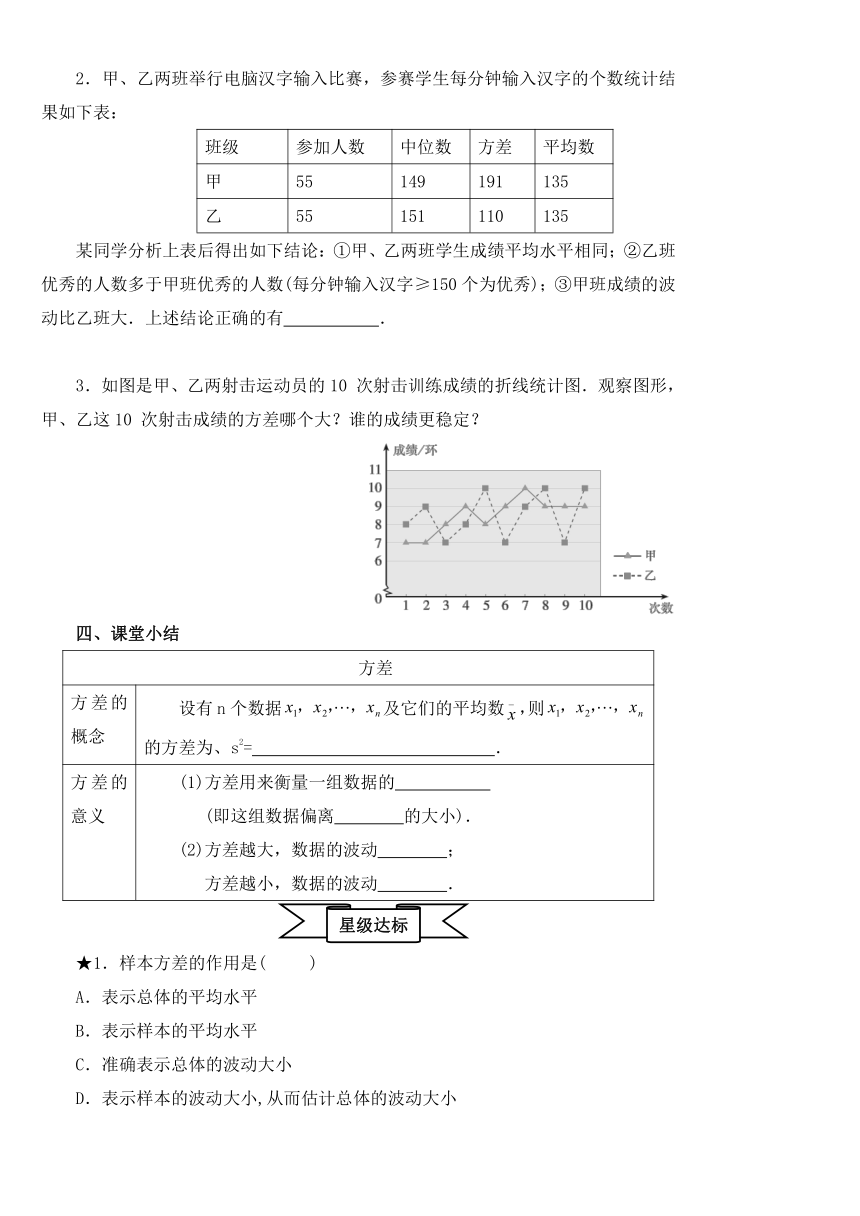
3.如图是甲、乙两射击运动员的10 次射击训练成绩的折线统计图.观察图形,甲、乙这10 次射击成绩的方差哪个大?谁的成绩更稳定?
四、课堂小结
方差
方差的概念 设有n个数据及它们的平均数,则的方差为、s2= .
方差的意义 (1)方差用来衡量一组数据的
(即这组数据偏离 的大小).
(2)方差越大,数据的波动 ;
方差越小,数据的波动 .
★1.样本方差的作用是( )
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
★2.人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:,, ,则成绩较为稳定的班级是( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
★3.在样本方差的计算公式 中, 数字10 表示___________ ,数字20表示 _______.
★4.小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图所示,则他这五次成绩的方差为 .
★★5.若样本的平均数是10,方差是3,则样本2+1,2+1,…,2+1的平均数和方差分别为___________.
★★6.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84
84
0.3
乙 84 84
34
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测:
1.试题分析:本题考查的是统计的应用,分别求出每种皮鞋的销售额,再比较即可.
详解:设每种皮鞋都有a双.四种皮鞋的销售额分别为:
;
;
;
.
可见应多购140元的皮鞋.
故选B.
2.试题分析:先判断出x,y中至少有一个是5,再用平均数求出x+y=11,即可得出结论.
详解:∵一组数据4,x,5,y,7,9的众数为5,
∴x,y中至少有一个是5,
∵一组数据4,x,5,y,7,9的平均数为6,
∴(4+x+5+y+7+9)=6,
∴x+y=11,
∴x,y中一个是5,另一个是6,
∴这组数为4,5,5,6,7,9,
∴这组数据的中位数是×(5+6)=5.5,
故答案为5.5.
自学自测
1.试题分析:根据方差公式进行计算即可.
详解:(1)=6,
∴=[(6-6)+(6-6)+(6-6)+(6-6)+(6-6)+(6-6)]=×0=0.
(2)=6,
∴=[(5-6)+(5-6)+(6-6)+(6-6)+(7-6)+(7-6)]=×4=.
2.试题分析:先根据平均数的公式计算出a的值,再根据方差的公式计算.
详解:由题意知:a=4×5﹣(1+3+5+8)=3,
这五个数的方差S2=[(1﹣4)2+(3﹣4)2+(3﹣4)2+(5﹣4)2+(8﹣4)2]=5.6.
故答案为3;5.6.
变式训练
1.试题分析:先根据平均数的公式计算出两组数据的平均数,再根据方差的公式计算即可.
详解:(1)=6,
∴=[(3-6)+(3-6)+(4-6)+(6-6)+(8-6)+(9-6)+(9-6)]=×44=.
(2)=6,
∴=[(3-6)+(3-6)+(3-6)+(6-6)+(9-6)+(9-6)+(9-6)]=×54=.
通过计算可以看出,两组数据的平均数相同,(1)组的方差小于(2)组的方差,说明(1)组数据比(2)组数据波动小.
试题分析:根据表格中中位数、方差、平均数的数据分别对几个结论进行判断即可.
详解:∵甲=乙,∴①正确;
∵乙的中位数为151,甲的中位数为149,∴乙班优秀的人数多于甲班优秀的人数②正确;
∵S2甲>S2乙,∴甲班成绩的波动比乙班大,③正确;
故正确的结论是①②③.
3.试题分析:根据折线统计图提供的数据,先算出甲乙成绩的方差,然后进行比较即可.
详解:由图中知,甲的成绩为7,7,8,9,8,9,10,9,9,9,
乙的成绩为8,9,7,8,10,7,9,10,7,10,
甲=(7+7+8+9+8+9+10+9+9+9)÷10=8.5,
乙=(8+9+7+8+10+7+9+10+7+10)÷10=8.5,
甲的方差S甲2=[2×(7-8.5)2+2×(8-8.5)2+(10-8.5)2+5×(9-8.5)2]÷10=0.85,
乙的方差S乙2=[3×(7-8.5)2+2×(8-8.5)2+2×(9-8.5)2+3×(10-8.5)2]÷10=1.35
∴S2甲<S2乙.甲运动员的成绩更稳定些.
星级达标:
1.试题分析:根据样本方差的意义即可做出判断.
详解:一组数据的方差反映这组数据的波动情况,从而能估计总体的波动大小.
故选答案D.
2.试题分析:∵,说明甲乙的平均成绩相同;∵, ,s甲2>s乙2,∴乙班的成绩较为稳定.
详解:∵, ,s甲2>s乙2,∴乙班的成绩较为稳定.
故选B.
3.试题分析:方差计算公式:S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]中,n表示样本容量,为平均数,根据此公式即可得到答案.
详解:由于s2=[(x1﹣20)2+(x2﹣20)2+…+(x10﹣20)2],所以样本容量是10,平均数是20.
故答案为:样本容量,平均数.
4.试题分析:根据折线统计图提供的数据,先算出小凯成绩的平均数,然后代入方差公式计算即可.
详解:由折线图可知,小凯的成绩为55,70,65,75,85.
=(55+70+65+75+85)÷5=70;
∴方差S2=[(55-70)2+(70-70)2+(65-70)2+(75-70)2+(85-70)2]=100.
故答案为:100.
5.试题分析:利用平均数与方差的性质分别分析得出即可.
详解:∵样本x1,x2,…,xn的平均数为10,方差为3,
∴(2x1+1),(2x2+1),(2x3+1),…,(2xn+1)的平均数为2×10+1=21,方差为22×3=12.
故答案为21和12.
6.试题分析:根据中位数的定义找出最中间两个数的平均数,根据众数的定义找出出现次数最多的数,频率是用85分以上的频数除以总数即可.
详解:(1)
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 84 14.4 0.3
乙 84 84 90 34 0.5
(2)甲成绩的众数是84,乙成绩的众数是90,从两人成绩的众数看,乙的成绩较好.
甲成绩的方差是14.4,乙成绩的方差是34,从成绩的方差看,甲的成绩相对稳定.
甲成绩、乙成绩的中位数、平均数都是84,但从85分以上的频率看,乙的成绩较好.
第一课时 方差
学习目标:
1.弄清楚方差的概念及其统计学意义.
2.会计算一组数据的方差.
3.能够运用方差判断数据的波动程度.
学习重点:弄清方差的意义,会计算一组数据的方差.
一、课前检测
1.某超市购进一批不同价格的皮鞋,下表是该超市在近几年统计的平均数据.要使该超市销售皮鞋收入最大,该超市应多购( )的皮鞋。
皮鞋价(元) 160 140 120 100
销售百分率 60% 75% 83% 95%
A.160元 B.140元 C.120元 D.100元
2.已知一组数据4,x,5,y,7,9的平均数为6,众数为5,则这组数据的中位数是_______.
二、温故知新
1.在前面你已经学过哪些统计量,它们各有何特点?
2.如何求一组数据的平均数?平均数在反映数据的整体水平有什么局限性?
三、预习导航(预习教材第124-126页,标出你认为重要的关键词)
1.刘教练到我班选拔一名篮球队员,刘教练对陈楷和李东两名学生进行5次投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
队??员 第?1次 第2次 第3次 第4次 第5次
陈楷 7 8 8 8 9
李东 10 6 10 6 8
(1)请求出以上两组数据的平均数、中位数、众数;
(2)用复式折线统计图表示上述数据;
(3)若要选一个投篮稳定的队员,选谁更好?
2.自主归纳:
(1)统计中,常用 来衡量一组数据的波动大小;
(2)设有n个数据,各数据与它们的平均数的差的平方分别是
,我们用它们的平均数,表示这组数据的方差,即用s2= 来表示.
四、自学自测
1.计算下列各组数据的方差:
(1)6 6 6 6 6 6; (2)5 5 6 6 7 7.
2.五个数1,3,a,5,8的平均数是4,则a =_____,这五个数的方差_____.
五、我的疑惑(反思)
_________________________________________________________________________
要点探究
探究点1:方差的意义
问题1:农科院计划为某地选择合适的甜玉米种子. 选择种子时,甜玉米的产量和产量的稳定性是农科院所关心的问题.为了解甲、乙两种甜玉米种子的相关情况,农科院各用10 块自然条件相同的试验田进行试验,得到各试验田每公顷的产量(单位:t)如下表.根据这些数据估计,农科院应该选择哪种甜玉米种子呢?
(1)甜玉米的产量可用什么量来描述?请计算后说明.
(2)如何考察一种甜玉米产量的稳定性呢?
①请设计统计图直观地反映出甜玉米产量的分布情况.
②请利用方差公式分析甲、乙两种甜玉米的波动程度.
要点归纳
1.方差用来衡量一组数据的 (即这组数据偏离 的大小).
2.方差越大,数据的波动 ;方差越小,数据的波动 .
二、精讲点拨
问题2:在某次篮球联赛中,最后是九班和三班争夺这次篮球赛冠军, 赛前两个班的拉拉队都表演了啦啦操,参加表演的女同学的身高(单位:cm)分别是:
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
哪班啦啦操队女同学的身高更整齐?
(1)你是如何理解“整齐”的?
(2)从数据上看,你是如何判断那个队更整齐?
问题3:已知数据x1、x2、…、xn的平均数为,方差为s2.
(1)x1+b、x2+b、…、xn+b的平均数为 ,方差为 ;
(2)ax1、ax2、…、axn的平均数为 ,方差为 ;
(3)ax1+b、ax2+b、…、axn+b的平均数为 ,方差为 .
三、变式训练
1.计算并比较两组数据的平均数和方差,体会方差是怎样刻画数据的波动程度的.
(1)3 3 4 6 8 9 9; (2)3 3 3 6 9 9 9.
2.甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 参加人数 中位数 方差 平均数
甲 55 149 191 135
乙 55 151 110 135
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有 .
3.如图是甲、乙两射击运动员的10 次射击训练成绩的折线统计图.观察图形,甲、乙这10 次射击成绩的方差哪个大?谁的成绩更稳定?
四、课堂小结
方差
方差的概念 设有n个数据及它们的平均数,则的方差为、s2= .
方差的意义 (1)方差用来衡量一组数据的
(即这组数据偏离 的大小).
(2)方差越大,数据的波动 ;
方差越小,数据的波动 .
★1.样本方差的作用是( )
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
★2.人数相同的八年级甲、乙两班学生在同一次数学单元测试中,班级平均分和方差如下:,, ,则成绩较为稳定的班级是( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
★3.在样本方差的计算公式 中, 数字10 表示___________ ,数字20表示 _______.
★4.小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图所示,则他这五次成绩的方差为 .
★★5.若样本的平均数是10,方差是3,则样本2+1,2+1,…,2+1的平均数和方差分别为___________.
★★6.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩 76 84 90 84 81 87 88 81 85 84
乙的成绩 82 86 87 90 79 81 93 90 74 78
(1)填写下表:
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84
84
0.3
乙 84 84
34
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
我的反思(收获,不足)
分层作业
必做(教材 智慧学习 配套) 选做
参考答案:
课前检测:
1.试题分析:本题考查的是统计的应用,分别求出每种皮鞋的销售额,再比较即可.
详解:设每种皮鞋都有a双.四种皮鞋的销售额分别为:
;
;
;
.
可见应多购140元的皮鞋.
故选B.
2.试题分析:先判断出x,y中至少有一个是5,再用平均数求出x+y=11,即可得出结论.
详解:∵一组数据4,x,5,y,7,9的众数为5,
∴x,y中至少有一个是5,
∵一组数据4,x,5,y,7,9的平均数为6,
∴(4+x+5+y+7+9)=6,
∴x+y=11,
∴x,y中一个是5,另一个是6,
∴这组数为4,5,5,6,7,9,
∴这组数据的中位数是×(5+6)=5.5,
故答案为5.5.
自学自测
1.试题分析:根据方差公式进行计算即可.
详解:(1)=6,
∴=[(6-6)+(6-6)+(6-6)+(6-6)+(6-6)+(6-6)]=×0=0.
(2)=6,
∴=[(5-6)+(5-6)+(6-6)+(6-6)+(7-6)+(7-6)]=×4=.
2.试题分析:先根据平均数的公式计算出a的值,再根据方差的公式计算.
详解:由题意知:a=4×5﹣(1+3+5+8)=3,
这五个数的方差S2=[(1﹣4)2+(3﹣4)2+(3﹣4)2+(5﹣4)2+(8﹣4)2]=5.6.
故答案为3;5.6.
变式训练
1.试题分析:先根据平均数的公式计算出两组数据的平均数,再根据方差的公式计算即可.
详解:(1)=6,
∴=[(3-6)+(3-6)+(4-6)+(6-6)+(8-6)+(9-6)+(9-6)]=×44=.
(2)=6,
∴=[(3-6)+(3-6)+(3-6)+(6-6)+(9-6)+(9-6)+(9-6)]=×54=.
通过计算可以看出,两组数据的平均数相同,(1)组的方差小于(2)组的方差,说明(1)组数据比(2)组数据波动小.
试题分析:根据表格中中位数、方差、平均数的数据分别对几个结论进行判断即可.
详解:∵甲=乙,∴①正确;
∵乙的中位数为151,甲的中位数为149,∴乙班优秀的人数多于甲班优秀的人数②正确;
∵S2甲>S2乙,∴甲班成绩的波动比乙班大,③正确;
故正确的结论是①②③.
3.试题分析:根据折线统计图提供的数据,先算出甲乙成绩的方差,然后进行比较即可.
详解:由图中知,甲的成绩为7,7,8,9,8,9,10,9,9,9,
乙的成绩为8,9,7,8,10,7,9,10,7,10,
甲=(7+7+8+9+8+9+10+9+9+9)÷10=8.5,
乙=(8+9+7+8+10+7+9+10+7+10)÷10=8.5,
甲的方差S甲2=[2×(7-8.5)2+2×(8-8.5)2+(10-8.5)2+5×(9-8.5)2]÷10=0.85,
乙的方差S乙2=[3×(7-8.5)2+2×(8-8.5)2+2×(9-8.5)2+3×(10-8.5)2]÷10=1.35
∴S2甲<S2乙.甲运动员的成绩更稳定些.
星级达标:
1.试题分析:根据样本方差的意义即可做出判断.
详解:一组数据的方差反映这组数据的波动情况,从而能估计总体的波动大小.
故选答案D.
2.试题分析:∵,说明甲乙的平均成绩相同;∵, ,s甲2>s乙2,∴乙班的成绩较为稳定.
详解:∵, ,s甲2>s乙2,∴乙班的成绩较为稳定.
故选B.
3.试题分析:方差计算公式:S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2]中,n表示样本容量,为平均数,根据此公式即可得到答案.
详解:由于s2=[(x1﹣20)2+(x2﹣20)2+…+(x10﹣20)2],所以样本容量是10,平均数是20.
故答案为:样本容量,平均数.
4.试题分析:根据折线统计图提供的数据,先算出小凯成绩的平均数,然后代入方差公式计算即可.
详解:由折线图可知,小凯的成绩为55,70,65,75,85.
=(55+70+65+75+85)÷5=70;
∴方差S2=[(55-70)2+(70-70)2+(65-70)2+(75-70)2+(85-70)2]=100.
故答案为:100.
5.试题分析:利用平均数与方差的性质分别分析得出即可.
详解:∵样本x1,x2,…,xn的平均数为10,方差为3,
∴(2x1+1),(2x2+1),(2x3+1),…,(2xn+1)的平均数为2×10+1=21,方差为22×3=12.
故答案为21和12.
6.试题分析:根据中位数的定义找出最中间两个数的平均数,根据众数的定义找出出现次数最多的数,频率是用85分以上的频数除以总数即可.
详解:(1)
同学 平均成绩 中位数 众数 方差 85分以上的频率
甲 84 84 84 14.4 0.3
乙 84 84 90 34 0.5
(2)甲成绩的众数是84,乙成绩的众数是90,从两人成绩的众数看,乙的成绩较好.
甲成绩的方差是14.4,乙成绩的方差是34,从成绩的方差看,甲的成绩相对稳定.
甲成绩、乙成绩的中位数、平均数都是84,但从85分以上的频率看,乙的成绩较好.
