北师大版八年级数学下册6.3三角形的中位线课件(共27张PPT)
文档属性
| 名称 | 北师大版八年级数学下册6.3三角形的中位线课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-07 23:58:41 | ||
图片预览


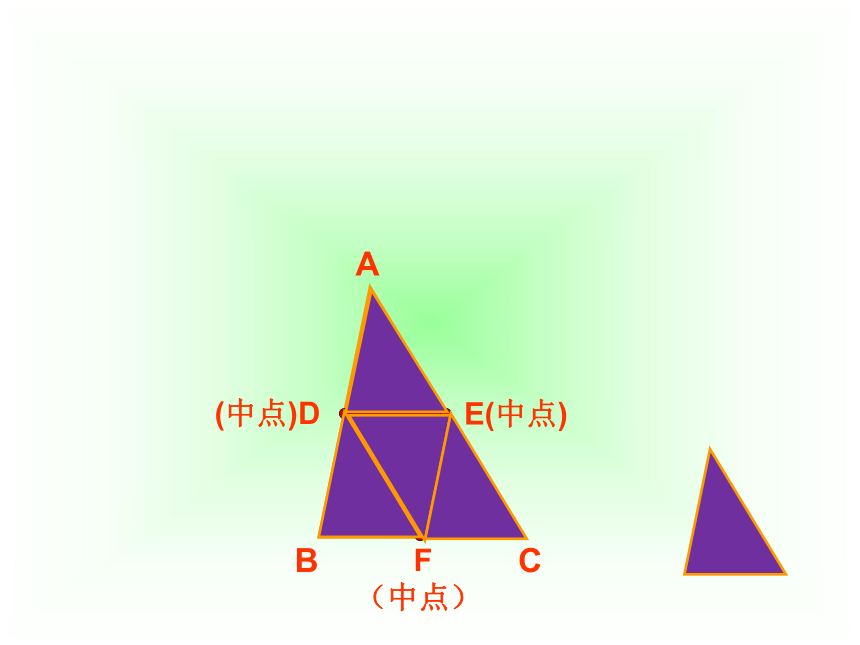
文档简介
(共27张PPT)
6.3
三角形的中位线
1、齐头并进
打一数学中的几何名词
(平行)
2、风筝跑了
(线段)
课前游戏
猜一猜
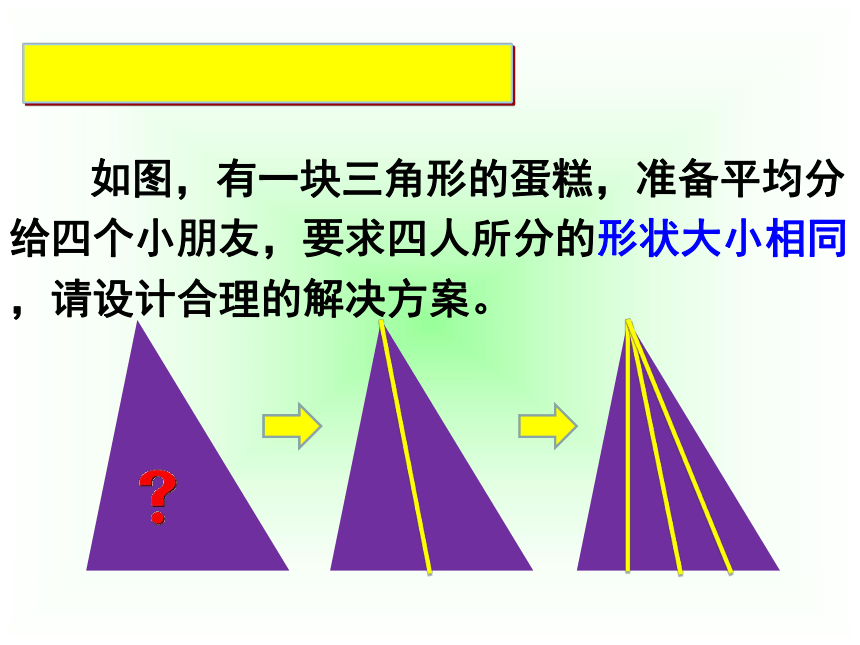
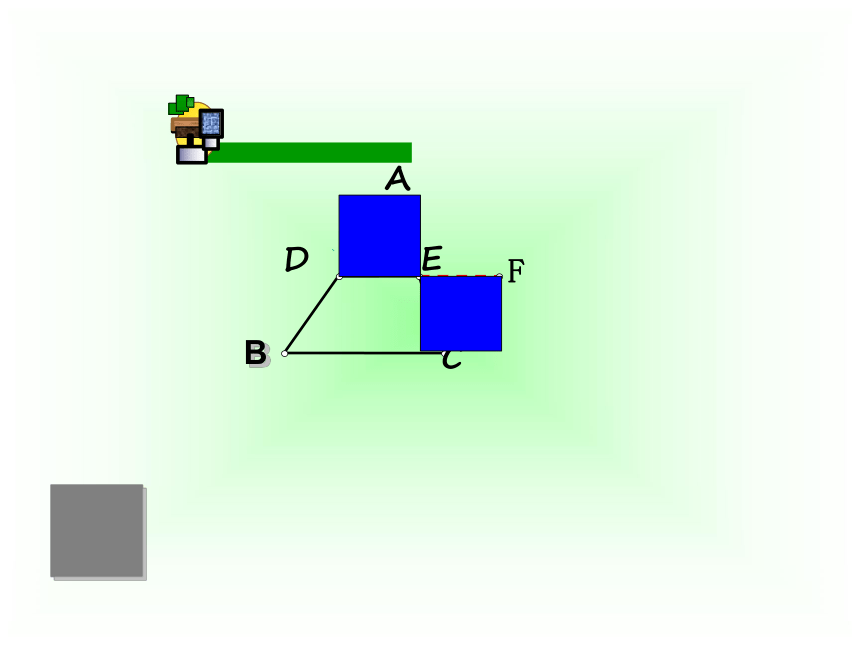
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。
F
(中点)
(中点)D
E(中点)
A
B
C
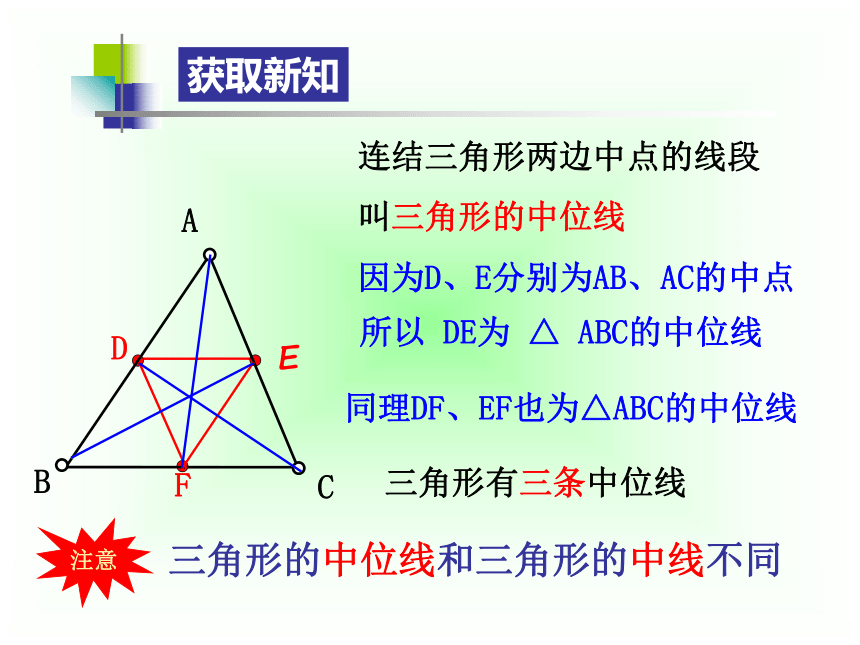
连结三角形两边中点的线段
叫三角形的中位线
三角形有三条中位线
因为D、E分别为AB、AC的中点
三角形的中位线和三角形的中线不同
同理DF、EF也为△ABC的中位线
E
D
F
A
C
B
所以
DE为
△
ABC的中位线
注意
获取新知
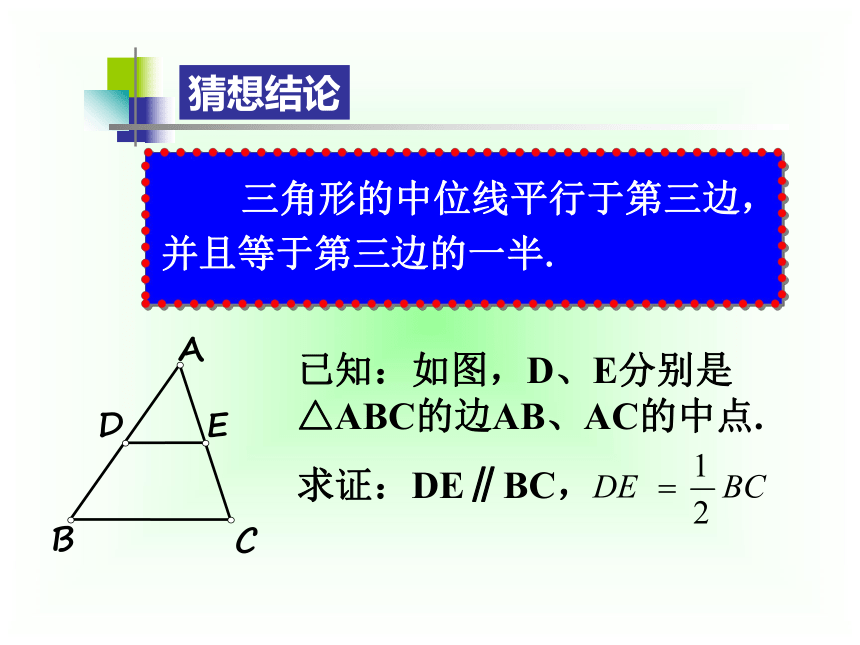
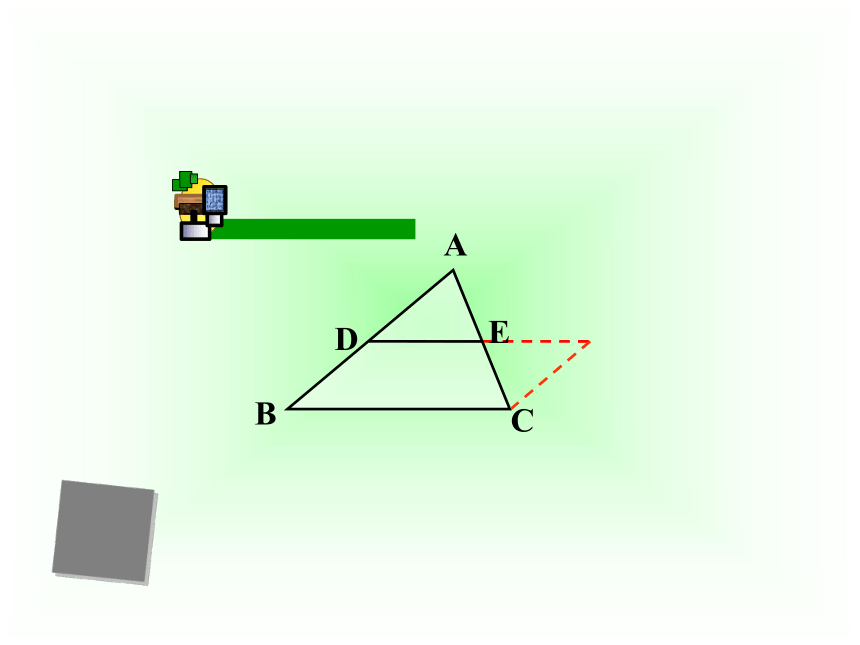
已知:如图,D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC,
C
E
D
B
A
猜想结论
温馨提示:与第三边的位置关系?与第三边的数量关系?
三角形的中位线平行于第三边,并且等于第三边的一半.
C
E
D
F
B
A
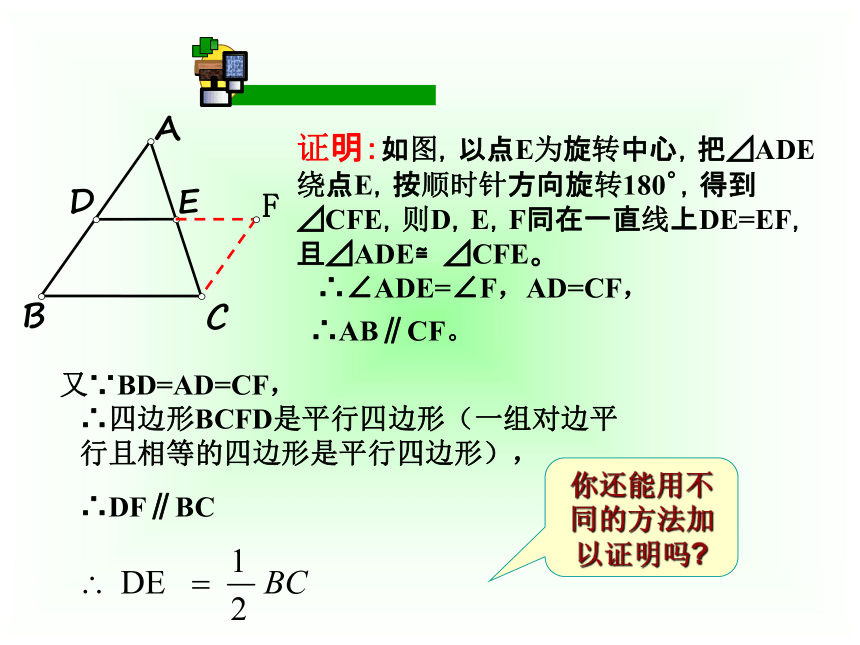
你还能用不同的方法加以证明吗?
证明:如图,以点E为旋转中心,把⊿ADE绕点E,按顺时针方向旋转180゜,得到⊿CFE,则D,E,F同在一直线上DE=EF,且⊿ADE≌⊿CFE。
∴∠ADE=∠F,AD=CF,
∴AB∥CF。
又∵BD=AD=CF,
∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴DF∥BC
方法1
C
E
D
F
A
方法2
B
A
B
C
D
E
方法3
方法4
F
B
C
E
D
A
三角形的中位线性质
如果
DE是△ABC的中位线
那么
⑴
DE∥BC,
⑵
DE=1/2BC
①
证明平行问题
②
证明一条线段是另一条线段的2倍或1/2
用
途
A
B
C
D
E
中点想到
中线、中位线
三角形的中位线平行于第三边,并且等于第三边的一半.
A
B
C
E
F
D
如图,已知△ABC,D、E、F分别是BC、AB、AC边上的中点。
(3)若△ABC的周长为18cm,它的三条中位线围成的△DEF的周长是______图中有_____个平行四边形
初显身手
(1)若∠AEF=60°,
则∠B=
度,为什么?(口答)
(2)若BC=8cm,
则EF=
cm,为什么?(口答)
60
4
9cm
3
(2007湖南怀化)如图:
分别是
的中点,
,
,
分别是
,
,
的中点这样延续下去.已知△ABC的周长是
1,
的周长是
,
的周长是
的周长是
,则
.
…^
A
B
C
课外拓展
(2009浙江)如图,DE是⊿ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.
F
E
D
C
B
A
O
分析
:连接DE、EF,根据中位线的定理证明四边形ADFE是平行四边形.
小试牛刀
已知:如图,在四边形ABCD中,E、F、G、
H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
分析
:
由E,F,G,H分别是四边形ABCD各边的中点,联想到应用三角形的中位线
定理来证明.
证明:
连结AC.
∵
EF是⊿ABC的一条中位线,
∴EF=
AC
EF//AC
(三角形的中位线平行于第三边,并且等于张三边的一半)
∴四边形EFGH是平行四边形
(一组对边平行并且相等的四边形是平行四边形).
∴
EF//HG
EF=HG
A
B
C
D
E
F
G
H
同理可证HG//AC
HG=
AC
方法1
证明:
连结AC
BD
∵
EF和HG分别是⊿ABC
和 ⊿ADC的中位线 ∴
EF//AC
HG//AC(三角形的中位线平行于第三 边,并且等于张三边的一半)
∴
EF//HG
同理可证
EH//FG
∴四边形EFGH是平行四边形
(两组对边分别平行的四边形是平行四边形).
A
B
C
D
E
F
G
H
方法2
谈谈收获
亲爱的同学们:
今天我们上了一节有关三角形中位线的课,在这节课上,我学会……
定义:连结三角形两边中点的线段叫做三角形的中位线。
性质:三角形的中位线平行于第三边,并且等于第三边的一半。
应用:
①
证明平行问题。②
证明一条线段是另一条线段的2倍或1/2
6.3
三角形的中位线
1、齐头并进
打一数学中的几何名词
(平行)
2、风筝跑了
(线段)
课前游戏
猜一猜
如图,有一块三角形的蛋糕,准备平均分给四个小朋友,要求四人所分的形状大小相同,请设计合理的解决方案。
F
(中点)
(中点)D
E(中点)
A
B
C
连结三角形两边中点的线段
叫三角形的中位线
三角形有三条中位线
因为D、E分别为AB、AC的中点
三角形的中位线和三角形的中线不同
同理DF、EF也为△ABC的中位线
E
D
F
A
C
B
所以
DE为
△
ABC的中位线
注意
获取新知
已知:如图,D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC,
C
E
D
B
A
猜想结论
温馨提示:与第三边的位置关系?与第三边的数量关系?
三角形的中位线平行于第三边,并且等于第三边的一半.
C
E
D
F
B
A
你还能用不同的方法加以证明吗?
证明:如图,以点E为旋转中心,把⊿ADE绕点E,按顺时针方向旋转180゜,得到⊿CFE,则D,E,F同在一直线上DE=EF,且⊿ADE≌⊿CFE。
∴∠ADE=∠F,AD=CF,
∴AB∥CF。
又∵BD=AD=CF,
∴四边形BCFD是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴DF∥BC
方法1
C
E
D
F
A
方法2
B
A
B
C
D
E
方法3
方法4
F
B
C
E
D
A
三角形的中位线性质
如果
DE是△ABC的中位线
那么
⑴
DE∥BC,
⑵
DE=1/2BC
①
证明平行问题
②
证明一条线段是另一条线段的2倍或1/2
用
途
A
B
C
D
E
中点想到
中线、中位线
三角形的中位线平行于第三边,并且等于第三边的一半.
A
B
C
E
F
D
如图,已知△ABC,D、E、F分别是BC、AB、AC边上的中点。
(3)若△ABC的周长为18cm,它的三条中位线围成的△DEF的周长是______图中有_____个平行四边形
初显身手
(1)若∠AEF=60°,
则∠B=
度,为什么?(口答)
(2)若BC=8cm,
则EF=
cm,为什么?(口答)
60
4
9cm
3
(2007湖南怀化)如图:
分别是
的中点,
,
,
分别是
,
,
的中点这样延续下去.已知△ABC的周长是
1,
的周长是
,
的周长是
的周长是
,则
.
…^
A
B
C
课外拓展
(2009浙江)如图,DE是⊿ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.
F
E
D
C
B
A
O
分析
:连接DE、EF,根据中位线的定理证明四边形ADFE是平行四边形.
小试牛刀
已知:如图,在四边形ABCD中,E、F、G、
H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
A
B
C
D
E
F
G
H
分析
:
由E,F,G,H分别是四边形ABCD各边的中点,联想到应用三角形的中位线
定理来证明.
证明:
连结AC.
∵
EF是⊿ABC的一条中位线,
∴EF=
AC
EF//AC
(三角形的中位线平行于第三边,并且等于张三边的一半)
∴四边形EFGH是平行四边形
(一组对边平行并且相等的四边形是平行四边形).
∴
EF//HG
EF=HG
A
B
C
D
E
F
G
H
同理可证HG//AC
HG=
AC
方法1
证明:
连结AC
BD
∵
EF和HG分别是⊿ABC
和 ⊿ADC的中位线 ∴
EF//AC
HG//AC(三角形的中位线平行于第三 边,并且等于张三边的一半)
∴
EF//HG
同理可证
EH//FG
∴四边形EFGH是平行四边形
(两组对边分别平行的四边形是平行四边形).
A
B
C
D
E
F
G
H
方法2
谈谈收获
亲爱的同学们:
今天我们上了一节有关三角形中位线的课,在这节课上,我学会……
定义:连结三角形两边中点的线段叫做三角形的中位线。
性质:三角形的中位线平行于第三边,并且等于第三边的一半。
应用:
①
证明平行问题。②
证明一条线段是另一条线段的2倍或1/2
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
