《第11章反比例函数》期末综合复习能力提升训练1-2020-2021学年苏科版八年级数学下册(Word版 附答案)
文档属性
| 名称 | 《第11章反比例函数》期末综合复习能力提升训练1-2020-2021学年苏科版八年级数学下册(Word版 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 413.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 00:00:00 | ||
图片预览


文档简介
2021苏科版八年级数学下册《第11章反比例函数》期末综合复习能力提升训练1(附答案)
1.一次函数y=k(x+1)与函数y=在同一坐标系中的图象可能是( )
A.B.C.D.
2.若点A(x1,﹣5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x2<x3<x1 B.x1<x3<x2 C.x1<x2<x3 D.x3<x1<x2
3.已知反比例函数y=(k为常数)与正比例函数y=x的图象有交点,k的取值范围是( )
A.k>0 B.k<0 C.k>3 D.k<3
4.如图,点(3,k)在双曲线y=上,过点A作AC⊥x轴,垂足为C,线段OA的垂平分线交OC于点B,则△ABC周长的值是( )
A.3 B.2+ C.4 D.3+
5.如图,在平面直角坐标系中,正方形ABCO绕点O顺时针旋转,反比例函数y=﹣的图象经过点B,当点A的坐标为(﹣3,1)时,k的值为( )
A.﹣8 B.﹣6 C.﹣4 D.﹣3
6.已知反比例函数y=﹣,当﹣3<x<﹣1时,y的取值范围是( )
A.﹣3<y<﹣1 B.y>﹣3 C.1<y<3 D.y>﹣1
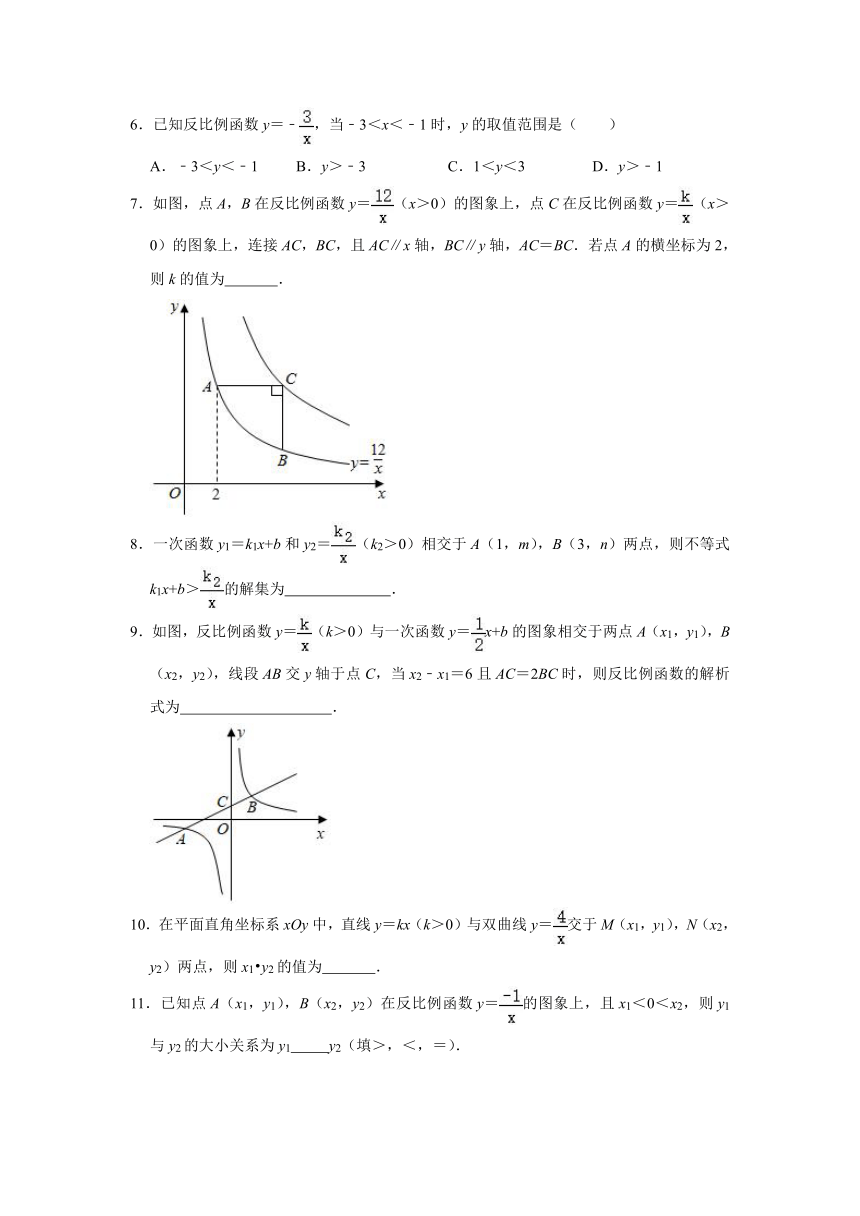
7.如图,点A,B在反比例函数y=(x>0)的图象上,点C在反比例函数y=(x>0)的图象上,连接AC,BC,且AC∥x轴,BC∥y轴,AC=BC.若点A的横坐标为2,则k的值为 .
8.一次函数y1=k1x+b和y2=(k2>0)相交于A(1,m),B(3,n)两点,则不等式k1x+b>的解集为 .
9.如图,反比例函数y=(k>0)与一次函数y=x+b的图象相交于两点A(x1,y1),B(x2,y2),线段AB交y轴于点C,当x2﹣x1=6且AC=2BC时,则反比例函数的解析式为 .
10.在平面直角坐标系xOy中,直线y=kx(k>0)与双曲线y=交于M(x1,y1),N(x2,y2)两点,则x1?y2的值为 .
11.已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则y1与y2的大小关系为y1 y2(填>,<,=).
12.如图,A,B是双曲线y=kx﹣1上的两点,过A点作AC⊥x轴,交OB于点D,垂足为C.若△ADO的面积为3,D为OB的中点,则k的值为 .
13.如图,正方形ABOC与正方形EFCD的边OC、CD均在x轴上,点F在AC边上,反比例函数y=的图象经过点A、E,且S△OAE=5,则k= .
14.如图,?ABCD的顶点A、B在x轴上,顶点D在y轴上,顶点C在第一象限,反比例函数y=(x>0)的分支过点C,若?ABCD的面积为3,则k= .
15.如图,在第二象限的双曲线y=﹣上有一点A,过A作AB∥x轴交第二象限的另一条双曲线y=﹣于点B,连接OA,OB,则△AOB的面积为 .
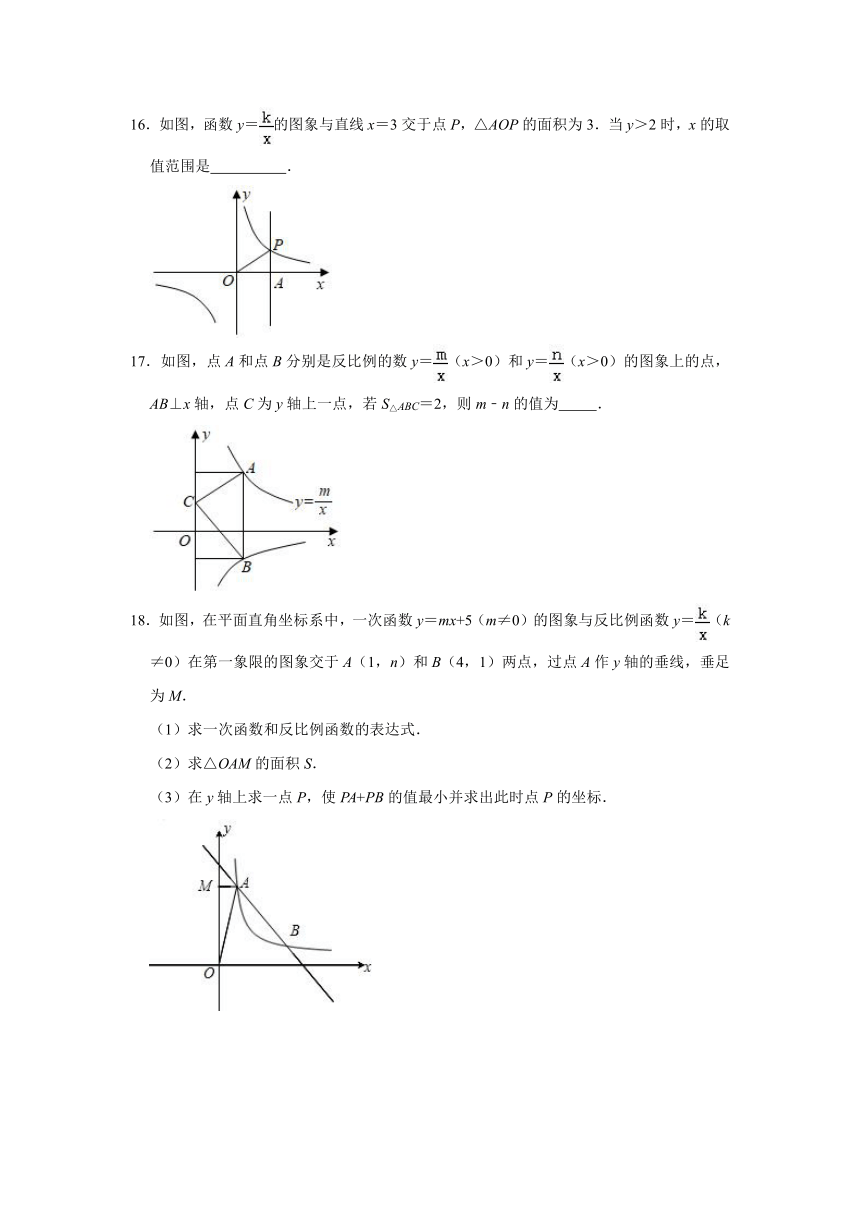
16.如图,函数y=的图象与直线x=3交于点P,△AOP的面积为3.当y>2时,x的取值范围是 .
17.如图,点A和点B分别是反比例的数y=(x>0)和y=(x>0)的图象上的点,AB⊥x轴,点C为y轴上一点,若S△ABC=2,则m﹣n的值为 .
18.如图,在平面直角坐标系中,一次函数y=mx+5(m≠0)的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的表达式.
(2)求△OAM的面积S.
(3)在y轴上求一点P,使PA+PB的值最小并求出此时点P的坐标.
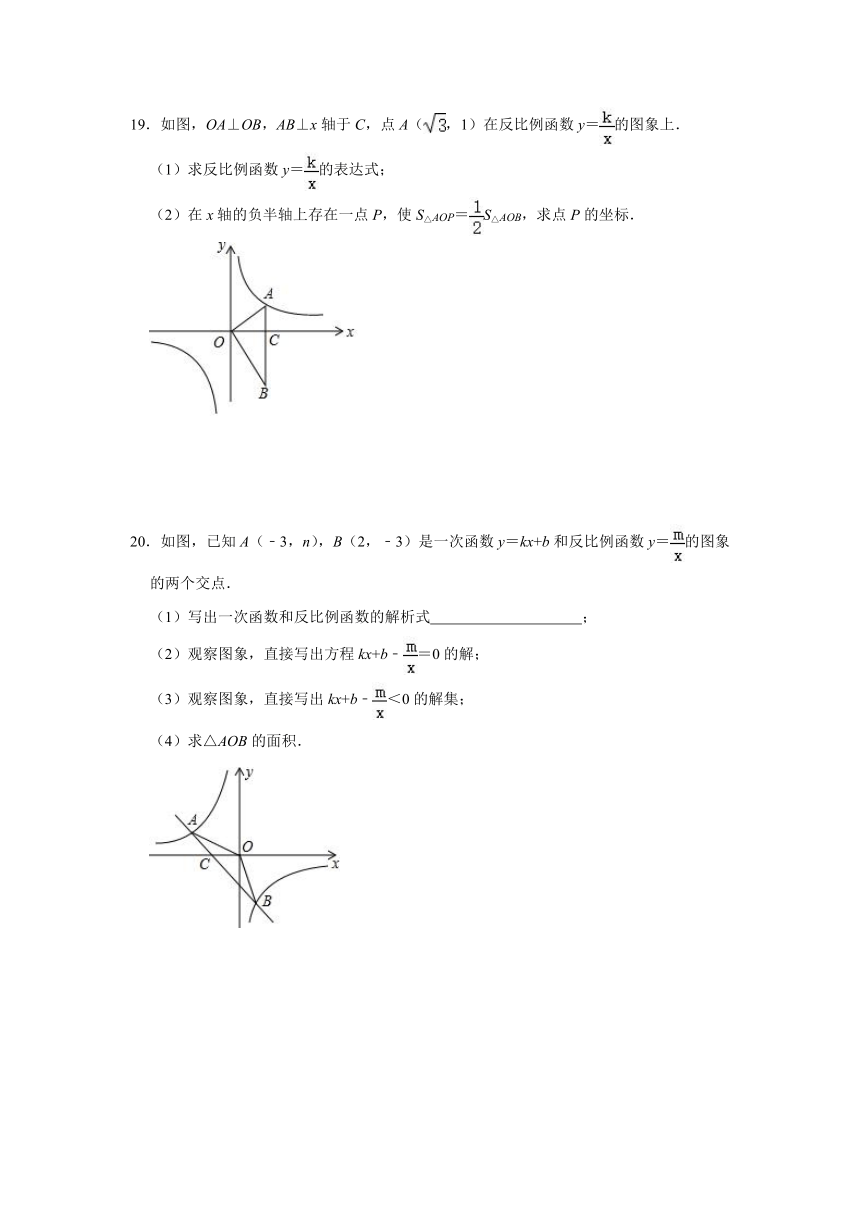
19.如图,OA⊥OB,AB⊥x轴于C,点A(,1)在反比例函数y=的图象上.
(1)求反比例函数y=的表达式;
(2)在x轴的负半轴上存在一点P,使S△AOP=S△AOB,求点P的坐标.
20.如图,已知A(﹣3,n),B(2,﹣3)是一次函数y=kx+b和反比例函数y=的图象的两个交点.
(1)写出一次函数和反比例函数的解析式 ;
(2)观察图象,直接写出方程kx+b﹣=0的解;
(3)观察图象,直接写出kx+b﹣<0的解集;
(4)求△AOB的面积.
21.如图,一次函数y=k1x+b与反比例函数y=(x>0)的图象交于A(1,6),B(3,n)两点.
(1)求反比例函数的解析式和n的值;
(2)根据图象直接写出不等式k1x+b的x的取值范围;
(3)求△AOB的面积.
22.如图,点A,点C分别为双曲线y=上位于第一,第三象限分支上的点,过点A作AB⊥x轴于点B,△AOB的面积为1,OB=2,点C(﹣1,n).
(1)求n的值;
(2)若以O,A,C,D四点为顶点的四边形为平行四边形,请直接写出所有满足条件的点D的坐标.
23.如图,在平面直角坐标系中,O为坐标原点,经过原点的直线l与反比例函数y=(x>0)的图象交于点C,B是直线l上的点,过点B作BA⊥x轴,垂足为点A,且C是OB中点,已知OA=4,BD=3.
(1)用含k的代数式来表示D点的坐标为 ;
(2)求反比例函数的解析式;
(3)连接CD,求四边形OADC的面积.
24.如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都在坐标轴上,点B的坐标是(4,2),反比例函数y=与AB,BC分别交于点D,E.
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标.
25.如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求经过点E的反比例函数解析式和直线BE的解析式.
26.已知点A,B在反比例函数y=(x>0)的图象上,且横坐标分别为m,n,过点A向y轴作垂线段,过点B向x轴作垂线段,两条垂线段交于点C,过点A,B分别作AD⊥x轴于D,BE⊥y轴于E.
(1)若m=6,n=1,求点C的坐标;
(2)若m(n﹣2)=3,当点C在直线DE上时,求n的值.
参考答案
1.解:k>0时,一次函数y=k(x+1)的图象经过第一、二、三象限,
反比例函数的两个分支分别位于第一、三象限,选项B符合;
k<0时,一次函数y=k(x+1)的图象经过第二、三、四象限,
反比例函数的两个分支分别位于第二、四象限,无选项符合.
故选:B.
2.∵点A(x1,﹣5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,
∴x1=,x2=1,,
∴x1<x3<x2,
故选:B.
3.解:由正比例函数y=x可知直线过一、三象限,
∵反比例函数y=(k为常数)与正比例函数y=x的图象有交点,
∴反比例函数y=(k为常数)位于一、三象限,
∴k﹣3>0,
∴k>3,
故选:C.
4.解:∵点(3,k)在双曲线y=上,
∴k=1,
∴A(3,1),
∴OC=3,AC=1.
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=AB+BC+AC=OB+BC+AC=OC+AC=3+1=4.
故选:C.
5.解:作AD⊥x轴于D,CE⊥x轴于E,
∵点A的坐标为(﹣3,1),
∴OD=3,AD=1,
∵∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
,
∴△AOD≌△OCE(AAS),
∴AD=OE=1,OD=CE=3,
∴C(1,3),
∴正方形的中心点Q(﹣1,2),
∴B(﹣2,4),
∵反比例函数y=﹣的图象经过点B,
∴k=﹣2×4=﹣8,
故选:A.
6.解:∵反比例函数y=﹣中k=﹣3<0,
∴反比例函数图象在二、四象限,且在每个象限y随x的增大而增大,
∴当﹣3<x<﹣1时,y的取值范围为1<y<3,
故选:C.
7.解:当x=2时,y==6,则A(2,6),
∵AC∥x轴,
∴C点的纵坐标为6,
设C(,6),
∵BC∥y轴,
∴B点的横坐标为,
∴B(,),
∵CA=CB,
∴﹣2=6﹣,
整理得k2﹣48k+432=0,解得k1=36,k2=12,
经检验k1=36,k2=12都为原方程的解,
∴k=36.
故答案为36.
8.解:如图,由图象可得:不等式k1x+b>的解集为是1<x<3或x<0.
故答案为:1<x<3或x<0.
9.解:∵AC=2BC,
∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.
∵点A、点B都在一次函数y=x+b的图象上,
∴可设B(m,m+b),则A(﹣2m,﹣m+b).
∵x2﹣x1=6,
∴m﹣(﹣2m)=6,
∴m=2.
∴B(2,1+b),则A(﹣4,﹣2+b).
又∵点A、点B都在反比例函数y=(k>0)的图象上,
∴2(1+b)=﹣4(﹣2+b),
∴b=1;
∴B(2,2),
∴k=2×2=4,
∴反比例函数的解析式为y=.
故答案为y=.
10.解:联立两个函数表达式得:kx=,即kx2﹣4=0,
则x1x2=﹣,
点N在直线上,则y2=kx2,
故x1?y2=kx1x2=k(﹣)=﹣4,
故答案为﹣4.
11.解:∵k=﹣1<0,
∴双曲线在第二,四象限,
∵x1<0<x2,
∴A在第二象限,B在第四象限,
∴y1>y2;
故答案为>.
12.解:过点B作BE⊥x轴于点E,
∵D为OB的中点,CD∥BE,
∴CD是△OBE的中位线,即CD=BE.
设A(x,),则B(2x,),CD=,AD=﹣,
∵△ADO的面积为3,
∴AD?OC=3,
∴(﹣)?x=3,
解得k=8,
故答案是:8.
13.解:∵四边形ABOC和EFCD均为正方形,
∴OC=AC,ED=CD,
设A点坐标为(m,m),E点坐标为(m+n,n),
∵A、E在反比例函数y=上,
∴m2=k,(m+n)n=k,
∴S△OAC=OC?CA==,
∴S四边形ACDE=CD(AC+DE)=n(m+n)=,
∴S△ODE=OD?DE=(m+n)n=,
又∵S△OAE=S△OAC+S四边形ACDE﹣S△ODE=5,
∴+﹣=5,
∴k=10,
故答案为:10.
14.解:如图,过点C作CE⊥AB于E,连接OC,
∵?ABCD的面积为3,
∴AB?CE=3.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠DAO=∠CBA.
∵DO⊥AO,CE⊥AB,
∴∠DOA=∠CEB=90°.
∴△DOA≌△CEB(AAS).
∴S△ODA=S△CEB.
∴S矩形DOEC=S平行四边形ABCD=3.
∴OE?CE=3.
设C(a,b),
∵C在第一象限,
∴a>0,b>0.
∴OE=a,CE=b.
∴OE?CE=ab=3.
∴k=ab=3.
故答案为:3.
15.解:延长AB交y轴于C,
∵AB∥x轴,
∴S△ABO=S△ABC﹣S△BOC=﹣=10.
故答案为:10.
16.解:∵△AOP的面积为3,
∴k=2×3=6.
把x=3代入y=得y=2,
∴0<x<3时y>2.
故答案为:0<x<3.
17.解:连接AO.CO,
∵AB⊥x轴,点C为y轴上一点,
∴AB∥y轴,
∴S△ABC=S△ABO=2,
∴=2.
∴=2,
即m﹣n=4.
故答案为:4.
18.解:(1)将B(4,1)代入y=得:.
∴k=4.
∴y=.
将B(4,1)代入y=mx+5得:1=4m+5,
∴m=﹣1.
∴y=﹣x+5.
(2)在y=中,令x=1,解得y=4.
∴A(1,4).
∴S=×1×4=2.
(3)作点A关于y轴的对称点N,则N(﹣1,4).
连接BN交y轴于点P,点P即为所求.
设直线BN的关系式为y=kx+b,
由,得,
∴y=﹣x+.
∴点P的坐标为(0,).
19.解:(1)把A(,1)代入反比例函数y=得:k=1×=,
所以反比例函数的表达式为y=;
(2)∵A(,1),OA⊥AB,AB⊥x轴于C,
∴OC=,AC=1,
OA===2,
∵tanA==,
∴∠A=60°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠B=30°,
∴OB=2OC=2,
∴S△AOB===2,
∵S△AOP=S△AOB,
∴,
∵AC=1,
∴OP=2,
∴点P的坐标为(﹣2,0).
20.解:(1)B(2,﹣3)都在反比例函数y=的图象上,
∴m=2×(﹣3)=﹣6,
则反比例函数的解析式是y=﹣,
当x=﹣3时,y=n=2,
则A的坐标是(﹣3,2).
根据题意得,
解得:,
则一次函数的解析式是y=﹣x﹣1.
故答案是:y=﹣x﹣1,y=﹣;
(2)根据题意得方程kx+b﹣=0的解是x=﹣3或2;
(3)kx+b﹣<0的解集是:﹣3<x<0或x>2;
(4)在y=﹣x﹣1中,令y=0,解得x=﹣1,
则C的坐标是(﹣1,0)
S△AOC=×1×2=1,S△BOC=×1×3=,
S△AOB=S△AOC+S△BOC=1+=.
21.解:(1)∵A(1,6),B(3,n)在y=的图象上,
∴k2=6,
∴反比例函数的解析式是y=.
∴n==2;
(2)当0<x<1或x>3时,k1x+b<;
(3)∵A(1,6),B(3,2)在函数y=k1x+b的图象上,
∴,
解得:,
则一次函数的解析式是y=﹣2x+8,
设直线y=﹣2x+8与x轴相交于点C,C的坐标是(4,0).
S△AOB=S△AOC﹣S△BOC=OC|yA|﹣OC|yB)=8.
22.解:(1)∵过点A作AB⊥x轴于点B,△AOB的面积为1,
∴S△AOB=|k|=1,
∴|k|=2,
∵在一三象限,
∴k=2,
∴反比例函数为y=,
把(﹣1,n)代入得,n=﹣2;
(2)∵OB=2,S△AOB=1,
∴AB=1,
∴A(2,1),
如图,A(2,1),O(0,0),C(﹣1,﹣2),
设D(x,y),
①以AC为对角线时,可得OA=CD,OA∥CD,
于是有﹣1﹣x=﹣2,﹣2﹣y=﹣1,
解得x=1,y=﹣1,
∴D(1,﹣1);
②以OA 为对角线时,可得CO∥AD,CO=AD,
于是有2﹣x=﹣1,1﹣y=﹣2,
解得x=3,y=3,
∴D(3,3);
③以OC为对角线时,可得OA∥CD,OA=CD,
于是有x+1=﹣2,y+2=﹣1,
解得x=﹣3,y=﹣3,
∴D(﹣3,﹣3);
综上所述,符合条件的点D有3个,其坐标分别为(1,﹣1)、(3,3)、(﹣3,﹣3).
23.解:(1)∵OA=4,
∴D(4,),
故答案为(4,).
(2)由(1)可知,B(4,+3),
∵OC=CB,
∴C(2,+),
∵点C在y=上,
∴2×(+)=k,
解得k=4,
∴反比例函数的解析式为y=.
(3)连接CD、AC.
∵C(2,2),D(4,1),
∴S△OADC=S△AOC+S△ADC=×4×2+×1×2=5.
24.解:(1)由B(4,2)知,点D的横坐标是4,点E的纵坐标是2,
又∵点D,E都在y=的图象上.
∴D(4,1),E(2,2).(2分)
设直线DE的解析式为y+kx+b,把D(4,1),E(2,2)代入,得
解得,
∴直线DE的解析式为y=﹣x+3.
(2)∵D(4,1),E(2,2),B(4,2),
∴S△ODE=S矩形OABC﹣S△OCE﹣S△BDE﹣S△OAD
=2×4﹣×2×2﹣×1×2﹣×1×4
=3.
∵点F为y轴上一点,S△OEF=S△ODE,
∴S△OEF=×OF×2=3.
∴OF=3.
∴F的坐标为(0,3)或(0,﹣3).
25.(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA=AC,DB=OB,AC=OB,
∴DA=DB,
∴四边形AEBD是菱形;
(2)解:连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF=OA=,AF=AB=1,3+=,
∴点E坐标为:(,1),
设经过点E的反比例函数解析式为:y=,
把点E代入得:k=,
∴经过点E的反比例函数解析式为:y=.
∵四边形OABC是矩形,OA=3,OC=2,
∴B(3,2).
设直线BE的解析式为y=mx+n,将B、E两点的坐标代入,
得,解得,
∴直线BE的解析式为y=﹣x+4.
26.解:(1)∵m=6时,y==1,
∴A(6,1).
∵n=1时,y==6,
∴B(1,6).
∵过点A向y轴作垂线段,过点B向x轴作垂线段,两条垂线段交于点C,
∴C(1,1);
(2)如图.
∵点A,B在反比例函数y=(x>0)的图象上,且横坐标分别为m,n,
∴A(m,),B(n,)(m>0,n>0),
∴D(m,0),E(0,),C(n,).
设直线DE的解析式为y=kx+b,
则,解得,
∴直线DE的解析式为y=﹣x+.
∵点C在直线DE上,
∴=﹣×n+,
化简得m=2n.
把m=2n代入m(n﹣2)=3,整理,得2n2﹣4n﹣3=0,
解得n=,
∵n>0,
∴n=.
1.一次函数y=k(x+1)与函数y=在同一坐标系中的图象可能是( )
A.B.C.D.
2.若点A(x1,﹣5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A.x2<x3<x1 B.x1<x3<x2 C.x1<x2<x3 D.x3<x1<x2
3.已知反比例函数y=(k为常数)与正比例函数y=x的图象有交点,k的取值范围是( )
A.k>0 B.k<0 C.k>3 D.k<3
4.如图,点(3,k)在双曲线y=上,过点A作AC⊥x轴,垂足为C,线段OA的垂平分线交OC于点B,则△ABC周长的值是( )
A.3 B.2+ C.4 D.3+
5.如图,在平面直角坐标系中,正方形ABCO绕点O顺时针旋转,反比例函数y=﹣的图象经过点B,当点A的坐标为(﹣3,1)时,k的值为( )
A.﹣8 B.﹣6 C.﹣4 D.﹣3
6.已知反比例函数y=﹣,当﹣3<x<﹣1时,y的取值范围是( )
A.﹣3<y<﹣1 B.y>﹣3 C.1<y<3 D.y>﹣1
7.如图,点A,B在反比例函数y=(x>0)的图象上,点C在反比例函数y=(x>0)的图象上,连接AC,BC,且AC∥x轴,BC∥y轴,AC=BC.若点A的横坐标为2,则k的值为 .
8.一次函数y1=k1x+b和y2=(k2>0)相交于A(1,m),B(3,n)两点,则不等式k1x+b>的解集为 .
9.如图,反比例函数y=(k>0)与一次函数y=x+b的图象相交于两点A(x1,y1),B(x2,y2),线段AB交y轴于点C,当x2﹣x1=6且AC=2BC时,则反比例函数的解析式为 .
10.在平面直角坐标系xOy中,直线y=kx(k>0)与双曲线y=交于M(x1,y1),N(x2,y2)两点,则x1?y2的值为 .
11.已知点A(x1,y1),B(x2,y2)在反比例函数y=的图象上,且x1<0<x2,则y1与y2的大小关系为y1 y2(填>,<,=).
12.如图,A,B是双曲线y=kx﹣1上的两点,过A点作AC⊥x轴,交OB于点D,垂足为C.若△ADO的面积为3,D为OB的中点,则k的值为 .
13.如图,正方形ABOC与正方形EFCD的边OC、CD均在x轴上,点F在AC边上,反比例函数y=的图象经过点A、E,且S△OAE=5,则k= .
14.如图,?ABCD的顶点A、B在x轴上,顶点D在y轴上,顶点C在第一象限,反比例函数y=(x>0)的分支过点C,若?ABCD的面积为3,则k= .
15.如图,在第二象限的双曲线y=﹣上有一点A,过A作AB∥x轴交第二象限的另一条双曲线y=﹣于点B,连接OA,OB,则△AOB的面积为 .
16.如图,函数y=的图象与直线x=3交于点P,△AOP的面积为3.当y>2时,x的取值范围是 .
17.如图,点A和点B分别是反比例的数y=(x>0)和y=(x>0)的图象上的点,AB⊥x轴,点C为y轴上一点,若S△ABC=2,则m﹣n的值为 .
18.如图,在平面直角坐标系中,一次函数y=mx+5(m≠0)的图象与反比例函数y=(k≠0)在第一象限的图象交于A(1,n)和B(4,1)两点,过点A作y轴的垂线,垂足为M.
(1)求一次函数和反比例函数的表达式.
(2)求△OAM的面积S.
(3)在y轴上求一点P,使PA+PB的值最小并求出此时点P的坐标.
19.如图,OA⊥OB,AB⊥x轴于C,点A(,1)在反比例函数y=的图象上.
(1)求反比例函数y=的表达式;
(2)在x轴的负半轴上存在一点P,使S△AOP=S△AOB,求点P的坐标.
20.如图,已知A(﹣3,n),B(2,﹣3)是一次函数y=kx+b和反比例函数y=的图象的两个交点.
(1)写出一次函数和反比例函数的解析式 ;
(2)观察图象,直接写出方程kx+b﹣=0的解;
(3)观察图象,直接写出kx+b﹣<0的解集;
(4)求△AOB的面积.
21.如图,一次函数y=k1x+b与反比例函数y=(x>0)的图象交于A(1,6),B(3,n)两点.
(1)求反比例函数的解析式和n的值;
(2)根据图象直接写出不等式k1x+b的x的取值范围;
(3)求△AOB的面积.
22.如图,点A,点C分别为双曲线y=上位于第一,第三象限分支上的点,过点A作AB⊥x轴于点B,△AOB的面积为1,OB=2,点C(﹣1,n).
(1)求n的值;
(2)若以O,A,C,D四点为顶点的四边形为平行四边形,请直接写出所有满足条件的点D的坐标.
23.如图,在平面直角坐标系中,O为坐标原点,经过原点的直线l与反比例函数y=(x>0)的图象交于点C,B是直线l上的点,过点B作BA⊥x轴,垂足为点A,且C是OB中点,已知OA=4,BD=3.
(1)用含k的代数式来表示D点的坐标为 ;
(2)求反比例函数的解析式;
(3)连接CD,求四边形OADC的面积.
24.如图,在平面直角坐标系中,原点O是矩形OABC的一个顶点,点A、C都在坐标轴上,点B的坐标是(4,2),反比例函数y=与AB,BC分别交于点D,E.
(1)求直线DE的解析式;
(2)若点F为y轴上一点,△OEF和△ODE的面积相等,求点F的坐标.
25.如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB.
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求经过点E的反比例函数解析式和直线BE的解析式.
26.已知点A,B在反比例函数y=(x>0)的图象上,且横坐标分别为m,n,过点A向y轴作垂线段,过点B向x轴作垂线段,两条垂线段交于点C,过点A,B分别作AD⊥x轴于D,BE⊥y轴于E.
(1)若m=6,n=1,求点C的坐标;
(2)若m(n﹣2)=3,当点C在直线DE上时,求n的值.
参考答案
1.解:k>0时,一次函数y=k(x+1)的图象经过第一、二、三象限,
反比例函数的两个分支分别位于第一、三象限,选项B符合;
k<0时,一次函数y=k(x+1)的图象经过第二、三、四象限,
反比例函数的两个分支分别位于第二、四象限,无选项符合.
故选:B.
2.∵点A(x1,﹣5),B(x2,2),C(x3,5)都在反比例函数y=的图象上,
∴x1=,x2=1,,
∴x1<x3<x2,
故选:B.
3.解:由正比例函数y=x可知直线过一、三象限,
∵反比例函数y=(k为常数)与正比例函数y=x的图象有交点,
∴反比例函数y=(k为常数)位于一、三象限,
∴k﹣3>0,
∴k>3,
故选:C.
4.解:∵点(3,k)在双曲线y=上,
∴k=1,
∴A(3,1),
∴OC=3,AC=1.
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=AB+BC+AC=OB+BC+AC=OC+AC=3+1=4.
故选:C.
5.解:作AD⊥x轴于D,CE⊥x轴于E,
∵点A的坐标为(﹣3,1),
∴OD=3,AD=1,
∵∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠OAD=∠COE,
在△AOD和△OCE中,
,
∴△AOD≌△OCE(AAS),
∴AD=OE=1,OD=CE=3,
∴C(1,3),
∴正方形的中心点Q(﹣1,2),
∴B(﹣2,4),
∵反比例函数y=﹣的图象经过点B,
∴k=﹣2×4=﹣8,
故选:A.
6.解:∵反比例函数y=﹣中k=﹣3<0,
∴反比例函数图象在二、四象限,且在每个象限y随x的增大而增大,
∴当﹣3<x<﹣1时,y的取值范围为1<y<3,
故选:C.
7.解:当x=2时,y==6,则A(2,6),
∵AC∥x轴,
∴C点的纵坐标为6,
设C(,6),
∵BC∥y轴,
∴B点的横坐标为,
∴B(,),
∵CA=CB,
∴﹣2=6﹣,
整理得k2﹣48k+432=0,解得k1=36,k2=12,
经检验k1=36,k2=12都为原方程的解,
∴k=36.
故答案为36.
8.解:如图,由图象可得:不等式k1x+b>的解集为是1<x<3或x<0.
故答案为:1<x<3或x<0.
9.解:∵AC=2BC,
∴A点的横坐标的绝对值是B点横坐标绝对值的两倍.
∵点A、点B都在一次函数y=x+b的图象上,
∴可设B(m,m+b),则A(﹣2m,﹣m+b).
∵x2﹣x1=6,
∴m﹣(﹣2m)=6,
∴m=2.
∴B(2,1+b),则A(﹣4,﹣2+b).
又∵点A、点B都在反比例函数y=(k>0)的图象上,
∴2(1+b)=﹣4(﹣2+b),
∴b=1;
∴B(2,2),
∴k=2×2=4,
∴反比例函数的解析式为y=.
故答案为y=.
10.解:联立两个函数表达式得:kx=,即kx2﹣4=0,
则x1x2=﹣,
点N在直线上,则y2=kx2,
故x1?y2=kx1x2=k(﹣)=﹣4,
故答案为﹣4.
11.解:∵k=﹣1<0,
∴双曲线在第二,四象限,
∵x1<0<x2,
∴A在第二象限,B在第四象限,
∴y1>y2;
故答案为>.
12.解:过点B作BE⊥x轴于点E,
∵D为OB的中点,CD∥BE,
∴CD是△OBE的中位线,即CD=BE.
设A(x,),则B(2x,),CD=,AD=﹣,
∵△ADO的面积为3,
∴AD?OC=3,
∴(﹣)?x=3,
解得k=8,
故答案是:8.
13.解:∵四边形ABOC和EFCD均为正方形,
∴OC=AC,ED=CD,
设A点坐标为(m,m),E点坐标为(m+n,n),
∵A、E在反比例函数y=上,
∴m2=k,(m+n)n=k,
∴S△OAC=OC?CA==,
∴S四边形ACDE=CD(AC+DE)=n(m+n)=,
∴S△ODE=OD?DE=(m+n)n=,
又∵S△OAE=S△OAC+S四边形ACDE﹣S△ODE=5,
∴+﹣=5,
∴k=10,
故答案为:10.
14.解:如图,过点C作CE⊥AB于E,连接OC,
∵?ABCD的面积为3,
∴AB?CE=3.
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC.
∴∠DAO=∠CBA.
∵DO⊥AO,CE⊥AB,
∴∠DOA=∠CEB=90°.
∴△DOA≌△CEB(AAS).
∴S△ODA=S△CEB.
∴S矩形DOEC=S平行四边形ABCD=3.
∴OE?CE=3.
设C(a,b),
∵C在第一象限,
∴a>0,b>0.
∴OE=a,CE=b.
∴OE?CE=ab=3.
∴k=ab=3.
故答案为:3.
15.解:延长AB交y轴于C,
∵AB∥x轴,
∴S△ABO=S△ABC﹣S△BOC=﹣=10.
故答案为:10.
16.解:∵△AOP的面积为3,
∴k=2×3=6.
把x=3代入y=得y=2,
∴0<x<3时y>2.
故答案为:0<x<3.
17.解:连接AO.CO,
∵AB⊥x轴,点C为y轴上一点,
∴AB∥y轴,
∴S△ABC=S△ABO=2,
∴=2.
∴=2,
即m﹣n=4.
故答案为:4.
18.解:(1)将B(4,1)代入y=得:.
∴k=4.
∴y=.
将B(4,1)代入y=mx+5得:1=4m+5,
∴m=﹣1.
∴y=﹣x+5.
(2)在y=中,令x=1,解得y=4.
∴A(1,4).
∴S=×1×4=2.
(3)作点A关于y轴的对称点N,则N(﹣1,4).
连接BN交y轴于点P,点P即为所求.
设直线BN的关系式为y=kx+b,
由,得,
∴y=﹣x+.
∴点P的坐标为(0,).
19.解:(1)把A(,1)代入反比例函数y=得:k=1×=,
所以反比例函数的表达式为y=;
(2)∵A(,1),OA⊥AB,AB⊥x轴于C,
∴OC=,AC=1,
OA===2,
∵tanA==,
∴∠A=60°,
∵OA⊥OB,
∴∠AOB=90°,
∴∠B=30°,
∴OB=2OC=2,
∴S△AOB===2,
∵S△AOP=S△AOB,
∴,
∵AC=1,
∴OP=2,
∴点P的坐标为(﹣2,0).
20.解:(1)B(2,﹣3)都在反比例函数y=的图象上,
∴m=2×(﹣3)=﹣6,
则反比例函数的解析式是y=﹣,
当x=﹣3时,y=n=2,
则A的坐标是(﹣3,2).
根据题意得,
解得:,
则一次函数的解析式是y=﹣x﹣1.
故答案是:y=﹣x﹣1,y=﹣;
(2)根据题意得方程kx+b﹣=0的解是x=﹣3或2;
(3)kx+b﹣<0的解集是:﹣3<x<0或x>2;
(4)在y=﹣x﹣1中,令y=0,解得x=﹣1,
则C的坐标是(﹣1,0)
S△AOC=×1×2=1,S△BOC=×1×3=,
S△AOB=S△AOC+S△BOC=1+=.
21.解:(1)∵A(1,6),B(3,n)在y=的图象上,
∴k2=6,
∴反比例函数的解析式是y=.
∴n==2;
(2)当0<x<1或x>3时,k1x+b<;
(3)∵A(1,6),B(3,2)在函数y=k1x+b的图象上,
∴,
解得:,
则一次函数的解析式是y=﹣2x+8,
设直线y=﹣2x+8与x轴相交于点C,C的坐标是(4,0).
S△AOB=S△AOC﹣S△BOC=OC|yA|﹣OC|yB)=8.
22.解:(1)∵过点A作AB⊥x轴于点B,△AOB的面积为1,
∴S△AOB=|k|=1,
∴|k|=2,
∵在一三象限,
∴k=2,
∴反比例函数为y=,
把(﹣1,n)代入得,n=﹣2;
(2)∵OB=2,S△AOB=1,
∴AB=1,
∴A(2,1),
如图,A(2,1),O(0,0),C(﹣1,﹣2),
设D(x,y),
①以AC为对角线时,可得OA=CD,OA∥CD,
于是有﹣1﹣x=﹣2,﹣2﹣y=﹣1,
解得x=1,y=﹣1,
∴D(1,﹣1);
②以OA 为对角线时,可得CO∥AD,CO=AD,
于是有2﹣x=﹣1,1﹣y=﹣2,
解得x=3,y=3,
∴D(3,3);
③以OC为对角线时,可得OA∥CD,OA=CD,
于是有x+1=﹣2,y+2=﹣1,
解得x=﹣3,y=﹣3,
∴D(﹣3,﹣3);
综上所述,符合条件的点D有3个,其坐标分别为(1,﹣1)、(3,3)、(﹣3,﹣3).
23.解:(1)∵OA=4,
∴D(4,),
故答案为(4,).
(2)由(1)可知,B(4,+3),
∵OC=CB,
∴C(2,+),
∵点C在y=上,
∴2×(+)=k,
解得k=4,
∴反比例函数的解析式为y=.
(3)连接CD、AC.
∵C(2,2),D(4,1),
∴S△OADC=S△AOC+S△ADC=×4×2+×1×2=5.
24.解:(1)由B(4,2)知,点D的横坐标是4,点E的纵坐标是2,
又∵点D,E都在y=的图象上.
∴D(4,1),E(2,2).(2分)
设直线DE的解析式为y+kx+b,把D(4,1),E(2,2)代入,得
解得,
∴直线DE的解析式为y=﹣x+3.
(2)∵D(4,1),E(2,2),B(4,2),
∴S△ODE=S矩形OABC﹣S△OCE﹣S△BDE﹣S△OAD
=2×4﹣×2×2﹣×1×2﹣×1×4
=3.
∵点F为y轴上一点,S△OEF=S△ODE,
∴S△OEF=×OF×2=3.
∴OF=3.
∴F的坐标为(0,3)或(0,﹣3).
25.(1)证明:∵BE∥AC,AE∥OB,
∴四边形AEBD是平行四边形,
∵四边形OABC是矩形,
∴DA=AC,DB=OB,AC=OB,
∴DA=DB,
∴四边形AEBD是菱形;
(2)解:连接DE,交AB于F,如图所示:
∵四边形AEBD是菱形,
∴AB与DE互相垂直平分,
∵OA=3,OC=2,
∴EF=DF=OA=,AF=AB=1,3+=,
∴点E坐标为:(,1),
设经过点E的反比例函数解析式为:y=,
把点E代入得:k=,
∴经过点E的反比例函数解析式为:y=.
∵四边形OABC是矩形,OA=3,OC=2,
∴B(3,2).
设直线BE的解析式为y=mx+n,将B、E两点的坐标代入,
得,解得,
∴直线BE的解析式为y=﹣x+4.
26.解:(1)∵m=6时,y==1,
∴A(6,1).
∵n=1时,y==6,
∴B(1,6).
∵过点A向y轴作垂线段,过点B向x轴作垂线段,两条垂线段交于点C,
∴C(1,1);
(2)如图.
∵点A,B在反比例函数y=(x>0)的图象上,且横坐标分别为m,n,
∴A(m,),B(n,)(m>0,n>0),
∴D(m,0),E(0,),C(n,).
设直线DE的解析式为y=kx+b,
则,解得,
∴直线DE的解析式为y=﹣x+.
∵点C在直线DE上,
∴=﹣×n+,
化简得m=2n.
把m=2n代入m(n﹣2)=3,整理,得2n2﹣4n﹣3=0,
解得n=,
∵n>0,
∴n=.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
