《第11章反比例函数》期末综合复习能力提升训练2-2020-2021学年苏科版八年级数学下册(Word版 附答案)
文档属性
| 名称 | 《第11章反比例函数》期末综合复习能力提升训练2-2020-2021学年苏科版八年级数学下册(Word版 附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 468.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 14:24:47 | ||
图片预览


文档简介
2021苏科版八年级数学下册《第11章反比例函数》期末综合复习能力提升训练2(附答案)
1.关于反比例函数y=﹣,下列说法中正确的是( )
A.点(1,4)在该函数的图象上
B.当x的值增大时,y的值也增大
C.该函数的图象在一、三象限
D.若点P(m,n) 在该函数的图象上,则点Q(﹣m,﹣n) 也在该函数的图象上
2.已知点(﹣4,a),(4,b),(5,c)在反比例函数y=(k>0)的图象上,则下列结论正确的是( )
A.b<a<c B.a<b<c C.a<c<b D.c<b<a
3.关于x的函数y=k(x﹣1)和y=(k≠0),它们在同一坐标系内的图象大致是( )
A.B.C.D.
4.已知三点(a,m)、(b,n)和(c,t)都在反比例函数y=的图象上,若a<0<b<c,则m、n和t的大小关系是( )
A.t<n<m B.t<m<n C.m<t<n D.m<n<t
5.反比例函数和在第一象限的图象如图所示,点A在函数图象上,点B在函数图象上,AB∥y轴,点C是y轴上的一个动点,则△ABC的面积为( )
A.1 B.2 C.3 D.4
6.在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点M(a,b),则代数式的值为( )
A. B.﹣ C. D.﹣
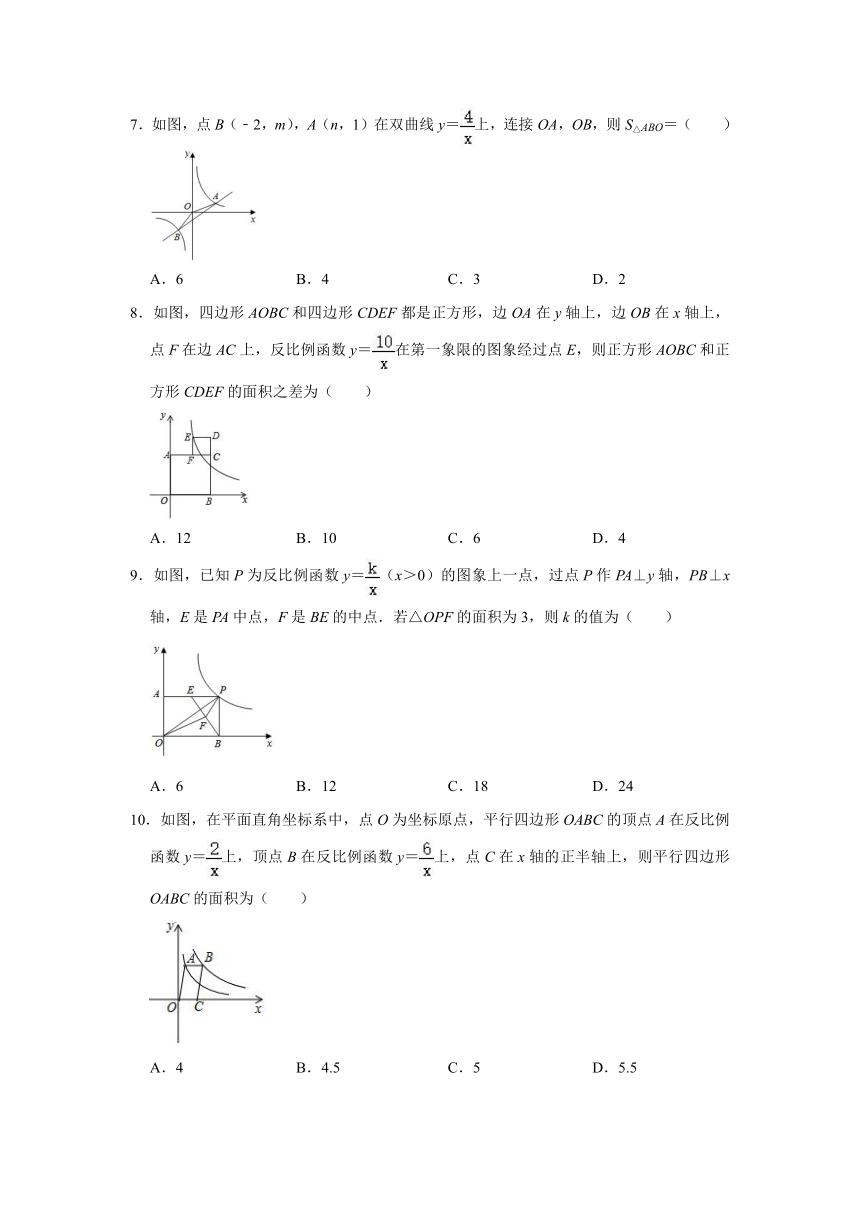
7.如图,点B(﹣2,m),A(n,1)在双曲线y=上,连接OA,OB,则S△ABO=( )
A.6 B.4 C.3 D.2
8.如图,四边形AOBC和四边形CDEF都是正方形,边OA在y轴上,边OB在x轴上,点F在边AC上,反比例函数y=在第一象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )
A.12 B.10 C.6 D.4
9.如图,已知P为反比例函数y=(x>0)的图象上一点,过点P作PA⊥y轴,PB⊥x轴,E是PA中点,F是BE的中点.若△OPF的面积为3,则k的值为( )
A.6 B.12 C.18 D.24
10.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC的面积为( )
A.4 B.4.5 C.5 D.5.5
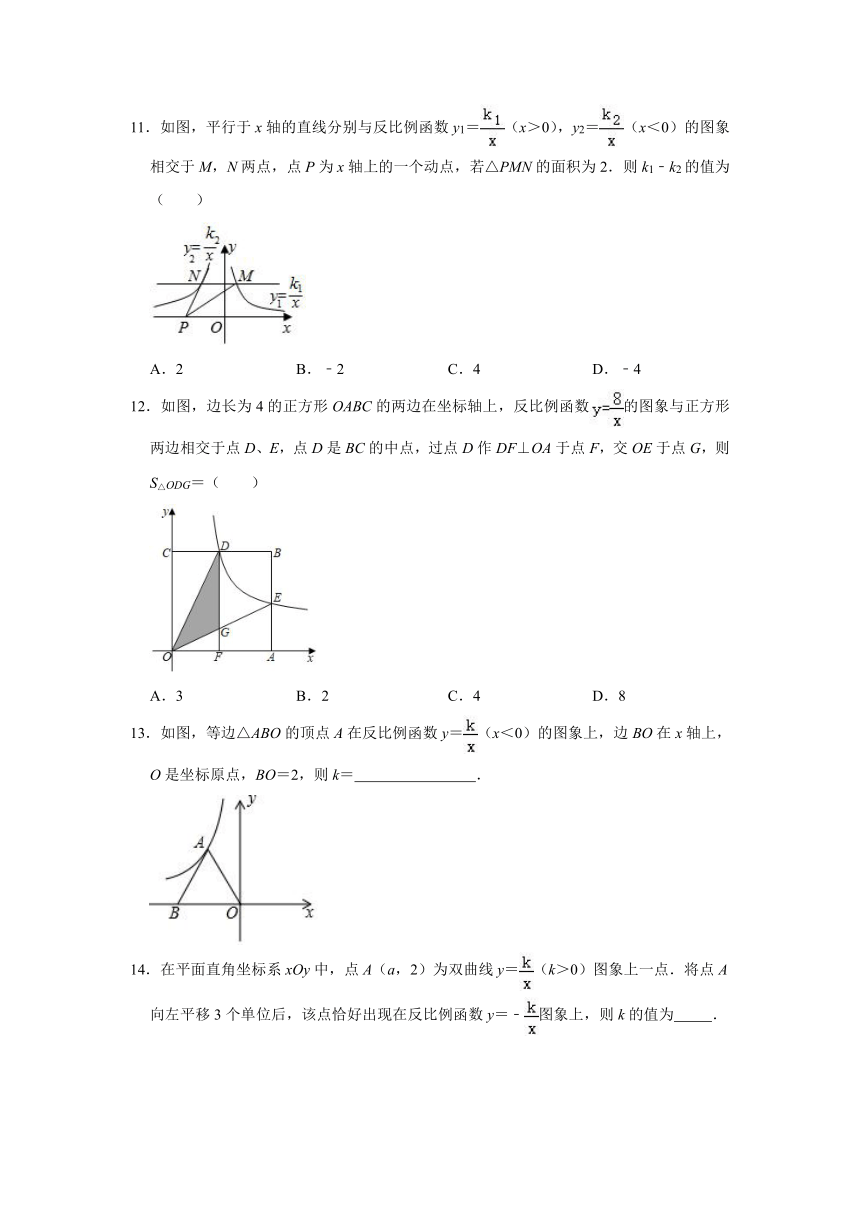
11.如图,平行于x轴的直线分别与反比例函数y1=(x>0),y2=(x<0)的图象相交于M,N两点,点P为x轴上的一个动点,若△PMN的面积为2.则k1﹣k2的值为( )
A.2 B.﹣2 C.4 D.﹣4
12.如图,边长为4的正方形OABC的两边在坐标轴上,反比例函数的图象与正方形两边相交于点D、E,点D是BC的中点,过点D作DF⊥OA于点F,交OE于点G,则S△ODG=( )
A.3 B.2 C.4 D.8
13.如图,等边△ABO的顶点A在反比例函数y=(x<0)的图象上,边BO在x轴上,O是坐标原点,BO=2,则k= .
14.在平面直角坐标系xOy中,点A(a,2)为双曲线y=(k>0)图象上一点.将点A向左平移3个单位后,该点恰好出现在反比例函数y=﹣图象上,则k的值为 .
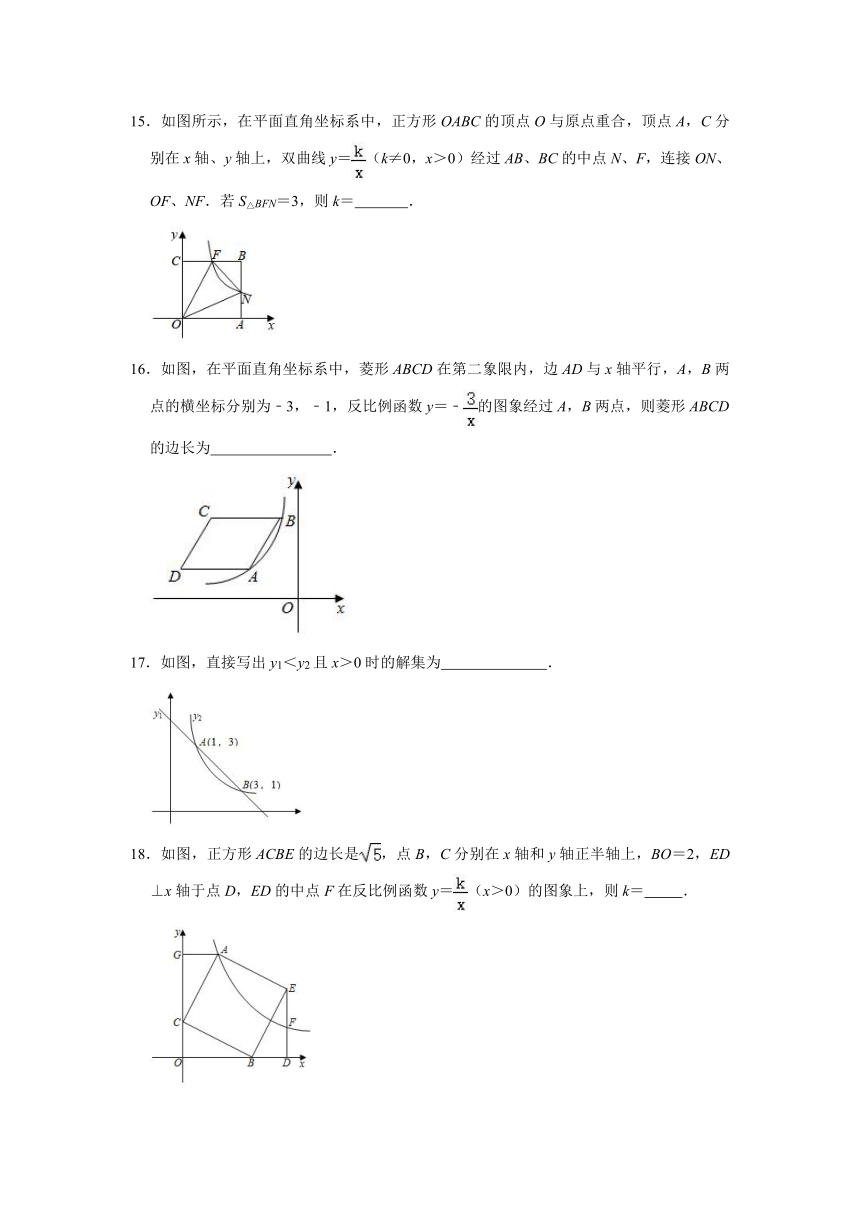
15.如图所示,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,双曲线y=(k≠0,x>0)经过AB、BC的中点N、F,连接ON、OF、NF.若S△BFN=3,则k= .
16.如图,在平面直角坐标系中,菱形ABCD在第二象限内,边AD与x轴平行,A,B两点的横坐标分别为﹣3,﹣1,反比例函数y=﹣的图象经过A,B两点,则菱形ABCD的边长为 .
17.如图,直接写出y1<y2且x>0时的解集为 .
18.如图,正方形ACBE的边长是,点B,C分别在x轴和y轴正半轴上,BO=2,ED⊥x轴于点D,ED的中点F在反比例函数y=(x>0)的图象上,则k= .
19.如图,在Rt△ABC中,∠C=90°,AC=BC,BC∥x轴,点A、B都在反比例函数y=(x>0)上,点C在反比例函数y=(x>0)上,则AB= .
20.如图,直线y=﹣x+b(b>0)与双曲线y=(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,以下结论正确的是 .
A.OA=OB;
B.△AOM≌△BON;
C.若∠AOB=45°,则S△AOB=2k;
D.当AB=时ON﹣BN=1.
21.如图,点A(3,n)在双曲线y=上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC周长的值是 .
22.如图,在平面直角坐标系中,四边形ABCO为平行四边形,A(6,2),B(2,4),反比例函数y=(k≠0)的图象经过四边形OABC的顶点C,则k= .
23.如图,过点P(﹣2,2)分别作x轴,y轴的垂线,交双曲线y=(k>0)于E,F两点.
(1)若k=2,求点E,F的坐标;
(2)若EF=5,求此双曲线的解析式.
24.如图,在平面直角坐标系xOy中,直线y=ax+b与双曲线y=交于A(1,3),B(3,m)两点,与x轴交于点C,与y轴交于点D,连接OA,OB.
(1)求a,b,k的值;
(2)求△OAB的面积;
(3)在x轴上是否存在点P,使△PCD的面积等于△OAB的面积的3倍.若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
25.如图,正比例函数y=2x的图象与反比例函数y=的图象有一个交点为P(2,m).
(1)求反比例函数y=函数表达式;
(2)根据图象,直接写出当﹣4<x<﹣1时,反比例函数y=的y取值范围.
26.已知在平面直角坐标系中,点A(1,2)在反比例函数y=的图象上,过点A的直线与该双曲线的另一支交于点B(﹣2,m).
(1)求直线AB的函数表达式;
(2)若点C为x轴上一动点,求当S△ABC=6时,点C的坐标.
27.如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=(x>0)和y=(x<0)的图象分别交于点P,Q.
(1)求P点的坐标;
(2)若△POQ的面积为9,求k的值.
28.已知A(a,﹣2a)、B(﹣2,a)两点是反比例函数y=与一次函数y=kx+b图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△ABO的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
29.如图,已知反比例函数y1=的图象与直线y2=ax+b相交于点A(﹣2,3),B(1,m).
(1)求出直线y=ax+b的表达式.
(2)直线写出y1>y2时,x的取值范围是 .
(3)在x轴上有一点P使得△PAB的面积为18,求出点P的坐标.
30.已知一次函数y=kx+b与反比例函数y=的图象交于A(﹣3,2)、B(1,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)请观察图象,直接写出不等式kx+b≤的解集.
参考答案
1.解:∵反比例函数为y=﹣,
∴当x=1时,y=﹣4,
∴点(1,﹣4)在该函数的图象上,所以A错误;
∵k=﹣4<0,图象在二、四象限,当x>0时,y随x的增大而增大,所以B、C错误;
∵y=﹣,
∴﹣4=xy,
∵点P(m,n)在它的图象上,
∴﹣4=mn,
又∵点Q(﹣m,﹣n)的横纵坐标值的乘积﹣m?(﹣n)=mn=﹣4,
∴点Q也在函数图象上,故D正确,
故选:D.
2.解:∵k>0,
∴反比例函数的图象在一、三象限,在每一象限内y随x的增大而减小,
∵﹣4<0,
∴点(﹣4,y1)在第三象限,
∴a<0,
∵0<4<5,
∴0<c<b,
∴a<c<b.
故选:C.
3.解:A、反比例函数y=(k≠0)的图象经过第一、三象限,则k>0.所以一次函数y=kx﹣k的图象经过第一、三象限,且与y轴交于负半轴.故本选项不符合题意;
B、反比例函数y=(k≠0)的图象经过第二、四象限,则k<0.所以一次函数y=kx﹣k的图象经过第二、四象限,且与y轴交于正半轴.故本选项不符合题意;
C、反比例函数y=(k≠0)的图象经过第一、三象限,则k>0.所以一次函数y=kx﹣k的图象经过第一、三象限,且与y轴交于负半轴.故本选项符合题意;
D、反比例函数y=(k≠0)的图象经过第二、四象限,则k<0.所以一次函数y=kx﹣k的图象经过第二、四象限,且与y轴交于正半轴.故本选项不符合题意;
故选:C.
4.解:反比例函数y=中,k=2021>0,图象位于一、三象限,
∵a<0,
∴点(a,m)在第三象限,
∴m<0;
∵0<b<c,
∴点(b,n)和点(c,t)在第一象限,
∴0<t<n,
∴m<t<n,
故选:C.
5.解:连接OA、OB,延长AB,交x轴于D,如图,
∵AB∥y轴,
∴AD⊥x轴,OC∥AB,
∴S△OAB=S△ABC,
而S△OAD=×6=3,S△OBD=×4=2,
∴S△OAB=S△OAD﹣S△OBD=1,
∴S△ABC=1,
故选:A.
6.解:∵函数y=(x>0)与y=x﹣1的图象交于点M(a,b),
∴ab=4,b=a﹣1,
∴b﹣a=﹣1,
∴===﹣;
故选:D.
7.解:∵点B(﹣2,m),A(n,1)在双曲线y=上,
∴﹣2m=4,n=4,
∴m=﹣2,
∴B(﹣2,﹣2),A(4,1),
设直线AB的解析式为y=kx+b,
∴,解得,
∴直线AB的解析式为y=x﹣1,
∴直线AB与y轴的交点为(0,﹣1),
∴S△AOB==3,
故选:C.
8.解:设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(a﹣b,a+b),
∴(a+b)?(a﹣b)=10,
整理为a2﹣b2=10,
∵S正方形AOBC=a2,S正方形CDEF=b2,
∴S正方形AOBC﹣S正方形CDEF=10,
故选:B.
9.解:连接OE,
∵P为反比例函数y=(x>0)的图象上一点,点P作PA⊥y轴,PB⊥x轴,
∴S四边形AOBP=PA?PB=k,S△POB=k,
∵E是PA中点,
∴S△PBE=PA?PB=k,S△EOB=OB?OA=k,
∵F是BE的中点,
∴S△FOB=S△EOB=k,S△PFB=S△PEB=k,
∴S△OPF=S△POB﹣S△FOB﹣S△PFB=k﹣k﹣k=k,
∵△OPF的面积为3,
∴k=3,
∴k=24,
故选:D.
10.解:如图,作BD⊥x轴于D,延长BA交y轴于E,
∵四边形OABC是平行四边形,
∴AB∥OC,OA=BC,
∴BE⊥y轴,
∴OE=BD,
∴Rt△AOE≌Rt△CBD(HL),
根据系数k的几何意义,S矩形BDOE=6,S△AOE=1,
∴四边形OABC的面积=6﹣1﹣1=4,
故选:A.
11.解:设:M、N点的坐标分别是M(,m)、N(,m),
则:△PMN的面积=?MN?yM=?(﹣,)?m=2,
则k1﹣k2=4.
故选:C.
12.解:∵边长为4的正方形OABC的两边在坐标轴上,反比例函数的图象与正方形两边相交于点D、E,点D是BC的中点,
∴D(2,4),E(4,2).
又∵过点D作DF⊥OA于点F,交OE于点G,
∴DF=OC=4,GF=AE=×2=1,
∴DG=DF﹣GF=4﹣1=3,
∴S△ODG=?DG?OF=×3×2=3.
故选:A.
13.解:如图,过点A作AD⊥x轴于点D,
∵△AOB是等边三角形,
∴OA=OB=2,∠AOD=60°,
∴OD==1,AD=OA=,
∴A(﹣1,),
∵点A在反比例函数y=(x<0)的图象上,
∴k=﹣.
故答案为:﹣,
14.解:∵点A(a,2)为双曲线y=(k>0)图象上一点,
∴k=2a,
∵点A向左平移3个单位后得到点(a﹣3,2),该点在反比例函数y=﹣图象上,
∴﹣k=2(a﹣3),
∴k=﹣2(a﹣3),
∴2a=﹣2(a﹣3),
∴a=,
∴k=2a=3,
故答案为3.
15.解:∵N、F是AB、BC的中点,
∴BF=BC,BN=,
S△BFN=3,
∴BF?BN=??=3,
∴BC?AB=24,
∵四边形ABCO是正方形,
∴OA=AB=BC=CO=2,
∵N是AB中点,
∴AN=BN=,
∴N(2,),
把N(2,)代入y=,得到k=12,
故答案为12.
16.解:过点A、B分别作x轴、y轴的平行线AM、BN相交于点E,交x轴,y轴于点N、M,
∵A,B两点的横坐标分别为﹣3,﹣1,反比例函数y=﹣的图象经过A,B两点,
∴A(﹣3,1),B(﹣1,3),
∴AM=3,BN=3,OM=ON=1,
∴AE=BE=3﹣1=2,
在Rt△ABE中,AB===2,
故答案为:2.
17.解:由图象可得,当x>0时,y1<y2的解集为0<x<1或x>3;
故答案为0<x<1或x>3.
18.解:∵正方形ACBE的边长是,BO=2,
∴BC=BE=,
∴OC===1,
∵∠ABC=90°,
∴∠OBC+∠EBD=90°,
∵∠OBC+∠OCB=90°,
∴∠OCB=∠EBD,
在△OBC和△DEB中,
,
∴△OBC≌△DEB(AAS),
∴BD=OC=1,DE=OB=2,
∴OD=3,
∴E(3,2),
∵点F是ED的中点,
∴F(3,1),
∵点F在反比例函数y=(x>0)的图象上,
∴k=3×1=3,
故答案为3.
19.解:设C(a,),AC=BC=m,
∴A(a,+m),B(a+m,),
∵点A、B都在反比例函数y=上,
∴a(+m)=(a+m)?=10,
解得m=,
∴AC=BC=,
在Rt△ABC中,AB==,
故答案为.
20.解:A.设A(x1,y1),B(x2,y2),代入y=中,得x1?y1=x2?y2=k,
联立 ,得x2﹣bx+k=0,
则x1?x2=k,又x1?y1=k,
∴x2=y1,
同理x2?y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
∴OA=OB,
故A正确,符合题意;
B.由A知:ON=OM,AM=BN,OA=OB,
∴△AOM≌△BON(SSS),
故B正确,符合题意;
C.过点O作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
由B知,△AOM≌△BON,
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN(AAS),
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=k+k=k,
故C错误,不符合题意;
D.延长MA,交NB的延长线于G点,
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=时,GA=GB=1,
∴ON﹣BN=GN﹣BN=GB=1,
故D正确,符合题意.
故答案为:A、B、D.
21.解:∵点A(3,n)在双曲线y=上,
∴n=1,
∴A(3,1),
∴OC=3,AC=1.
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=AB+BC+AC=OB+BC+AC=OC+AC=3+1=4.
故答案为4.
22.解:连接OB,AC,相交于点P,
∵四边形OABC是平行四边形,
∴AP=CP,OP=BP,
∵B(2,4),
∴P的坐标(1,2),
∵A(6,2),
∴C的坐标为(﹣4,2),
∵反比例函数y=(k≠0)的图象经过点C,
∴k=﹣4×2=﹣8,
故答案为:﹣8.
23.解:(1)若k=2,则y=,
∵P(﹣2,2),
∴E点横坐标为﹣2,F点纵坐标2,
∴当x=﹣2时,y=﹣1;当y=2时,x=1,
故E(﹣2,﹣1);F(1,2).
(2)因为E、F都在y=上,设E(﹣2,﹣),F(,2),
所以EF===5,
解得:k=6或k=﹣14,
∵k>0,
∴k=6,
故此双曲线的解析式为:y=.
24.解:(1)将点A(1,3)代入y=得:3=,
解得k=3,
故反比例函数的表达式为:y=,
将点B(3,m)代入y=得:m=1,
故点B(3,1),
将点A(1,3),B(3,1)代入y=ax+b得,
解得;
故a=﹣1,b=4,k=3;
(2)由一次函数y=﹣x+4可知,D(0,4),C(4,0),
则△AOB的面积=△BOD的面积﹣△AOD的面积=﹣=4;
(3)∵△PCD的面积等于△OAB的面积的3倍.
∴PC?OD=12,即=12,
∴PC=6,
∴P(﹣2,0)或(10,0).
25.解:(1)将点P(2,m)代入y=2x,
∴m=4,
∴点P坐标为(2,4),
将点P(2,4)代入y=,
∴k=2×4=8,
∴反比例函数为y=;
(2)当﹣4<x<﹣1时,反比例函数图象在第三象限,
∵x=﹣4时,y=,当x=﹣1时,y==﹣8,
∴当﹣4<x<﹣1时,y的取值范围是﹣8<y<﹣2.
26.解:(1)把点A(1,2)代入y=中,
解得k=2,
∴反比例函数表达式为y=,
把点B(﹣2,m)代入y=中,
解得m=﹣1,
∴点B的坐标为(﹣2,﹣1),
设直线AB的表达式为y=kx+b,
把A(1,2)和B(﹣2,﹣1)代入上式,
得,
解得,
∴一次函数表达式为y=x+1;
(2)设点C的坐标为(a,0),如图,
当y=0时,x+1=0,
解得x=﹣1,
∴点D的坐标为(﹣1,0),
则CD=|a+1|,
∵S△ABC=S△ADC+S△BDC=6,
即,
∴CD=4,
∴|a+1|=4,a+1=±4,
解得a1=3,a2=﹣5,
∴点C的坐标为(3,0)或(﹣5,0).
27.解:(1)∵PQ∥x轴,
∴点P的纵坐标为2,
把y=2代入y=得x=3,
∴P点坐标为(3,2);
(2)∵S△POQ=S△OMQ+S△OMP,
∴|k|+×|6|=9,
∴|k|=12,
而k<0,
∴k=﹣12.
28.解:(1)∵A(a,﹣2a)、B(﹣2,a)两点在反比例函数y=的图象上,
∴m=﹣2a?a=﹣2a,
解得a=1,m=﹣2,
∴A(1,﹣2),B(﹣2,1),反比例函数的解析式为y=﹣.
将点A(1,﹣2)、点B(﹣2,1)代入到y=kx+b中,
得:,解得:,
∴一次函数的解析式为y=﹣x﹣1.
(2)在直线y=﹣x﹣1中,令y=0,则﹣x﹣1=0,解得x=﹣1,
∴C(﹣1,0),
∴S△AOB=S△AOC+S△BOC=×1×2+×1=;
(3)观察函数图象,发现:
当x<﹣2或0<x<1时,反比例函数图象在一次函数图象的上方,
∴不等式kx+b﹣>0的解集为x<﹣2或0<x<1.
29.解:(1)将点A(﹣2,3)代入y1=得:3=,
∴k=﹣6,
故反比例函数表达式为:y=﹣,
将点B(1,m)代入上式得:m=﹣6,
故点B(1,﹣6),
将点A、B的坐标代入y=ax+b得,解得,
故直线的表达式为:y=﹣3x﹣3;
(2)由图象可知,y1>y2时,x的取值范围﹣2<x<0或x>1,
故答案为﹣2<x<0或x>1;
(3)连接AP、BP,
设直线与x轴的交点为E,当y=0时,x=﹣1,故点E(﹣1,0),
分别过点A、B作x轴的垂线AC、BD,垂足分别为C、D,
则S△PAB=PE?CA+PE?BD=PE+PE=PE=18,
解得:PE=4,
故点P的坐标为(3,0)或(﹣5,0).
30.解:(1)∵反比例函数y=的图象经过点A(﹣3,2),
∴m=﹣3×2=﹣6,
∵点B(1,n)在反比例函数图象上,
∴n=﹣6.
∴B(1,﹣6),
把A,B的坐标代入y=kx+b,则,解得,
∴一次函数的解析式为y=﹣2x﹣4,反比例函数的解析式为y=﹣;
(2)如图设直线AB交y轴于C,则C(0,﹣4),
∴S△AOB=S△OCA+S△OCB=×4×3+×4×1=8;
(3)观察函数图象知,不等式kx+b≤的解集为﹣3≤x<0或x≥1.
1.关于反比例函数y=﹣,下列说法中正确的是( )
A.点(1,4)在该函数的图象上
B.当x的值增大时,y的值也增大
C.该函数的图象在一、三象限
D.若点P(m,n) 在该函数的图象上,则点Q(﹣m,﹣n) 也在该函数的图象上
2.已知点(﹣4,a),(4,b),(5,c)在反比例函数y=(k>0)的图象上,则下列结论正确的是( )
A.b<a<c B.a<b<c C.a<c<b D.c<b<a
3.关于x的函数y=k(x﹣1)和y=(k≠0),它们在同一坐标系内的图象大致是( )
A.B.C.D.
4.已知三点(a,m)、(b,n)和(c,t)都在反比例函数y=的图象上,若a<0<b<c,则m、n和t的大小关系是( )
A.t<n<m B.t<m<n C.m<t<n D.m<n<t
5.反比例函数和在第一象限的图象如图所示,点A在函数图象上,点B在函数图象上,AB∥y轴,点C是y轴上的一个动点,则△ABC的面积为( )
A.1 B.2 C.3 D.4
6.在平面直角坐标系中,函数y=(x>0)与y=x﹣1的图象交于点M(a,b),则代数式的值为( )
A. B.﹣ C. D.﹣
7.如图,点B(﹣2,m),A(n,1)在双曲线y=上,连接OA,OB,则S△ABO=( )
A.6 B.4 C.3 D.2
8.如图,四边形AOBC和四边形CDEF都是正方形,边OA在y轴上,边OB在x轴上,点F在边AC上,反比例函数y=在第一象限的图象经过点E,则正方形AOBC和正方形CDEF的面积之差为( )
A.12 B.10 C.6 D.4
9.如图,已知P为反比例函数y=(x>0)的图象上一点,过点P作PA⊥y轴,PB⊥x轴,E是PA中点,F是BE的中点.若△OPF的面积为3,则k的值为( )
A.6 B.12 C.18 D.24
10.如图,在平面直角坐标系中,点O为坐标原点,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC的面积为( )
A.4 B.4.5 C.5 D.5.5
11.如图,平行于x轴的直线分别与反比例函数y1=(x>0),y2=(x<0)的图象相交于M,N两点,点P为x轴上的一个动点,若△PMN的面积为2.则k1﹣k2的值为( )
A.2 B.﹣2 C.4 D.﹣4
12.如图,边长为4的正方形OABC的两边在坐标轴上,反比例函数的图象与正方形两边相交于点D、E,点D是BC的中点,过点D作DF⊥OA于点F,交OE于点G,则S△ODG=( )
A.3 B.2 C.4 D.8
13.如图,等边△ABO的顶点A在反比例函数y=(x<0)的图象上,边BO在x轴上,O是坐标原点,BO=2,则k= .
14.在平面直角坐标系xOy中,点A(a,2)为双曲线y=(k>0)图象上一点.将点A向左平移3个单位后,该点恰好出现在反比例函数y=﹣图象上,则k的值为 .
15.如图所示,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,双曲线y=(k≠0,x>0)经过AB、BC的中点N、F,连接ON、OF、NF.若S△BFN=3,则k= .
16.如图,在平面直角坐标系中,菱形ABCD在第二象限内,边AD与x轴平行,A,B两点的横坐标分别为﹣3,﹣1,反比例函数y=﹣的图象经过A,B两点,则菱形ABCD的边长为 .
17.如图,直接写出y1<y2且x>0时的解集为 .
18.如图,正方形ACBE的边长是,点B,C分别在x轴和y轴正半轴上,BO=2,ED⊥x轴于点D,ED的中点F在反比例函数y=(x>0)的图象上,则k= .
19.如图,在Rt△ABC中,∠C=90°,AC=BC,BC∥x轴,点A、B都在反比例函数y=(x>0)上,点C在反比例函数y=(x>0)上,则AB= .
20.如图,直线y=﹣x+b(b>0)与双曲线y=(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,以下结论正确的是 .
A.OA=OB;
B.△AOM≌△BON;
C.若∠AOB=45°,则S△AOB=2k;
D.当AB=时ON﹣BN=1.
21.如图,点A(3,n)在双曲线y=上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点B,则△ABC周长的值是 .
22.如图,在平面直角坐标系中,四边形ABCO为平行四边形,A(6,2),B(2,4),反比例函数y=(k≠0)的图象经过四边形OABC的顶点C,则k= .
23.如图,过点P(﹣2,2)分别作x轴,y轴的垂线,交双曲线y=(k>0)于E,F两点.
(1)若k=2,求点E,F的坐标;
(2)若EF=5,求此双曲线的解析式.
24.如图,在平面直角坐标系xOy中,直线y=ax+b与双曲线y=交于A(1,3),B(3,m)两点,与x轴交于点C,与y轴交于点D,连接OA,OB.
(1)求a,b,k的值;
(2)求△OAB的面积;
(3)在x轴上是否存在点P,使△PCD的面积等于△OAB的面积的3倍.若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
25.如图,正比例函数y=2x的图象与反比例函数y=的图象有一个交点为P(2,m).
(1)求反比例函数y=函数表达式;
(2)根据图象,直接写出当﹣4<x<﹣1时,反比例函数y=的y取值范围.
26.已知在平面直角坐标系中,点A(1,2)在反比例函数y=的图象上,过点A的直线与该双曲线的另一支交于点B(﹣2,m).
(1)求直线AB的函数表达式;
(2)若点C为x轴上一动点,求当S△ABC=6时,点C的坐标.
27.如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=(x>0)和y=(x<0)的图象分别交于点P,Q.
(1)求P点的坐标;
(2)若△POQ的面积为9,求k的值.
28.已知A(a,﹣2a)、B(﹣2,a)两点是反比例函数y=与一次函数y=kx+b图象的两个交点.
(1)求一次函数和反比例函数的解析式;
(2)求△ABO的面积;
(3)观察图象,直接写出不等式kx+b﹣>0的解集.
29.如图,已知反比例函数y1=的图象与直线y2=ax+b相交于点A(﹣2,3),B(1,m).
(1)求出直线y=ax+b的表达式.
(2)直线写出y1>y2时,x的取值范围是 .
(3)在x轴上有一点P使得△PAB的面积为18,求出点P的坐标.
30.已知一次函数y=kx+b与反比例函数y=的图象交于A(﹣3,2)、B(1,n)两点.
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)请观察图象,直接写出不等式kx+b≤的解集.
参考答案
1.解:∵反比例函数为y=﹣,
∴当x=1时,y=﹣4,
∴点(1,﹣4)在该函数的图象上,所以A错误;
∵k=﹣4<0,图象在二、四象限,当x>0时,y随x的增大而增大,所以B、C错误;
∵y=﹣,
∴﹣4=xy,
∵点P(m,n)在它的图象上,
∴﹣4=mn,
又∵点Q(﹣m,﹣n)的横纵坐标值的乘积﹣m?(﹣n)=mn=﹣4,
∴点Q也在函数图象上,故D正确,
故选:D.
2.解:∵k>0,
∴反比例函数的图象在一、三象限,在每一象限内y随x的增大而减小,
∵﹣4<0,
∴点(﹣4,y1)在第三象限,
∴a<0,
∵0<4<5,
∴0<c<b,
∴a<c<b.
故选:C.
3.解:A、反比例函数y=(k≠0)的图象经过第一、三象限,则k>0.所以一次函数y=kx﹣k的图象经过第一、三象限,且与y轴交于负半轴.故本选项不符合题意;
B、反比例函数y=(k≠0)的图象经过第二、四象限,则k<0.所以一次函数y=kx﹣k的图象经过第二、四象限,且与y轴交于正半轴.故本选项不符合题意;
C、反比例函数y=(k≠0)的图象经过第一、三象限,则k>0.所以一次函数y=kx﹣k的图象经过第一、三象限,且与y轴交于负半轴.故本选项符合题意;
D、反比例函数y=(k≠0)的图象经过第二、四象限,则k<0.所以一次函数y=kx﹣k的图象经过第二、四象限,且与y轴交于正半轴.故本选项不符合题意;
故选:C.
4.解:反比例函数y=中,k=2021>0,图象位于一、三象限,
∵a<0,
∴点(a,m)在第三象限,
∴m<0;
∵0<b<c,
∴点(b,n)和点(c,t)在第一象限,
∴0<t<n,
∴m<t<n,
故选:C.
5.解:连接OA、OB,延长AB,交x轴于D,如图,
∵AB∥y轴,
∴AD⊥x轴,OC∥AB,
∴S△OAB=S△ABC,
而S△OAD=×6=3,S△OBD=×4=2,
∴S△OAB=S△OAD﹣S△OBD=1,
∴S△ABC=1,
故选:A.
6.解:∵函数y=(x>0)与y=x﹣1的图象交于点M(a,b),
∴ab=4,b=a﹣1,
∴b﹣a=﹣1,
∴===﹣;
故选:D.
7.解:∵点B(﹣2,m),A(n,1)在双曲线y=上,
∴﹣2m=4,n=4,
∴m=﹣2,
∴B(﹣2,﹣2),A(4,1),
设直线AB的解析式为y=kx+b,
∴,解得,
∴直线AB的解析式为y=x﹣1,
∴直线AB与y轴的交点为(0,﹣1),
∴S△AOB==3,
故选:C.
8.解:设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(a﹣b,a+b),
∴(a+b)?(a﹣b)=10,
整理为a2﹣b2=10,
∵S正方形AOBC=a2,S正方形CDEF=b2,
∴S正方形AOBC﹣S正方形CDEF=10,
故选:B.
9.解:连接OE,
∵P为反比例函数y=(x>0)的图象上一点,点P作PA⊥y轴,PB⊥x轴,
∴S四边形AOBP=PA?PB=k,S△POB=k,
∵E是PA中点,
∴S△PBE=PA?PB=k,S△EOB=OB?OA=k,
∵F是BE的中点,
∴S△FOB=S△EOB=k,S△PFB=S△PEB=k,
∴S△OPF=S△POB﹣S△FOB﹣S△PFB=k﹣k﹣k=k,
∵△OPF的面积为3,
∴k=3,
∴k=24,
故选:D.
10.解:如图,作BD⊥x轴于D,延长BA交y轴于E,
∵四边形OABC是平行四边形,
∴AB∥OC,OA=BC,
∴BE⊥y轴,
∴OE=BD,
∴Rt△AOE≌Rt△CBD(HL),
根据系数k的几何意义,S矩形BDOE=6,S△AOE=1,
∴四边形OABC的面积=6﹣1﹣1=4,
故选:A.
11.解:设:M、N点的坐标分别是M(,m)、N(,m),
则:△PMN的面积=?MN?yM=?(﹣,)?m=2,
则k1﹣k2=4.
故选:C.
12.解:∵边长为4的正方形OABC的两边在坐标轴上,反比例函数的图象与正方形两边相交于点D、E,点D是BC的中点,
∴D(2,4),E(4,2).
又∵过点D作DF⊥OA于点F,交OE于点G,
∴DF=OC=4,GF=AE=×2=1,
∴DG=DF﹣GF=4﹣1=3,
∴S△ODG=?DG?OF=×3×2=3.
故选:A.
13.解:如图,过点A作AD⊥x轴于点D,
∵△AOB是等边三角形,
∴OA=OB=2,∠AOD=60°,
∴OD==1,AD=OA=,
∴A(﹣1,),
∵点A在反比例函数y=(x<0)的图象上,
∴k=﹣.
故答案为:﹣,
14.解:∵点A(a,2)为双曲线y=(k>0)图象上一点,
∴k=2a,
∵点A向左平移3个单位后得到点(a﹣3,2),该点在反比例函数y=﹣图象上,
∴﹣k=2(a﹣3),
∴k=﹣2(a﹣3),
∴2a=﹣2(a﹣3),
∴a=,
∴k=2a=3,
故答案为3.
15.解:∵N、F是AB、BC的中点,
∴BF=BC,BN=,
S△BFN=3,
∴BF?BN=??=3,
∴BC?AB=24,
∵四边形ABCO是正方形,
∴OA=AB=BC=CO=2,
∵N是AB中点,
∴AN=BN=,
∴N(2,),
把N(2,)代入y=,得到k=12,
故答案为12.
16.解:过点A、B分别作x轴、y轴的平行线AM、BN相交于点E,交x轴,y轴于点N、M,
∵A,B两点的横坐标分别为﹣3,﹣1,反比例函数y=﹣的图象经过A,B两点,
∴A(﹣3,1),B(﹣1,3),
∴AM=3,BN=3,OM=ON=1,
∴AE=BE=3﹣1=2,
在Rt△ABE中,AB===2,
故答案为:2.
17.解:由图象可得,当x>0时,y1<y2的解集为0<x<1或x>3;
故答案为0<x<1或x>3.
18.解:∵正方形ACBE的边长是,BO=2,
∴BC=BE=,
∴OC===1,
∵∠ABC=90°,
∴∠OBC+∠EBD=90°,
∵∠OBC+∠OCB=90°,
∴∠OCB=∠EBD,
在△OBC和△DEB中,
,
∴△OBC≌△DEB(AAS),
∴BD=OC=1,DE=OB=2,
∴OD=3,
∴E(3,2),
∵点F是ED的中点,
∴F(3,1),
∵点F在反比例函数y=(x>0)的图象上,
∴k=3×1=3,
故答案为3.
19.解:设C(a,),AC=BC=m,
∴A(a,+m),B(a+m,),
∵点A、B都在反比例函数y=上,
∴a(+m)=(a+m)?=10,
解得m=,
∴AC=BC=,
在Rt△ABC中,AB==,
故答案为.
20.解:A.设A(x1,y1),B(x2,y2),代入y=中,得x1?y1=x2?y2=k,
联立 ,得x2﹣bx+k=0,
则x1?x2=k,又x1?y1=k,
∴x2=y1,
同理x2?y2=k,
可得x1=y2,
∴ON=OM,AM=BN,
∴OA=OB,
故A正确,符合题意;
B.由A知:ON=OM,AM=BN,OA=OB,
∴△AOM≌△BON(SSS),
故B正确,符合题意;
C.过点O作OH⊥AB,垂足为H,
∵OA=OB,∠AOB=45°,
由B知,△AOM≌△BON,
∴∠MOA=∠BON=22.5°,
∠AOH=∠BOH=22.5°,
∴△OAM≌△OAH≌△OBH≌△OBN(AAS),
∴S△AOB=S△AOH+S△BOH=S△AOM+S△BON=k+k=k,
故C错误,不符合题意;
D.延长MA,交NB的延长线于G点,
∵NG=OM=ON=MG,BN=AM,
∴GB=GA,
∴△ABG为等腰直角三角形,
当AB=时,GA=GB=1,
∴ON﹣BN=GN﹣BN=GB=1,
故D正确,符合题意.
故答案为:A、B、D.
21.解:∵点A(3,n)在双曲线y=上,
∴n=1,
∴A(3,1),
∴OC=3,AC=1.
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=AB+BC+AC=OB+BC+AC=OC+AC=3+1=4.
故答案为4.
22.解:连接OB,AC,相交于点P,
∵四边形OABC是平行四边形,
∴AP=CP,OP=BP,
∵B(2,4),
∴P的坐标(1,2),
∵A(6,2),
∴C的坐标为(﹣4,2),
∵反比例函数y=(k≠0)的图象经过点C,
∴k=﹣4×2=﹣8,
故答案为:﹣8.
23.解:(1)若k=2,则y=,
∵P(﹣2,2),
∴E点横坐标为﹣2,F点纵坐标2,
∴当x=﹣2时,y=﹣1;当y=2时,x=1,
故E(﹣2,﹣1);F(1,2).
(2)因为E、F都在y=上,设E(﹣2,﹣),F(,2),
所以EF===5,
解得:k=6或k=﹣14,
∵k>0,
∴k=6,
故此双曲线的解析式为:y=.
24.解:(1)将点A(1,3)代入y=得:3=,
解得k=3,
故反比例函数的表达式为:y=,
将点B(3,m)代入y=得:m=1,
故点B(3,1),
将点A(1,3),B(3,1)代入y=ax+b得,
解得;
故a=﹣1,b=4,k=3;
(2)由一次函数y=﹣x+4可知,D(0,4),C(4,0),
则△AOB的面积=△BOD的面积﹣△AOD的面积=﹣=4;
(3)∵△PCD的面积等于△OAB的面积的3倍.
∴PC?OD=12,即=12,
∴PC=6,
∴P(﹣2,0)或(10,0).
25.解:(1)将点P(2,m)代入y=2x,
∴m=4,
∴点P坐标为(2,4),
将点P(2,4)代入y=,
∴k=2×4=8,
∴反比例函数为y=;
(2)当﹣4<x<﹣1时,反比例函数图象在第三象限,
∵x=﹣4时,y=,当x=﹣1时,y==﹣8,
∴当﹣4<x<﹣1时,y的取值范围是﹣8<y<﹣2.
26.解:(1)把点A(1,2)代入y=中,
解得k=2,
∴反比例函数表达式为y=,
把点B(﹣2,m)代入y=中,
解得m=﹣1,
∴点B的坐标为(﹣2,﹣1),
设直线AB的表达式为y=kx+b,
把A(1,2)和B(﹣2,﹣1)代入上式,
得,
解得,
∴一次函数表达式为y=x+1;
(2)设点C的坐标为(a,0),如图,
当y=0时,x+1=0,
解得x=﹣1,
∴点D的坐标为(﹣1,0),
则CD=|a+1|,
∵S△ABC=S△ADC+S△BDC=6,
即,
∴CD=4,
∴|a+1|=4,a+1=±4,
解得a1=3,a2=﹣5,
∴点C的坐标为(3,0)或(﹣5,0).
27.解:(1)∵PQ∥x轴,
∴点P的纵坐标为2,
把y=2代入y=得x=3,
∴P点坐标为(3,2);
(2)∵S△POQ=S△OMQ+S△OMP,
∴|k|+×|6|=9,
∴|k|=12,
而k<0,
∴k=﹣12.
28.解:(1)∵A(a,﹣2a)、B(﹣2,a)两点在反比例函数y=的图象上,
∴m=﹣2a?a=﹣2a,
解得a=1,m=﹣2,
∴A(1,﹣2),B(﹣2,1),反比例函数的解析式为y=﹣.
将点A(1,﹣2)、点B(﹣2,1)代入到y=kx+b中,
得:,解得:,
∴一次函数的解析式为y=﹣x﹣1.
(2)在直线y=﹣x﹣1中,令y=0,则﹣x﹣1=0,解得x=﹣1,
∴C(﹣1,0),
∴S△AOB=S△AOC+S△BOC=×1×2+×1=;
(3)观察函数图象,发现:
当x<﹣2或0<x<1时,反比例函数图象在一次函数图象的上方,
∴不等式kx+b﹣>0的解集为x<﹣2或0<x<1.
29.解:(1)将点A(﹣2,3)代入y1=得:3=,
∴k=﹣6,
故反比例函数表达式为:y=﹣,
将点B(1,m)代入上式得:m=﹣6,
故点B(1,﹣6),
将点A、B的坐标代入y=ax+b得,解得,
故直线的表达式为:y=﹣3x﹣3;
(2)由图象可知,y1>y2时,x的取值范围﹣2<x<0或x>1,
故答案为﹣2<x<0或x>1;
(3)连接AP、BP,
设直线与x轴的交点为E,当y=0时,x=﹣1,故点E(﹣1,0),
分别过点A、B作x轴的垂线AC、BD,垂足分别为C、D,
则S△PAB=PE?CA+PE?BD=PE+PE=PE=18,
解得:PE=4,
故点P的坐标为(3,0)或(﹣5,0).
30.解:(1)∵反比例函数y=的图象经过点A(﹣3,2),
∴m=﹣3×2=﹣6,
∵点B(1,n)在反比例函数图象上,
∴n=﹣6.
∴B(1,﹣6),
把A,B的坐标代入y=kx+b,则,解得,
∴一次函数的解析式为y=﹣2x﹣4,反比例函数的解析式为y=﹣;
(2)如图设直线AB交y轴于C,则C(0,﹣4),
∴S△AOB=S△OCA+S△OCB=×4×3+×4×1=8;
(3)观察函数图象知,不等式kx+b≤的解集为﹣3≤x<0或x≥1.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
