2020-2021学年上海市浦东新区第四教育署七年级(下)调研数学试卷(5月份)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市浦东新区第四教育署七年级(下)调研数学试卷(5月份)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 270.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览


文档简介
2020-2021学年上海市浦东新区第四教育署七年级(下)调研数学试卷(5月份)
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.(2分)在下列实数中,无理数是( )
A.3 B. C.0 D.﹣
2.(2分)下列各式中,计算正确的是( )
A.×= B.=﹣2 C.=3 D.﹣=
3.(2分)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
4.(2分)如果∠A=∠B﹣∠C,那么△ABC是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
5.(2分)下列说法中,正确的个数是( )
①在同一平面内,不相交的两条直线一定平行;
②过一点有且只有一条直线与已知直线平行;
③两条平行线被第三条直线所截,一对内错角的角平分线互相平行;
④从直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
A.1个 B.2个 C.3个 D.4个
6.(2分)如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
二、填空题(本大题共有12小题,每题3分,共36分)
7.(3分)把化成幂的形式是 .
8.(3分)若x3=﹣,则x的值为 .
9.(3分)计算:(﹣3)﹣1+×= .
10.(3分)若与|2x+y﹣6|互为相反数,则(x+y)2的平方根是 .
11.(3分)近似数0.730的有效数字有 个.
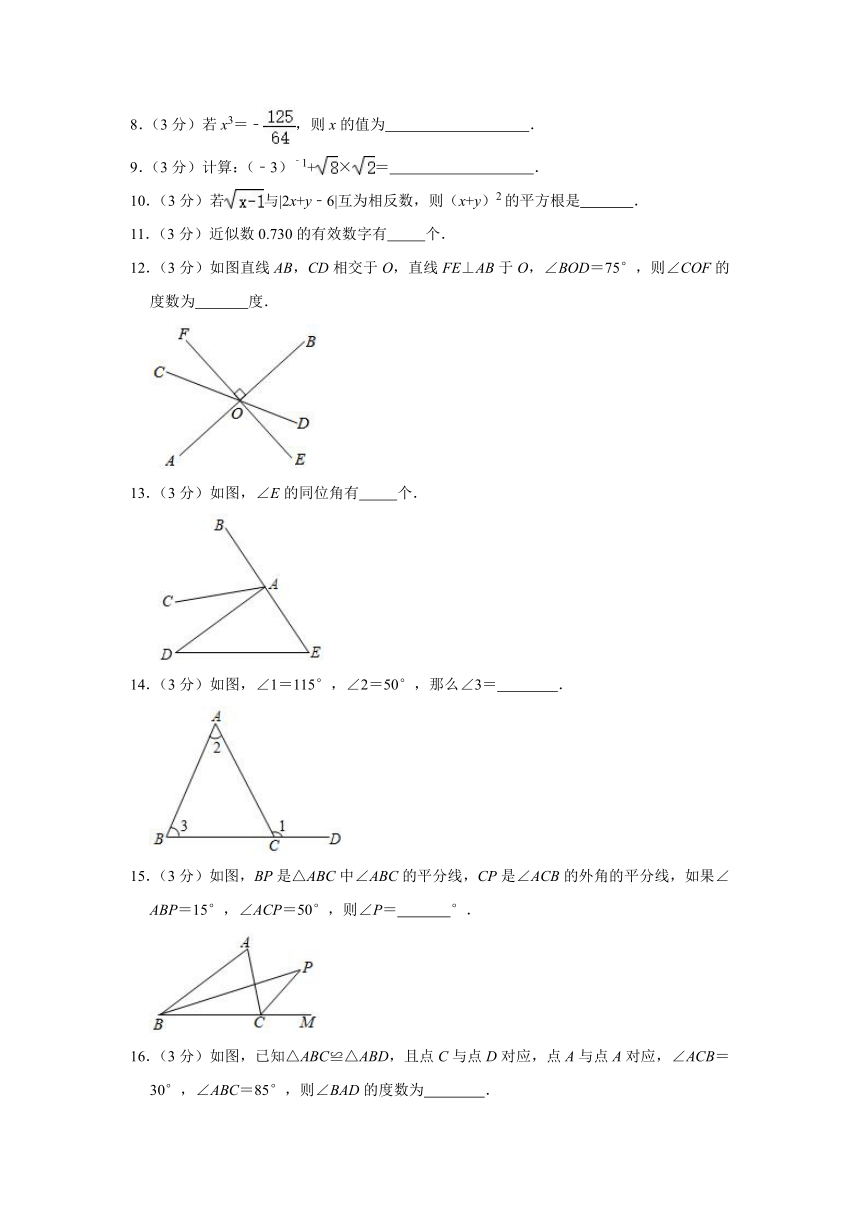
12.(3分)如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为 度.
13.(3分)如图,∠E的同位角有 个.
14.(3分)如图,∠1=115°,∠2=50°,那么∠3= .
15.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= °.
16.(3分)如图,已知△ABC≌△ABD,且点C与点D对应,点A与点A对应,∠ACB=30°,∠ABC=85°,则∠BAD的度数为 .
17.(3分)如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF= .
18.(3分)如图,若AB,CD相交于点E,若△ABC≌△ADE,且点B与点D对应,点C与点E对应,∠BAC=28°,则∠B的度数是 °.
三、解答题(本大题共8小题,第19、20题每题5分,第21至24分每题6分,第25题8分,第26题10分,共52分)
19.(5分)计算:.
20.(5分)计算:﹣12021﹣+(π﹣3.14)0﹣(﹣)﹣2.
21.(6分)利用幂的运算性质进行计算:×÷×8.
22.(6分)如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB ( ),
所以∠1+ =180° ( ).
因为∠1=∠A(已知),
所以∠A+ =180° ( ).
所以DE∥AC ( ).
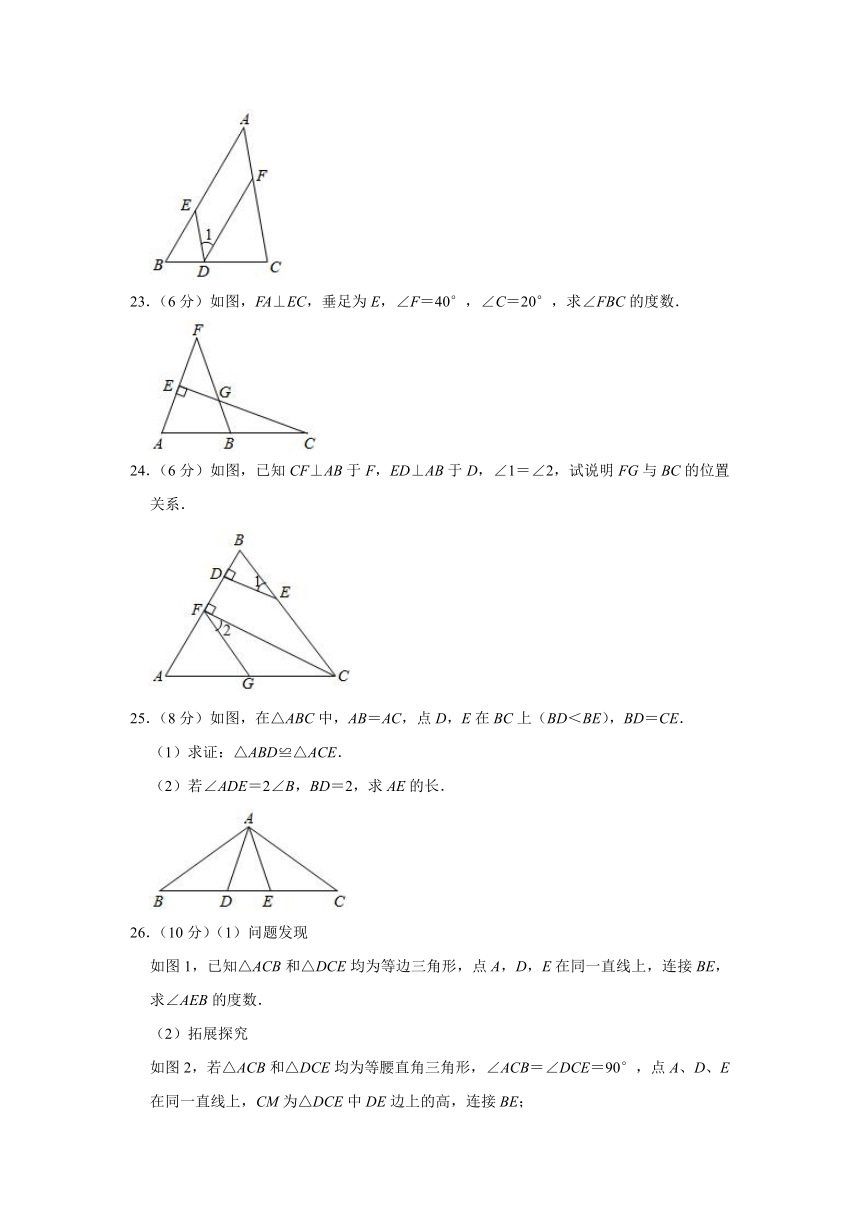
23.(6分)如图,FA⊥EC,垂足为E,∠F=40°,∠C=20°,求∠FBC的度数.
24.(6分)如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,试说明FG与BC的位置关系.
25.(8分)如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.
(1)求证:△ABD≌△ACE.
(2)若∠ADE=2∠B,BD=2,求AE的长.
26.(10分)(1)问题发现
如图1,已知△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE;
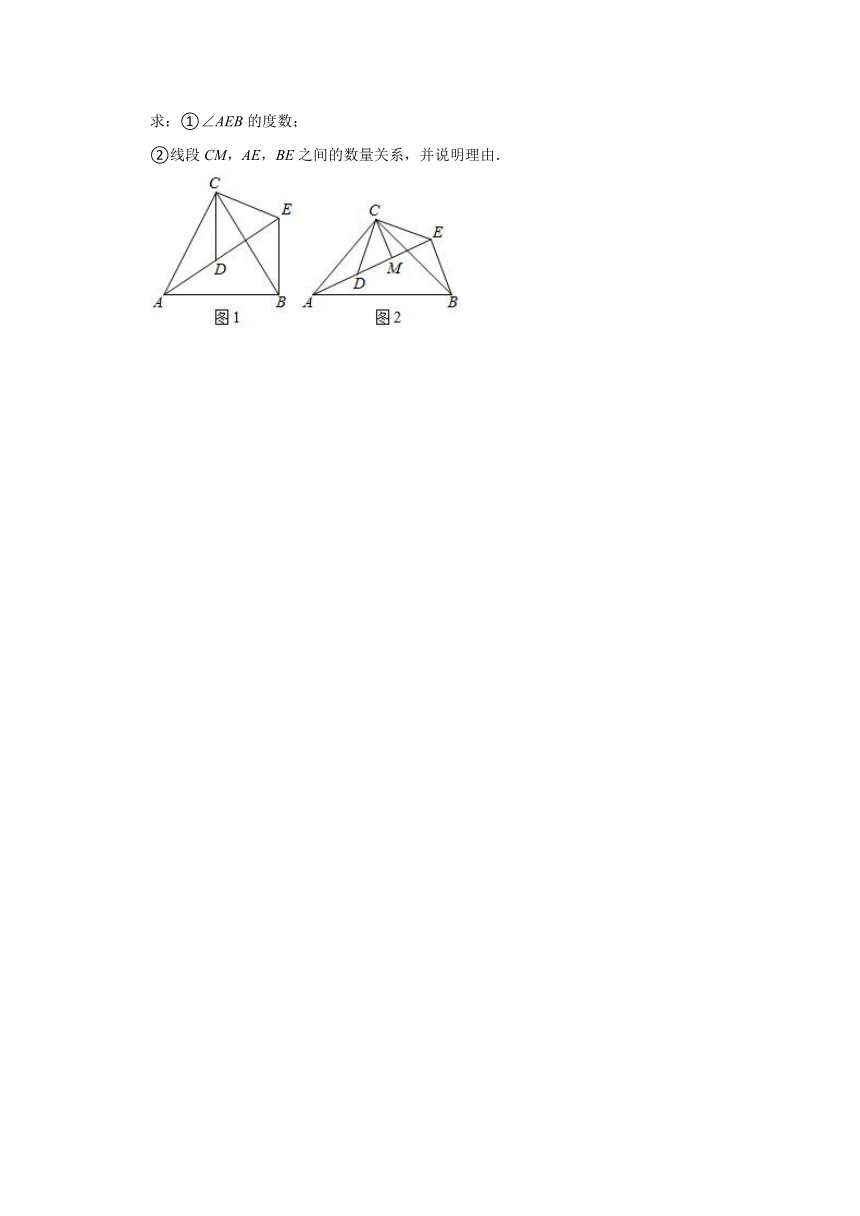
求:①∠AEB的度数;
②线段CM,AE,BE之间的数量关系,并说明理由.
2020-2021学年上海市浦东新区第四教育署七年级(下)调研数学试卷(5月份)
参考答案与试题解析
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.(2分)在下列实数中,无理数是( )
A.3 B. C.0 D.﹣
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:A.3是整数,属于有理数,故本选项不合题意;
B.是无理数,故本选项符合题意;
C.0是整数,属于有理数,故本选项不合题意;
D.﹣是分数,属于有理数,故本选项不合题意;
故选:B.
2.(2分)下列各式中,计算正确的是( )
A.×= B.=﹣2 C.=3 D.﹣=
【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.
【解答】解:=,故选项A正确;
==2,故选项B错误;
=3,故选项C错误;
与不是同类二次根式,不能合并,故选项D错误;
故选:A.
3.(2分)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
【分析】首先根据三角形的三边关系定理,求得第三边的取值范围,再进一步找到符合条件的数值.
【解答】解:设这个三角形的第三边为x.
根据三角形的三边关系定理,得:9﹣4<x<9+4,
解得5<x<13.
故选:D.
4.(2分)如果∠A=∠B﹣∠C,那么△ABC是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
【分析】由三角形内角和是180°,即∠A+∠B+C=180°代入即可.
【解答】解:因为∠A+∠B+C=180°,
且∠A=∠B﹣∠C,
所以∠B﹣∠C+∠B+C=180°,
所以∠B=90°,
所以△ABC是直角三角形.
故选:C.
5.(2分)下列说法中,正确的个数是( )
①在同一平面内,不相交的两条直线一定平行;
②过一点有且只有一条直线与已知直线平行;
③两条平行线被第三条直线所截,一对内错角的角平分线互相平行;
④从直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
A.1个 B.2个 C.3个 D.4个
【分析】本题可结合平行线的定义,平行公理,平行线的性质,点到直线的距离的定义进行判定即可.
【解答】解:①在同一平面内不相交的两条直线一定平行,故此说法正确;
②在同一平面内经过一点有且只有一条直线与已知直线平行,故此说法错误;
③两条平行线被第三条直线所截,一对内错角的角平分线互相平行,故此说法正确.
④从直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离,故此说法错误.
故选:B.
6.(2分)如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
【分析】由AB=BC得出∠A=∠C,根据三角形外角的性质和直角三角形锐角互余,即可得到α﹣∠A=β,α+∠C=90°,两式相加即可得出2α=90°+β,从而求得2α﹣β=90°.
【解答】解:∵AB=BC,
∴∠A=∠C,
∵α﹣∠A=β,α+∠C=90°,
∴2α=90°+β,
∴2α﹣β=90°,
故选:D.
二、填空题(本大题共有12小题,每题3分,共36分)
7.(3分)把化成幂的形式是 .
【分析】根据分数指数幂的意义可直接进行转化.
【解答】解:=.
故答案为:.
8.(3分)若x3=﹣,则x的值为 .
【分析】如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根,这就是说,如果x3=a,那么x叫做a的立方根.
【解答】解:∵,
∴x的值为.
故答案为:.
9.(3分)计算:(﹣3)﹣1+×= .
【分析】先算负整数指数幂,二次根式的乘法,再算加法即可求解.
【解答】解:(﹣3)﹣1+×
=﹣+4
=.
故答案为:.
10.(3分)若与|2x+y﹣6|互为相反数,则(x+y)2的平方根是 ±5 .
【分析】根据互为相反数的两个数的和等于0列方程,再根据非负数的性质列方程求出x、y的值,然后代入代数式求解,再根据平方根的定义解答.
【解答】解:∵与|2x+y﹣6|互为相反数,
∴+|2x+y﹣6|=0,
∴,
解得,
∴(x+y)2=(1+4)2=25,
∴(x+y)2的平方根是±5.
故答案为:±5.
11.(3分)近似数0.730的有效数字有 3 个.
【分析】一个近似数的有效数字是从左边第一个不是0的数字起,后面所有的数字都是这个数的有效数字.
【解答】解:0.730有7,3,0,三个有效数字.
故答案为:3.
12.(3分)如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为 15 度.
【分析】利用图中角与角的关系即可求得,即∠COF=∠DOE=90°﹣∠BOD.
【解答】解:∵直线FE⊥AB于O,
∴∠BOE=90°,
∵∠DOE=∠BOE﹣∠BOD,∠BOD=75°,
∴∠DOE=15°,
∴∠COF=∠DOE=15°.
故答案为:15.
13.(3分)如图,∠E的同位角有 2 个.
【分析】根据同位角的定义解答即可.
【解答】解:根据同位角的定义可得:∠BAD和∠E是同位角;∠BAC和∠E是同位角;
∴∠E的同位角有2个.
故答案为:2.
14.(3分)如图,∠1=115°,∠2=50°,那么∠3= 65° .
【分析】三角形一个外角等于不相邻的两个内角的和即可得出答案.
【解答】解:∵∠1=115°,∠2=50°,
∴∠3=∠1﹣∠2=65°,
故答案为:65°.
15.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= 35 °.
【分析】根据角平分线的定义得出∠CBP=∠ABP=15°,∠PCM=∠ACP=50°,根据三角形的外角性质得出∠P=∠PCM﹣∠CBP,再求出答案即可.
【解答】解:∵BP是△ABC中∠ABC的平分线,∠ABP=15°,
∴∠CBP=∠ABP=15°,
∵CP是∠ACB的外角的平分线,∠ACP=50°,
∴∠PCM=∠ACP=50°,
∴∠P=∠PCM﹣∠CBP=50°﹣15°=35°,
故答案为:35.
16.(3分)如图,已知△ABC≌△ABD,且点C与点D对应,点A与点A对应,∠ACB=30°,∠ABC=85°,则∠BAD的度数为 65° .
【分析】先根据三角形的内角和定理求出∠BAC,再根据全等三角形的性质求出∠BAD即可.
【解答】解:在△ABC中,
∵∠ACB=30°,∠ABC=85°,∠BAC+∠ACB+∠ABC=180°,
∴∠BAC=180°﹣∠ACB+∠ABC=65°,
∵△ABC≌△ABD,且点C与点D对应,点A与点A对应,
∴∠BAD=∠BAC=65°,
故答案为65°.
17.(3分)如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF= 3 .
【分析】根据全等三角形的性质证得BC=EF,再根据线段的和差即可求得CF,
【解答】解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
18.(3分)如图,若AB,CD相交于点E,若△ABC≌△ADE,且点B与点D对应,点C与点E对应,∠BAC=28°,则∠B的度数是 48 °.
【分析】由全等三角形的性质得到∠B=∠D,AC=AE,∠BAC=∠BAD,由等腰三角形的性质和三角形内角和定理求出∠ACE,再根据三角形内角和定理求出∠D,即可得到∠B的度数.
【解答】解:∵△ABC≌△ADE,且点B与点D对应,点C与点E对应,
∴∠B=∠D,AC=AE,∠BAC=∠BAD,
∴∠ACE=∠AEC,
∵∠ACE+∠AEC+∠BAC=180°,∠BAC=28°,
∴∠ACE=∠AEC=(180°﹣∠BAC)=76°,∠BAD=28°,
∵∠D+∠CAD+∠ACE=180°,
∴∠D=180°﹣∠CAD﹣∠ACE=48°,
故答案为48.
三、解答题(本大题共8小题,第19、20题每题5分,第21至24分每题6分,第25题8分,第26题10分,共52分)
19.(5分)计算:.
【分析】从左向右计算即可.
【解答】解:原式===24.
20.(5分)计算:﹣12021﹣+(π﹣3.14)0﹣(﹣)﹣2.
【分析】本题涉及乘方、零指数幂、负整数指数幂、三次根式化简4个知识点.在计算时,需要针对每个知识点分别进行计算,然后根据实数的运算法则求得计算结果.
【解答】解:﹣12021﹣+(π﹣3.14)0﹣(﹣)﹣2.
=﹣1﹣2+1﹣4
=﹣6.
21.(6分)利用幂的运算性质进行计算:×÷×8.
【分析】直接利用分数指数幂的性质化简,进而计算得出答案.
【解答】解:原式=16×2÷4×8
=2×2÷2×2
=2
=22
=4.
22.(6分)如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB ( 已知 ),
所以∠1+ ∠DEA =180° ( 两直线平行同旁内角互补 ).
因为∠1=∠A(已知),
所以∠A+ ∠DEA =180° ( 等量代换 ).
所以DE∥AC ( 同旁内角互补两直线平行 ).
【分析】根据平行线的判定、等量代换及平行线的判定逐一求解即可.
【解答】解:因为DF∥AB (已知),
所以∠1+∠DEA=180° (两直线平行同旁内角互补).
因为∠1=∠A(已知),
所以∠A+∠DEA=180° (等量代换).
所以DE∥AC (同旁内角互补两直线平行).
故答案为:已知,∠DEA,两直线平行同旁内角互补,∠DEA,等量代换,同旁内角互补两直线平行.
23.(6分)如图,FA⊥EC,垂足为E,∠F=40°,∠C=20°,求∠FBC的度数.
【分析】根据三角形的内角和可得∠A的度数,再利用外角的性质可得∠FBC的度数.
【解答】解:在△AEC 中,FA⊥EC,
∴∠AEC=90°,
∴∠A=90°﹣∠C=70°.
∴∠FBC=∠A+∠F=70°+40°=110°.
24.(6分)如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,试说明FG与BC的位置关系.
【分析】易得DE∥CF,推出∠1=∠2=∠BCF,根据平行线的判定推出即可.
【解答】解:FG∥BC,
理由是:∵CF⊥AB,ED⊥AB,
∴DE∥CF,
∴∠1=∠BCF,
∵∠1=∠2,
∴∠2=∠BCF,
∴FG∥BC.
25.(8分)如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.
(1)求证:△ABD≌△ACE.
(2)若∠ADE=2∠B,BD=2,求AE的长.
【分析】(1)根据等腰三角形等边对等角的性质可以得到∠B=∠C,然后根据SAS证明△ABD和△ACE全等即可;
(2)证得∠B=∠BAD,得出BD=AD=2,由全等三角形的性质可得出答案.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠ADE=2∠B,
∴∠B=∠BAD,
∴BD=AD=2,
∵△ABD≌△ACE,
∴AE=AD=2.
26.(10分)(1)问题发现
如图1,已知△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE;
求:①∠AEB的度数;
②线段CM,AE,BE之间的数量关系,并说明理由.
【分析】(1)先判断出CA=CB,CD=CE,∠ACB=∠DCE=60°,进而得出∠ACD=∠BCE,进而用SAS判断出△ACD≌△BCE,得出∠ADC=∠BEC,即可得出结论;
(2)①同(1)的方法,即可得出结论;
②同(1)的方法得,△ACD≌△BCE(SAS)得出AD=BE,再判断出DM=CM,即可得出结论.
【解答】解:(1)∵△ACB和△DCE是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠DCE﹣∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△CD≌△BCE(SAS),
∴∠ADC=∠BEC,
∵△CDE是等边三角形,
∴∠CDE=∠CED=60°,
∴∠ADC=180°﹣∠CDE=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°;
(2)①同(1)的方法得,△ACD≌△BCE(SAS),
∴∠ADC=∠BEC,
∵△DCE是等腰直角三角形,
∴∠CDE=∠CED=45°,
∴∠ADC=180°﹣∠CDE=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°;
②同(1)的方法得,△ACD≌△BCE(SAS),
∴AD=BE,
∵CD=CE,CM⊥DE,
∴DM=ME,
在Rt△DCE中,CM⊥DE,∠CDM=45°,
∴∠DCM=∠CDM=45°,
∴DM=CM,
∴DM=ME=CM,
∴AE=AD+DE=BE+2CM.
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.(2分)在下列实数中,无理数是( )
A.3 B. C.0 D.﹣
2.(2分)下列各式中,计算正确的是( )
A.×= B.=﹣2 C.=3 D.﹣=
3.(2分)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
4.(2分)如果∠A=∠B﹣∠C,那么△ABC是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
5.(2分)下列说法中,正确的个数是( )
①在同一平面内,不相交的两条直线一定平行;
②过一点有且只有一条直线与已知直线平行;
③两条平行线被第三条直线所截,一对内错角的角平分线互相平行;
④从直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
A.1个 B.2个 C.3个 D.4个
6.(2分)如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
二、填空题(本大题共有12小题,每题3分,共36分)
7.(3分)把化成幂的形式是 .
8.(3分)若x3=﹣,则x的值为 .
9.(3分)计算:(﹣3)﹣1+×= .
10.(3分)若与|2x+y﹣6|互为相反数,则(x+y)2的平方根是 .
11.(3分)近似数0.730的有效数字有 个.
12.(3分)如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为 度.
13.(3分)如图,∠E的同位角有 个.
14.(3分)如图,∠1=115°,∠2=50°,那么∠3= .
15.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= °.
16.(3分)如图,已知△ABC≌△ABD,且点C与点D对应,点A与点A对应,∠ACB=30°,∠ABC=85°,则∠BAD的度数为 .
17.(3分)如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF= .
18.(3分)如图,若AB,CD相交于点E,若△ABC≌△ADE,且点B与点D对应,点C与点E对应,∠BAC=28°,则∠B的度数是 °.
三、解答题(本大题共8小题,第19、20题每题5分,第21至24分每题6分,第25题8分,第26题10分,共52分)
19.(5分)计算:.
20.(5分)计算:﹣12021﹣+(π﹣3.14)0﹣(﹣)﹣2.
21.(6分)利用幂的运算性质进行计算:×÷×8.
22.(6分)如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB ( ),
所以∠1+ =180° ( ).
因为∠1=∠A(已知),
所以∠A+ =180° ( ).
所以DE∥AC ( ).
23.(6分)如图,FA⊥EC,垂足为E,∠F=40°,∠C=20°,求∠FBC的度数.
24.(6分)如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,试说明FG与BC的位置关系.
25.(8分)如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.
(1)求证:△ABD≌△ACE.
(2)若∠ADE=2∠B,BD=2,求AE的长.
26.(10分)(1)问题发现
如图1,已知△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE;
求:①∠AEB的度数;
②线段CM,AE,BE之间的数量关系,并说明理由.
2020-2021学年上海市浦东新区第四教育署七年级(下)调研数学试卷(5月份)
参考答案与试题解析
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.(2分)在下列实数中,无理数是( )
A.3 B. C.0 D.﹣
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】解:A.3是整数,属于有理数,故本选项不合题意;
B.是无理数,故本选项符合题意;
C.0是整数,属于有理数,故本选项不合题意;
D.﹣是分数,属于有理数,故本选项不合题意;
故选:B.
2.(2分)下列各式中,计算正确的是( )
A.×= B.=﹣2 C.=3 D.﹣=
【分析】根据各个选项中的式子,可以计算出正确的结果,从而可以解答本题.
【解答】解:=,故选项A正确;
==2,故选项B错误;
=3,故选项C错误;
与不是同类二次根式,不能合并,故选项D错误;
故选:A.
3.(2分)已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2 B.3 C.4 D.9
【分析】首先根据三角形的三边关系定理,求得第三边的取值范围,再进一步找到符合条件的数值.
【解答】解:设这个三角形的第三边为x.
根据三角形的三边关系定理,得:9﹣4<x<9+4,
解得5<x<13.
故选:D.
4.(2分)如果∠A=∠B﹣∠C,那么△ABC是( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
【分析】由三角形内角和是180°,即∠A+∠B+C=180°代入即可.
【解答】解:因为∠A+∠B+C=180°,
且∠A=∠B﹣∠C,
所以∠B﹣∠C+∠B+C=180°,
所以∠B=90°,
所以△ABC是直角三角形.
故选:C.
5.(2分)下列说法中,正确的个数是( )
①在同一平面内,不相交的两条直线一定平行;
②过一点有且只有一条直线与已知直线平行;
③两条平行线被第三条直线所截,一对内错角的角平分线互相平行;
④从直线外一点到这条直线的垂线段,叫做这个点到直线的距离;
A.1个 B.2个 C.3个 D.4个
【分析】本题可结合平行线的定义,平行公理,平行线的性质,点到直线的距离的定义进行判定即可.
【解答】解:①在同一平面内不相交的两条直线一定平行,故此说法正确;
②在同一平面内经过一点有且只有一条直线与已知直线平行,故此说法错误;
③两条平行线被第三条直线所截,一对内错角的角平分线互相平行,故此说法正确.
④从直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离,故此说法错误.
故选:B.
6.(2分)如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
【分析】由AB=BC得出∠A=∠C,根据三角形外角的性质和直角三角形锐角互余,即可得到α﹣∠A=β,α+∠C=90°,两式相加即可得出2α=90°+β,从而求得2α﹣β=90°.
【解答】解:∵AB=BC,
∴∠A=∠C,
∵α﹣∠A=β,α+∠C=90°,
∴2α=90°+β,
∴2α﹣β=90°,
故选:D.
二、填空题(本大题共有12小题,每题3分,共36分)
7.(3分)把化成幂的形式是 .
【分析】根据分数指数幂的意义可直接进行转化.
【解答】解:=.
故答案为:.
8.(3分)若x3=﹣,则x的值为 .
【分析】如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根,这就是说,如果x3=a,那么x叫做a的立方根.
【解答】解:∵,
∴x的值为.
故答案为:.
9.(3分)计算:(﹣3)﹣1+×= .
【分析】先算负整数指数幂,二次根式的乘法,再算加法即可求解.
【解答】解:(﹣3)﹣1+×
=﹣+4
=.
故答案为:.
10.(3分)若与|2x+y﹣6|互为相反数,则(x+y)2的平方根是 ±5 .
【分析】根据互为相反数的两个数的和等于0列方程,再根据非负数的性质列方程求出x、y的值,然后代入代数式求解,再根据平方根的定义解答.
【解答】解:∵与|2x+y﹣6|互为相反数,
∴+|2x+y﹣6|=0,
∴,
解得,
∴(x+y)2=(1+4)2=25,
∴(x+y)2的平方根是±5.
故答案为:±5.
11.(3分)近似数0.730的有效数字有 3 个.
【分析】一个近似数的有效数字是从左边第一个不是0的数字起,后面所有的数字都是这个数的有效数字.
【解答】解:0.730有7,3,0,三个有效数字.
故答案为:3.
12.(3分)如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为 15 度.
【分析】利用图中角与角的关系即可求得,即∠COF=∠DOE=90°﹣∠BOD.
【解答】解:∵直线FE⊥AB于O,
∴∠BOE=90°,
∵∠DOE=∠BOE﹣∠BOD,∠BOD=75°,
∴∠DOE=15°,
∴∠COF=∠DOE=15°.
故答案为:15.
13.(3分)如图,∠E的同位角有 2 个.
【分析】根据同位角的定义解答即可.
【解答】解:根据同位角的定义可得:∠BAD和∠E是同位角;∠BAC和∠E是同位角;
∴∠E的同位角有2个.
故答案为:2.
14.(3分)如图,∠1=115°,∠2=50°,那么∠3= 65° .
【分析】三角形一个外角等于不相邻的两个内角的和即可得出答案.
【解答】解:∵∠1=115°,∠2=50°,
∴∠3=∠1﹣∠2=65°,
故答案为:65°.
15.(3分)如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= 35 °.
【分析】根据角平分线的定义得出∠CBP=∠ABP=15°,∠PCM=∠ACP=50°,根据三角形的外角性质得出∠P=∠PCM﹣∠CBP,再求出答案即可.
【解答】解:∵BP是△ABC中∠ABC的平分线,∠ABP=15°,
∴∠CBP=∠ABP=15°,
∵CP是∠ACB的外角的平分线,∠ACP=50°,
∴∠PCM=∠ACP=50°,
∴∠P=∠PCM﹣∠CBP=50°﹣15°=35°,
故答案为:35.
16.(3分)如图,已知△ABC≌△ABD,且点C与点D对应,点A与点A对应,∠ACB=30°,∠ABC=85°,则∠BAD的度数为 65° .
【分析】先根据三角形的内角和定理求出∠BAC,再根据全等三角形的性质求出∠BAD即可.
【解答】解:在△ABC中,
∵∠ACB=30°,∠ABC=85°,∠BAC+∠ACB+∠ABC=180°,
∴∠BAC=180°﹣∠ACB+∠ABC=65°,
∵△ABC≌△ABD,且点C与点D对应,点A与点A对应,
∴∠BAD=∠BAC=65°,
故答案为65°.
17.(3分)如图,已知△ABC≌△DEF,且点B与点E对应,点C与点F对应,BE=5,BF=1,则CF= 3 .
【分析】根据全等三角形的性质证得BC=EF,再根据线段的和差即可求得CF,
【解答】解:∵△ABC≌△DEF,且点B与点E对应,点C与点F对应,
∴BC=EF,
∵BE=5,BF=1,
∴EF=BE﹣BF=4,
∴BC=4,
∴CF=BC﹣BF=4﹣1=3,
故答案为3.
18.(3分)如图,若AB,CD相交于点E,若△ABC≌△ADE,且点B与点D对应,点C与点E对应,∠BAC=28°,则∠B的度数是 48 °.
【分析】由全等三角形的性质得到∠B=∠D,AC=AE,∠BAC=∠BAD,由等腰三角形的性质和三角形内角和定理求出∠ACE,再根据三角形内角和定理求出∠D,即可得到∠B的度数.
【解答】解:∵△ABC≌△ADE,且点B与点D对应,点C与点E对应,
∴∠B=∠D,AC=AE,∠BAC=∠BAD,
∴∠ACE=∠AEC,
∵∠ACE+∠AEC+∠BAC=180°,∠BAC=28°,
∴∠ACE=∠AEC=(180°﹣∠BAC)=76°,∠BAD=28°,
∵∠D+∠CAD+∠ACE=180°,
∴∠D=180°﹣∠CAD﹣∠ACE=48°,
故答案为48.
三、解答题(本大题共8小题,第19、20题每题5分,第21至24分每题6分,第25题8分,第26题10分,共52分)
19.(5分)计算:.
【分析】从左向右计算即可.
【解答】解:原式===24.
20.(5分)计算:﹣12021﹣+(π﹣3.14)0﹣(﹣)﹣2.
【分析】本题涉及乘方、零指数幂、负整数指数幂、三次根式化简4个知识点.在计算时,需要针对每个知识点分别进行计算,然后根据实数的运算法则求得计算结果.
【解答】解:﹣12021﹣+(π﹣3.14)0﹣(﹣)﹣2.
=﹣1﹣2+1﹣4
=﹣6.
21.(6分)利用幂的运算性质进行计算:×÷×8.
【分析】直接利用分数指数幂的性质化简,进而计算得出答案.
【解答】解:原式=16×2÷4×8
=2×2÷2×2
=2
=22
=4.
22.(6分)如图,已知在△ABC中,点D、E、F分别在边BC、AB、AC上,且DF∥AB,∠1=∠A,试说明DE∥AC的理由.
解:因为DF∥AB ( 已知 ),
所以∠1+ ∠DEA =180° ( 两直线平行同旁内角互补 ).
因为∠1=∠A(已知),
所以∠A+ ∠DEA =180° ( 等量代换 ).
所以DE∥AC ( 同旁内角互补两直线平行 ).
【分析】根据平行线的判定、等量代换及平行线的判定逐一求解即可.
【解答】解:因为DF∥AB (已知),
所以∠1+∠DEA=180° (两直线平行同旁内角互补).
因为∠1=∠A(已知),
所以∠A+∠DEA=180° (等量代换).
所以DE∥AC (同旁内角互补两直线平行).
故答案为:已知,∠DEA,两直线平行同旁内角互补,∠DEA,等量代换,同旁内角互补两直线平行.
23.(6分)如图,FA⊥EC,垂足为E,∠F=40°,∠C=20°,求∠FBC的度数.
【分析】根据三角形的内角和可得∠A的度数,再利用外角的性质可得∠FBC的度数.
【解答】解:在△AEC 中,FA⊥EC,
∴∠AEC=90°,
∴∠A=90°﹣∠C=70°.
∴∠FBC=∠A+∠F=70°+40°=110°.
24.(6分)如图,已知CF⊥AB于F,ED⊥AB于D,∠1=∠2,试说明FG与BC的位置关系.
【分析】易得DE∥CF,推出∠1=∠2=∠BCF,根据平行线的判定推出即可.
【解答】解:FG∥BC,
理由是:∵CF⊥AB,ED⊥AB,
∴DE∥CF,
∴∠1=∠BCF,
∵∠1=∠2,
∴∠2=∠BCF,
∴FG∥BC.
25.(8分)如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.
(1)求证:△ABD≌△ACE.
(2)若∠ADE=2∠B,BD=2,求AE的长.
【分析】(1)根据等腰三角形等边对等角的性质可以得到∠B=∠C,然后根据SAS证明△ABD和△ACE全等即可;
(2)证得∠B=∠BAD,得出BD=AD=2,由全等三角形的性质可得出答案.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠ADE=2∠B,
∴∠B=∠BAD,
∴BD=AD=2,
∵△ABD≌△ACE,
∴AE=AD=2.
26.(10分)(1)问题发现
如图1,已知△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.
(2)拓展探究
如图2,若△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE;
求:①∠AEB的度数;
②线段CM,AE,BE之间的数量关系,并说明理由.
【分析】(1)先判断出CA=CB,CD=CE,∠ACB=∠DCE=60°,进而得出∠ACD=∠BCE,进而用SAS判断出△ACD≌△BCE,得出∠ADC=∠BEC,即可得出结论;
(2)①同(1)的方法,即可得出结论;
②同(1)的方法得,△ACD≌△BCE(SAS)得出AD=BE,再判断出DM=CM,即可得出结论.
【解答】解:(1)∵△ACB和△DCE是等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°,
∴∠BCD=∠DCE﹣∠BCD,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△CD≌△BCE(SAS),
∴∠ADC=∠BEC,
∵△CDE是等边三角形,
∴∠CDE=∠CED=60°,
∴∠ADC=180°﹣∠CDE=120°,
∴∠BEC=120°,
∴∠AEB=∠BEC﹣∠CED=120°﹣60°=60°;
(2)①同(1)的方法得,△ACD≌△BCE(SAS),
∴∠ADC=∠BEC,
∵△DCE是等腰直角三角形,
∴∠CDE=∠CED=45°,
∴∠ADC=180°﹣∠CDE=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC﹣∠CED=135°﹣45°=90°;
②同(1)的方法得,△ACD≌△BCE(SAS),
∴AD=BE,
∵CD=CE,CM⊥DE,
∴DM=ME,
在Rt△DCE中,CM⊥DE,∠CDM=45°,
∴∠DCM=∠CDM=45°,
∴DM=CM,
∴DM=ME=CM,
∴AE=AD+DE=BE+2CM.
同课章节目录
