矩形的性质第一课时
图片预览


文档简介
(共38张PPT)
矩形的性质
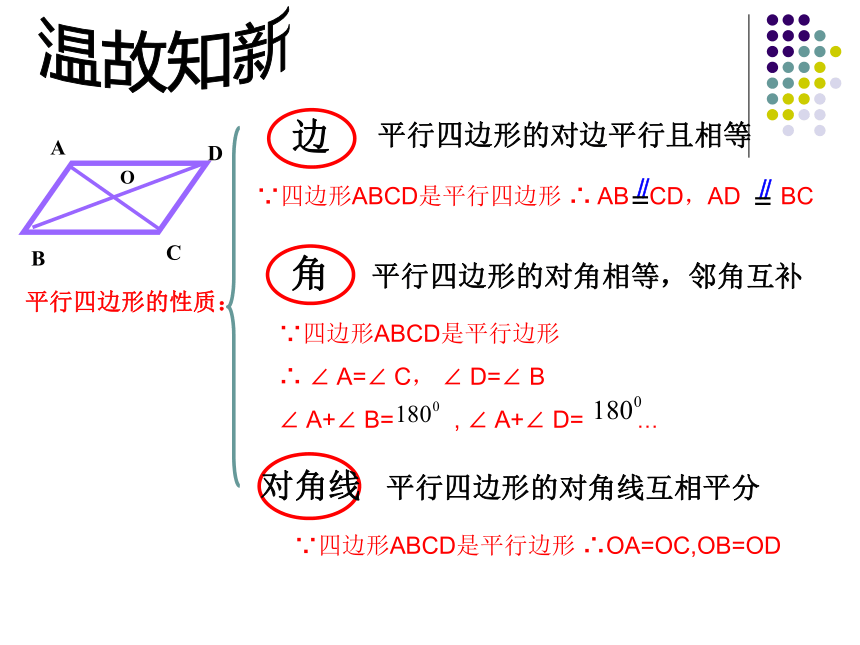
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形 ∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
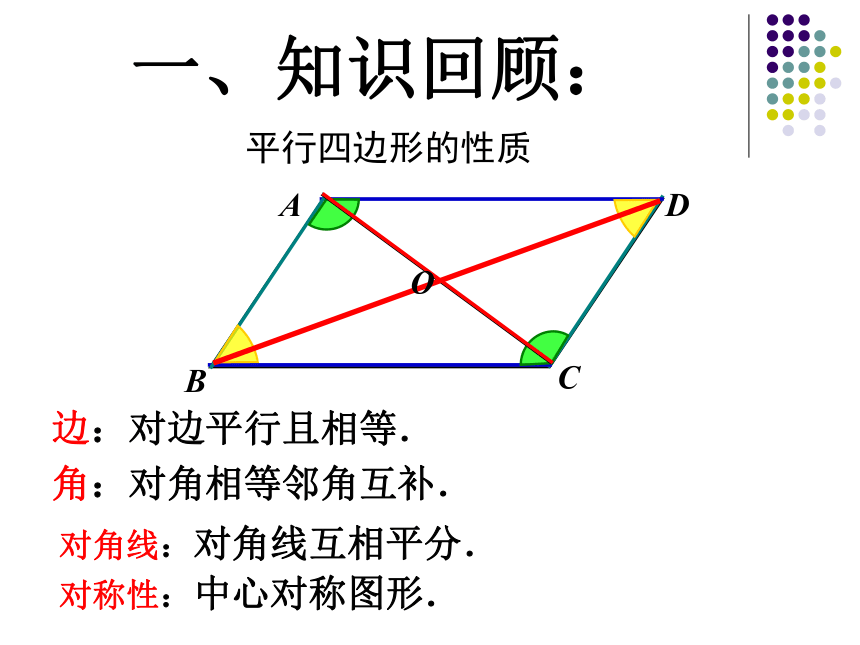
边:对边平行且相等.
角:对角相等邻角互补.
对角线:对角线互相平分.
平行四边形的性质
A
B
C
D
一、知识回顾:
O
对称性:中心对称图形.
生
活
中
的
矩
形
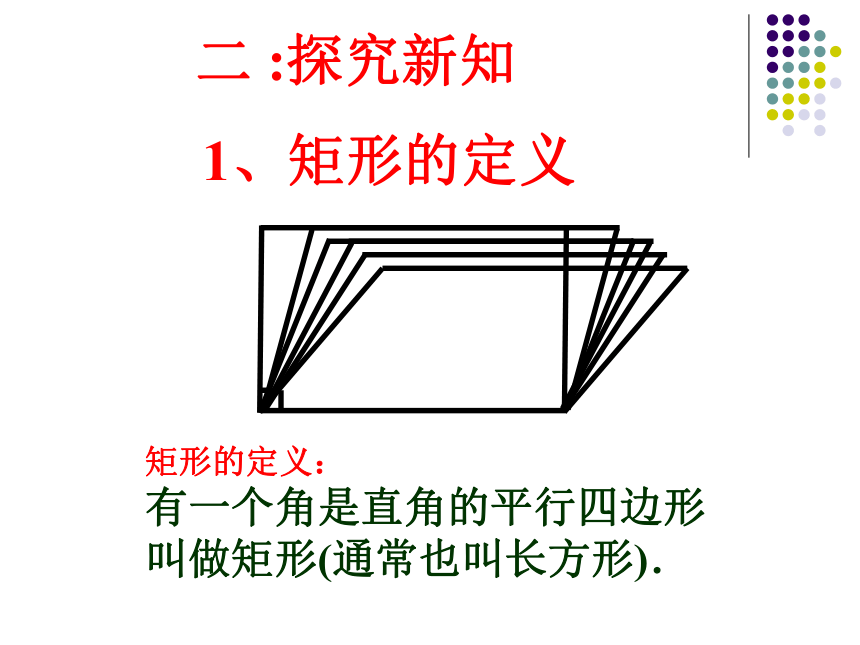
1、矩形的定义
矩形的定义:
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
二 :探究新知
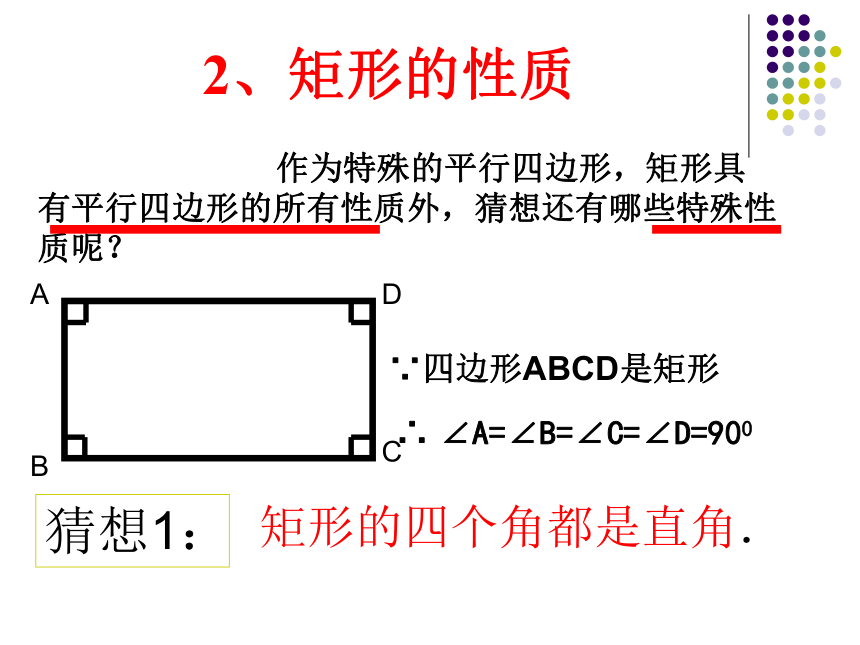
作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?
猜想1:
A
B
C
D
2、矩形的性质
矩形的四个角都是直角.
∴ ∠A=∠B=∠C=∠D=900
∵四边形ABCD是矩形
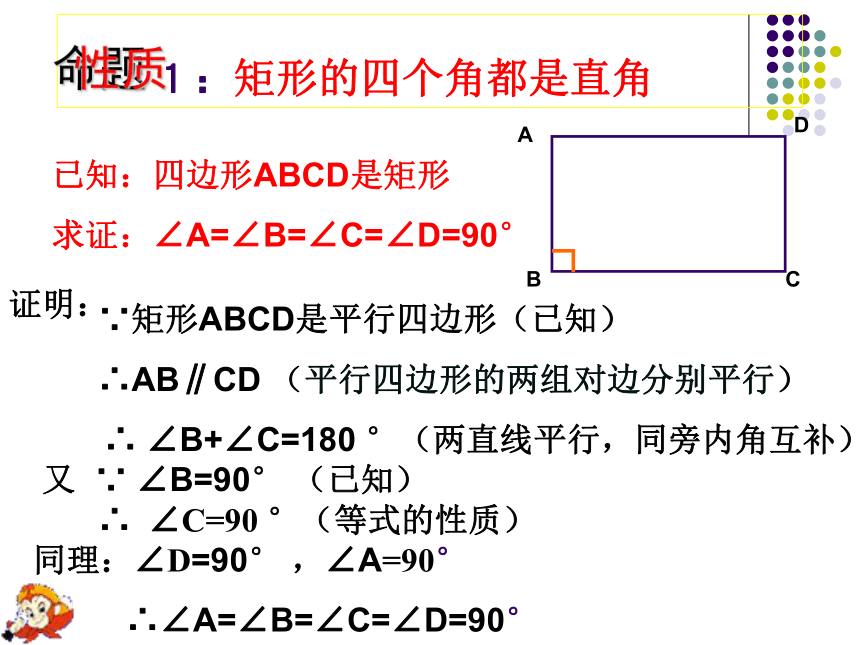
1:矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
∵矩形ABCD是平行四边形(已知)
∴AB∥CD (平行四边形的两组对边分别平行)
∴ ∠B+∠C=180 °(两直线平行,同旁内角互补)
又 ∵ ∠B=90° (已知)
∴ ∠C=90 °(等式的性质)
同理:∠D=90° ,∠A=90°
∴∠A=∠B=∠C=∠D=90°
命题
性质
证明:
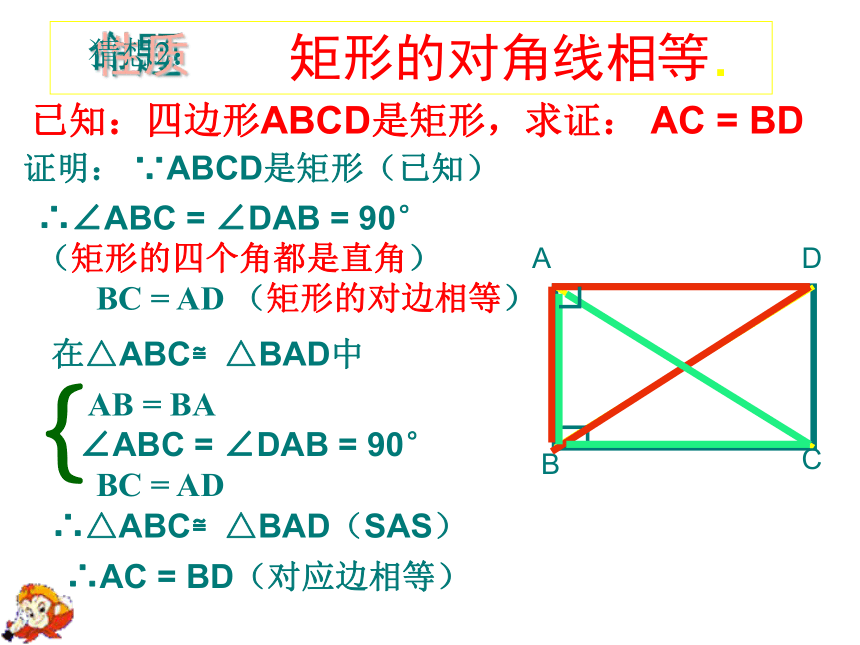
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明: ∵ABCD是矩形(已知)
∴∠ABC = ∠DAB = 90°
(矩形的四个角都是直角)
BC = AD (矩形的对边相等)
∴△ABC≌△BAD(SAS)
∴AC = BD(对应边相等)
2:矩形的对角线相等.
命题
性质
在△ABC≌△BAD中
AB = BA
∠ABC = ∠DAB = 90°
BC = AD
{
猜想2:
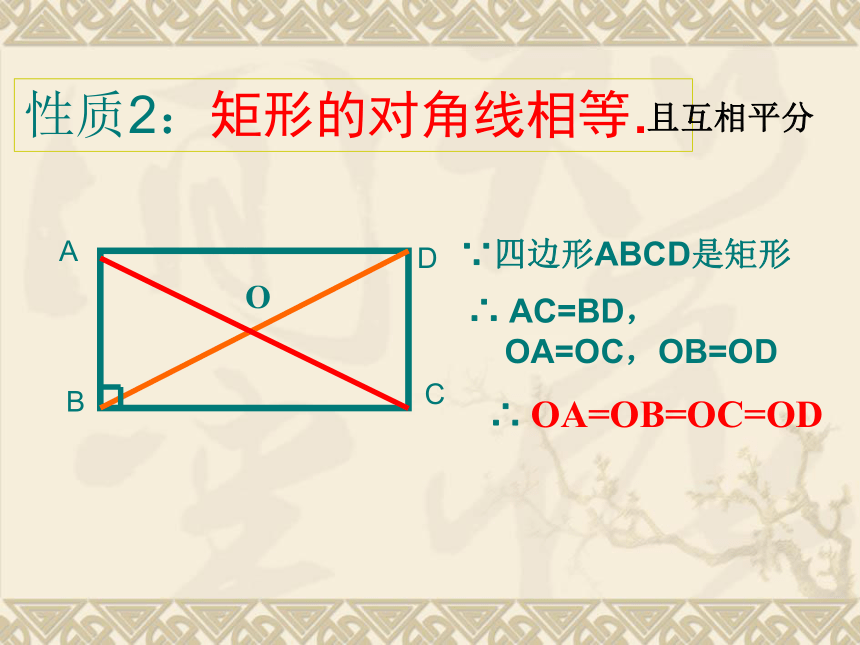
性质2:矩形的对角线相等.
A
B
C
D
∵四边形ABCD是矩形
∴ AC=BD,
OA=OC,OB=OD
∴ OA=OB=OC=OD
O
且互相平分
D
C
B
A
O
┛
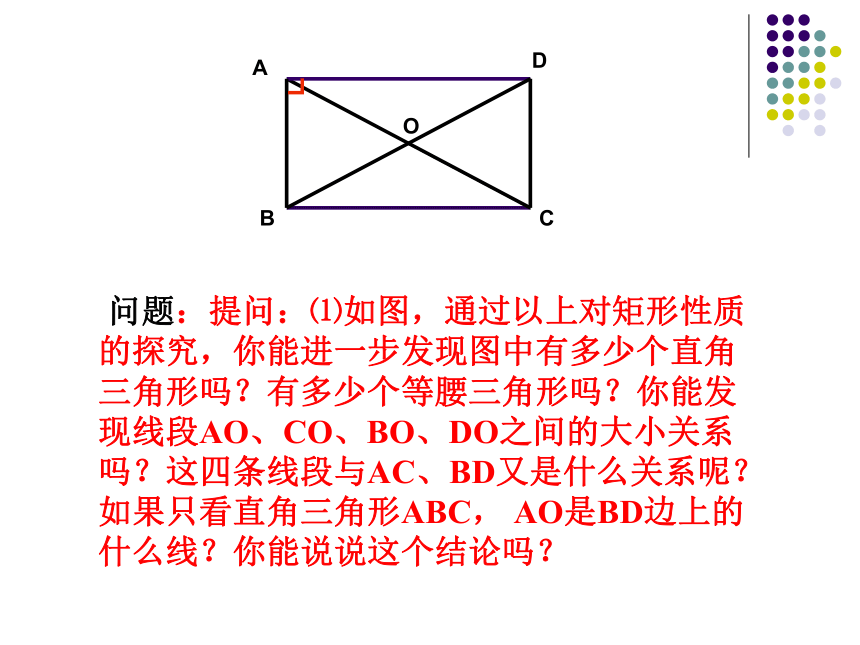
问题:提问:⑴如图,通过以上对矩形性质的探究,你能进一步发现图中有多少个直角三角形吗?有多少个等腰三角形吗?你能发现线段AO、CO、BO、DO之间的大小关系吗?这四条线段与AC、BD又是什么关系呢?如果只看直角三角形ABC, AO是BD边上的什么线?你能说说这个结论吗?
O
D
C
B
A
┛
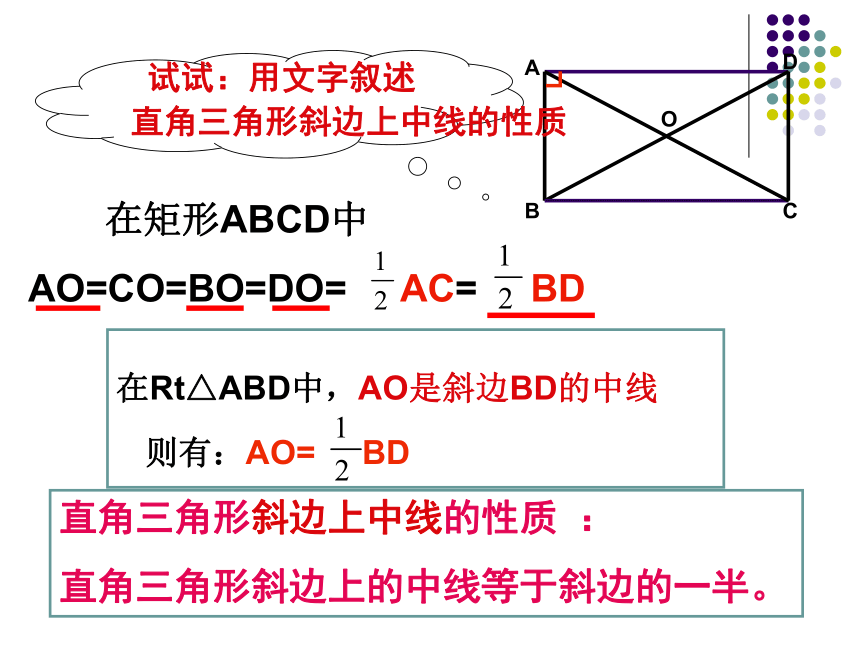
在Rt△ABD中,AO是斜边BD的中线
直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
试试:用文字叙述
直角三角形斜边上中线的性质
在矩形ABCD中
AO=CO=BO=DO= AC= BD
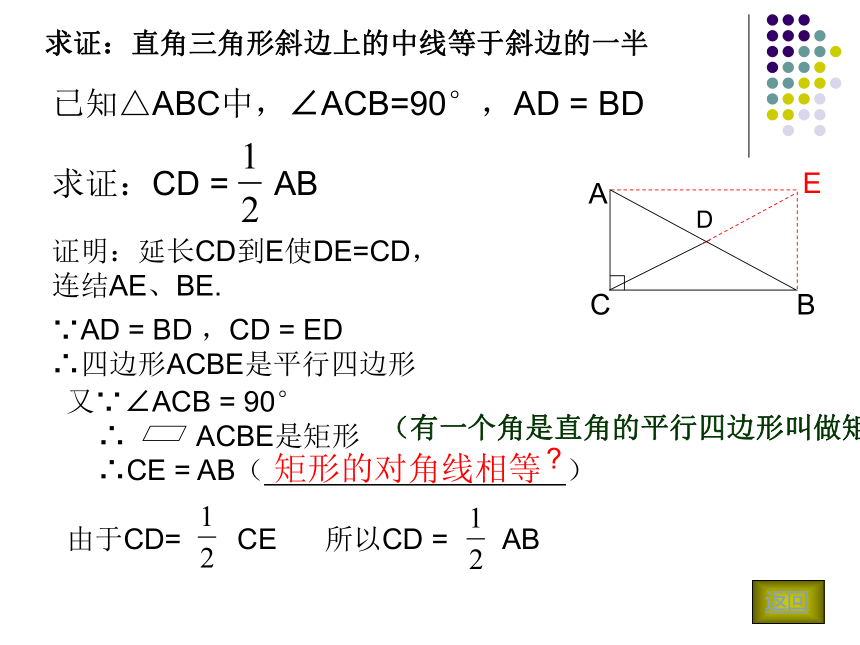
求证:直角三角形斜边上的中线等于斜边的一半
已知△ABC中,∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
A
B
C
D
∵AD = BD ,CD = ED
∴四边形ACBE是平行四边形
E
又∵∠ACB = 90°
∴ ACBE是矩形
∴CE = AB( )
由于CD= CE 所以CD = AB
返回
矩形的对角线相等
(有一个角是直角的平行四边形叫做矩形
例1 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
A
B
B
B
B
B
B
B
D
C
B
B
解:∵四边形ABCD是矩形
∴AC=BD,AO=1/2AC, BO=1/2BD
∴AO=BO
∵∠AOB=60°
∴△ABO是等边三角形∴AO=AB=BO=4
∴AC=BD=2×4=8cm
O
例2、如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
O
D
C
B
A
∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,
∴ AC=BD=13cm(矩形的对角线相等)
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm)
即矩形ABCD的周长等于34cm。
解:∵ 四边形ABCD是矩形
想一想:若△AOB的面积为5,则矩形ABCD的面积为_____
20
矩形的对称性:
O
中心对称图形
轴对称图形
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
矩形所特有的性质
练一练
1、下列性质中,矩形不一定具有的是( )
A.对角线相等 B. 四个角都相等
C.是轴对称图形 D.对角线垂直
D
2、如图,已知ABCD为矩形,若沿AE折叠,使D点落在BC边上F点处,如果∠BAF=600,那么∠DAE等于( )
A.150 B.300
C.450 D.600
A
F
E
D
C
B
A
4、如图,在矩形ABCD中,E是AB上的一点,EF⊥CE,交AD于点F,若BE=2,矩形的周长为16,CE=EF,则BC的长为_____
A
F
E
D
C
B
3
你能求出EF的长吗
3、如图,把两个完全相同的矩形拼成“L”形图案, 则∠FAC=______° ∠FCA=______°
G
A
B
D
E
C
F
90
45
⌒
⌒
⌒
⌒
1
2
3
4
2. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是
课堂练习
1. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形
3. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
[ ]
[ ]
D
D
D
A
返回
已知:如图,矩形ABCD的两条对角线相交于点O,
B
A
D
C
O
(1)若∠AOD=120°,判断△AOB的形状
(2)如果要得到 △AOB是等边三角形,你可以添加什么条件?
(3)在矩形ABCD中,AE⊥BD于E,若BE=OE=1,则AC=_____, AB=______∠AOB=__________
试一试:
4
2
60度
E
矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等
下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直
下面图形中,既是轴对称图形,又是中心对称图形的是( )
(A)角(B)任意三角形
(C)矩形(D)等腰三角形
由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)60度(B)45度
(C)30度(D)22.5度
根据题目要求算出结果并讲解理由。如图矩形ABCD中,1、AC=8cm,则BD=_____AO=___CO=___BO=____
2、AB=6 BC=8,则 AC= ___ AO=___BO=__
3、∠AOB=60° AB=4cm,则AC长______
说一说
A
O
C
D
B
8cm
4cm
4cm
4cm
10
5
5
8cm
3.矩形的边长为10cm和15cm,其中一个
内角的平分线分长边为两部分,这两部分
分别为 cm, cm.
A
B
C
D
E
返回
例3 已知:如左图,在矩形ABCD中,AB=3,BC=4,BE⊥AC于E。试求出BE的长。
B
A
D
C
E
解:在矩形ABCD中,∠ABC=900,
AC=√AB2+BC2= √32+42= √25=5(勾股定理)。
又∵S△ABC=1/2AB·BC=1/2AC·BE,
BE=AB·BC/AC=2.4
1.如图,在直角三角形ABC中,∠ACB=90°,BC=3,AC=4,D是AB的中点,则CD=———
A
C
B
D
2.5
2.已知矩形的对角线长为10cm,那么,顺次连接矩形四边中点所得的四边形周长( )cm
A.40 B.10 C.5 D.20
D
3、两条直角边的长分别为12和5,则斜边上的中线( )
(A)26 (B)13 (C)8.5 (D)6.5
A
B
C
D
思 路 分 析
2. 在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.
作斜边AB边的中线
则 AD=CD= AB
∴AC=AD=CD= AB
又∵AB=2AC
∴⊿ACD是等边三角形
∴∠A=60°
∴∠B=30 °
直角三角形中,如果一条直角边等于斜边的一半,
那么这个直角边所对的角为30 °
A
B
C
D
O
3. 矩形ABCD中,AB=1,
∠ACB=30°,BD=______;
与AB相等的线段(不包括本身)
有___条.
思 路 分 析
30°
在Rt⊿ABC中,
∠ACB=30 ° ,
∴AC=2AB
又∵AC=BD
∴BD=2AB=2
AB=AO=BO=OC=OD=CD
5
还有没有其他解法?
2
A
B
C
D
O
3. 矩形ABCD中,AB=1,
∠ACB=30°,BD=______;
与AB相等的线段(不包括本身)
有___条,
思 路 分 析
E
作BE⊥AC
在Rt⊿BCE中,
∠ACB=30°
BE= BC
而BC=
=
∴BE=
还有其他方法吗?
等面积!
B到AC边距离为____;
A
B
C
D
O
思路分析
⊿ABO是等边三角形,
AO=AB=
AC=2AO=
4. 矩形两条对角线夹角为60°,较短一边长 为 , 则此矩形对角线长为_______.
5. 以2cm和3cm为两条邻边长画一个矩形,并求它的对角线长.
思 路 分 析
A
B
C
①画AB=3cm,AC=2cm且AB⊥AC,
②作CD∥AB,
BD∥AC,
交于点D.
D
四边形ABCD就是所要画的矩形.
利用勾股定理求得BC
5、如果矩形的一条对角线的长为8 cm,两条对角线的一个交角为120°,求矩形的边长
6、如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
O
E
D
C
A
B
2.(补充)如图,在矩形ABCD中,对角线AC、BD相交于O,DE⊥AC于E,EC:AE=1:3,CD=5cm,求AC的长度。
A
B
C
D
E
O
从一般到特殊
边
角
对角线
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
直角三角形斜边上的中线性质
矩形的定义:
有一个角是直角的平行四边形叫做矩形
拓展延伸:
1、已知:矩形ABCD和点P,若PA=PD。
求证:PB=PC。
本题分三种情况思考:
A
A
A
B
B
B
C
C
C
D
D
D
P
P
P
点在形外
点在形上
点在形内
2、如图,把矩形ABCD放置平面直角坐标系中,
已知A(0,0)B(6,0)D(0,4),
求:(1)C点坐标;
(2)若直线y=kx-1将矩形ABCD分成面积相等的两部分,求此直线解析式 。
y
x
A
B
C
D
p
矩形的性质
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形 ∴ AB CD,AD BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD
边:对边平行且相等.
角:对角相等邻角互补.
对角线:对角线互相平分.
平行四边形的性质
A
B
C
D
一、知识回顾:
O
对称性:中心对称图形.
生
活
中
的
矩
形
1、矩形的定义
矩形的定义:
有一个角是直角的平行四边形叫做矩形(通常也叫长方形).
二 :探究新知
作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?
猜想1:
A
B
C
D
2、矩形的性质
矩形的四个角都是直角.
∴ ∠A=∠B=∠C=∠D=900
∵四边形ABCD是矩形
1:矩形的四个角都是直角
已知:四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
D
C
B
A
∵矩形ABCD是平行四边形(已知)
∴AB∥CD (平行四边形的两组对边分别平行)
∴ ∠B+∠C=180 °(两直线平行,同旁内角互补)
又 ∵ ∠B=90° (已知)
∴ ∠C=90 °(等式的性质)
同理:∠D=90° ,∠A=90°
∴∠A=∠B=∠C=∠D=90°
命题
性质
证明:
已知:四边形ABCD是矩形,求证: AC = BD
A
B
C
D
证明: ∵ABCD是矩形(已知)
∴∠ABC = ∠DAB = 90°
(矩形的四个角都是直角)
BC = AD (矩形的对边相等)
∴△ABC≌△BAD(SAS)
∴AC = BD(对应边相等)
2:矩形的对角线相等.
命题
性质
在△ABC≌△BAD中
AB = BA
∠ABC = ∠DAB = 90°
BC = AD
{
猜想2:
性质2:矩形的对角线相等.
A
B
C
D
∵四边形ABCD是矩形
∴ AC=BD,
OA=OC,OB=OD
∴ OA=OB=OC=OD
O
且互相平分
D
C
B
A
O
┛
问题:提问:⑴如图,通过以上对矩形性质的探究,你能进一步发现图中有多少个直角三角形吗?有多少个等腰三角形吗?你能发现线段AO、CO、BO、DO之间的大小关系吗?这四条线段与AC、BD又是什么关系呢?如果只看直角三角形ABC, AO是BD边上的什么线?你能说说这个结论吗?
O
D
C
B
A
┛
在Rt△ABD中,AO是斜边BD的中线
直角三角形斜边上中线的性质 :
直角三角形斜边上的中线等于斜边的一半。
则有:AO= BD
试试:用文字叙述
直角三角形斜边上中线的性质
在矩形ABCD中
AO=CO=BO=DO= AC= BD
求证:直角三角形斜边上的中线等于斜边的一半
已知△ABC中,∠ACB=90°,AD = BD
求证:CD = AB
证明:延长CD到E使DE=CD,
连结AE、BE.
A
B
C
D
∵AD = BD ,CD = ED
∴四边形ACBE是平行四边形
E
又∵∠ACB = 90°
∴ ACBE是矩形
∴CE = AB( )
由于CD= CE 所以CD = AB
返回
矩形的对角线相等
(有一个角是直角的平行四边形叫做矩形
例1 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
A
B
B
B
B
B
B
B
D
C
B
B
解:∵四边形ABCD是矩形
∴AC=BD,AO=1/2AC, BO=1/2BD
∴AO=BO
∵∠AOB=60°
∴△ABO是等边三角形∴AO=AB=BO=4
∴AC=BD=2×4=8cm
O
例2、如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长的和是86cm,对角线长是13cm,那么矩形的周长是多少?
O
D
C
B
A
∵ △AOB、 △BOC、 △COD和△AOD四个三角形的周长和为86cm,
∴ AC=BD=13cm(矩形的对角线相等)
∴ AB+BC+CD+DA=86-2(AC+BD)
=86-4×13
=34(cm)
即矩形ABCD的周长等于34cm。
解:∵ 四边形ABCD是矩形
想一想:若△AOB的面积为5,则矩形ABCD的面积为_____
20
矩形的对称性:
O
中心对称图形
轴对称图形
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
矩形所特有的性质
练一练
1、下列性质中,矩形不一定具有的是( )
A.对角线相等 B. 四个角都相等
C.是轴对称图形 D.对角线垂直
D
2、如图,已知ABCD为矩形,若沿AE折叠,使D点落在BC边上F点处,如果∠BAF=600,那么∠DAE等于( )
A.150 B.300
C.450 D.600
A
F
E
D
C
B
A
4、如图,在矩形ABCD中,E是AB上的一点,EF⊥CE,交AD于点F,若BE=2,矩形的周长为16,CE=EF,则BC的长为_____
A
F
E
D
C
B
3
你能求出EF的长吗
3、如图,把两个完全相同的矩形拼成“L”形图案, 则∠FAC=______° ∠FCA=______°
G
A
B
D
E
C
F
90
45
⌒
⌒
⌒
⌒
1
2
3
4
2. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是
课堂练习
1. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
A.对角线相等的四边形 B.对角线互相平分且相等的四边形
C.对角线互垂直平分的四边形 D.对角线垂直的四边形
3. 已知矩形的一条对角线与一边的夹角是40°,则两
条对角线所夹锐角的度数为
A.50° B.60° C.70° D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,
则∠BAE等于
A.30° B.45° C.60° D.120°
[ ]
[ ]
[ ]
[ ]
D
D
D
A
返回
已知:如图,矩形ABCD的两条对角线相交于点O,
B
A
D
C
O
(1)若∠AOD=120°,判断△AOB的形状
(2)如果要得到 △AOB是等边三角形,你可以添加什么条件?
(3)在矩形ABCD中,AE⊥BD于E,若BE=OE=1,则AC=_____, AB=______∠AOB=__________
试一试:
4
2
60度
E
矩形具有而平行四边形不具有的性质( )
(A)内角和是360度(B)对角相等
(C)对边平行且相等(D)对角线相等
下面性质中,矩形不一定具有的是( )
(A)对角线相等(B)四个角相等
(C)是轴对称图形(D)对角线垂直
下面图形中,既是轴对称图形,又是中心对称图形的是( )
(A)角(B)任意三角形
(C)矩形(D)等腰三角形
由已知矩形的一个顶点向其所对的对角线引垂线,该垂线分直角为3:1两部分,则垂线与另一条对角线的夹角是( )
(A)60度(B)45度
(C)30度(D)22.5度
根据题目要求算出结果并讲解理由。如图矩形ABCD中,1、AC=8cm,则BD=_____AO=___CO=___BO=____
2、AB=6 BC=8,则 AC= ___ AO=___BO=__
3、∠AOB=60° AB=4cm,则AC长______
说一说
A
O
C
D
B
8cm
4cm
4cm
4cm
10
5
5
8cm
3.矩形的边长为10cm和15cm,其中一个
内角的平分线分长边为两部分,这两部分
分别为 cm, cm.
A
B
C
D
E
返回
例3 已知:如左图,在矩形ABCD中,AB=3,BC=4,BE⊥AC于E。试求出BE的长。
B
A
D
C
E
解:在矩形ABCD中,∠ABC=900,
AC=√AB2+BC2= √32+42= √25=5(勾股定理)。
又∵S△ABC=1/2AB·BC=1/2AC·BE,
BE=AB·BC/AC=2.4
1.如图,在直角三角形ABC中,∠ACB=90°,BC=3,AC=4,D是AB的中点,则CD=———
A
C
B
D
2.5
2.已知矩形的对角线长为10cm,那么,顺次连接矩形四边中点所得的四边形周长( )cm
A.40 B.10 C.5 D.20
D
3、两条直角边的长分别为12和5,则斜边上的中线( )
(A)26 (B)13 (C)8.5 (D)6.5
A
B
C
D
思 路 分 析
2. 在Rt⊿ABC中,∠C=90°,
AB=2AC.
求∠ A 、 ∠B 的度数.
作斜边AB边的中线
则 AD=CD= AB
∴AC=AD=CD= AB
又∵AB=2AC
∴⊿ACD是等边三角形
∴∠A=60°
∴∠B=30 °
直角三角形中,如果一条直角边等于斜边的一半,
那么这个直角边所对的角为30 °
A
B
C
D
O
3. 矩形ABCD中,AB=1,
∠ACB=30°,BD=______;
与AB相等的线段(不包括本身)
有___条.
思 路 分 析
30°
在Rt⊿ABC中,
∠ACB=30 ° ,
∴AC=2AB
又∵AC=BD
∴BD=2AB=2
AB=AO=BO=OC=OD=CD
5
还有没有其他解法?
2
A
B
C
D
O
3. 矩形ABCD中,AB=1,
∠ACB=30°,BD=______;
与AB相等的线段(不包括本身)
有___条,
思 路 分 析
E
作BE⊥AC
在Rt⊿BCE中,
∠ACB=30°
BE= BC
而BC=
=
∴BE=
还有其他方法吗?
等面积!
B到AC边距离为____;
A
B
C
D
O
思路分析
⊿ABO是等边三角形,
AO=AB=
AC=2AO=
4. 矩形两条对角线夹角为60°,较短一边长 为 , 则此矩形对角线长为_______.
5. 以2cm和3cm为两条邻边长画一个矩形,并求它的对角线长.
思 路 分 析
A
B
C
①画AB=3cm,AC=2cm且AB⊥AC,
②作CD∥AB,
BD∥AC,
交于点D.
D
四边形ABCD就是所要画的矩形.
利用勾股定理求得BC
5、如果矩形的一条对角线的长为8 cm,两条对角线的一个交角为120°,求矩形的边长
6、如图:矩形ABCD的两条对角线
相交于点O,CE‖OB交AB的延长线
于点E,试证明AC与CE的大小关系。
O
E
D
C
A
B
2.(补充)如图,在矩形ABCD中,对角线AC、BD相交于O,DE⊥AC于E,EC:AE=1:3,CD=5cm,求AC的长度。
A
B
C
D
E
O
从一般到特殊
边
角
对角线
矩形对边平行且相等;
矩形的四个角都是直角;
矩形的对角线相等且平分;
直角三角形斜边上的中线等于斜边的一半.
A
B
C
D
直角三角形斜边上的中线性质
矩形的定义:
有一个角是直角的平行四边形叫做矩形
拓展延伸:
1、已知:矩形ABCD和点P,若PA=PD。
求证:PB=PC。
本题分三种情况思考:
A
A
A
B
B
B
C
C
C
D
D
D
P
P
P
点在形外
点在形上
点在形内
2、如图,把矩形ABCD放置平面直角坐标系中,
已知A(0,0)B(6,0)D(0,4),
求:(1)C点坐标;
(2)若直线y=kx-1将矩形ABCD分成面积相等的两部分,求此直线解析式 。
y
x
A
B
C
D
p
