11.1_全等三角形(2)
文档属性
| 名称 | 11.1_全等三角形(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 440.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-06 00:00:00 | ||
图片预览




文档简介
(共35张PPT)
全等三角形与对应边对应角
◇新人教版◇八年级上册◇
◇新人教版◇八年级上册◇
互相重合的边叫做____
互相重合的角叫做___
其中:互相重合的顶点叫做___
2. 叫做全等三角形。
1.能够重合的两个图形叫做 。
全等形
4.全等三角形的 和 相等
对应边
对应角
对应顶点
能够重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上
全等于
≌
知识梳理:
A
B
C
E
D
F
例如
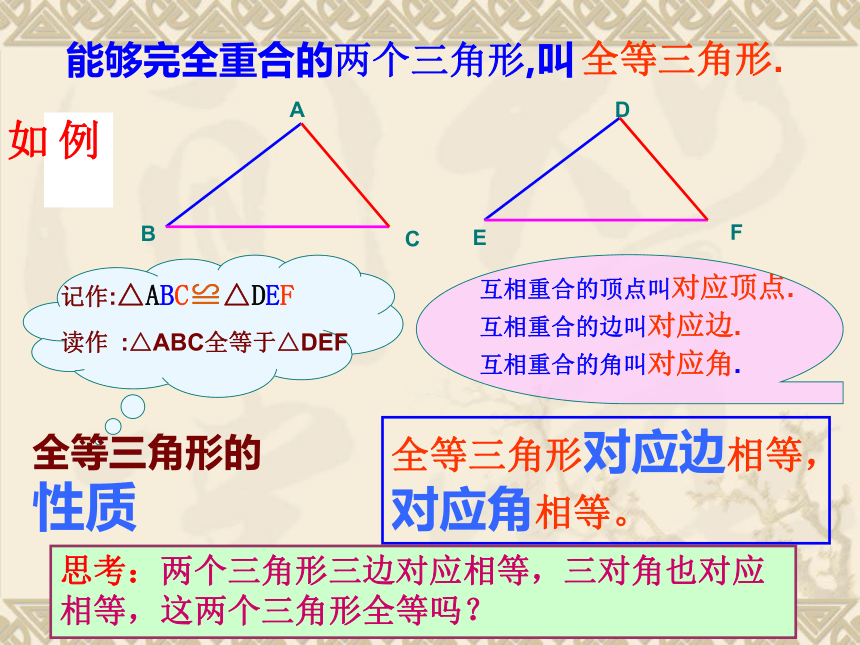
能够完全重合的两个三角形,叫
记作:△ABC≌△DEF
读作 :△ABC全等于△DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
全等三角形.
全等三角形对应边相等,对应角相等。
全等三角形的性质
思考:两个三角形三边对应相等,三对角也对应相等,这两个三角形全等吗?
平移、翻折、旋转
形状、大小都不变
A
B
C
D
E
F
先写出全等式,再指出它们的对应边
和对应角
试一试1:
∵△ABC≌△ADE
∴AB=DE, BC=EF, AC=DF.
∴∠A= ∠D, ∠B= ∠E, ∠C= ∠F.
平移
A
B
C
D
先写出全等式,再指出它们的对应边
和对应角
试一试2:
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,
∠ABC=∠ABD
∠C= ∠D.
规律一:有公共边的,公共边是对应边
翻折
先写出全等式,再指出它们的对应边
和对应角
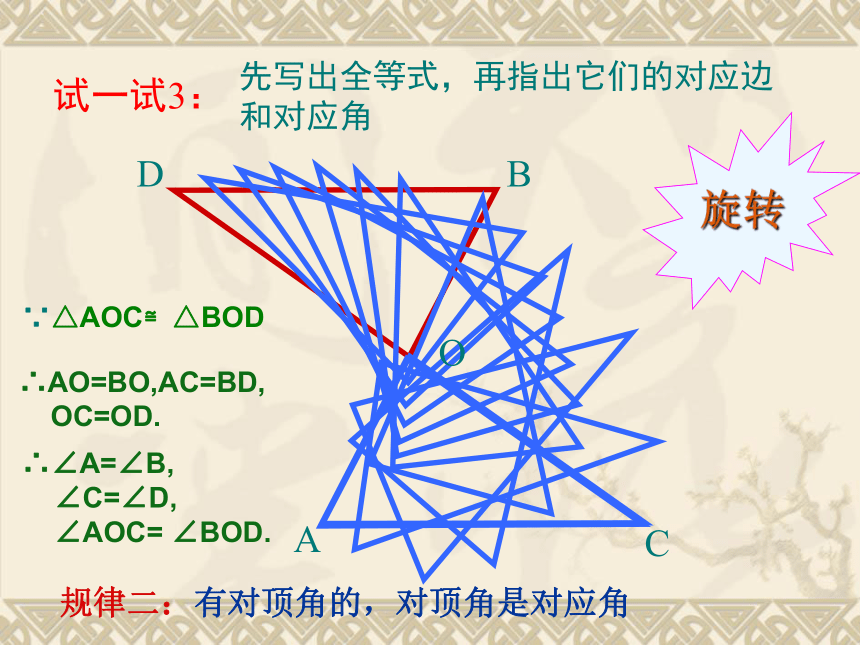
试一试3:
A
C
O
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,
OC=OD.
∴∠A=∠B,
∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
旋转
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
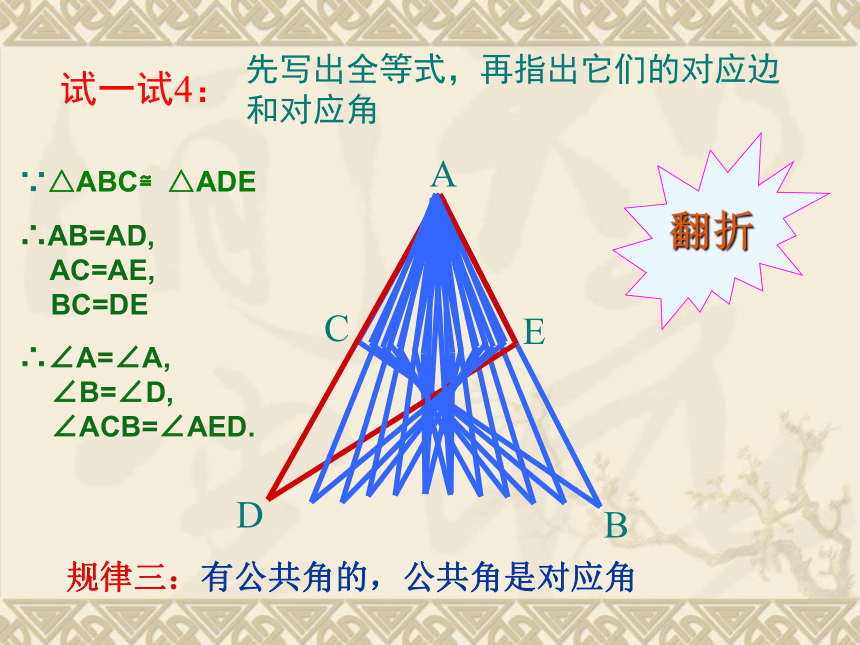
试一试4:
∵△ABC≌△ADE
∴AB=AD,
AC=AE,
BC=DE
∴∠A=∠A,
∠B=∠D,
∠ACB=∠AED.
规律三:有公共角的,公共角是对应角
翻折
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试5:
∵△ABC≌△DEC
∴AB=DE,
AC=DC,
BC=EC
∴∠A=∠D,
∠B=∠E,
∠ACB=∠DCE.
规律四:一对最长的边是对应边
一对最短的边是对应边
旋转
A
D
E
B
C
A
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
先写出全等式,再指出它们的对应边
和对应角
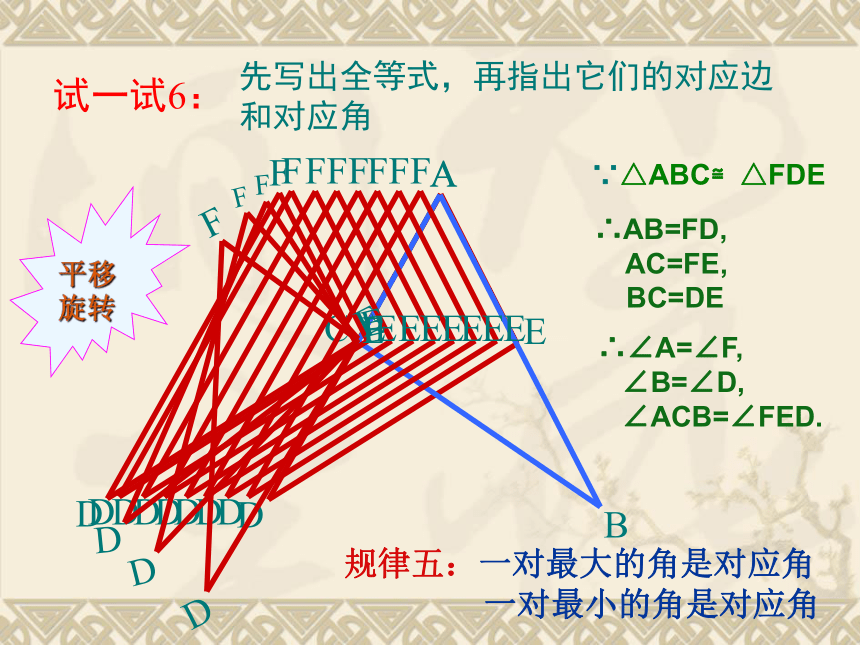
试一试6:
∵△ABC≌△FDE
∴AB=FD,
AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB=∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
平移
旋转
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
对应边所对的角 是对应角,
对应角所对的边 是对应边.
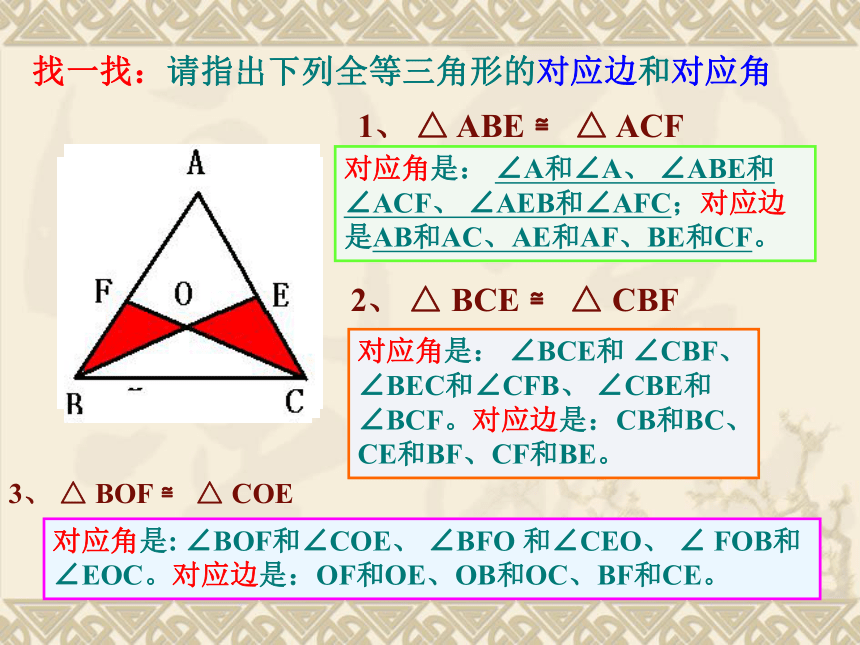
找一找:请指出下列全等三角形的对应边和对应角
1、 △ ABE ≌ △ ACF
对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。
2、 △ BCE ≌ △ CBF
对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。
3、 △ BOF ≌ △ COE
对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。
典型例题
例1 若ΔDEF≌ΔABC, ∠A=70°,∠B=50°,点A的对应点是点D,AB=DE,那么∠F的度数等于( )A.50° B.60° C.50° D.以上都不对
分析: 由∠A=70°,∠B=50°知道:∠C=60°,
所以ΔABC是不等边三角形,
由点A的对应点是点D, AB=DE知道:
∠F的对应角是∠C (=60°)
B
典型例题
例2 如图,若ΔOAD≌ΔOBC, 且∠O=65°,∠C=20°,则∠OAD= .
分析:
由∠O=65°,∠C=20°知道, ∠OBC=95 °,
由ΔOAD≌ΔOBC知: ∠OAD=95 °。
95 °
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:由ΔABC≌ΔAEF和 ∠B=∠E知:AC=AF.所以①是正确的。
①AC=AF,
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:由AB=AE和①AC=AF知: EF=BC ,所以③是正确的。
③EF=BC
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:由③EF=BC知: ∠BAC =∠EAF,
得④ ∠FAC=∠EAB ,
所以④是正确的。
④ ∠FAC=∠EAB
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:因为④∠FAC=∠EAB ,
要使②∠FAB=∠EAB正确,
必须有∠FAC= ∠FAB,
而AF并不是角平分线,
所以②不正确。
C
典型例题
例4:如图,已知ΔABC≌ΔFED, BC=ED, 求证:AB∥EF
证明: ∵ΔABC≌ΔFED,
BC=ED,
∴BC与ED是对应边,
∴∠ =∠ ,
( )
∴ AB∥EF
将上述证明过程补充完整.
A
F
全等三角形的对应角相等
典型例题
例5:如图,已知ΔABD≌ΔAEC, ∠B和∠E是对应角,AB与AE是对应边, 试说明:BC=DE.
分析: 因为ΔABD≌ΔAEC,
并且∠B和∠E是对应角,
所以AD和AC是对应边,
又因为AB与AE是对应边,
所以BD和EC是对应边,
即BD=EC,
所以BD-CD=EC-CD,
所以BC=DE.
练习:
A
B
C
已知:△ ABE≌△ ACD, ∠A=35°,∠B=45°,DC=6cm。
试求:∠ADC的度数,EB的长度
E
D
解: ∵△ ABE ≌△ACD(已知)
∴∠A=∠A ,∠B=∠C,∠AEB=∠ADC
(全等三角形的对应角相等)
EB=DC(全等三角形的对应边相等)
∴EB=6cm
∵ ∠B= 45° ∠A= 35°
∴ ∠AEB=100 °(三角形内角和定例)
∴ ∠ADC=100°
1、全等用符号 表示,读作: 。
2、若△ BCE ≌ △ CBF,则∠CBE= ,
∠BEC= ,BE= , CE= .
3、判断题
1)全等三角形的对应边相等,对应角相等。( )
2)全等三角形的周长相等,面积也相等。 ( )
3)面积相等的三角形是全等三角形。 ( )
4)周长相等的三角形是全等三角形。 ( )
≌
全等于
∠BCF
CF
BF
∠CFB
√
√
X
X
如图:△ABC≌△DBF,找出图中的对应边,对应角.
B
D
A
C
F
答:∠B的对应角是( )
∠C的对应角是( )
∠BAC的对应角是( )
AB的对应边是( )
AC的对应边是( )
BC的对应边是( )
∠B
∠F
∠BDF
DB
DF
BF
A
B
C
D
E
如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△EAB≌ △EDB≌ △EDC,
则∠C的度数是( )0
(A)15 (B)20 (C)25 (D)30
练习3
D
如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,
且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,
求出∠E, ∠ ADE的度数和线段DE,AE 的长度。
B
C
E
D
A
练习4
解: ∵ △ABC≌△AED,(已知)
∴∠E= ∠B= 35°
(全等三角形对应角相等)
∠ADE=∠ACB=18O°- 25°- 35°
=120 ° (全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm
(全等三角形对应边相等)
小结提高
1、回忆这节课,学习了全等三角形的哪些知识?
全等三角形的概念、性质、表示方法、对应写法等
2、找全等三角形对应边、对应角的方法
(1) 大边对应大边,大角对应大角;
(2) 公共边是对应边,公共角是对应角;
(3) 对应边所对的角是对应角,
对应角所对的边是对应边.
1。如图△AOC ≌ △BOD,
求证:AC∥BD
2。如图△ ABD ≌ △CDB,
若AB=4,AD=5,BD=6,
求BC, CD的长。
3。如图△ABD≌ △EBC,
AB=3cm,BC=5cm,
求DE的长
作业:
思考一:
若你手上有一张长方形纸片,你能把它分成两个最大的全等三角形,而总面积又没有变化吗?
思考二:拓展与延伸
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
典型例题
例6:如图,已知ΔAEF是ΔABC绕A点顺时针旋转55°得到的, 求∠BAE,∠CAF和∠BME的度数.
解:因为AE和AF分别是AB和AC旋转后的位置,
所以∠BAE=∠CAF= 55°;
又因为ΔAEF≌ΔABC,
所以∠B=∠E,
因为∠ANB和∠ENM是对顶角,
所以∠BME= ∠BAE= 55°;
∠A+∠B=∠C+∠D
典型例题
例7:如图,已知ΔABE≌ΔACD,且∠1=∠2, ∠B=∠C, 请指出其余的对应边和对应角.
分析:由ΔABE≌ΔACD以及∠1=∠2, ∠B=∠C知:
∠ BAE与∠CAD是对应角,
根据“对应角的对边是对应边 ”
可知:AD与AE,AE与AD,
BE与CD分别是对应边.
如图四边形是长方形,
你能将它分成两个全等的图形吗?
有几种方法?
A
B
C
D
●
O
典型例题
例8:已知ΔABC≌ΔDEF, ΔABC的三边分别为3,m,n, ΔDEF的三边分别为5,p,q,若ΔABC的三边均为整数, 求m+n+p+q的最大值.
解: ∵ΔABC≌ΔDEF
∴根据全等三角形对应边相等,m=5或n=5,
不妨设m=5,在ΔABC中,2<n<8,
∵n为整数, ∴n的最大值等于7,
相应地,p和q应分别取3和7,
∴ m+n+p+q=5+7+3+7=22.
作业:
习题11.1:第1、2 、3 、4题.
全等三角形与对应边对应角
◇新人教版◇八年级上册◇
◇新人教版◇八年级上册◇
互相重合的边叫做____
互相重合的角叫做___
其中:互相重合的顶点叫做___
2. 叫做全等三角形。
1.能够重合的两个图形叫做 。
全等形
4.全等三角形的 和 相等
对应边
对应角
对应顶点
能够重合的两个三角形
3.“全等”用符号“ ”来表示,读作“ ”
对应边
对应角
5.书写全等式时要求把对应字母放在对应
的位置上
全等于
≌
知识梳理:
A
B
C
E
D
F
例如
能够完全重合的两个三角形,叫
记作:△ABC≌△DEF
读作 :△ABC全等于△DEF
互相重合的顶点叫对应顶点.
互相重合的边叫对应边.
互相重合的角叫对应角.
全等三角形.
全等三角形对应边相等,对应角相等。
全等三角形的性质
思考:两个三角形三边对应相等,三对角也对应相等,这两个三角形全等吗?
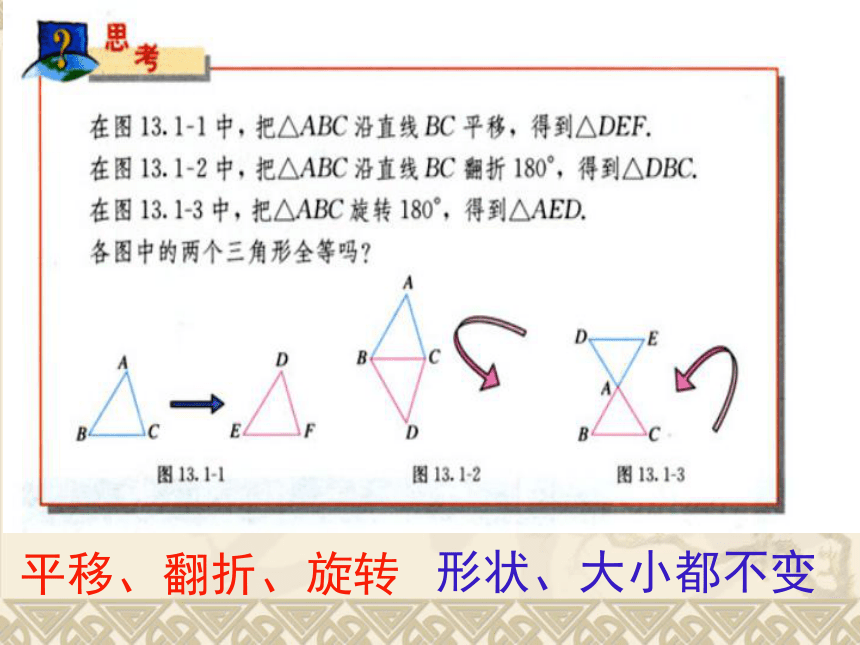
平移、翻折、旋转
形状、大小都不变
A
B
C
D
E
F
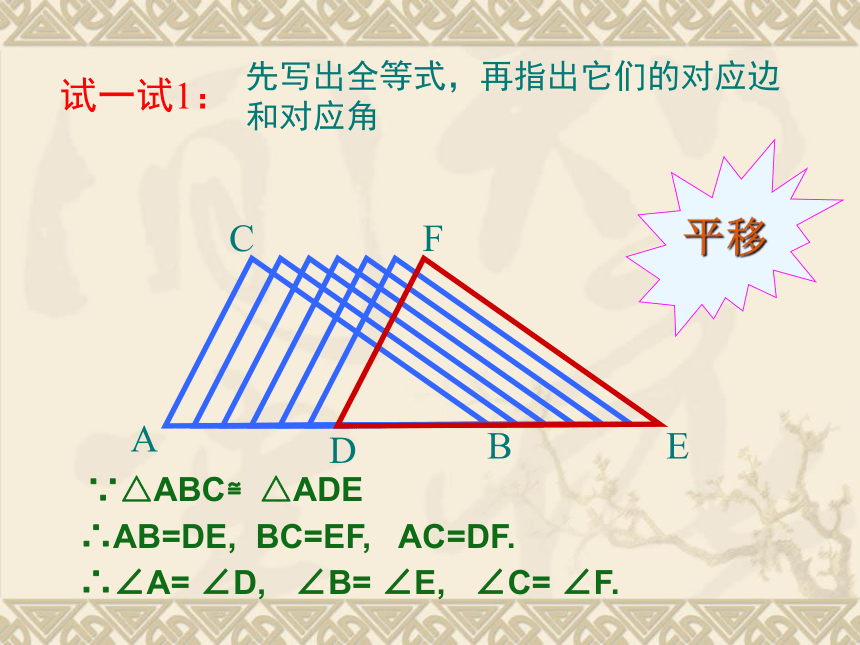
先写出全等式,再指出它们的对应边
和对应角
试一试1:
∵△ABC≌△ADE
∴AB=DE, BC=EF, AC=DF.
∴∠A= ∠D, ∠B= ∠E, ∠C= ∠F.
平移
A
B
C
D
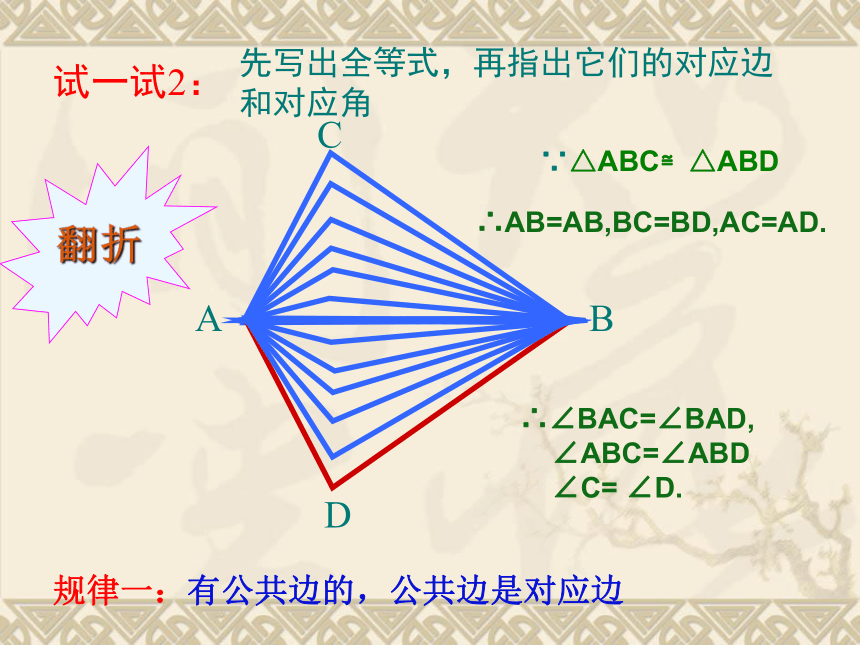
先写出全等式,再指出它们的对应边
和对应角
试一试2:
∵△ABC≌△ABD
∴AB=AB,BC=BD,AC=AD.
∴∠BAC=∠BAD,
∠ABC=∠ABD
∠C= ∠D.
规律一:有公共边的,公共边是对应边
翻折
先写出全等式,再指出它们的对应边
和对应角
试一试3:
A
C
O
D
B
∵△AOC≌△BOD
∴AO=BO,AC=BD,
OC=OD.
∴∠A=∠B,
∠C=∠D,
∠AOC= ∠BOD.
规律二:有对顶角的,对顶角是对应角
旋转
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试4:
∵△ABC≌△ADE
∴AB=AD,
AC=AE,
BC=DE
∴∠A=∠A,
∠B=∠D,
∠ACB=∠AED.
规律三:有公共角的,公共角是对应角
翻折
A
B
C
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试5:
∵△ABC≌△DEC
∴AB=DE,
AC=DC,
BC=EC
∴∠A=∠D,
∠B=∠E,
∠ACB=∠DCE.
规律四:一对最长的边是对应边
一对最短的边是对应边
旋转
A
D
E
B
C
A
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
F
D
E
先写出全等式,再指出它们的对应边
和对应角
试一试6:
∵△ABC≌△FDE
∴AB=FD,
AC=FE,
BC=DE
∴∠A=∠F,
∠B=∠D,
∠ACB=∠FED.
规律五:一对最大的角是对应角
一对最小的角是对应角
平移
旋转
寻找对应元素的规律
(1)有公共边的,公共边是对应边;
(2)有公共角的,公共角是对应角;
(3)有对顶角的,对顶角是对应角;
(4)两个全等三角形最大的边是对应边,
最小的边是对应边;
(5)两个全等三角形最大的角是对应角,
最小的角是对应角;
对应边所对的角 是对应角,
对应角所对的边 是对应边.
找一找:请指出下列全等三角形的对应边和对应角
1、 △ ABE ≌ △ ACF
对应角是: ∠A和∠A、 ∠ABE和∠ACF、 ∠AEB和∠AFC;对应边是AB和AC、AE和AF、BE和CF。
2、 △ BCE ≌ △ CBF
对应角是: ∠BCE和 ∠CBF、 ∠BEC和∠CFB、 ∠CBE和 ∠BCF。对应边是:CB和BC、CE和BF、CF和BE。
3、 △ BOF ≌ △ COE
对应角是: ∠BOF和∠COE、 ∠BFO 和∠CEO、 ∠ FOB和∠EOC。对应边是:OF和OE、OB和OC、BF和CE。
典型例题
例1 若ΔDEF≌ΔABC, ∠A=70°,∠B=50°,点A的对应点是点D,AB=DE,那么∠F的度数等于( )A.50° B.60° C.50° D.以上都不对
分析: 由∠A=70°,∠B=50°知道:∠C=60°,
所以ΔABC是不等边三角形,
由点A的对应点是点D, AB=DE知道:
∠F的对应角是∠C (=60°)
B
典型例题
例2 如图,若ΔOAD≌ΔOBC, 且∠O=65°,∠C=20°,则∠OAD= .
分析:
由∠O=65°,∠C=20°知道, ∠OBC=95 °,
由ΔOAD≌ΔOBC知: ∠OAD=95 °。
95 °
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:由ΔABC≌ΔAEF和 ∠B=∠E知:AC=AF.所以①是正确的。
①AC=AF,
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:由AB=AE和①AC=AF知: EF=BC ,所以③是正确的。
③EF=BC
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:由③EF=BC知: ∠BAC =∠EAF,
得④ ∠FAC=∠EAB ,
所以④是正确的。
④ ∠FAC=∠EAB
典型例题
例3:如图,若ΔABC≌ΔAEF, AB=AE,∠B=∠E,则下列结论:①AC=AF, ②∠FAB=∠EAB, ③EF=BC,④ ∠FAC=∠EAB,其中正确结论的个数是( ) A.1个 B.2个 C.3个 D.4个
分析:因为④∠FAC=∠EAB ,
要使②∠FAB=∠EAB正确,
必须有∠FAC= ∠FAB,
而AF并不是角平分线,
所以②不正确。
C
典型例题
例4:如图,已知ΔABC≌ΔFED, BC=ED, 求证:AB∥EF
证明: ∵ΔABC≌ΔFED,
BC=ED,
∴BC与ED是对应边,
∴∠ =∠ ,
( )
∴ AB∥EF
将上述证明过程补充完整.
A
F
全等三角形的对应角相等
典型例题
例5:如图,已知ΔABD≌ΔAEC, ∠B和∠E是对应角,AB与AE是对应边, 试说明:BC=DE.
分析: 因为ΔABD≌ΔAEC,
并且∠B和∠E是对应角,
所以AD和AC是对应边,
又因为AB与AE是对应边,
所以BD和EC是对应边,
即BD=EC,
所以BD-CD=EC-CD,
所以BC=DE.
练习:
A
B
C
已知:△ ABE≌△ ACD, ∠A=35°,∠B=45°,DC=6cm。
试求:∠ADC的度数,EB的长度
E
D
解: ∵△ ABE ≌△ACD(已知)
∴∠A=∠A ,∠B=∠C,∠AEB=∠ADC
(全等三角形的对应角相等)
EB=DC(全等三角形的对应边相等)
∴EB=6cm
∵ ∠B= 45° ∠A= 35°
∴ ∠AEB=100 °(三角形内角和定例)
∴ ∠ADC=100°
1、全等用符号 表示,读作: 。
2、若△ BCE ≌ △ CBF,则∠CBE= ,
∠BEC= ,BE= , CE= .
3、判断题
1)全等三角形的对应边相等,对应角相等。( )
2)全等三角形的周长相等,面积也相等。 ( )
3)面积相等的三角形是全等三角形。 ( )
4)周长相等的三角形是全等三角形。 ( )
≌
全等于
∠BCF
CF
BF
∠CFB
√
√
X
X
如图:△ABC≌△DBF,找出图中的对应边,对应角.
B
D
A
C
F
答:∠B的对应角是( )
∠C的对应角是( )
∠BAC的对应角是( )
AB的对应边是( )
AC的对应边是( )
BC的对应边是( )
∠B
∠F
∠BDF
DB
DF
BF
A
B
C
D
E
如图所示,在△ABC中,D、E分别是边AC、BC上的点,若△EAB≌ △EDB≌ △EDC,
则∠C的度数是( )0
(A)15 (B)20 (C)25 (D)30
练习3
D
如图,△ABC≌△AED,AB是△ABC的最大边,AE是△AED的最大边, ∠BAC 与∠ EAD对应角,
且∠BAC=25°, ∠B=35°,AB=3cm,BC=1cm,
求出∠E, ∠ ADE的度数和线段DE,AE 的长度。
B
C
E
D
A
练习4
解: ∵ △ABC≌△AED,(已知)
∴∠E= ∠B= 35°
(全等三角形对应角相等)
∠ADE=∠ACB=18O°- 25°- 35°
=120 ° (全等三角形对应角相等)
DE=BC=1cm, AE=AB=3cm
(全等三角形对应边相等)
小结提高
1、回忆这节课,学习了全等三角形的哪些知识?
全等三角形的概念、性质、表示方法、对应写法等
2、找全等三角形对应边、对应角的方法
(1) 大边对应大边,大角对应大角;
(2) 公共边是对应边,公共角是对应角;
(3) 对应边所对的角是对应角,
对应角所对的边是对应边.
1。如图△AOC ≌ △BOD,
求证:AC∥BD
2。如图△ ABD ≌ △CDB,
若AB=4,AD=5,BD=6,
求BC, CD的长。
3。如图△ABD≌ △EBC,
AB=3cm,BC=5cm,
求DE的长
作业:
思考一:
若你手上有一张长方形纸片,你能把它分成两个最大的全等三角形,而总面积又没有变化吗?
思考二:拓展与延伸
下图是一个等边三角形,你能把它分成两个全等三角形吗?你能把它分成三个全等三角形吗?四个呢?
典型例题
例6:如图,已知ΔAEF是ΔABC绕A点顺时针旋转55°得到的, 求∠BAE,∠CAF和∠BME的度数.
解:因为AE和AF分别是AB和AC旋转后的位置,
所以∠BAE=∠CAF= 55°;
又因为ΔAEF≌ΔABC,
所以∠B=∠E,
因为∠ANB和∠ENM是对顶角,
所以∠BME= ∠BAE= 55°;
∠A+∠B=∠C+∠D
典型例题
例7:如图,已知ΔABE≌ΔACD,且∠1=∠2, ∠B=∠C, 请指出其余的对应边和对应角.
分析:由ΔABE≌ΔACD以及∠1=∠2, ∠B=∠C知:
∠ BAE与∠CAD是对应角,
根据“对应角的对边是对应边 ”
可知:AD与AE,AE与AD,
BE与CD分别是对应边.
如图四边形是长方形,
你能将它分成两个全等的图形吗?
有几种方法?
A
B
C
D
●
O
典型例题
例8:已知ΔABC≌ΔDEF, ΔABC的三边分别为3,m,n, ΔDEF的三边分别为5,p,q,若ΔABC的三边均为整数, 求m+n+p+q的最大值.
解: ∵ΔABC≌ΔDEF
∴根据全等三角形对应边相等,m=5或n=5,
不妨设m=5,在ΔABC中,2<n<8,
∵n为整数, ∴n的最大值等于7,
相应地,p和q应分别取3和7,
∴ m+n+p+q=5+7+3+7=22.
作业:
习题11.1:第1、2 、3 、4题.
