1.3.1 推出充分条件、必要条件 (PPT)—2021-2022学年高二上学期数学人教B版选修1-1(16张PPT)
文档属性
| 名称 | 1.3.1 推出充分条件、必要条件 (PPT)—2021-2022学年高二上学期数学人教B版选修1-1(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 405.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览






文档简介
1.3.1 推出与充分条件、必要条件
二、引入课题
党的十八大以来,国家将生态文明建设作为中华民族可持续发展的根本大计 。习近平总书记也提出了“绿水青山就是金山银山”的科学论断。
情境引入:水是生命之源,万物之本。
思考:“水”和“人类生存”之间存在着一定的逻辑关系,那么从数学的角度如何去定义呢?
三、复习旧知,引入概念
问题2:指出下列“若p,则q”形式的命题的条件和结论,并判断其真假。
(1)若x=5,则 =25.
(2)若小明是中国人,则他一定是宁夏人。
结论:如果“若p,则q”形式的命题是一个真命题,那么我们就说p可以推出q,符号表示为“p?q”
“若p,则q”形式的命题是一个假命题,那么我们就说p不可以推出q,符号表示为“p q ”。
问题1:你能举出数学和生活当中“若p,则q”形式的命题的例子吗?
四、建构概念
充分条件和必要条件的概念:“若p,则q”形式的命题是真命题,即p?q,则称p是q的充分条件,q是p的必要条件。
问题3:请同学们把下列命题补充完整,使它成为一个真命题。
若x=_____,则 =1?
五、剖析定义,揭示本质
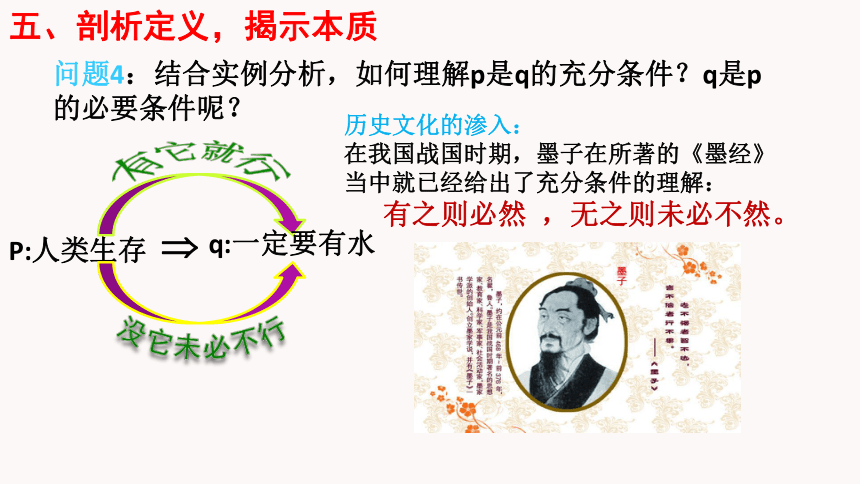
问题4:结合实例分析,如何理解p是q的充分条件?q是p的必要条件呢?
P:人类生存
有它就行
历史文化的渗入:
在我国战国时期,墨子在所著的《墨经》
当中就已经给出了充分条件的理解:
有之则必然 ,无之则未必不然。
没它未必不行
?
q:一定要有水
六、类比研究,深化理解
P:人类生存?q:一定要有水
有它未必行
没它一定不行
墨子在《墨经》当中不仅给出了充分条件的理解,还给出了必要条件的理解:
无之则必不然,有之则未必然。
七、内化新知、抽象归纳
结论:其实质是判断命题“若p,则q”是真命题还是假命题,或者判断p能否推出q.
问题5:如何判断p是q的充分条件,q是p的必要条件呢?
同一种逻辑关系的四种不同的表达形式
文字表达
符号表达
逻辑表达1
逻辑表达2
“若p,则q”为真 p?q; p是q的充分条件; q是p的必要条件
八、巩固练习,知识反馈
例1:在下列各组命题中,p是q的充分条件吗?
(1)p:两三角形全等,q: 两三角形面积相等.
解:∵p ?q, ∴p是q的充分条件
(2)p: =4,q: a=2.
解: ∵p q, ∴p不是q的充分条件
例2:在下面各组命题中,q是p的必要条件吗?
(1)p:x=0, q: xy=0.
解:∵p ?q, ∴q是p的必要条件
(2)p: 鸟会飞, q: 鸟有翅膀.
解:∵p ?q, ∴q是p的必要条件
(3)p:水,q:人类生存.
解: ∵p q, ∴q不是p的必要条件
C
问题6:p:开关C闭合,q:灯泡亮.p是q的什么条件?
九、充要条件
结论:开关闭合,灯泡一定亮,即p?q,
灯泡亮,开关一定闭合,即q ?p,
充要条件的概念:若p?q,且q ?p,则p是q的充要条件
十、归纳完善
P是q的充分条件( p?q )
p是q的充分不必要条件(p?q但q p)
P是q的充要条件
(p?q且q ?p)
p是q的必要条件
(q ?p )
P是q的必要不充分条件
(p q但q ?p)
P是q的充要条件
(p?q且q ?p)
p 是q的即不充分也不必要条件
P q且q p
①
②
③
④
一般判断p是q的什么条件时,需从两方面考虑,一是p能否推出q,二是q能否推出p。
十一、问题创造,合作探究
活动一(自主命题):
分组讨论,请同学们编制“若p则q”形式的命题,
并判断p是q的什么条件。
活动二(自主探究):
p:若我生活在宁夏,q:则我一定生活
在中国,则p是q的___________条件?
思考:当p是q的充分不必要条件时,集合A和集合B具有怎样的包含关系?
P:集合A
P:集合B
中国(B)
宁夏(A)
十二、类比联想、知识迁移
问题7:已知p:xA,q:x B,根据已给的条件同学们共同完成下表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}条件关系
符号表示
集合表示
维恩图
P是q的充分条件
P是q的必要条件
P是q的充分不必要条件
P时q的必要不充分条件
P是q的既不充分又不必要条件
P是q的充要条件
但
但
B
A
A
B
B?A
A B
B A
A
A(B)
B
A
B
B
A
B
A ?B,B ?A
且
A=B
十三、创造问题,数学建模
例4.P:x>a,q:x>1.
(2)当a>0时,p是q的什么条件?
(判断P是q的充分条件还是必要条件?)
(1)当a=3时,p是q的什么条件?
解:当0 q ?p
∴p是q的必要条件
当a≥ 1时, p?q
∴p是q的充分条件
x
0
1
。
q
。
a
0
1
。
a
q
p
p
。
x
十四、回顾反思、梳理总结
思考:回顾知识的形成过程,相互交流,谈谈你对本节课的认识!
十五、巩固所学、课堂延伸
1.(1)教材21页,练习A组2,3
(2)教材22页,练习B组1,2
一、课后作业:
1.思考:“若p,则q”,是一个真命题,能否从充分条件与必要条件的定义角度,解释说明“若﹁q,则﹁p”也是一个真命题?
二、课外作业
2.在网上查阅有关墨子的相关资料,进一步深刻理解:
有之则必然,无之则未必不然。
有之则未必然,无之则必不然。
二、引入课题
党的十八大以来,国家将生态文明建设作为中华民族可持续发展的根本大计 。习近平总书记也提出了“绿水青山就是金山银山”的科学论断。
情境引入:水是生命之源,万物之本。
思考:“水”和“人类生存”之间存在着一定的逻辑关系,那么从数学的角度如何去定义呢?
三、复习旧知,引入概念
问题2:指出下列“若p,则q”形式的命题的条件和结论,并判断其真假。
(1)若x=5,则 =25.
(2)若小明是中国人,则他一定是宁夏人。
结论:如果“若p,则q”形式的命题是一个真命题,那么我们就说p可以推出q,符号表示为“p?q”
“若p,则q”形式的命题是一个假命题,那么我们就说p不可以推出q,符号表示为“p q ”。
问题1:你能举出数学和生活当中“若p,则q”形式的命题的例子吗?
四、建构概念
充分条件和必要条件的概念:“若p,则q”形式的命题是真命题,即p?q,则称p是q的充分条件,q是p的必要条件。
问题3:请同学们把下列命题补充完整,使它成为一个真命题。
若x=_____,则 =1?
五、剖析定义,揭示本质
问题4:结合实例分析,如何理解p是q的充分条件?q是p的必要条件呢?
P:人类生存
有它就行
历史文化的渗入:
在我国战国时期,墨子在所著的《墨经》
当中就已经给出了充分条件的理解:
有之则必然 ,无之则未必不然。
没它未必不行
?
q:一定要有水
六、类比研究,深化理解
P:人类生存?q:一定要有水
有它未必行
没它一定不行
墨子在《墨经》当中不仅给出了充分条件的理解,还给出了必要条件的理解:
无之则必不然,有之则未必然。
七、内化新知、抽象归纳
结论:其实质是判断命题“若p,则q”是真命题还是假命题,或者判断p能否推出q.
问题5:如何判断p是q的充分条件,q是p的必要条件呢?
同一种逻辑关系的四种不同的表达形式
文字表达
符号表达
逻辑表达1
逻辑表达2
“若p,则q”为真 p?q; p是q的充分条件; q是p的必要条件
八、巩固练习,知识反馈
例1:在下列各组命题中,p是q的充分条件吗?
(1)p:两三角形全等,q: 两三角形面积相等.
解:∵p ?q, ∴p是q的充分条件
(2)p: =4,q: a=2.
解: ∵p q, ∴p不是q的充分条件
例2:在下面各组命题中,q是p的必要条件吗?
(1)p:x=0, q: xy=0.
解:∵p ?q, ∴q是p的必要条件
(2)p: 鸟会飞, q: 鸟有翅膀.
解:∵p ?q, ∴q是p的必要条件
(3)p:水,q:人类生存.
解: ∵p q, ∴q不是p的必要条件
C
问题6:p:开关C闭合,q:灯泡亮.p是q的什么条件?
九、充要条件
结论:开关闭合,灯泡一定亮,即p?q,
灯泡亮,开关一定闭合,即q ?p,
充要条件的概念:若p?q,且q ?p,则p是q的充要条件
十、归纳完善
P是q的充分条件( p?q )
p是q的充分不必要条件(p?q但q p)
P是q的充要条件
(p?q且q ?p)
p是q的必要条件
(q ?p )
P是q的必要不充分条件
(p q但q ?p)
P是q的充要条件
(p?q且q ?p)
p 是q的即不充分也不必要条件
P q且q p
①
②
③
④
一般判断p是q的什么条件时,需从两方面考虑,一是p能否推出q,二是q能否推出p。
十一、问题创造,合作探究
活动一(自主命题):
分组讨论,请同学们编制“若p则q”形式的命题,
并判断p是q的什么条件。
活动二(自主探究):
p:若我生活在宁夏,q:则我一定生活
在中国,则p是q的___________条件?
思考:当p是q的充分不必要条件时,集合A和集合B具有怎样的包含关系?
P:集合A
P:集合B
中国(B)
宁夏(A)
十二、类比联想、知识迁移
问题7:已知p:xA,q:x B,根据已给的条件同学们共同完成下表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}条件关系
符号表示
集合表示
维恩图
P是q的充分条件
P是q的必要条件
P是q的充分不必要条件
P时q的必要不充分条件
P是q的既不充分又不必要条件
P是q的充要条件
但
但
B
A
A
B
B?A
A B
B A
A
A(B)
B
A
B
B
A
B
A ?B,B ?A
且
A=B
十三、创造问题,数学建模
例4.P:x>a,q:x>1.
(2)当a>0时,p是q的什么条件?
(判断P是q的充分条件还是必要条件?)
(1)当a=3时,p是q的什么条件?
解:当0 q ?p
∴p是q的必要条件
当a≥ 1时, p?q
∴p是q的充分条件
x
0
1
。
q
。
a
0
1
。
a
q
p
p
。
x
十四、回顾反思、梳理总结
思考:回顾知识的形成过程,相互交流,谈谈你对本节课的认识!
十五、巩固所学、课堂延伸
1.(1)教材21页,练习A组2,3
(2)教材22页,练习B组1,2
一、课后作业:
1.思考:“若p,则q”,是一个真命题,能否从充分条件与必要条件的定义角度,解释说明“若﹁q,则﹁p”也是一个真命题?
二、课外作业
2.在网上查阅有关墨子的相关资料,进一步深刻理解:
有之则必然,无之则未必不然。
有之则未必然,无之则必不然。
