1.3.2 命题的四种形式 (共16张PPT)—2021-2022学年高二上学期数学人教B版选修1-1
文档属性
| 名称 | 1.3.2 命题的四种形式 (共16张PPT)—2021-2022学年高二上学期数学人教B版选修1-1 |

|
|
| 格式 | ppt | ||
| 文件大小 | 524.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
1.3.2
命题的四种形式
这是老师在期中考试前听到的一位家长和一个孩子的对话。
家长:“你能考进班里前五名,我就给你买手机。”
孩子回答到:“你给我买手机,我就能考进班里的前五名。”
家长:“你不能考进班里的前五名,我就不给你买手机。”
孩子想了想说:“你不给我买手机,我就不能考进班里的前五名。”
引例:
(1)同位角相等,两直线平行;
(2)两直线平行,同位角相等;
(3)同位角不相等,两直线不平行;
(4)两直线不平行,同位角不相等。
上述四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?
(1)原命题:如果p,则q.
(2)条件和结论“换位”得
如果q,则p,这称为原命题的逆命题;
(3)条件和结论“换质”(分别否定)得
如果非p,则非q,这称为原命题的否命题;
(4)条件和结论“换位”又“换质”得
如果非q,则非p,这称为原命题的逆否命题;
一、命题的四种形式
若p为原命题条件,q为原命题结论,则:
原命题:
若
p
,则
q
逆命题:
若
q,则
p
否命题:
若
?p,
则
?q
逆否命题:若
?q
,则
?p
原命题
若p,则q
逆否命题
若?
q,则?
p
否命题
若?
p,则?
q
逆命题
若q,则p
互逆
互
否
互
否
互逆
互为逆否
同真同假
命题的四种形式中谁是原命题是相对的,而不是绝对的.
如设图中④是原命题,则它的逆命题、否命题、逆否命题依次是③、②、①.
p?q??q??p
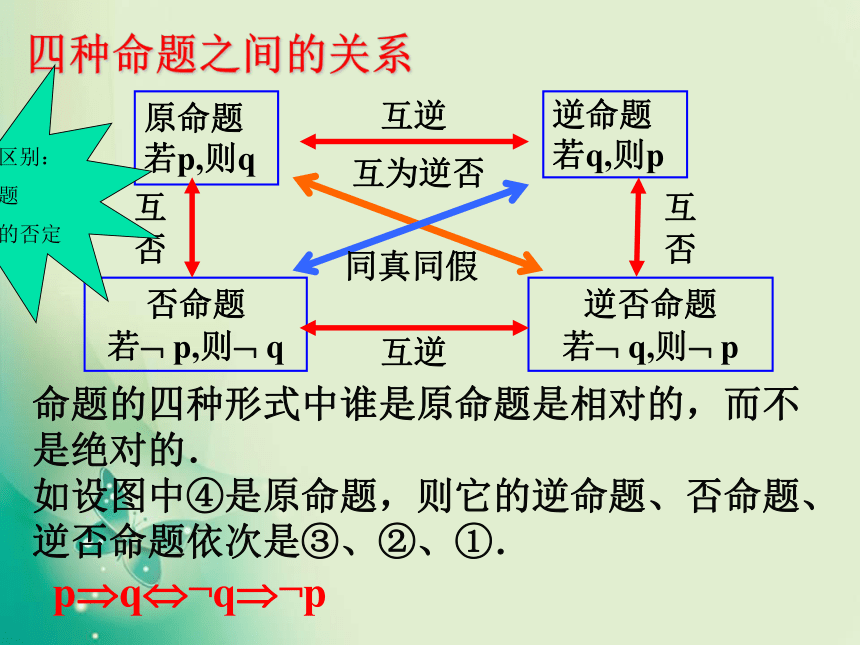
四种命题之间的关系
注意区别:
否命题
命题的否定
2)原命题:若a=0,
则ab=0。
逆命题:若ab=0,
则a=0。
否命题:若a≠
0,
则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
(真)
四种命题的真假性是否有一定的相互关系呢?
例子:
1)原命题:若x=2或x=3,
则x2-5x+6=0。
逆命题:若x2-5x+6=0,
则x=2或x=3。
否命题:若x≠2且x≠3,
则x2-5x+6≠0
。
逆否命题:若x2-5x+6≠0,则x≠2且x≠3。
(真)
(真)
(真)
3)
原命题:若a
>
b,
则
ac2>bc2。
逆命题:若ac2>bc2,则a>b。
否命题:若a≤b,则ac2≤bc2。
逆否命题:若ac2≤bc2,则a≤b。
(假)
(真)
(真)
(假)
想一想:
由以上三例我们能发现四种命题真假性有什么关系?
原命题
逆命题
否命题
逆否命题
一般地,四种命题的真假性,有而且仅有下面四种情况:
四种命题的真假性间有什么规律呢?
真
真
真
真
真
假
假
假
假
假
假
假
假
真
真
真
(1)两个命题互为逆否命题,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系。
结
论:
原命题与逆否命题同真假。
原命题的逆命题与否命题同真假。
(2)两个命题为互逆命题或互否命题,它们的真假性
没有关系。
(1)
p?q??q??p
例2.设原命题是“当c>0时,若a>b,则ac>bc”,写出它的逆命题、否命题与逆否命题,并分别判断它们的真假.
解:
逆命题:当c
>0
时,若ac
>bc
,则a
>b.
逆命题为真.
否命题:当c
>0
时,若a
≤b
,则ac
≤
bc
.
否命题为真.
逆否命题:当c
>0
时,若ac
≤
bc
,则a
≤b
.
逆否命题为真.
1.命题“内错角相等,则两直线平行”的否命题为(
)
A.两直线平行,内错角相等
B.两直线不平行,则内错角不相等
C.内错角不相等,则两直线不平行
D.内错角不相等,则两直线平行
2.写出“若x2+y2=0,则x=0且y=0”的逆否命题:
;
练习:
3.把下列命题写成“若p则q”的形式,并判断其真假.
(1)实数的平方是非负数;
(2)等底等高的两个三角形是全等三角形;
(3)能被6整除的数既能被3整除也能被2整除;
(4)弦的垂直平分线经过圆心,并平分弦所对的弧.
4.写出命题“若a和b都是偶数,则a+b是偶数”的否命题和逆否命题.
5.判断命题“若x+y≤5,则x≤2或y≤3”的真假.
7.
下列四个命题中真命题是
①“若xy=1,则x、y互为倒数”的逆命题
②“面积相等的三角形全等”的否命题
③“若m≤1,则方程x2-2x+m=0有实根”的逆否命题
④“若A∩B=B,则A
B”的逆否命题
A.①②
B.②③
C.①②③
D.③④
课堂小结:
原命题:
逆命题:
否命题:
逆否命题:
若p则q.
若q则p.
若?p则?q.
若?q则?p.
1、四种命题形式:
2、四种命题间的相互关系及其真假性的关系
通过这节课的学习,你学到了那些知识呢?
1.3.2
命题的四种形式
这是老师在期中考试前听到的一位家长和一个孩子的对话。
家长:“你能考进班里前五名,我就给你买手机。”
孩子回答到:“你给我买手机,我就能考进班里的前五名。”
家长:“你不能考进班里的前五名,我就不给你买手机。”
孩子想了想说:“你不给我买手机,我就不能考进班里的前五名。”
引例:
(1)同位角相等,两直线平行;
(2)两直线平行,同位角相等;
(3)同位角不相等,两直线不平行;
(4)两直线不平行,同位角不相等。
上述四个命题中,命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系?
(1)原命题:如果p,则q.
(2)条件和结论“换位”得
如果q,则p,这称为原命题的逆命题;
(3)条件和结论“换质”(分别否定)得
如果非p,则非q,这称为原命题的否命题;
(4)条件和结论“换位”又“换质”得
如果非q,则非p,这称为原命题的逆否命题;
一、命题的四种形式
若p为原命题条件,q为原命题结论,则:
原命题:
若
p
,则
q
逆命题:
若
q,则
p
否命题:
若
?p,
则
?q
逆否命题:若
?q
,则
?p
原命题
若p,则q
逆否命题
若?
q,则?
p
否命题
若?
p,则?
q
逆命题
若q,则p
互逆
互
否
互
否
互逆
互为逆否
同真同假
命题的四种形式中谁是原命题是相对的,而不是绝对的.
如设图中④是原命题,则它的逆命题、否命题、逆否命题依次是③、②、①.
p?q??q??p
四种命题之间的关系
注意区别:
否命题
命题的否定
2)原命题:若a=0,
则ab=0。
逆命题:若ab=0,
则a=0。
否命题:若a≠
0,
则ab≠0。
逆否命题:若ab≠0,则a≠0。
(真)
(假)
(假)
(真)
(真)
四种命题的真假性是否有一定的相互关系呢?
例子:
1)原命题:若x=2或x=3,
则x2-5x+6=0。
逆命题:若x2-5x+6=0,
则x=2或x=3。
否命题:若x≠2且x≠3,
则x2-5x+6≠0
。
逆否命题:若x2-5x+6≠0,则x≠2且x≠3。
(真)
(真)
(真)
3)
原命题:若a
>
b,
则
ac2>bc2。
逆命题:若ac2>bc2,则a>b。
否命题:若a≤b,则ac2≤bc2。
逆否命题:若ac2≤bc2,则a≤b。
(假)
(真)
(真)
(假)
想一想:
由以上三例我们能发现四种命题真假性有什么关系?
原命题
逆命题
否命题
逆否命题
一般地,四种命题的真假性,有而且仅有下面四种情况:
四种命题的真假性间有什么规律呢?
真
真
真
真
真
假
假
假
假
假
假
假
假
真
真
真
(1)两个命题互为逆否命题,它们有相同的真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性没有关系。
结
论:
原命题与逆否命题同真假。
原命题的逆命题与否命题同真假。
(2)两个命题为互逆命题或互否命题,它们的真假性
没有关系。
(1)
p?q??q??p
例2.设原命题是“当c>0时,若a>b,则ac>bc”,写出它的逆命题、否命题与逆否命题,并分别判断它们的真假.
解:
逆命题:当c
>0
时,若ac
>bc
,则a
>b.
逆命题为真.
否命题:当c
>0
时,若a
≤b
,则ac
≤
bc
.
否命题为真.
逆否命题:当c
>0
时,若ac
≤
bc
,则a
≤b
.
逆否命题为真.
1.命题“内错角相等,则两直线平行”的否命题为(
)
A.两直线平行,内错角相等
B.两直线不平行,则内错角不相等
C.内错角不相等,则两直线不平行
D.内错角不相等,则两直线平行
2.写出“若x2+y2=0,则x=0且y=0”的逆否命题:
;
练习:
3.把下列命题写成“若p则q”的形式,并判断其真假.
(1)实数的平方是非负数;
(2)等底等高的两个三角形是全等三角形;
(3)能被6整除的数既能被3整除也能被2整除;
(4)弦的垂直平分线经过圆心,并平分弦所对的弧.
4.写出命题“若a和b都是偶数,则a+b是偶数”的否命题和逆否命题.
5.判断命题“若x+y≤5,则x≤2或y≤3”的真假.
7.
下列四个命题中真命题是
①“若xy=1,则x、y互为倒数”的逆命题
②“面积相等的三角形全等”的否命题
③“若m≤1,则方程x2-2x+m=0有实根”的逆否命题
④“若A∩B=B,则A
B”的逆否命题
A.①②
B.②③
C.①②③
D.③④
课堂小结:
原命题:
逆命题:
否命题:
逆否命题:
若p则q.
若q则p.
若?p则?q.
若?q则?p.
1、四种命题形式:
2、四种命题间的相互关系及其真假性的关系
通过这节课的学习,你学到了那些知识呢?
