_2.3.2平面向量基本定理 课件(共25张PPT)2020-2021学年高中数学北师大版必修4
文档属性
| 名称 | _2.3.2平面向量基本定理 课件(共25张PPT)2020-2021学年高中数学北师大版必修4 |

|
|
| 格式 | ppt | ||
| 文件大小 | 622.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-08 21:30:18 | ||
图片预览




文档简介
(共25张PPT)
2.3.2
平面向量基本定理
北师大版
复习回顾
1.
向量加法与减法有哪几种几何运算法则?
2.怎样理解向量的数乘运算
?
λ>0时,
与
方向________
;
λ<0时,
与
方向________
;
λ=0时,
=________
__________
相反
相同
3.平面向量共线定理是什么?
非零向量a与向量b共线
存在唯一实数λ,使b=λa.
知识点 平面向量基本定理
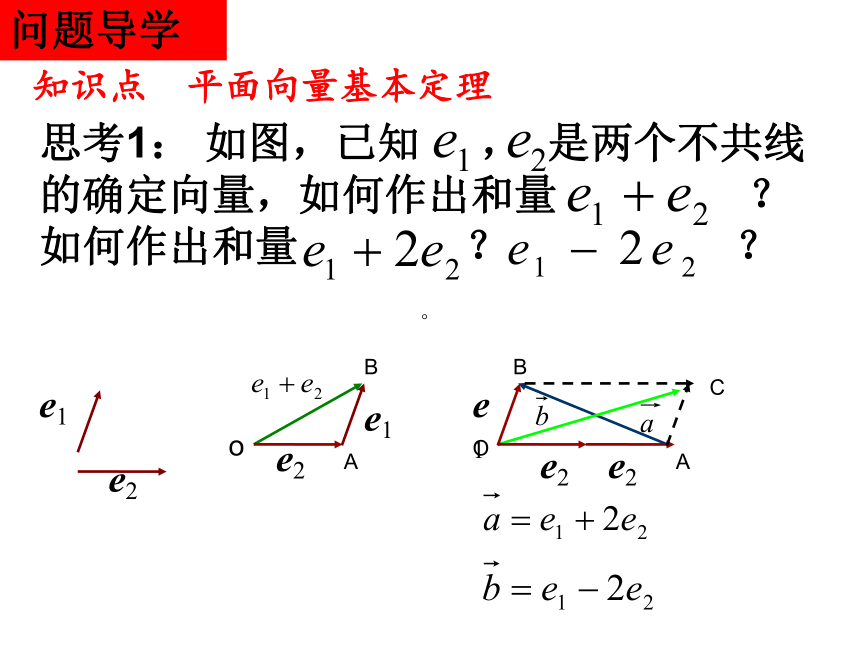
思考1:
如图,已知
,
是两个不共线的确定向量,如何作出和量
?如何作出和量
?
?
e1
e2
e2
o
A
e1
B
e2
O
e2
A
e1
B
C
问题导学
°
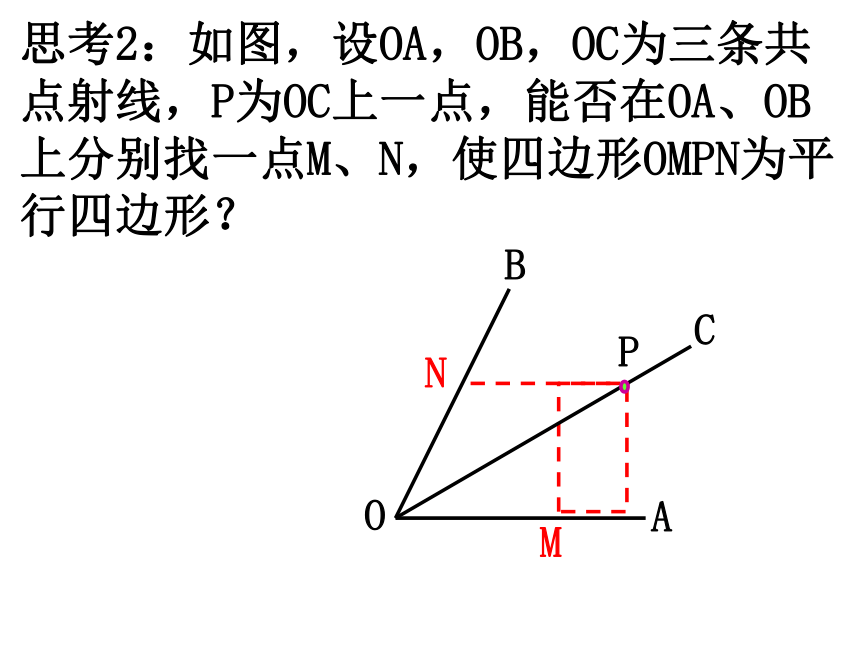
思考2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?
M
N
O
A
B
C
P
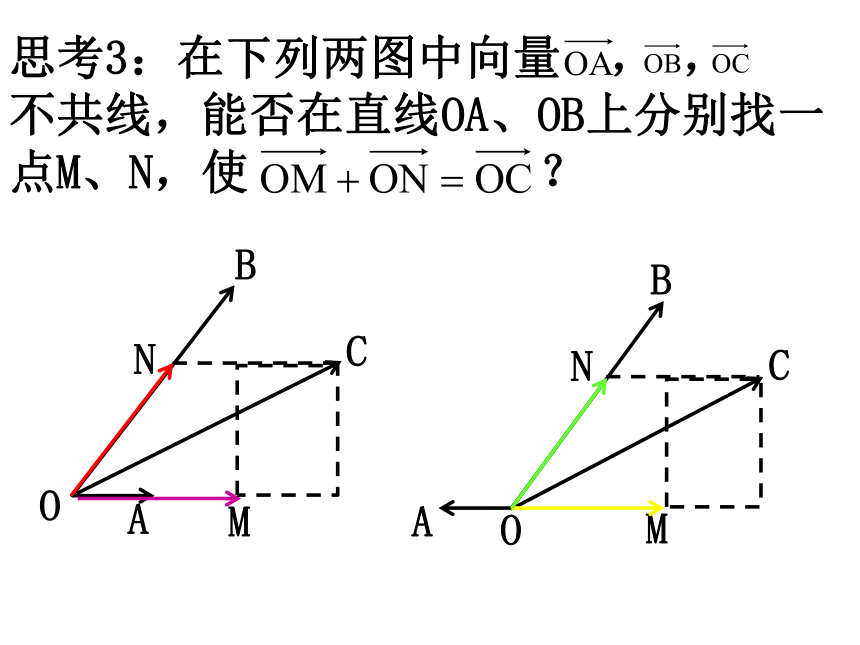
思考3:在下列两图中向量
,
,
不共线,能否在直线OA、OB上分别找一点M、N,使
?
O
A
B
C
M
N
O
A
B
C
M
N
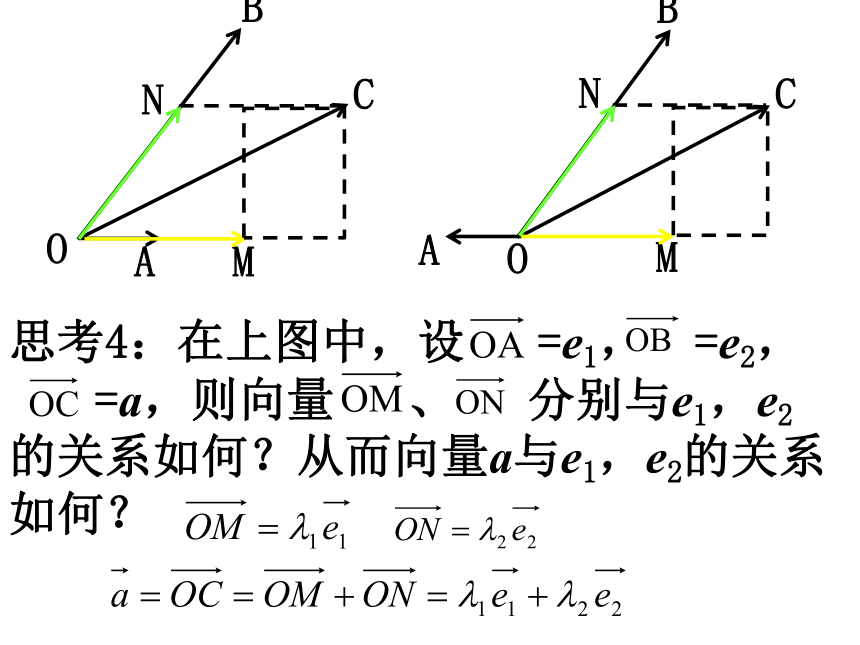
思考4:在上图中,设
=e1,
=e2,
=a,则向量
、
分别与e1,e2的关系如何?从而向量a与e1,e2的关系如何?
O
A
B
C
M
N
O
A
B
C
M
N
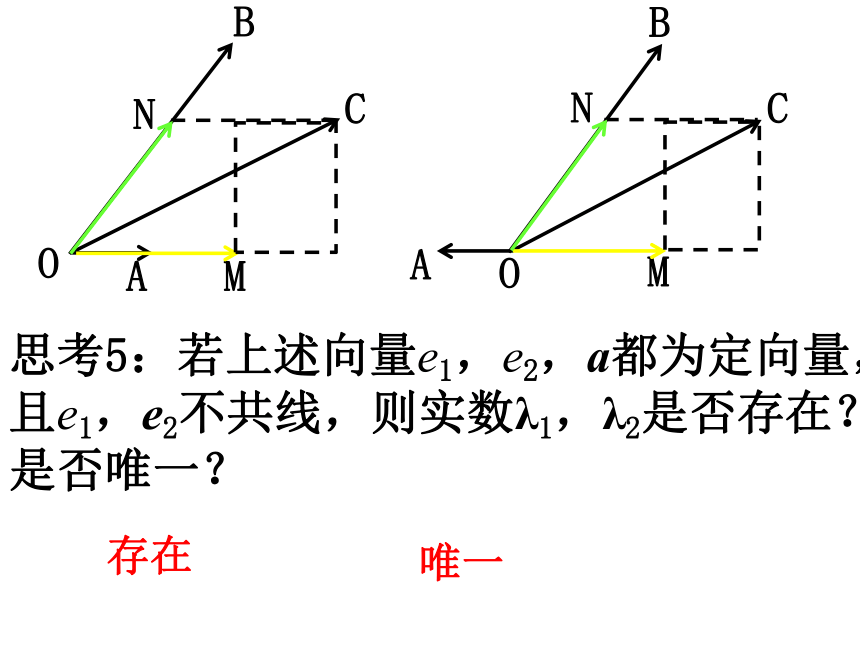
思考5:若上述向量e1,e2,a都为定向量,且e1,e2不共线,则实数λ1,λ2是否存在?是否唯一?
O
A
B
C
M
N
O
A
B
C
M
N
存在
唯一
思考6:若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?
e1
a
a=λ1e1+0e2
e2
a
a=0e1+λ2e2
思考7:根据上述分析,平面内任一向量a都可以由这个平面内两个不共线的向量e1,e2表示出来,从而可形成一个定理.你能完整地描述这个定理的内容吗?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
思考8:上述定理称为平面向量基本定理,不共线向量e1,e2叫做表示这一平面内所有向量的一组基底.
那么同一平面内可以作基底的向量有多少组?不同基底对应向量a的表示式是否相同?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
无数组
不同
不共线
梳理
如果
,
是同一平面内的两个________向量,那么对于
这一平面内的________向量
,存在唯一一对实数
,
使
=________________________________.
(1)平面向量基本定理
(2)基底
平面内________的向量
,
叫作表示这一平面内所有向量的一组基底.
任何一个
不共线
类型一 对基底概念的理解
例1 如果
,
是平面
内两个不共线的向量,那么下列说法中不正确的是( )
(λ,μ∈R)可以表示平面
内的所有向量;
②对于平面
内任一向量
,使
的实数对(λ,μ)有无穷多个;
③若向量
与
共线,则有且只有一个实数λ,使得
;
④若存在实数λ,μ使得
,则λ=μ=0.
A.①②
B.②③
C.③④
D.②
B
题型探究
考查两个向量是否能构成基底,主要看两向量是否非零且不共线.此外,一个平面的基底一旦确定,那么平面上任意一个向量都可以由这个基底唯一线性表示出来.
反思与感悟
跟踪训练1 若
,
是平面内的一组基底,则下列四组向量能作为平面向量的基底的是( )
A.
C.
D.
B.
,
,
,
,
D
类型二 平面向量基本定理的应用
例2.如图所示,在△ABC中,D,F分别是BC,AC的
中点,
,
,
.
用
,
表示向量
,
,
,
,
;
解:
例3 如图所示,在平行四边形
中,
,
分别是
,
边上的中点,若
,
试以
,
为基底表
示
,
.
解
因为在
中,
,
分别是
,
边上的中点,且
,
所以
所以
变式练习
若本例中其他条件不变,设
,
,试以
,
为基底表示
,
.
解
因为
所以,由
解得
将不共线的向量作为基底表示其他向量的方法有两种:
一种是利用向量的线性运算及法则对所求向量不断转化,直至能用基底表示为止;
另一种是列向量方程组,利用基底表示向量的唯一性求解.
反思与感悟
1.下列关于基底的说法正确的是(
)
①平面内不共线的任意两个向量都可作为一组基底;
②基底中的向量可以是零向量;
③平面内的基底一旦确定,该平面内的向量关于基底的线性分解形式也是唯一确定的.
A.①
B.②
C.①③
D.②③
2.如图,已知
,
,
,用
,
表示
,
则等于( )
A.
B.
C.
D.
C
B
当堂练习
3.已知向量
,
不共线,实数
,
满足
,则
=____,
=____.
4.如图所示,在正方形
中,设
,
,
则当以
,
为基底时,
可表示为________
,
当以
,
为基底时,
可表示为________.
-15
-12
课堂小结
1.对基底的理解
(1)基底的特征
基底具备两个主要特征:①基底是两个不共线向量;②基底的选择是不唯一的.平面内两向量不共线是这两个向量可以作为这个平面内所有向量的一组基底的条件.
(2)零向量与任意向量共线,故不能作为基底.
2.准确理解平面向量基本定理
平面向量基本定理的实质是向量的分解,即平面内任一向量都可以沿两个不共线的方向分解成两个向量和的形式,且分解是唯一的.
2.已知在梯形ABCD中,AB∥DC,且AB=2CD,E,F分别是DC,AB的中点,设
,
,试用
,
为基底表示
,
,
.
作业布置
1.教材
,习题2-3
5、6
2.3.2
平面向量基本定理
北师大版
复习回顾
1.
向量加法与减法有哪几种几何运算法则?
2.怎样理解向量的数乘运算
?
λ>0时,
与
方向________
;
λ<0时,
与
方向________
;
λ=0时,
=________
__________
相反
相同
3.平面向量共线定理是什么?
非零向量a与向量b共线
存在唯一实数λ,使b=λa.
知识点 平面向量基本定理
思考1:
如图,已知
,
是两个不共线的确定向量,如何作出和量
?如何作出和量
?
?
e1
e2
e2
o
A
e1
B
e2
O
e2
A
e1
B
C
问题导学
°
思考2:如图,设OA,OB,OC为三条共点射线,P为OC上一点,能否在OA、OB上分别找一点M、N,使四边形OMPN为平行四边形?
M
N
O
A
B
C
P
思考3:在下列两图中向量
,
,
不共线,能否在直线OA、OB上分别找一点M、N,使
?
O
A
B
C
M
N
O
A
B
C
M
N
思考4:在上图中,设
=e1,
=e2,
=a,则向量
、
分别与e1,e2的关系如何?从而向量a与e1,e2的关系如何?
O
A
B
C
M
N
O
A
B
C
M
N
思考5:若上述向量e1,e2,a都为定向量,且e1,e2不共线,则实数λ1,λ2是否存在?是否唯一?
O
A
B
C
M
N
O
A
B
C
M
N
存在
唯一
思考6:若向量a与e1或e2共线,a还能用λ1e1+λ2e2表示吗?
e1
a
a=λ1e1+0e2
e2
a
a=0e1+λ2e2
思考7:根据上述分析,平面内任一向量a都可以由这个平面内两个不共线的向量e1,e2表示出来,从而可形成一个定理.你能完整地描述这个定理的内容吗?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
思考8:上述定理称为平面向量基本定理,不共线向量e1,e2叫做表示这一平面内所有向量的一组基底.
那么同一平面内可以作基底的向量有多少组?不同基底对应向量a的表示式是否相同?
若e1、e2是同一平面内的两个不共线向量,则对于这一平面内的任意向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
无数组
不同
不共线
梳理
如果
,
是同一平面内的两个________向量,那么对于
这一平面内的________向量
,存在唯一一对实数
,
使
=________________________________.
(1)平面向量基本定理
(2)基底
平面内________的向量
,
叫作表示这一平面内所有向量的一组基底.
任何一个
不共线
类型一 对基底概念的理解
例1 如果
,
是平面
内两个不共线的向量,那么下列说法中不正确的是( )
(λ,μ∈R)可以表示平面
内的所有向量;
②对于平面
内任一向量
,使
的实数对(λ,μ)有无穷多个;
③若向量
与
共线,则有且只有一个实数λ,使得
;
④若存在实数λ,μ使得
,则λ=μ=0.
A.①②
B.②③
C.③④
D.②
B
题型探究
考查两个向量是否能构成基底,主要看两向量是否非零且不共线.此外,一个平面的基底一旦确定,那么平面上任意一个向量都可以由这个基底唯一线性表示出来.
反思与感悟
跟踪训练1 若
,
是平面内的一组基底,则下列四组向量能作为平面向量的基底的是( )
A.
C.
D.
B.
,
,
,
,
D
类型二 平面向量基本定理的应用
例2.如图所示,在△ABC中,D,F分别是BC,AC的
中点,
,
,
.
用
,
表示向量
,
,
,
,
;
解:
例3 如图所示,在平行四边形
中,
,
分别是
,
边上的中点,若
,
试以
,
为基底表
示
,
.
解
因为在
中,
,
分别是
,
边上的中点,且
,
所以
所以
变式练习
若本例中其他条件不变,设
,
,试以
,
为基底表示
,
.
解
因为
所以,由
解得
将不共线的向量作为基底表示其他向量的方法有两种:
一种是利用向量的线性运算及法则对所求向量不断转化,直至能用基底表示为止;
另一种是列向量方程组,利用基底表示向量的唯一性求解.
反思与感悟
1.下列关于基底的说法正确的是(
)
①平面内不共线的任意两个向量都可作为一组基底;
②基底中的向量可以是零向量;
③平面内的基底一旦确定,该平面内的向量关于基底的线性分解形式也是唯一确定的.
A.①
B.②
C.①③
D.②③
2.如图,已知
,
,
,用
,
表示
,
则等于( )
A.
B.
C.
D.
C
B
当堂练习
3.已知向量
,
不共线,实数
,
满足
,则
=____,
=____.
4.如图所示,在正方形
中,设
,
,
则当以
,
为基底时,
可表示为________
,
当以
,
为基底时,
可表示为________.
-15
-12
课堂小结
1.对基底的理解
(1)基底的特征
基底具备两个主要特征:①基底是两个不共线向量;②基底的选择是不唯一的.平面内两向量不共线是这两个向量可以作为这个平面内所有向量的一组基底的条件.
(2)零向量与任意向量共线,故不能作为基底.
2.准确理解平面向量基本定理
平面向量基本定理的实质是向量的分解,即平面内任一向量都可以沿两个不共线的方向分解成两个向量和的形式,且分解是唯一的.
2.已知在梯形ABCD中,AB∥DC,且AB=2CD,E,F分别是DC,AB的中点,设
,
,试用
,
为基底表示
,
,
.
作业布置
1.教材
,习题2-3
5、6
