人教版八年级数学上册13.1 轴对称课件(21张ppt)
文档属性
| 名称 | 人教版八年级数学上册13.1 轴对称课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
13.1
轴对称
人民教育出版社义务教育教科书八年级数学(上册)
如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,
那么这个图形叫做轴对称图形,这条直线叫做对称轴。
对称轴
下面的图形都是轴对称图形,请分别找出每个图形的对称轴。
取一张纸,先对折,然后打开放在
桌上,在纸的一侧上滴一滴墨水,将纸
迅速合上、压平,再将纸打开,观察所
得到的图案。
位于折痕两侧的墨迹图案彼此之间
有什么关系?
观察下图中的每组图案,你发现了什么?
如果两个图形沿一条直线对折,它们能
完全重合,那么这两个图形成轴对称,这条
直线就是对称轴。
欣赏下面这幅图,你能找出两个成轴对称的图形吗?
轴对称图形和轴对称是不是一回事?它们
有区别吗?
不同点:轴对称图形对一个图形而言。
成轴对称是对两个图形而言。
联系:
轴对称图形
成轴对称
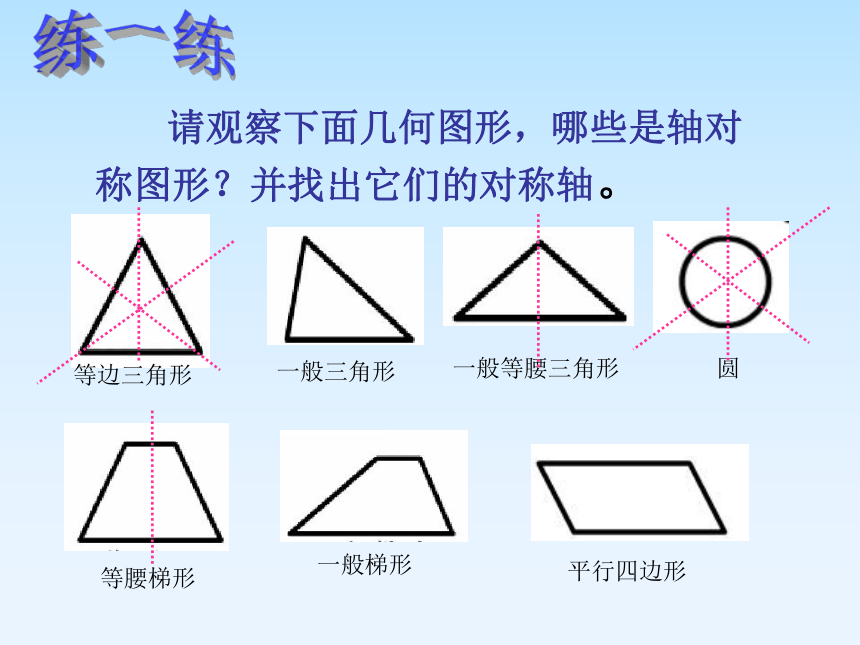
请观察下面几何图形,哪些是轴对称图形?并找出它们的对称轴。
等边三角形
一般三角形
一般等腰三角形
圆
等腰梯形
一般梯形
平行四边形
找出下列图形的对称轴
美国
加拿大
乌拉圭
澳大利亚
国旗是一个国家的象征,观察下面的国旗
哪些是轴对称图形?找出它们的对称轴。
瑞典
英国
以色列
挪威
√
√
√
√
√
√
√
√
下列16个英文字母中,是轴对称图形的是
A B C D E F G H
M N O P Q R S T
A
C
D
E
H
M
O
T
朴素的对称观念在我们的生活中广泛存在:①文学中的对仗也是一种“对称”。王维的诗句“明月松间照,清泉石上流”无非是把第一句中的“明月”变成了第二句中的“清泉”,“松间”变成了“石上”,“照”变成了“流”,词意变了,但是词性和句式结构并没有变.由于工整的文字对仗,使王维诗的自然意境之美得到很好地表现.我国文学中的歌赋尤其是对联,更把“对称”的要求推进到极高的境界.
阅读讨论
对称与文化
②我国人民喜闻乐见的京剧脸谱,多是对称的图形,民族建筑中整体或局部呈对称的现象更是常见.
③对称概念在物理学等领域中也起着重要的作用.著名的物理学家杨振宇和李政道获得的诺贝尔奖研究成果——“宇称不守恒”就和对称密切相关.杨振宇在《对称和物理学》一文中写道:“在理解物理世界的过程中,21世纪会目睹对称概念的新方面吗?我的回答是,十分可能”
。
正如20世纪著名数学家赫尔曼.外尔所说的,“对称是一种思想,通过它,人们毕生追求,并创造次序、美丽和完善……”对称的涵义已远远超出了数学的范畴,它出现在自然、艺术、科学、建筑乃至诗歌
中。对称是一种美,生活有了“对称”
会更美。
M
N
A
B
C
A′
C′
B′
如图,△ABC和
△A'B'C'关于直线MN对称,点A、B、C分别是点A',B',C'的对称点,线段AA'、BB'、CC'与MN有什么关系?
P
点A,A′是对称点,设AA′交对称轴MN于点P,将△ABC和
△A′B′C′沿直线MN折叠后,点A与A′重合,于是有:
AP=PA′,∠MPA=
∠MPA′=90°
对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段。
M
N
Q
p
G
A
B
C
A′
C′
B′
P.
.
Q
定义:
经过线段的中点并且垂直于这条线段的直线,就叫这条线段的垂直平分线,也叫中垂线。
图中的两个三角形关于直线MN对称
Q
p
G
M
N
A
B
C
A'
C′
B′
几何语言:
∵MN是AA′的垂直平分线
∴AP=PA′,
∠MPA=
∠MPA′=90°
轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线。
即对称点的连线被对称轴垂直平分。
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线。
13.1
轴对称
人民教育出版社义务教育教科书八年级数学(上册)
如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,
那么这个图形叫做轴对称图形,这条直线叫做对称轴。
对称轴
下面的图形都是轴对称图形,请分别找出每个图形的对称轴。
取一张纸,先对折,然后打开放在
桌上,在纸的一侧上滴一滴墨水,将纸
迅速合上、压平,再将纸打开,观察所
得到的图案。
位于折痕两侧的墨迹图案彼此之间
有什么关系?
观察下图中的每组图案,你发现了什么?
如果两个图形沿一条直线对折,它们能
完全重合,那么这两个图形成轴对称,这条
直线就是对称轴。
欣赏下面这幅图,你能找出两个成轴对称的图形吗?
轴对称图形和轴对称是不是一回事?它们
有区别吗?
不同点:轴对称图形对一个图形而言。
成轴对称是对两个图形而言。
联系:
轴对称图形
成轴对称
请观察下面几何图形,哪些是轴对称图形?并找出它们的对称轴。
等边三角形
一般三角形
一般等腰三角形
圆
等腰梯形
一般梯形
平行四边形
找出下列图形的对称轴
美国
加拿大
乌拉圭
澳大利亚
国旗是一个国家的象征,观察下面的国旗
哪些是轴对称图形?找出它们的对称轴。
瑞典
英国
以色列
挪威
√
√
√
√
√
√
√
√
下列16个英文字母中,是轴对称图形的是
A B C D E F G H
M N O P Q R S T
A
C
D
E
H
M
O
T
朴素的对称观念在我们的生活中广泛存在:①文学中的对仗也是一种“对称”。王维的诗句“明月松间照,清泉石上流”无非是把第一句中的“明月”变成了第二句中的“清泉”,“松间”变成了“石上”,“照”变成了“流”,词意变了,但是词性和句式结构并没有变.由于工整的文字对仗,使王维诗的自然意境之美得到很好地表现.我国文学中的歌赋尤其是对联,更把“对称”的要求推进到极高的境界.
阅读讨论
对称与文化
②我国人民喜闻乐见的京剧脸谱,多是对称的图形,民族建筑中整体或局部呈对称的现象更是常见.
③对称概念在物理学等领域中也起着重要的作用.著名的物理学家杨振宇和李政道获得的诺贝尔奖研究成果——“宇称不守恒”就和对称密切相关.杨振宇在《对称和物理学》一文中写道:“在理解物理世界的过程中,21世纪会目睹对称概念的新方面吗?我的回答是,十分可能”
。
正如20世纪著名数学家赫尔曼.外尔所说的,“对称是一种思想,通过它,人们毕生追求,并创造次序、美丽和完善……”对称的涵义已远远超出了数学的范畴,它出现在自然、艺术、科学、建筑乃至诗歌
中。对称是一种美,生活有了“对称”
会更美。
M
N
A
B
C
A′
C′
B′
如图,△ABC和
△A'B'C'关于直线MN对称,点A、B、C分别是点A',B',C'的对称点,线段AA'、BB'、CC'与MN有什么关系?
P
点A,A′是对称点,设AA′交对称轴MN于点P,将△ABC和
△A′B′C′沿直线MN折叠后,点A与A′重合,于是有:
AP=PA′,∠MPA=
∠MPA′=90°
对称轴所在的直线经过对称点所连线段的中点,并且垂直于这条线段。
M
N
Q
p
G
A
B
C
A′
C′
B′
P.
.
Q
定义:
经过线段的中点并且垂直于这条线段的直线,就叫这条线段的垂直平分线,也叫中垂线。
图中的两个三角形关于直线MN对称
Q
p
G
M
N
A
B
C
A'
C′
B′
几何语言:
∵MN是AA′的垂直平分线
∴AP=PA′,
∠MPA=
∠MPA′=90°
轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线。
即对称点的连线被对称轴垂直平分。
类似地,轴对称图形的对称轴,是任何一对对称点所连线段的垂直平分线。
