2021--2022学年人教版八年级数学上册11.1.2 三角形的高、中线与角平分线 (共42张ppt)
文档属性
| 名称 | 2021--2022学年人教版八年级数学上册11.1.2 三角形的高、中线与角平分线 (共42张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 00:00:00 | ||
图片预览





文档简介
11.1.2 三角形的高、中线与角平分线
与三角形有关的线段
八年级上册 RJ
初中数学
知识回顾
概念
三角形
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边的和
大于第三边
三角形两边的差
小于第三边
边、顶点、角
1.了解三角形的高、中线和角平分线的定义及画法.
2.会利用三角形的高、中线和角平分线解决实际
问题.
学习目标
定义
图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
复
习
回
顾
你还记得 “过一点画已知直线的垂线” 吗?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画.
过三角形的一个顶点,你能画出它的对边的垂线吗?
想一想
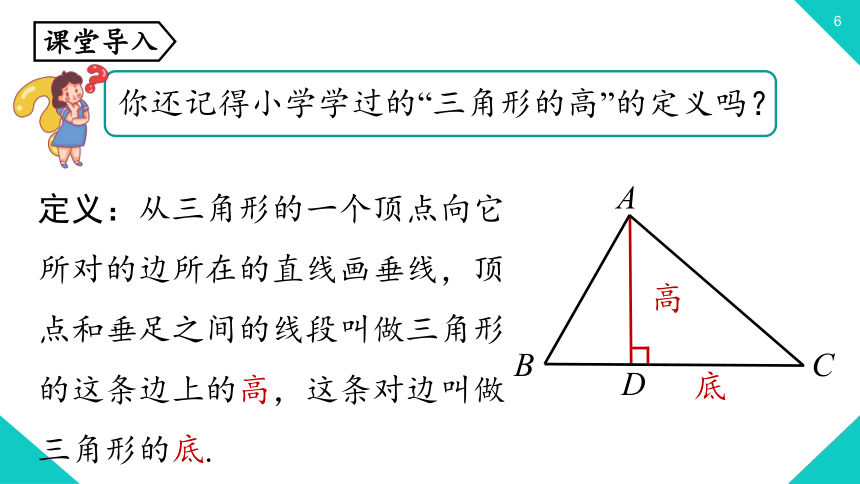
你还记得小学学过的“三角形的高”的定义吗?
定义:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的这条边上的高,这条对边叫做三角形的底.
高
底
A
B
C
课堂导入
D
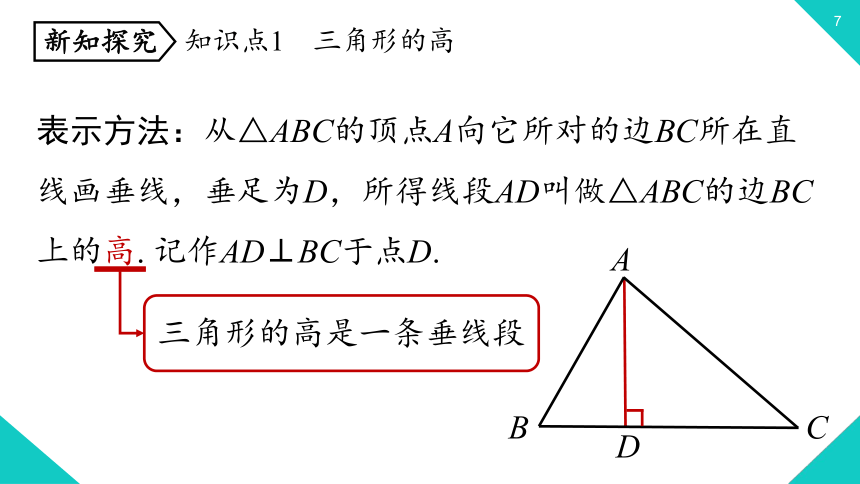
表示方法:从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高. 记作AD⊥BC于点D.
知识点1 三角形的高
新知探究
A
B
C
D
三角形的高是一条垂线段
三角形高的画法:用三角板过某一顶点向其对边或对边所在的直线画垂线,交对边或对边延长线于一点,所得的垂线段就是这条边上的高.
A
B
C
D
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
用同样的方法,你能画出△ABC的另两条边上的高吗?
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
E
F
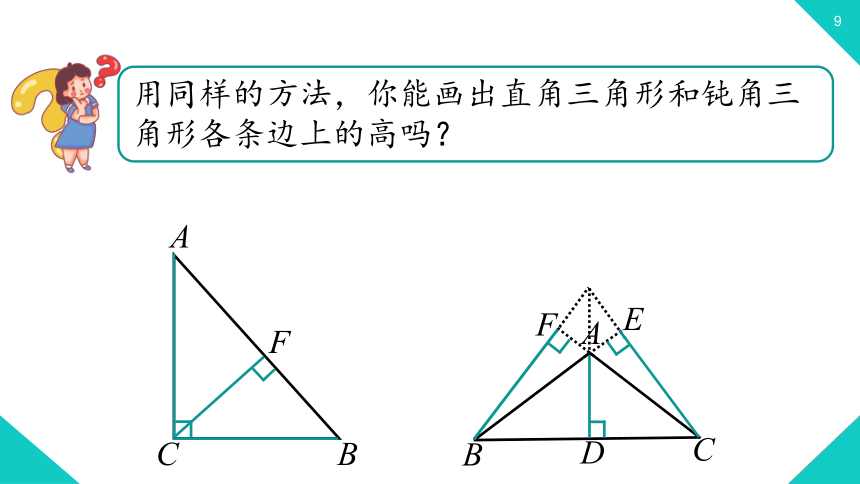
用同样的方法,你能画出直角三角形和钝角三角形各条边上的高吗?
B
A
C
F
A
B
C
D
E
F
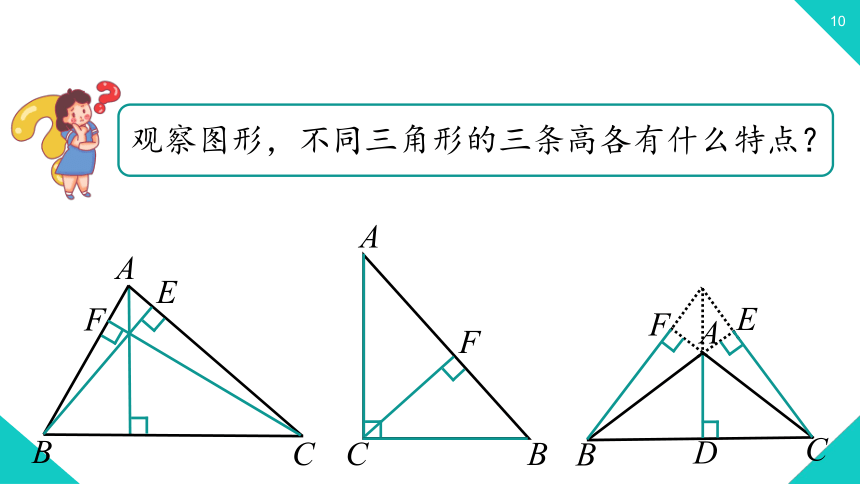
观察图形,不同三角形的三条高各有什么特点?
B
A
C
F
A
B
C
D
E
F
A
B
C
E
F
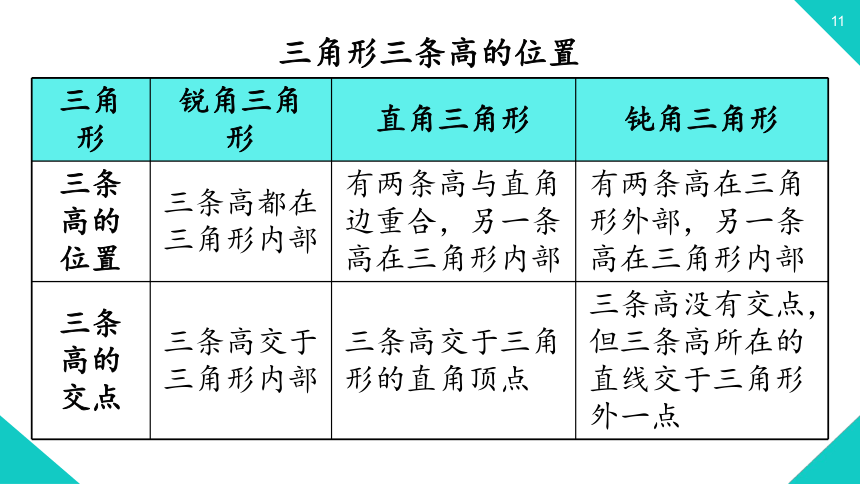
三角形三条高的位置
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}三角形
锐角三角形
直角三角形
钝角三角形
三条高的位置
三条高都在三角形内部
有两条高与直角边重合,另一条高在三角形内部
有两条高在三角形外部,另一条高在三角形内部
三条高的交点
三条高交于三角形内部
三条高交于三角形的直角顶点
三条高没有交点,但三条高所在的直线交于三角形外一点
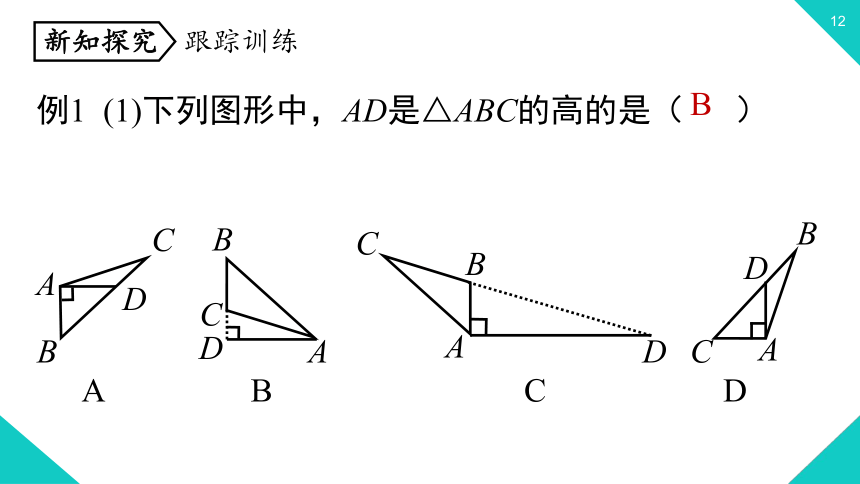
例1 (1)下列图形中,AD是△ABC的高的是( )
B
跟踪训练
新知探究
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
(2) 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
方法总结:可利用面积相等作桥梁(但不求面积)求三角形的高, 此解题方法通常称为“面积法”.
利用三角形的高求值
解析:当BP⊥AC时,BP的值最小.
∵S△ABC= BC·AD,S△ABC= AC·BP,
∴ BC·AD= AC·BP ∴BC·AD=AC·BP
∴6×4=5BP, BP= 所以BP的最小值为
新知探究
跟踪训练
判断一条线段是否为三角形的高的方法
一看顶点:三角形的高一定过顶点.
二看垂足:三角形的高的垂足在顶点的对边或对边延长线上.
例2 .[2021黑龙江齐齐哈尔建华区期末] 如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
跟踪训练
新知探究
三角形的内部
三角形的直角顶点
三角形的外部
2.表示方法:
AD是△ABC的边BC上的中线,
点D是边BC的中点,
BD=CD= BC.
1.定义:连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形的这条边上的中线.
D
C
B
A
知识点2 三角形的中线
新知探究
被三角形的中线分成的两个小三角形的面积大小有什么关系?
D
C
B
A
解:如图,过点A作AE⊥BC,
因为AD是△ABC的边BC上的中线,
所以BD=CD= 12 BC.
所以△ABD的面积为 12 BD×AE,△ACD的面积为 12CD×AE,所以△ABD和△ACD的面积相等.
?
如图,在△ABC中,AD是边BC上的中线,证明:△ABD和△ACD的面积相等.
D
C
B
A
E
三角形的中线将三角形分成面积相等的两个小三角形.
3.画法:
连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
D
C
B
A
E
F
用同样的方法,你能画出△ABC的另两条边上的中线吗?
4.画一画:如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
画图发现
三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
1.定义:在三角形中,连接一个顶点和所对边的中点的线段叫做三角形的中线.
2.三角形的重心:三角形三条中线的交点.
3.三角形的重心在各三角形中的位置:在三角形内部.
4.三角形的任何一条中线把三角形分成面积相等的两个三角形.如上图:AD为中线,则S△ABD=S△ACD.
5.三角形任何一边上的中线把三角形分成的两个小三角形周长之差等于原三角形长边与短边之差.△ABD的周长–△ACD的周长=AB–AC.
归纳总结
新知探究
例 3 如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )
A.19 cm B.22 cm C.25 cm D.31 cm
解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)–(AC+CD+AD)=AB –AC.
∵△ABD的周长为25 cm,AB比AC长6 cm,
∴△ACD的周长为25–6=19(cm).
利用三角形的中线求线段的值
素养考点 3
A
新知探究
如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE ,AE=_____;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .
(3)若AB=4,AC=3,则△ABD的周长与△ACD的周长之差是___.
2
BD
6 cm?
A
B
C
D
E
F
G
EC
1
巩固练习
例4 (1)如图,有一块三角形菜地,现要将其分成面积比为1∶1∶2的三块,已知点A处是三块菜地的共同水源处,则三块菜地应该怎么分?
解:根据面积比为1∶1∶2的要求,
可以将三角形菜地的总面积看作4份.
如图,作△ABC的中线AD,△ABD的中线AE,
所得到的△ABE,△AED,△ADC的面积比就是1∶1∶2.
A
B
C
E
D
新知探究
三角形的中线可以将三角形分成面积相等的两个小三角形
利用三角形的中线面积问题
(2):如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
解:∵点D是AC的中点,∴AD= AC.
∵S△ABC=12,∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,∴S△ABE= S△ABC= ×12=4.
新知探究
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
新知探究
问题1 如图,若OC是∠AOB的平分线,你能得到什么结论?
A
C
B
O
∠AOC= ∠BOC
问题2 你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
A
B
C
D
想一想:三角形的角平分线与角的角平分线相同吗?
相同点是: ∠ABD= ∠ CBD;
不同点是:前者是线段,后者是射线.
新知探究
知识点3 三角形的角平分线
1.定义:在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
2.表示方法:AD是△ABC的角平分线,
AD平分∠BAC,交BC于点D,
∠BAD=∠CAD= 12 ∠BAC.
?
D
B
C
A
知识点3 三角形的角平分线
新知探究
3.画法:画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线.
用同样的方法,你能画出△ABC的另外两条角平分线吗?
D
B
C
A
E
F
观察三条角平分线,你有什么发现?
三角形的三条角平分线都在三角形的内部,并且三条角平分线交于三角形内一点.
例5 (1)如图,AD,BE,CF分别是△ABC的三条角平分线,请根据图中各角之间的关系填空:
D
A
B
C
E
F
1
2
3
4
(1)∠1=∠( );
(2)∠3= ( );
(3)∠ACB=( )∠4.
2
∠ABC
2
新知探究
利用三角形的角平分线求角的度数
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°–∠B–∠BAD
=180°–36°–34°
=110°.
(2) 如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
探究新知
三角形的
重要线段
概念
图形
表示法
数量及交点位置
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的高线.
∴AD⊥BC,∠ADB=∠ADC=90°.
3条高,锐角三角形:形内;钝角三角形:形外;直角三角形:直角顶点
三角形
的中线
三角形中,连结一个顶点和它对边中的线段
3条,交点叫作三角形的重心.形内
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
3条,形内.
课堂小结
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
1.如图,在△ABC中,∠1=∠2=∠3=∠4,则下列说法中,正确的是( )
A.AD是△ABE的中线
B.AE是△ABC的角平分线
C.AF是△ACE的高线
D.AE是△ABC的中线
B
A
B
C
D
E
F
1
2
3
4
随堂练习
∠1+∠2=∠3+∠4
2.如图,在△ABC中,AE是中线,AD是角平分线,AF是高,填空:
(1)BE=( )= 12 ( );
(2)∠BAD=( )= 12 ( );
(3)∠AFB=( )=90°;
?
CE
BC
∠CAD
∠BAC
∠CFA
B
C
D
E
A
F
解:因为AE为中线,
所以 BC=2BE=16.
因为AF为高,
所以∠AFB=∠CFA=90°.
所以△ABC的面积为 12 ×16×7=56.
?
B
C
D
E
A
F
(4)当BE=8,AF=7时,求△ABC的面积.
思路引导:
3.如图所示,已知△ABC的周长为27 cm,
AC=9 cm,BC边上的中线AD为6 cm,△ABD
的周长为19 cm,AB= .
8 cm
C
A
D
B
AB+BC+AC=
27 cm,AC=9 cm
AB+BD+AD=
19 cm,AD=6 cm
AB+BC=18 cm
AB+BD=13 cm
AB=8 cm
BC=2BD
1.(2021?重庆江津区校级期中)如图,在△ABC中,AD是边BC上的高,AE是角平分线. 若∠B=80°,∠C=30°,求∠DAE.
拓展提升
D
E
B
A
C
解:∵在△ABC中, ∠B=80°∠C=30°,
∴∠BAC=70°.
∵AE是角平分线,
∴∠BAE= 12 ∠BAC=35°.
?
1.(2021?重庆江津区校级期中)如图,在△ABC中,AD是边BC上的高,AE是角平分线. 若∠B=80°,∠C=30°,求∠DAE.
拓展提升
D
E
B
A
C
∵AD是边BC上的高,
∴∠BAD=90°-∠B=10°,
∴∠DAE=∠BAE-∠BAD=35°-
10°=25°.
2.[2021四川绵阳东辰国际学校月考]如图,在△ABC中,已知D,E,F分别为BC,AD,CE的中点,且S△ABC=8 cm2,则图中阴影部分的面积等于 ( )
A.1 cm2 B.2 cm2
C.4 cm2 D.6 cm2
【解析】 ∵E是AD的中点,∴S△ABE=12S△ABD,S△ACE=12S△ADC,
∴S△ABE+S△ACE=12S△ABC=12×8=4(cm2),
∴S△BCE=8-4= 4(cm2).∵F是CE的中点,∴S△BEF=12S△BCE=12×4=2(cm2),
故题图中阴影部分的面积为2 cm2.故选B.
?
3.易错题[2021重庆期末]如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF⊥AD于点H,则下列说法正确的有 ( )
①AD是△ABE的角平分线;
②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;
④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
【解析】 由∠1=∠2,知AG是△ABE的角平分线,故①错误;由G为AD的中点,知BG是△ABD的边AD上的中线,故②错误;由CH⊥AD于点H,知CH是△ACD的边AD上的高,故③正确;由∠1=∠2,AH⊥CF于点H,知AH是△ACF的角平分线和高,故④正确.故选B.
与三角形有关的线段
八年级上册 RJ
初中数学
知识回顾
概念
三角形
三角形的分类
三角形的三边关系
按角分类
按边分类
三角形两边的和
大于第三边
三角形两边的差
小于第三边
边、顶点、角
1.了解三角形的高、中线和角平分线的定义及画法.
2.会利用三角形的高、中线和角平分线解决实际
问题.
学习目标
定义
图示
垂线
线段中点
角平分线
O
B
A
A
B
当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线
把一条线段分成两条相等的线段的点
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线
复
习
回
顾
你还记得 “过一点画已知直线的垂线” 吗?
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
放、
靠、
过、
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画.
过三角形的一个顶点,你能画出它的对边的垂线吗?
想一想
你还记得小学学过的“三角形的高”的定义吗?
定义:从三角形的一个顶点向它所对的边所在的直线画垂线,顶点和垂足之间的线段叫做三角形的这条边上的高,这条对边叫做三角形的底.
高
底
A
B
C
课堂导入
D
表示方法:从△ABC的顶点A向它所对的边BC所在直线画垂线,垂足为D,所得线段AD叫做△ABC的边BC上的高. 记作AD⊥BC于点D.
知识点1 三角形的高
新知探究
A
B
C
D
三角形的高是一条垂线段
三角形高的画法:用三角板过某一顶点向其对边或对边所在的直线画垂线,交对边或对边延长线于一点,所得的垂线段就是这条边上的高.
A
B
C
D
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
用同样的方法,你能画出△ABC的另两条边上的高吗?
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
E
F
用同样的方法,你能画出直角三角形和钝角三角形各条边上的高吗?
B
A
C
F
A
B
C
D
E
F
观察图形,不同三角形的三条高各有什么特点?
B
A
C
F
A
B
C
D
E
F
A
B
C
E
F
三角形三条高的位置
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}三角形
锐角三角形
直角三角形
钝角三角形
三条高的位置
三条高都在三角形内部
有两条高与直角边重合,另一条高在三角形内部
有两条高在三角形外部,另一条高在三角形内部
三条高的交点
三条高交于三角形内部
三条高交于三角形的直角顶点
三条高没有交点,但三条高所在的直线交于三角形外一点
例1 (1)下列图形中,AD是△ABC的高的是( )
B
跟踪训练
新知探究
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
(2) 如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为____.
方法总结:可利用面积相等作桥梁(但不求面积)求三角形的高, 此解题方法通常称为“面积法”.
利用三角形的高求值
解析:当BP⊥AC时,BP的值最小.
∵S△ABC= BC·AD,S△ABC= AC·BP,
∴ BC·AD= AC·BP ∴BC·AD=AC·BP
∴6×4=5BP, BP= 所以BP的最小值为
新知探究
跟踪训练
判断一条线段是否为三角形的高的方法
一看顶点:三角形的高一定过顶点.
二看垂足:三角形的高的垂足在顶点的对边或对边延长线上.
例2 .[2021黑龙江齐齐哈尔建华区期末] 如果一个三角形的三条高的交点恰好是三角形的一个顶点,那么这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
跟踪训练
新知探究
三角形的内部
三角形的直角顶点
三角形的外部
2.表示方法:
AD是△ABC的边BC上的中线,
点D是边BC的中点,
BD=CD= BC.
1.定义:连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形的这条边上的中线.
D
C
B
A
知识点2 三角形的中线
新知探究
被三角形的中线分成的两个小三角形的面积大小有什么关系?
D
C
B
A
解:如图,过点A作AE⊥BC,
因为AD是△ABC的边BC上的中线,
所以BD=CD= 12 BC.
所以△ABD的面积为 12 BD×AE,△ACD的面积为 12CD×AE,所以△ABD和△ACD的面积相等.
?
如图,在△ABC中,AD是边BC上的中线,证明:△ABD和△ACD的面积相等.
D
C
B
A
E
三角形的中线将三角形分成面积相等的两个小三角形.
3.画法:
连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
D
C
B
A
E
F
用同样的方法,你能画出△ABC的另两条边上的中线吗?
4.画一画:如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
画图发现
三角形的三条中线交于三角形内部一点.这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
1.定义:在三角形中,连接一个顶点和所对边的中点的线段叫做三角形的中线.
2.三角形的重心:三角形三条中线的交点.
3.三角形的重心在各三角形中的位置:在三角形内部.
4.三角形的任何一条中线把三角形分成面积相等的两个三角形.如上图:AD为中线,则S△ABD=S△ACD.
5.三角形任何一边上的中线把三角形分成的两个小三角形周长之差等于原三角形长边与短边之差.△ABD的周长–△ACD的周长=AB–AC.
归纳总结
新知探究
例 3 如图所示,AD是△ABC的中线,已知△ABD的周长为25 cm,AB比AC长6 cm,则△ACD的周长为( )
A.19 cm B.22 cm C.25 cm D.31 cm
解:∵AD是BC边上的中线,
∴BD=CD,
∴△ABD和△ACD周长的差=(AB+BD+AD)–(AC+CD+AD)=AB –AC.
∵△ABD的周长为25 cm,AB比AC长6 cm,
∴△ACD的周长为25–6=19(cm).
利用三角形的中线求线段的值
素养考点 3
A
新知探究
如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = AE ,AE=_____;
CD = ;
AF = AB;
(2)若S△ABC = 12 cm2,
则S△ABD = .
(3)若AB=4,AC=3,则△ABD的周长与△ACD的周长之差是___.
2
BD
6 cm?
A
B
C
D
E
F
G
EC
1
巩固练习
例4 (1)如图,有一块三角形菜地,现要将其分成面积比为1∶1∶2的三块,已知点A处是三块菜地的共同水源处,则三块菜地应该怎么分?
解:根据面积比为1∶1∶2的要求,
可以将三角形菜地的总面积看作4份.
如图,作△ABC的中线AD,△ABD的中线AE,
所得到的△ABE,△AED,△ADC的面积比就是1∶1∶2.
A
B
C
E
D
新知探究
三角形的中线可以将三角形分成面积相等的两个小三角形
利用三角形的中线面积问题
(2):如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,求S△ADF-S△BEF的值.
解:∵点D是AC的中点,∴AD= AC.
∵S△ABC=12,∴S△ABD= S△ABC= ×12=6.
∵EC=2BE,S△ABC=12,∴S△ABE= S△ABC= ×12=4.
新知探究
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.
新知探究
问题1 如图,若OC是∠AOB的平分线,你能得到什么结论?
A
C
B
O
∠AOC= ∠BOC
问题2 你能用同样的方法画出任意一个三角形的一个内角的平分线吗?
A
B
C
D
想一想:三角形的角平分线与角的角平分线相同吗?
相同点是: ∠ABD= ∠ CBD;
不同点是:前者是线段,后者是射线.
新知探究
知识点3 三角形的角平分线
1.定义:在三角形中,一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
2.表示方法:AD是△ABC的角平分线,
AD平分∠BAC,交BC于点D,
∠BAD=∠CAD= 12 ∠BAC.
?
D
B
C
A
知识点3 三角形的角平分线
新知探究
3.画法:画∠A的平分线AD,交∠A所对的边BC于点D,所得线段AD叫做△ABC的角平分线.
用同样的方法,你能画出△ABC的另外两条角平分线吗?
D
B
C
A
E
F
观察三条角平分线,你有什么发现?
三角形的三条角平分线都在三角形的内部,并且三条角平分线交于三角形内一点.
例5 (1)如图,AD,BE,CF分别是△ABC的三条角平分线,请根据图中各角之间的关系填空:
D
A
B
C
E
F
1
2
3
4
(1)∠1=∠( );
(2)∠3= ( );
(3)∠ACB=( )∠4.
2
∠ABC
2
新知探究
利用三角形的角平分线求角的度数
解:∵AD是△ABC的角平分线,∠BAC=68°,
∴∠DAC=∠BAD=34°.
在△ABD中,∠B+∠ADB+∠BAD=180°,
∴∠ADB=180°–∠B–∠BAD
=180°–36°–34°
=110°.
(2) 如图,在△ABC中,∠BAC=68°,∠B=36°,AD是△ABC的一条角平分线,求∠ADB的度数.
A
B
D
C
探究新知
三角形的
重要线段
概念
图形
表示法
数量及交点位置
三角形
的高线
从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段
∵AD是△ABC的高线.
∴AD⊥BC,∠ADB=∠ADC=90°.
3条高,锐角三角形:形内;钝角三角形:形外;直角三角形:直角顶点
三角形
的中线
三角形中,连结一个顶点和它对边中的线段
3条,交点叫作三角形的重心.形内
三角形的
角平分线
三角形一个内角的平分线与它的对边相交,这个角顶点与交点之间的线段
3条,形内.
课堂小结
三角形重要线段
高
钝角三角形两短边上的高的画法
中线
会把原三角形面积平分
一边上的中线把原三角形分成两个三角形,这两个三角形的周长差等于原三角形其余两边的差
角平分线
1.如图,在△ABC中,∠1=∠2=∠3=∠4,则下列说法中,正确的是( )
A.AD是△ABE的中线
B.AE是△ABC的角平分线
C.AF是△ACE的高线
D.AE是△ABC的中线
B
A
B
C
D
E
F
1
2
3
4
随堂练习
∠1+∠2=∠3+∠4
2.如图,在△ABC中,AE是中线,AD是角平分线,AF是高,填空:
(1)BE=( )= 12 ( );
(2)∠BAD=( )= 12 ( );
(3)∠AFB=( )=90°;
?
CE
BC
∠CAD
∠BAC
∠CFA
B
C
D
E
A
F
解:因为AE为中线,
所以 BC=2BE=16.
因为AF为高,
所以∠AFB=∠CFA=90°.
所以△ABC的面积为 12 ×16×7=56.
?
B
C
D
E
A
F
(4)当BE=8,AF=7时,求△ABC的面积.
思路引导:
3.如图所示,已知△ABC的周长为27 cm,
AC=9 cm,BC边上的中线AD为6 cm,△ABD
的周长为19 cm,AB= .
8 cm
C
A
D
B
AB+BC+AC=
27 cm,AC=9 cm
AB+BD+AD=
19 cm,AD=6 cm
AB+BC=18 cm
AB+BD=13 cm
AB=8 cm
BC=2BD
1.(2021?重庆江津区校级期中)如图,在△ABC中,AD是边BC上的高,AE是角平分线. 若∠B=80°,∠C=30°,求∠DAE.
拓展提升
D
E
B
A
C
解:∵在△ABC中, ∠B=80°∠C=30°,
∴∠BAC=70°.
∵AE是角平分线,
∴∠BAE= 12 ∠BAC=35°.
?
1.(2021?重庆江津区校级期中)如图,在△ABC中,AD是边BC上的高,AE是角平分线. 若∠B=80°,∠C=30°,求∠DAE.
拓展提升
D
E
B
A
C
∵AD是边BC上的高,
∴∠BAD=90°-∠B=10°,
∴∠DAE=∠BAE-∠BAD=35°-
10°=25°.
2.[2021四川绵阳东辰国际学校月考]如图,在△ABC中,已知D,E,F分别为BC,AD,CE的中点,且S△ABC=8 cm2,则图中阴影部分的面积等于 ( )
A.1 cm2 B.2 cm2
C.4 cm2 D.6 cm2
【解析】 ∵E是AD的中点,∴S△ABE=12S△ABD,S△ACE=12S△ADC,
∴S△ABE+S△ACE=12S△ABC=12×8=4(cm2),
∴S△BCE=8-4= 4(cm2).∵F是CE的中点,∴S△BEF=12S△BCE=12×4=2(cm2),
故题图中阴影部分的面积为2 cm2.故选B.
?
3.易错题[2021重庆期末]如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF⊥AD于点H,则下列说法正确的有 ( )
①AD是△ABE的角平分线;
②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;
④AH是△ACF的角平分线和高.
A.1个 B.2个 C.3个 D.4个
【解析】 由∠1=∠2,知AG是△ABE的角平分线,故①错误;由G为AD的中点,知BG是△ABD的边AD上的中线,故②错误;由CH⊥AD于点H,知CH是△ACD的边AD上的高,故③正确;由∠1=∠2,AH⊥CF于点H,知AH是△ACF的角平分线和高,故④正确.故选B.
