2021--2022学年人教版八年级数学上册11.2.2 三角形的外角(共34张ppt)
文档属性
| 名称 | 2021--2022学年人教版八年级数学上册11.2.2 三角形的外角(共34张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 537.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 11:16:31 | ||
图片预览






文档简介
11.2.2 三角形的外角
与三角形有关的角
八年级上册 RJ
初中数学
1.三角形内角和定理:三角形三个内角的和等于180°.
2.直角三角形的两个锐角互余.
3.有两个角互余的三角形是直角三角形.
练习:1.在△ABC中,∠A=30°,∠B=∠C,则
∠B=_____.
2.在Rt△ABC中,锐角∠B=45°,则另一个锐角∠C=____ .
75°
45°
知识回顾
1.了解三角形外角的概念.
2.理解三角形外角性质及三角形外角和的探究.
3.熟练掌握并运用三角形外角性质解决实际问题.
学习目标
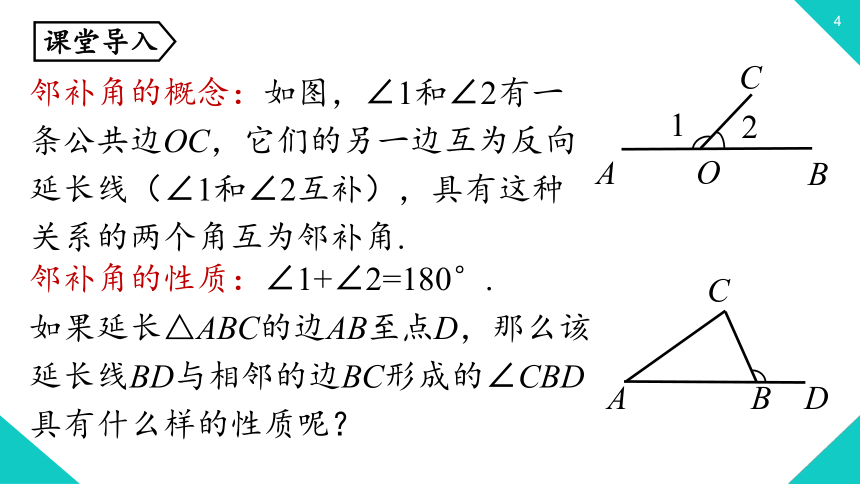
邻补角的概念:如图,∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角互为邻补角.
邻补角的性质:∠1+∠2=180°.
C
A
B
O
1
2
如果延长△ABC的边AB至点D,那么该延长线BD与相邻的边BC形成的∠CBD具有什么样的性质呢?
B
C
A
D
课堂导入
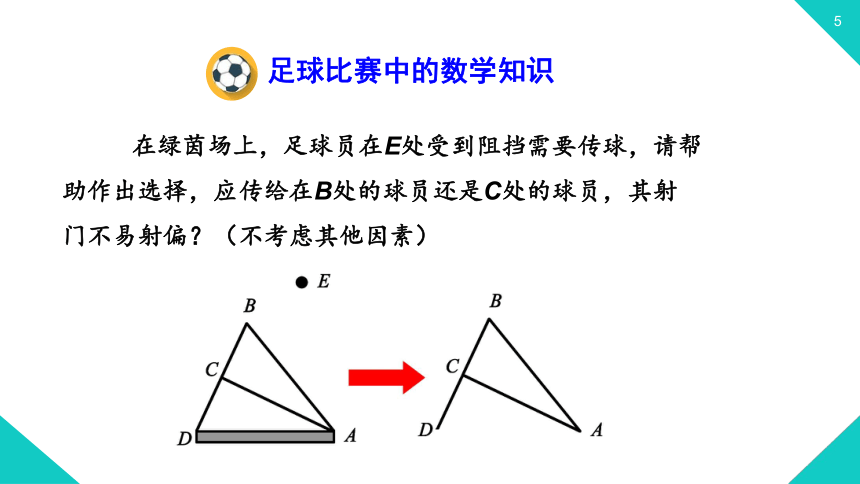
足球比赛中的数学知识
在绿茵场上,足球员在E处受到阻挡需要传球,请帮
助作出选择,应传给在B处的球员还是C处的球员,其射
门不易射偏?(不考虑其他因素)
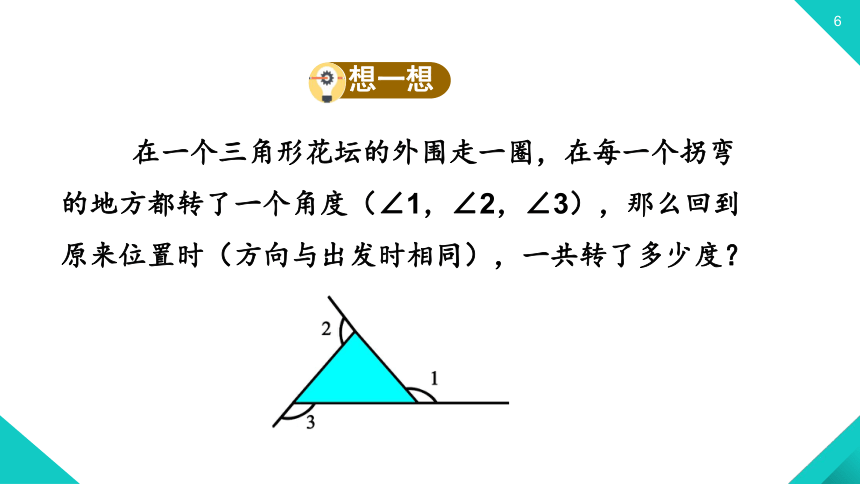
在一个三角形花坛的外围走一圈,在每一个拐弯
的地方都转了一个角度(∠1,∠2,∠3),那么回到
原来位置时(方向与出发时相同),一共转了多少度?
想一想
概念:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.如图,∠CBD是△ABC的一个外角.
问题1:三角形的外角和相邻的内角之间的大小关系?
问题2:三角形的外角具备什么特征?
问题3:三角形共有几个外角?每个顶
点处有几个外角?
三角形的外角
B
C
A
D
知识点1 三角形的外角
新知探究
答案1:三角形的外角和相邻的内角之和为180°.
答案2:三角形的外角具备3个特征:
①顶点在三角形的一个顶点上;
②一条边是三角形的一条边;
③另外一条边是三角形某条边的延长线.
答案3:三角形共有6个外角.每个顶点处有2个外角.
A
B
E
F
C
三角形的外角
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外角,请问∠CAD与∠2,∠3之间的大小关系?
A
B
E
F
C
D
1
2
3
解:∵∠CAD是△ABC的外角,
∠ CAD+∠1=180°,则∠1=180°-∠CAD.
∵∠1,∠2,∠3是△ABC的三个内角,
∴∠1+∠2+∠3=180°,
则∠1=180°-(∠2+∠3).
∴∠CAD=∠2+∠3.
知识点2 三角形外角的性质
新知探究
你能用作平行线的方法证明此结论吗?
D
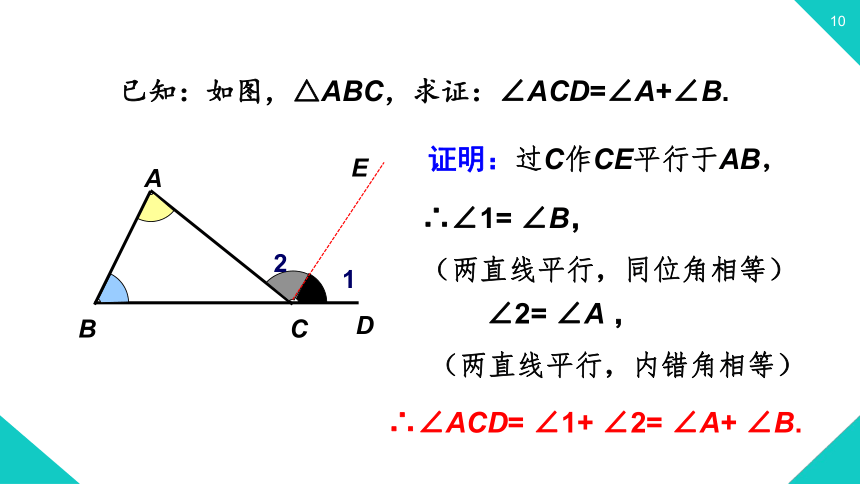
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
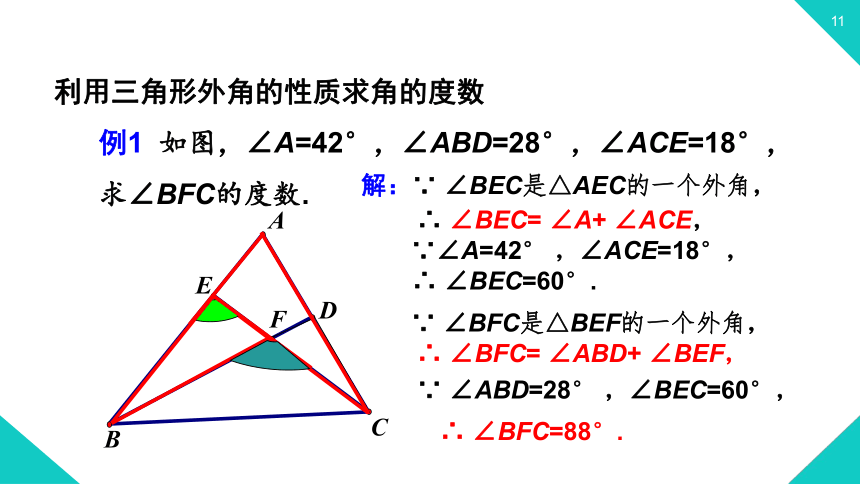
例1 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
利用三角形外角的性质求角的度数
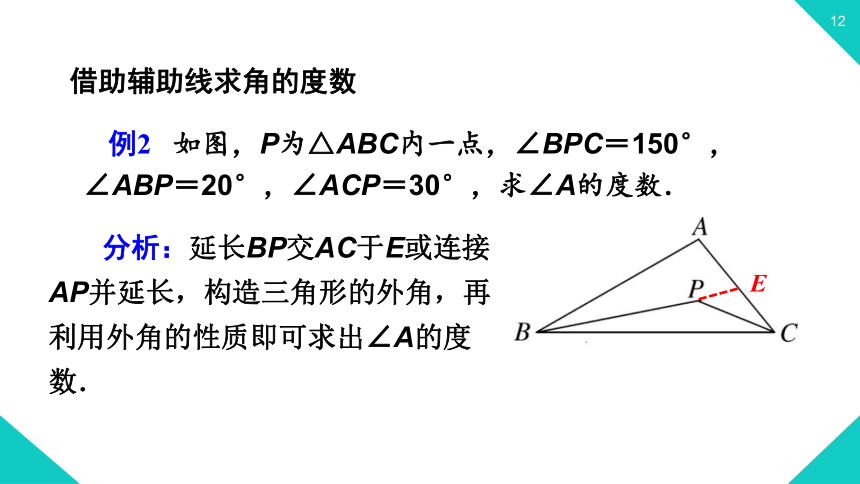
例2 如图,P为△ABC内一点,∠BPC=150°, ∠ABP=20°,∠ACP=30°,求∠A的度数.
分析:延长BP交AC于E或连接AP并延长,构造三角形的外角,再利用外角的性质即可求出∠A的度数.
E
借助辅助线求角的度数
解:延长BP交AC于点E,
则∠BPC,∠PEC分别为△PCE,△ABE的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A,
∴∠PEC=∠BPC-∠PCE
=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
方法点拨:求角的度数,常连接并延长或延长三角形的边长,通过构造三角形的外角,利用外角的性质解决.
【变式题】 (一题多解)如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
E
)
)
1
2
)
3
)
4
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法三:延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外
角,请问∠CAD,∠CBE,∠BCF之间的
大小关系?
∴∠CAD+∠CBE+∠BCF=
(∠2+∠3)+(∠1+∠3)+(∠1+∠2)=
2(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠CAD+∠CBE+∠BCF=360°.
有其他解法吗?
知识点3 三角形的外角和定理
新知探究
A
B
E
F
C
D
1
2
3
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外
角,请问∠CAD,∠CBE,∠BCF之间的
大小关系?
知识点3 三角形的外角和定理
新知探究
A
B
E
F
C
D
1
2
3
方法二 解:∵∠CAD,∠CBE,∠BCF是△ABC
的外角,
∴∠CAD+∠1=180°,则∠CAD=180°-∠1,∠CBE+∠2=180°,则∠CBE=180°-∠2, ∠BCF+∠3=180°,则∠BCF=180°-∠3.
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外
角,请问∠CAD,∠CBE,∠BCF之间的
大小关系?
知识点3 三角形的外角和定理
新知探究
A
B
E
F
C
D
1
2
3
∵∠1,∠2,∠3是△ABC的三个内角,∴∠1+∠2+∠3=180°.
∴∠CAD+∠CBE+∠BCF=(180°-∠1)+(180°-
∠2)+(180°-∠3)=540°-(∠1+∠2+∠3)=360°.
解法三:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
【思考】你能总结出三角形的外角和的数量关系吗?
D
E
F
新知探究
推论:三角形的三个外角和等于360°.
三角形的每一个顶点处各有两个外角,三角形的外角和不是指六个外角的总和,而是说在三角形的每一个顶点处取一个外角,三个不同顶点处的外角和叫做三角形的外角和.
数学语言表示:
如图所示,∠CAD+∠CBE+∠BCF=360°.
三角形的外角和定理
A
B
E
F
C
D
1
2
3
例5 试说出下列图形中∠1和∠2的度数.
解:(1)∠1=180°-80°-60°=40°,∠2=80°+60°=140°.
(2)∠1=180°-30°-40°=110°,∠2=30°+40°=70°.
(3)∠1=90°-40°=50°,∠2=50°+90°=140°.
60?
80?
1
2
(1)
A
B
C
30?
40?
1
2
(2)
A
B
C
40?
2
1
┌
(3)
A
B
C
跟踪训练
新知探究
1.判断下列观点是否正确.
(1)三角形的外角都是钝角. ( )
(2)三角形的外角大于任何一个内角. ( )
(3)三角形的外角等于它的两个内角的和. ( )
(4)三角形的外角和等于360°. ( )
解:(1)三角形的外角是锐角、钝角或者直角.
(2)三角形的外角大于任何一个不相邻内角.
(3)三角形的外角等于它的不相邻两个内角的和.
随堂练习
解:∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∵∠ADC是△ABD的外角, ∴∠ADC=∠1+∠2=90°.
∵∠1=∠2,∴∠1=∠2=45°.
2.如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数.
B
A
D
C
2
1
┐
∵∠ADB是△ACD的外角,
∴∠ADB=∠DAC+∠C=90°.
∵∠C=65°,
∴∠DAC=90°-∠C=25°.
则∠BAC=∠1+∠DAC=70°.
2.如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数.
B
A
D
C
2
1
┐
3.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
解析:∵∠A=60°,∠B=40°,
∴∠ACD=∠A+∠B=100°.
∵CE平分∠ACD,
∴∠ECD=50°.
A
B
C
D
E
C
4.小明把一副含有45°、30°的直角三角板如图摆放,若∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
解析:∵∠α、∠β是三角形的外角,
∴∠α=∠1+∠D,∠β=∠2+∠F.
∵∠1=∠3,∠2=∠4,
∴∠α+∠β=∠1+∠D+∠2+
∠F =∠3+∠4+∠D+∠ =210°.
B
E
B
C
A
F
D
α
β
1
2
3
4
三角形的外角
定义
性质
三角形
外角和
三角形的外角和等于360°
角的一边必须是三角形的一边,另一边必须是三角形的另一边的延长线
三角形的一个外角等于与其不相邻的两个内角的和
课堂小结
1.[2021广东汕头潮阳区期中]如图,在△ABC中,将△ABC沿直线m翻折,点B落在点D的位置,若∠1-∠2=60°,则∠B的度数是 .?
【解析】 如图,∵将△ABC沿直线m翻折,点B落在点D的位置,∠D=∠B,由三角形外角的性质,得∠1=∠B+∠3,∠3=∠2+∠D,∴∠1=∠2+∠D+∠B=∠2+2∠B, ∴∠1-∠2=2∠B=60°,∴∠B=30°.
拓展提升
2.已知五角星如图所示,求∠A+∠B+∠C+∠D+∠E的度数.
分析:利用三角形内角和定理和三角形外角的性质,
将∠A,∠B,∠C,∠D,∠E转化在同一个三角形中.仔细观察五角星,并在五角星中构建出△BGD和△CFE.
C
A
B
E
F
G
D
拓展提升
解:∵在△BGD中,∠AGF是它的外角,
∴∠AGF=∠B+∠D.
∵在△CFE中,∠AFG是它的外角,
∴∠AFG=∠C+∠E.
∵在△AFG中,∠A、∠AFG、∠AGF是三个内角,
∴∠A+∠AFG+∠AGF=180°,
则∠A+∠B+∠C+∠D+∠E=180°.
C
A
B
E
F
G
D
3.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数.
【解析】 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=(∠A+∠H)+(∠B+∠C)+ (∠D+∠E)+(∠F+∠G)=∠1+∠2+∠3+∠4=360°.
4.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求证∠BAC=∠B+2∠E.
B
A
C
D
E
分析:利用角平分线的性质可以得出2倍
的数量关系的角.利用三角形外角性质,
将外角转化为两个不相邻内角的和.
将2倍数量关系的角和外角进行等量转化,即可得出
题目所要证明的结果.
证明:∵∠ECD是△EBC的外角,
∴∠ECD=∠B+∠E.
∵∠BAC是△ACE的外角,
∴∠BAC=∠E+∠ACE.
∵CE是∠ACD的角平分线,
∴∠ACE=∠ECD=∠B+∠E.
∴∠BAC=∠E+∠ACE=∠E+∠B+∠E=∠B+2∠E.
B
A
C
D
E
与三角形有关的角
八年级上册 RJ
初中数学
1.三角形内角和定理:三角形三个内角的和等于180°.
2.直角三角形的两个锐角互余.
3.有两个角互余的三角形是直角三角形.
练习:1.在△ABC中,∠A=30°,∠B=∠C,则
∠B=_____.
2.在Rt△ABC中,锐角∠B=45°,则另一个锐角∠C=____ .
75°
45°
知识回顾
1.了解三角形外角的概念.
2.理解三角形外角性质及三角形外角和的探究.
3.熟练掌握并运用三角形外角性质解决实际问题.
学习目标
邻补角的概念:如图,∠1和∠2有一条公共边OC,它们的另一边互为反向延长线(∠1和∠2互补),具有这种关系的两个角互为邻补角.
邻补角的性质:∠1+∠2=180°.
C
A
B
O
1
2
如果延长△ABC的边AB至点D,那么该延长线BD与相邻的边BC形成的∠CBD具有什么样的性质呢?
B
C
A
D
课堂导入
足球比赛中的数学知识
在绿茵场上,足球员在E处受到阻挡需要传球,请帮
助作出选择,应传给在B处的球员还是C处的球员,其射
门不易射偏?(不考虑其他因素)
在一个三角形花坛的外围走一圈,在每一个拐弯
的地方都转了一个角度(∠1,∠2,∠3),那么回到
原来位置时(方向与出发时相同),一共转了多少度?
想一想
概念:三角形的一边与另一边的延长线组成的角,叫做三角形的外角.如图,∠CBD是△ABC的一个外角.
问题1:三角形的外角和相邻的内角之间的大小关系?
问题2:三角形的外角具备什么特征?
问题3:三角形共有几个外角?每个顶
点处有几个外角?
三角形的外角
B
C
A
D
知识点1 三角形的外角
新知探究
答案1:三角形的外角和相邻的内角之和为180°.
答案2:三角形的外角具备3个特征:
①顶点在三角形的一个顶点上;
②一条边是三角形的一条边;
③另外一条边是三角形某条边的延长线.
答案3:三角形共有6个外角.每个顶点处有2个外角.
A
B
E
F
C
三角形的外角
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外角,请问∠CAD与∠2,∠3之间的大小关系?
A
B
E
F
C
D
1
2
3
解:∵∠CAD是△ABC的外角,
∠ CAD+∠1=180°,则∠1=180°-∠CAD.
∵∠1,∠2,∠3是△ABC的三个内角,
∴∠1+∠2+∠3=180°,
则∠1=180°-(∠2+∠3).
∴∠CAD=∠2+∠3.
知识点2 三角形外角的性质
新知探究
你能用作平行线的方法证明此结论吗?
D
证明:过C作CE平行于AB,
A
B
C
1
2
∴∠1= ∠B,
(两直线平行,同位角相等)
∠2= ∠A ,
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B.
E
已知:如图,△ABC,求证:∠ACD=∠A+∠B.
例1 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC的度数.
∵ ∠BEC是△AEC的一个外角,
∴ ∠BEC= ∠A+ ∠ACE,
∵∠A=42° ,∠ACE=18°,
∴ ∠BEC=60°.
∵ ∠BFC是△BEF的一个外角,
∴ ∠BFC= ∠ABD+ ∠BEF,
∵ ∠ABD=28° ,∠BEC=60°,
∴ ∠BFC=88°.
解:
F
A
C
D
E
B
利用三角形外角的性质求角的度数
例2 如图,P为△ABC内一点,∠BPC=150°, ∠ABP=20°,∠ACP=30°,求∠A的度数.
分析:延长BP交AC于E或连接AP并延长,构造三角形的外角,再利用外角的性质即可求出∠A的度数.
E
借助辅助线求角的度数
解:延长BP交AC于点E,
则∠BPC,∠PEC分别为△PCE,△ABE的外角,
∴∠BPC=∠PEC+∠PCE,
∠PEC=∠ABE+∠A,
∴∠PEC=∠BPC-∠PCE
=150°-30°=120°.
∴∠A=∠PEC-∠ABE=120°-20°=100°.
方法点拨:求角的度数,常连接并延长或延长三角形的边长,通过构造三角形的外角,利用外角的性质解决.
【变式题】 (一题多解)如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
E
)
)
1
2
)
3
)
4
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法三:延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外
角,请问∠CAD,∠CBE,∠BCF之间的
大小关系?
∴∠CAD+∠CBE+∠BCF=
(∠2+∠3)+(∠1+∠3)+(∠1+∠2)=
2(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,
∴∠CAD+∠CBE+∠BCF=360°.
有其他解法吗?
知识点3 三角形的外角和定理
新知探究
A
B
E
F
C
D
1
2
3
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外
角,请问∠CAD,∠CBE,∠BCF之间的
大小关系?
知识点3 三角形的外角和定理
新知探究
A
B
E
F
C
D
1
2
3
方法二 解:∵∠CAD,∠CBE,∠BCF是△ABC
的外角,
∴∠CAD+∠1=180°,则∠CAD=180°-∠1,∠CBE+∠2=180°,则∠CBE=180°-∠2, ∠BCF+∠3=180°,则∠BCF=180°-∠3.
如图,在△ABC中,∠CAD,∠CBE,∠BCF分别是点A,点B,点C处的一个外
角,请问∠CAD,∠CBE,∠BCF之间的
大小关系?
知识点3 三角形的外角和定理
新知探究
A
B
E
F
C
D
1
2
3
∵∠1,∠2,∠3是△ABC的三个内角,∴∠1+∠2+∠3=180°.
∴∠CAD+∠CBE+∠BCF=(180°-∠1)+(180°-
∠2)+(180°-∠3)=540°-(∠1+∠2+∠3)=360°.
解法三:过A作AM平行于BC,
∠3= ∠4
B
C
1
2
3
4
A
∠2= ∠BAM,
所以 ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAM=360°
M
∠2+ ∠ 3= ∠ 4+∠BAM,
【思考】你能总结出三角形的外角和的数量关系吗?
D
E
F
新知探究
推论:三角形的三个外角和等于360°.
三角形的每一个顶点处各有两个外角,三角形的外角和不是指六个外角的总和,而是说在三角形的每一个顶点处取一个外角,三个不同顶点处的外角和叫做三角形的外角和.
数学语言表示:
如图所示,∠CAD+∠CBE+∠BCF=360°.
三角形的外角和定理
A
B
E
F
C
D
1
2
3
例5 试说出下列图形中∠1和∠2的度数.
解:(1)∠1=180°-80°-60°=40°,∠2=80°+60°=140°.
(2)∠1=180°-30°-40°=110°,∠2=30°+40°=70°.
(3)∠1=90°-40°=50°,∠2=50°+90°=140°.
60?
80?
1
2
(1)
A
B
C
30?
40?
1
2
(2)
A
B
C
40?
2
1
┌
(3)
A
B
C
跟踪训练
新知探究
1.判断下列观点是否正确.
(1)三角形的外角都是钝角. ( )
(2)三角形的外角大于任何一个内角. ( )
(3)三角形的外角等于它的两个内角的和. ( )
(4)三角形的外角和等于360°. ( )
解:(1)三角形的外角是锐角、钝角或者直角.
(2)三角形的外角大于任何一个不相邻内角.
(3)三角形的外角等于它的不相邻两个内角的和.
随堂练习
解:∵AD⊥BC,
∴∠ADC=∠ADB=90°.
∵∠ADC是△ABD的外角, ∴∠ADC=∠1+∠2=90°.
∵∠1=∠2,∴∠1=∠2=45°.
2.如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数.
B
A
D
C
2
1
┐
∵∠ADB是△ACD的外角,
∴∠ADB=∠DAC+∠C=90°.
∵∠C=65°,
∴∠DAC=90°-∠C=25°.
则∠BAC=∠1+∠DAC=70°.
2.如图,AD⊥BC,∠1=∠2,∠C=65°,求∠BAC的度数.
B
A
D
C
2
1
┐
3.如图,∠ACD是△ABC的外角,CE平分∠ACD,若∠A=60°,∠B=40°,则∠ECD等于( )
A.40° B.45° C.50° D.55°
解析:∵∠A=60°,∠B=40°,
∴∠ACD=∠A+∠B=100°.
∵CE平分∠ACD,
∴∠ECD=50°.
A
B
C
D
E
C
4.小明把一副含有45°、30°的直角三角板如图摆放,若∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
解析:∵∠α、∠β是三角形的外角,
∴∠α=∠1+∠D,∠β=∠2+∠F.
∵∠1=∠3,∠2=∠4,
∴∠α+∠β=∠1+∠D+∠2+
∠F =∠3+∠4+∠D+∠ =210°.
B
E
B
C
A
F
D
α
β
1
2
3
4
三角形的外角
定义
性质
三角形
外角和
三角形的外角和等于360°
角的一边必须是三角形的一边,另一边必须是三角形的另一边的延长线
三角形的一个外角等于与其不相邻的两个内角的和
课堂小结
1.[2021广东汕头潮阳区期中]如图,在△ABC中,将△ABC沿直线m翻折,点B落在点D的位置,若∠1-∠2=60°,则∠B的度数是 .?
【解析】 如图,∵将△ABC沿直线m翻折,点B落在点D的位置,∠D=∠B,由三角形外角的性质,得∠1=∠B+∠3,∠3=∠2+∠D,∴∠1=∠2+∠D+∠B=∠2+2∠B, ∴∠1-∠2=2∠B=60°,∴∠B=30°.
拓展提升
2.已知五角星如图所示,求∠A+∠B+∠C+∠D+∠E的度数.
分析:利用三角形内角和定理和三角形外角的性质,
将∠A,∠B,∠C,∠D,∠E转化在同一个三角形中.仔细观察五角星,并在五角星中构建出△BGD和△CFE.
C
A
B
E
F
G
D
拓展提升
解:∵在△BGD中,∠AGF是它的外角,
∴∠AGF=∠B+∠D.
∵在△CFE中,∠AFG是它的外角,
∴∠AFG=∠C+∠E.
∵在△AFG中,∠A、∠AFG、∠AGF是三个内角,
∴∠A+∠AFG+∠AGF=180°,
则∠A+∠B+∠C+∠D+∠E=180°.
C
A
B
E
F
G
D
3.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数.
【解析】 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=(∠A+∠H)+(∠B+∠C)+ (∠D+∠E)+(∠F+∠G)=∠1+∠2+∠3+∠4=360°.
4.如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E,求证∠BAC=∠B+2∠E.
B
A
C
D
E
分析:利用角平分线的性质可以得出2倍
的数量关系的角.利用三角形外角性质,
将外角转化为两个不相邻内角的和.
将2倍数量关系的角和外角进行等量转化,即可得出
题目所要证明的结果.
证明:∵∠ECD是△EBC的外角,
∴∠ECD=∠B+∠E.
∵∠BAC是△ACE的外角,
∴∠BAC=∠E+∠ACE.
∵CE是∠ACD的角平分线,
∴∠ACE=∠ECD=∠B+∠E.
∴∠BAC=∠E+∠ACE=∠E+∠B+∠E=∠B+2∠E.
B
A
C
D
E
