12.2 三角形全等的判定(1)人教版初中数学八年级上册(共26张ppt)
文档属性
| 名称 | 12.2 三角形全等的判定(1)人教版初中数学八年级上册(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 858.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 11:02:13 | ||
图片预览



文档简介
(共26张PPT)
能够完全重合的两个三角形叫全等三角形。
2、
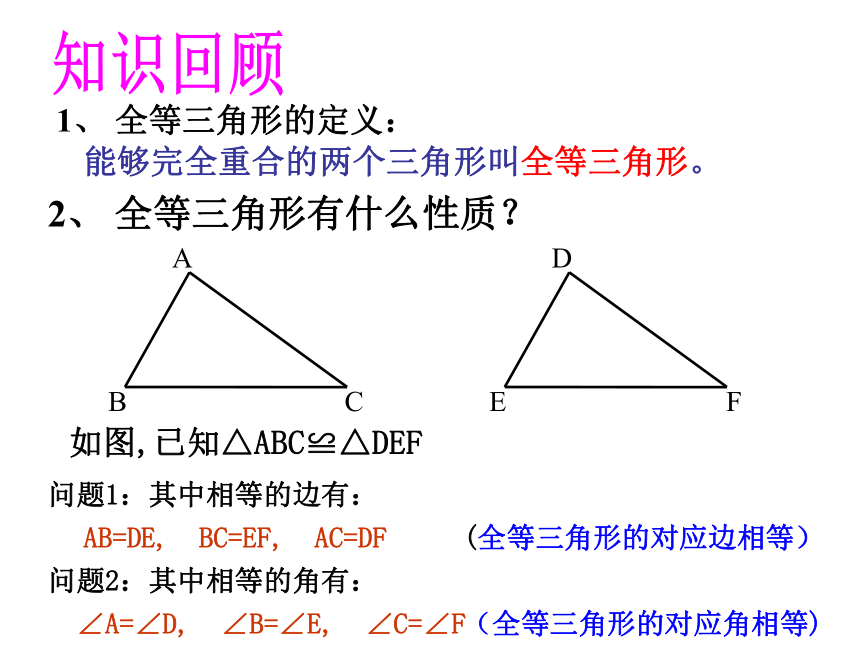
全等三角形有什么性质?
问题1:其中相等的边有:
问题2:其中相等的角有:
AB=DE,
BC=EF,
AC=DF
∠A=∠D,
∠B=∠E,
∠C=∠F
如图,已知△ABC≌△DEF
A
B
C
D
E
F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
1、
全等三角形的定义:
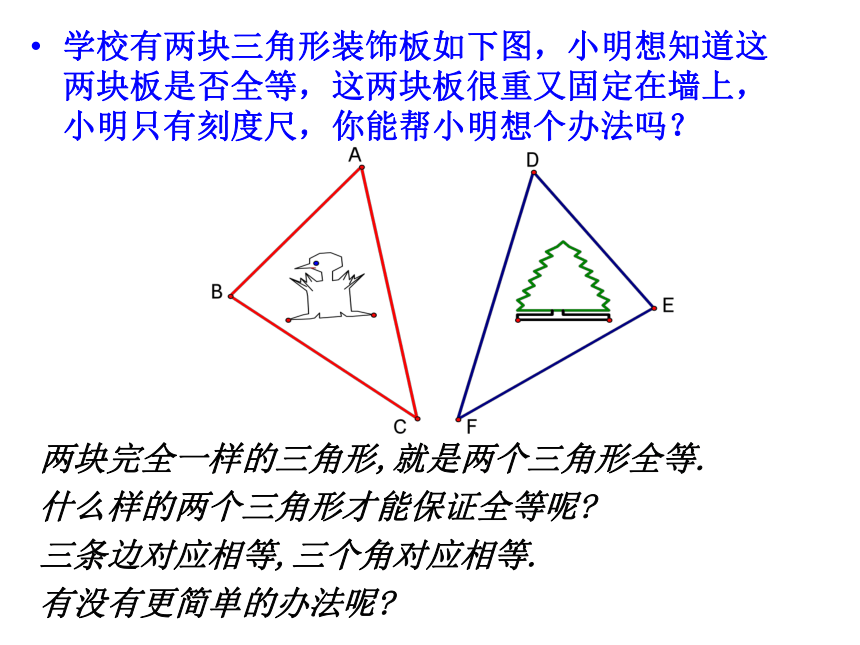
两块完全一样的三角形,就是两个三角形全等.
什么样的两个三角形才能保证全等呢?
三条边对应相等,三个角对应相等.
有没有更简单的办法呢?
学校有两块三角形装饰板如下图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?
先任意画出一个△ABC,再画一个△A/B/C/,使△ABC与△A/B/C/满足上述六个条件中的一个或两个.
你画出的△A/B/C/与△ABC一定全等吗?
探究1
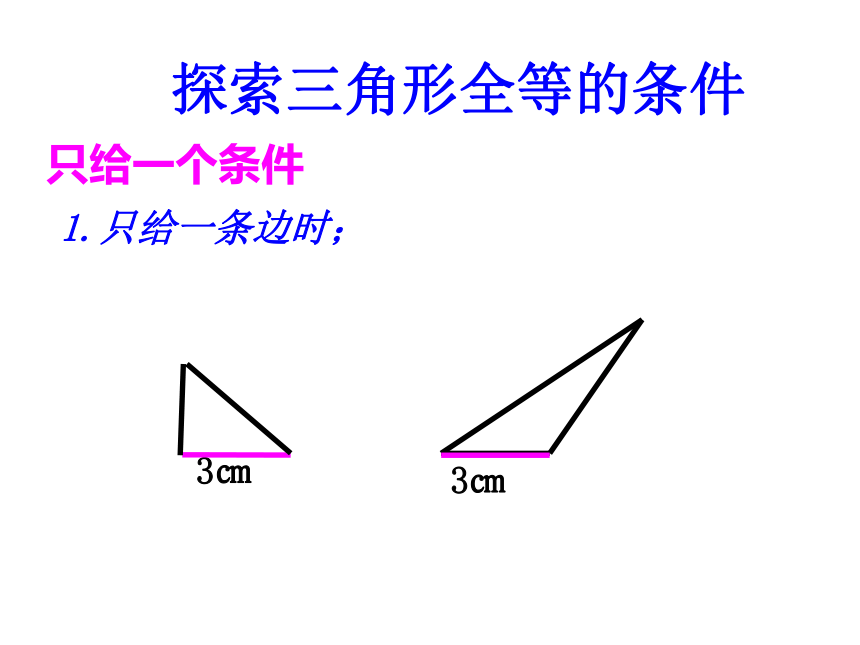
探索三角形全等的条件
1.只给一条边时;
3㎝
3㎝
只给一个条件
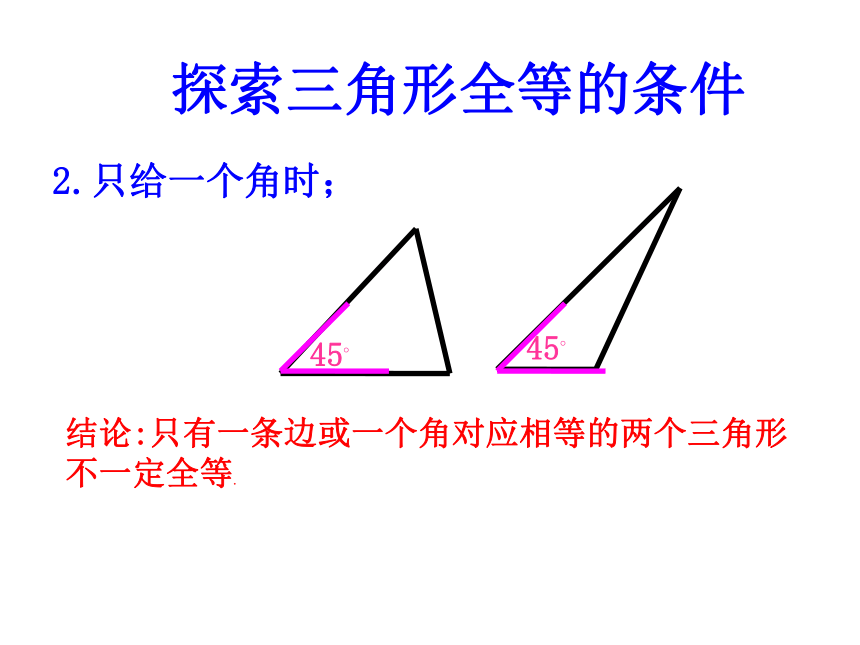
探索三角形全等的条件
45?
2.只给一个角时;
45?
结论:只有一条边或一个角对应相等的两个三角形
不一定全等.
如果给出两个条件画三角形,
你能说出有哪几种可能的情况?
①两角;
③一边一角。
②两边;
50?
30?
50?
30?
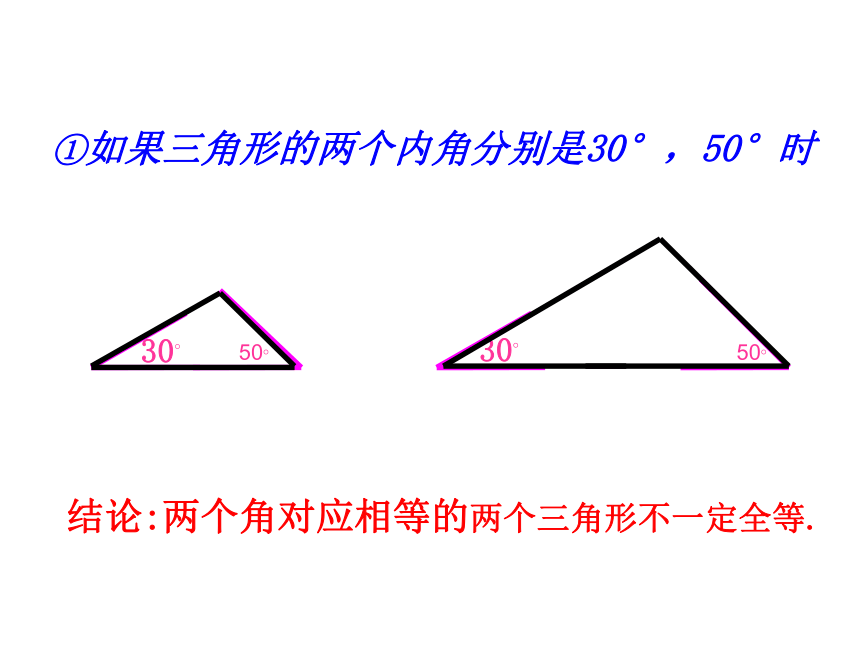
①如果三角形的两个内角分别是30°,50°时
结论:两个角对应相等的两个三角形不一定全等.
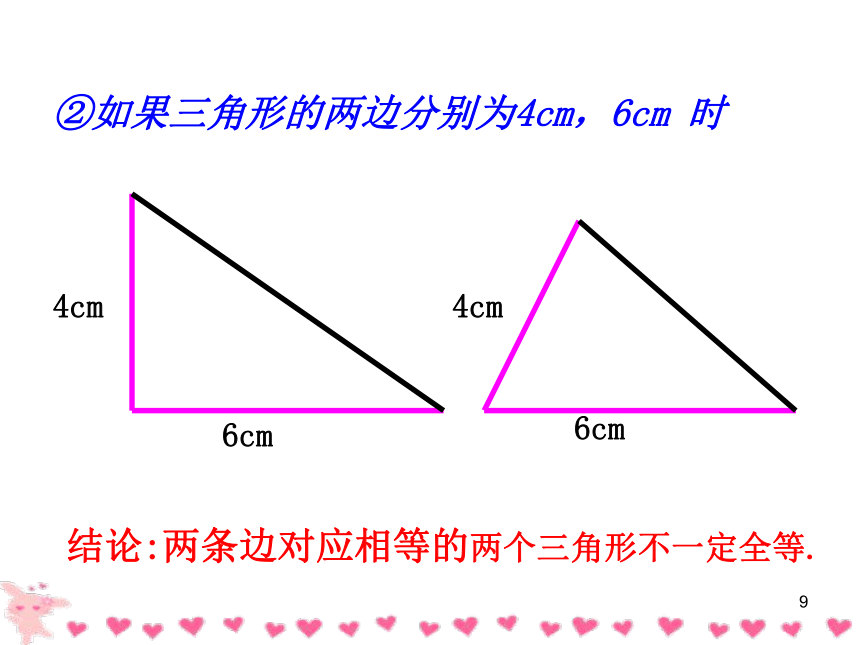
②如果三角形的两边分别为4cm,6cm
时
6cm
6cm
4cm
4cm
结论:两条边对应相等的两个三角形不一定全等.
③三角形的一个内角为30°,一条边为3cm时
3cm
3cm
30?
30?
结论:一条边一个角对应相等的两个三角形不一定全等.
两个条件
①两角;
②两边;
③一边一角。
结论:只给出一个或两个条件时,都不能保证所画的两个三角形一定全等。
一个条件
①一角;
②一边;
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三角;
②三边;
③两边一角;
④两角一边。
三个角:
300
700
800
300
700
800
如30°,70°,80°,它们
一定全等吗?
结论:三个角对应相等的两个三角形不一定全等.
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,
B/C/
=BC,A/C/
=AC.
把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
探究2
已知:任意
△
ABC,画一个△
A’B’C’,使A’B’=AB,A’C’=AC,B’C’=BC
画法:
1.
画线段B’C’=BC.
2.
分别以B’、C’为圆心,BA、CA为半径画弧,两弧相交于点A’.
3.
连结A’B’、A’C’.
△
A’B’C’就是所要画的三角形.
A
B
C
A’
B’
C’
问:通过实验可以发现什么事实?
画法
探究2反映的规律是:
三条边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
三角形的三边长度固定,这个三角形的形状大小就完全确定,这个性质叫三角形的稳定性.
小结:用上面的结论可以判断两个三角形全等.判断两个三角形全等的推理过程,叫做证明三角形全等.
规律
如何用符号语言来表达呢?
在△ABC与△DEF中,
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
利用尺规,作一个角等于
已知角.
已知:∠AOB(如图).
求作:∠AˊOˊBˊ,使
∠
AˊOˊBˊ=∠AOB.
B
O
A
交流提纲:
⑴你是怎样思考的;
⑵讨论:按怎么样的顺序画比较方便;
⑶画角时特别应注意什么?
作法与示范
作法
示范
(1)作射线O′A′:
(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′
A′于点C′;
(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D
′
;
(5)过点D
′作射线O
′
B
′
.
?
画一画?
A
C
B
D
分析:要证明两个三角形全等,需要那些条件?
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
例1
如图,
△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:
△ABD≌△ACD
若要求证:∠B=∠C,你会吗?
巩固练习
P37练习1.2
解:
△ABC≌△DCB
理由如下:
在△ABC和△DCB中
AB
=
CD
AC
=
DB
=
∴△ABC
≌
(
)
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
BC
△DCB
CB
SSS
A
B
C
D
再加把劲儿!!
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD
,
还需要条件
A
E
B
D
F
C
BF=CD
或
BD=CF
工人师傅常用角尺平分一个任意角,
做法
如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
即
OC
是∠AOB的平分线
OM=
ON,
OC=OC,
CM=CN,
∴
△OMC≌
△ONC
(SSS).
∴
∠MOC=∠NOC
(全等三角形的对应角相等)
证明:在
△OMC和△
ONC中,
小结:欲证角相等,转化为证三角形全等。
通过这节课的学习活动你有哪些收获?
课堂小结
(1)准备条件:证全等时要用的间接条件要先证好;
(2)证明三角形全等书写三步骤:
①写出在哪两个三角形中
②摆出三个条件用大括号括起来
③写出全等结论
3.证明三角形全等的步骤:
1.
边边边:三边对应相等的两个三角形全等(SSS)
2.三角形的稳定性及其应用
作
业:卷子1——5题
选做题:卷子6、7题
能够完全重合的两个三角形叫全等三角形。
2、
全等三角形有什么性质?
问题1:其中相等的边有:
问题2:其中相等的角有:
AB=DE,
BC=EF,
AC=DF
∠A=∠D,
∠B=∠E,
∠C=∠F
如图,已知△ABC≌△DEF
A
B
C
D
E
F
(全等三角形的对应边相等)
(全等三角形的对应角相等)
1、
全等三角形的定义:
两块完全一样的三角形,就是两个三角形全等.
什么样的两个三角形才能保证全等呢?
三条边对应相等,三个角对应相等.
有没有更简单的办法呢?
学校有两块三角形装饰板如下图,小明想知道这两块板是否全等,这两块板很重又固定在墙上,小明只有刻度尺,你能帮小明想个办法吗?
先任意画出一个△ABC,再画一个△A/B/C/,使△ABC与△A/B/C/满足上述六个条件中的一个或两个.
你画出的△A/B/C/与△ABC一定全等吗?
探究1
探索三角形全等的条件
1.只给一条边时;
3㎝
3㎝
只给一个条件
探索三角形全等的条件
45?
2.只给一个角时;
45?
结论:只有一条边或一个角对应相等的两个三角形
不一定全等.
如果给出两个条件画三角形,
你能说出有哪几种可能的情况?
①两角;
③一边一角。
②两边;
50?
30?
50?
30?
①如果三角形的两个内角分别是30°,50°时
结论:两个角对应相等的两个三角形不一定全等.
②如果三角形的两边分别为4cm,6cm
时
6cm
6cm
4cm
4cm
结论:两条边对应相等的两个三角形不一定全等.
③三角形的一个内角为30°,一条边为3cm时
3cm
3cm
30?
30?
结论:一条边一个角对应相等的两个三角形不一定全等.
两个条件
①两角;
②两边;
③一边一角。
结论:只给出一个或两个条件时,都不能保证所画的两个三角形一定全等。
一个条件
①一角;
②一边;
如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三角;
②三边;
③两边一角;
④两角一边。
三个角:
300
700
800
300
700
800
如30°,70°,80°,它们
一定全等吗?
结论:三个角对应相等的两个三角形不一定全等.
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB,
B/C/
=BC,A/C/
=AC.
把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
探究2
已知:任意
△
ABC,画一个△
A’B’C’,使A’B’=AB,A’C’=AC,B’C’=BC
画法:
1.
画线段B’C’=BC.
2.
分别以B’、C’为圆心,BA、CA为半径画弧,两弧相交于点A’.
3.
连结A’B’、A’C’.
△
A’B’C’就是所要画的三角形.
A
B
C
A’
B’
C’
问:通过实验可以发现什么事实?
画法
探究2反映的规律是:
三条边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
三角形的三边长度固定,这个三角形的形状大小就完全确定,这个性质叫三角形的稳定性.
小结:用上面的结论可以判断两个三角形全等.判断两个三角形全等的推理过程,叫做证明三角形全等.
规律
如何用符号语言来表达呢?
在△ABC与△DEF中,
A
B
C
D
E
F
AB=DE
AC=DF
BC=EF
∴△ABC≌△DEF(SSS)
利用尺规,作一个角等于
已知角.
已知:∠AOB(如图).
求作:∠AˊOˊBˊ,使
∠
AˊOˊBˊ=∠AOB.
B
O
A
交流提纲:
⑴你是怎样思考的;
⑵讨论:按怎么样的顺序画比较方便;
⑶画角时特别应注意什么?
作法与示范
作法
示范
(1)作射线O′A′:
(2)以点O为圆心,以OC长为半径画弧,交OA于点C,交OB于点D;
(3)以点O′为圆心,以OC长为半径画弧,交O′
A′于点C′;
(4)以点C′为圆心,以CD长为半径画弧,交前面的弧于点D
′
;
(5)过点D
′作射线O
′
B
′
.
?
画一画?
A
C
B
D
分析:要证明两个三角形全等,需要那些条件?
证明:∵D是BC的中点
∴BD=CD
在△ABD与△ACD中
AB=AC(已知)
BD=CD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
例1
如图,
△ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证:
△ABD≌△ACD
若要求证:∠B=∠C,你会吗?
巩固练习
P37练习1.2
解:
△ABC≌△DCB
理由如下:
在△ABC和△DCB中
AB
=
CD
AC
=
DB
=
∴△ABC
≌
(
)
1、如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。
BC
△DCB
CB
SSS
A
B
C
D
再加把劲儿!!
2、如图,D、F是线段BC上的两点,
AB=EC,AF=ED,要使△ABF≌△ECD
,
还需要条件
A
E
B
D
F
C
BF=CD
或
BD=CF
工人师傅常用角尺平分一个任意角,
做法
如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M、N重合,过角尺顶点C的射线OC便是∠AOB的平分线。为什么?
即
OC
是∠AOB的平分线
OM=
ON,
OC=OC,
CM=CN,
∴
△OMC≌
△ONC
(SSS).
∴
∠MOC=∠NOC
(全等三角形的对应角相等)
证明:在
△OMC和△
ONC中,
小结:欲证角相等,转化为证三角形全等。
通过这节课的学习活动你有哪些收获?
课堂小结
(1)准备条件:证全等时要用的间接条件要先证好;
(2)证明三角形全等书写三步骤:
①写出在哪两个三角形中
②摆出三个条件用大括号括起来
③写出全等结论
3.证明三角形全等的步骤:
1.
边边边:三边对应相等的两个三角形全等(SSS)
2.三角形的稳定性及其应用
作
业:卷子1——5题
选做题:卷子6、7题
