辽宁省盘锦市第二高级中学2012届高三第一次模拟考试数学(文)试题
文档属性
| 名称 | 辽宁省盘锦市第二高级中学2012届高三第一次模拟考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 575.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-06 13:09:20 | ||
图片预览


文档简介
考试时间:120分钟 满分:150分
一、选择题(共12个,每小题5分,共60分)
1.已知,,,则( )
A. B. C. D.
2.如果复数为纯虚数,则实数的值( )
A.1或2 B.1 C.2 D.不存在
3.下列函数中,既是偶函数,又在上单调递减的函数是( )
A. B. C. D.
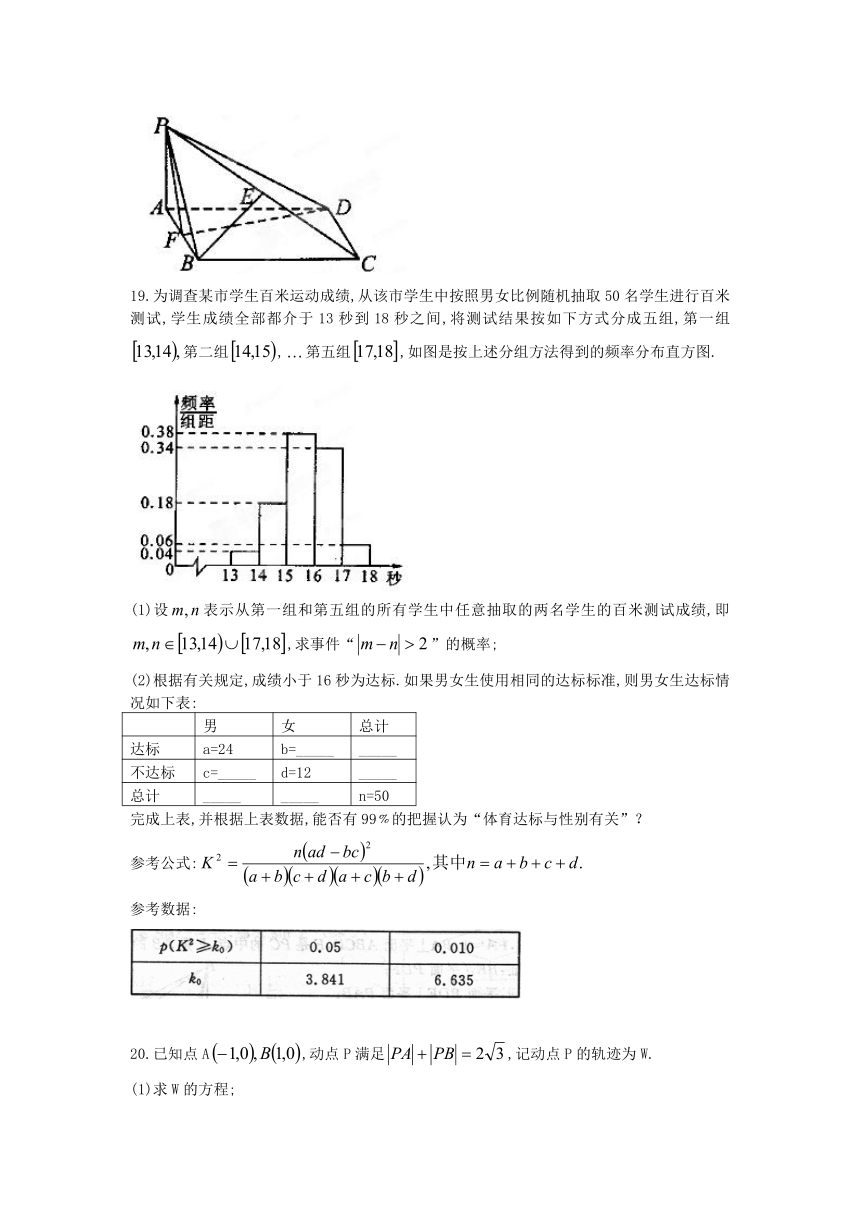
4.右侧框图中表示的程序所输出的结果是( )
A.1320 B.132 C.11880 D.121
5.设如果,那么( )
A. B. C. D.
6.4张卡片上分别写有数字1,2,3,4,从这四张卡片中随机抽取2张,则取出的2张卡片上数字之和为奇数的概率是( )
A. B. C. D.
7.一个四棱锥的三视图如图所示,其侧视图是等边三角形,该四棱锥的体积等于( )
A. B. C. D.
8.已知两个单位向量与的夹角为135,则>1的充要条件是( )
A. B. C. D.
9.函数的零点所在区间为( )
A. B. C. D.
10.过双曲线的焦点作圆的切线,切点为E延长交双曲线右支于点P,若E是的中点,则双曲线的离心率为( )
A. B. C. D.
11.先将函数的图象向左平移个单位,再保持所有点的纵坐标不变,横坐标压缩为原来的,得到函数的图象,则使为增函数的一个区间是( )
A. B. C. D.
12.给出下列四个命题:①,使得;②若是定义在的偶函数,且在上的增函数,,则;③△ABC,“A>”是“”的充要条件;④若函数的图象在点M处的切线方程是,则.其中所有正确命题的序号是( )
A.①② B.②③ C.③④ D.①④
二、填空题(每小题5分,共20分)
13.设则=_________
14.已知满足条件则的取值范围_________
15.在△ABC中,角A,B,C所对的边分别是,若,且,_________
16.已知过球面上A,B,C三点的截面和球心的距离是球直径的,且AB=3,AC⊥BC,则球面的面积为_________
三:简答题
17.已知数列满足,数列的前项和为,且,,求(1)数列的通项公式;
(2)令数列满足,求数列的前项和.
18.如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(1)求证:BE∥平面PDF;(2)求证:平面PDF⊥平面PAB;
(3)求三棱锥P-DEF的体积.
为调查某市学生百米运动成绩,从该市学生中按照男女比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组第二组,第五组,如图是按上述分组方法得到的频率分布直方图.
(1)设表示从第一组和第五组的所有学生中任意抽取的两名学生的百米测试成绩,即,求事件“”的概率;
(2)根据有关规定,成绩小于16秒为达标.如果男女生使用相同的达标标准,则男女生达标情况如下表:
男 女 总计
达标 a=24 b=_____ _____
不达标 c=_____ d=12 _____
总计 _____ _____ n=50
完成上表,并根据上表数据,能否有99﹪的把握认为“体育达标与性别有关”?
参考公式:
参考数据:
20.已知点A,动点P满足,记动点P的轨迹为W.
(1)求W的方程;
(2)直线与曲线W交于不同的两点C,D,若存在点M,使得成立,求实数的取值范围.
21. 已知函数
(1)若函数在定义域内单调递增,求的取值范围;
(2)若且关于的方程在上恰有两个不相等的实数根,求实数的取值范围.
四、选考题:(本小题满分10分)
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4-1:平面几何
如图,△ABC是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:△ABE≌△ACD;
(2)若AB=6,BC=4,求AE.
23.选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点,轴的正半轴为极轴,已知点P的直角坐标为,点M的极坐标为,若直线过点P,且倾斜角为,圆C以M为圆心、4为半径.
求直线的参数方程和圆C的极坐标方程;
试判定直线和圆C的位置关系.
24. 选修4-5:不等式
已知函数
解关于的不等式;
若函数的图象恒在函数图象的上方,求的取值范围.
盘锦市二高中高三第一次模拟答案 数学(文)
(2)
…+…………①
18.⑴证明:取PD中点为M,连EM、FM
因为E是PC中点 所以EM∥CD 且EM=CD
⑶V=
19.解: ⑴第一组有0.04×50=2名学生, 第五组有0.06×50=3名学生.
第一组2名学生记为1、2;第五组3名学生记为3、4、5.
=共10种记事件为A
男 女 总计
达标 a=24 b=6 30
不达标 c=8 d=12 20
总计 32 18 n=50
A= 所以P(A)=
⑵K 有99﹪的把握认为“体育达标与性别有关”
得 由韦达定理得
设CD中点为P则P
因为 所以点M在直线的垂直平分线上
因为直线的垂直平分线方程为
1 所以
2当
所以 即
⑵因为方程在上恰有两个不相等的实数根
即在上恰有两个不相等的实数根
设
令 得
所以在 且
所以
22.解:(Ⅰ)在△ABE和△ACD中,
∵AB=AC ∠ABE=∠ACD
23. (Ⅰ)直线的参数方程是为参数,圆C的极坐标方程是
(Ⅱ) 函数的图象恒在函数图象的上方,即对任意实数恒成立. 即对任意实数恒成立.
由于 所以的取值范围是.
一、选择题(共12个,每小题5分,共60分)
1.已知,,,则( )
A. B. C. D.
2.如果复数为纯虚数,则实数的值( )
A.1或2 B.1 C.2 D.不存在
3.下列函数中,既是偶函数,又在上单调递减的函数是( )
A. B. C. D.
4.右侧框图中表示的程序所输出的结果是( )
A.1320 B.132 C.11880 D.121
5.设如果,那么( )
A. B. C. D.
6.4张卡片上分别写有数字1,2,3,4,从这四张卡片中随机抽取2张,则取出的2张卡片上数字之和为奇数的概率是( )
A. B. C. D.
7.一个四棱锥的三视图如图所示,其侧视图是等边三角形,该四棱锥的体积等于( )
A. B. C. D.
8.已知两个单位向量与的夹角为135,则>1的充要条件是( )
A. B. C. D.
9.函数的零点所在区间为( )
A. B. C. D.
10.过双曲线的焦点作圆的切线,切点为E延长交双曲线右支于点P,若E是的中点,则双曲线的离心率为( )
A. B. C. D.
11.先将函数的图象向左平移个单位,再保持所有点的纵坐标不变,横坐标压缩为原来的,得到函数的图象,则使为增函数的一个区间是( )
A. B. C. D.
12.给出下列四个命题:①,使得;②若是定义在的偶函数,且在上的增函数,,则;③△ABC,“A>”是“”的充要条件;④若函数的图象在点M处的切线方程是,则.其中所有正确命题的序号是( )
A.①② B.②③ C.③④ D.①④
二、填空题(每小题5分,共20分)
13.设则=_________
14.已知满足条件则的取值范围_________
15.在△ABC中,角A,B,C所对的边分别是,若,且,_________
16.已知过球面上A,B,C三点的截面和球心的距离是球直径的,且AB=3,AC⊥BC,则球面的面积为_________
三:简答题
17.已知数列满足,数列的前项和为,且,,求(1)数列的通项公式;
(2)令数列满足,求数列的前项和.
18.如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
(1)求证:BE∥平面PDF;(2)求证:平面PDF⊥平面PAB;
(3)求三棱锥P-DEF的体积.
为调查某市学生百米运动成绩,从该市学生中按照男女比例随机抽取50名学生进行百米测试,学生成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组第二组,第五组,如图是按上述分组方法得到的频率分布直方图.
(1)设表示从第一组和第五组的所有学生中任意抽取的两名学生的百米测试成绩,即,求事件“”的概率;
(2)根据有关规定,成绩小于16秒为达标.如果男女生使用相同的达标标准,则男女生达标情况如下表:
男 女 总计
达标 a=24 b=_____ _____
不达标 c=_____ d=12 _____
总计 _____ _____ n=50
完成上表,并根据上表数据,能否有99﹪的把握认为“体育达标与性别有关”?
参考公式:
参考数据:
20.已知点A,动点P满足,记动点P的轨迹为W.
(1)求W的方程;
(2)直线与曲线W交于不同的两点C,D,若存在点M,使得成立,求实数的取值范围.
21. 已知函数
(1)若函数在定义域内单调递增,求的取值范围;
(2)若且关于的方程在上恰有两个不相等的实数根,求实数的取值范围.
四、选考题:(本小题满分10分)
请考生在第22、23、24三题中任选一题做答,如果多做,则按所做的第一题记分.
22.选修4-1:平面几何
如图,△ABC是内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.
(1)求证:△ABE≌△ACD;
(2)若AB=6,BC=4,求AE.
23.选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点,轴的正半轴为极轴,已知点P的直角坐标为,点M的极坐标为,若直线过点P,且倾斜角为,圆C以M为圆心、4为半径.
求直线的参数方程和圆C的极坐标方程;
试判定直线和圆C的位置关系.
24. 选修4-5:不等式
已知函数
解关于的不等式;
若函数的图象恒在函数图象的上方,求的取值范围.
盘锦市二高中高三第一次模拟答案 数学(文)
(2)
…+…………①
18.⑴证明:取PD中点为M,连EM、FM
因为E是PC中点 所以EM∥CD 且EM=CD
⑶V=
19.解: ⑴第一组有0.04×50=2名学生, 第五组有0.06×50=3名学生.
第一组2名学生记为1、2;第五组3名学生记为3、4、5.
=共10种记事件为A
男 女 总计
达标 a=24 b=6 30
不达标 c=8 d=12 20
总计 32 18 n=50
A= 所以P(A)=
⑵K 有99﹪的把握认为“体育达标与性别有关”
得 由韦达定理得
设CD中点为P则P
因为 所以点M在直线的垂直平分线上
因为直线的垂直平分线方程为
1 所以
2当
所以 即
⑵因为方程在上恰有两个不相等的实数根
即在上恰有两个不相等的实数根
设
令 得
所以在 且
所以
22.解:(Ⅰ)在△ABE和△ACD中,
∵AB=AC ∠ABE=∠ACD
23. (Ⅰ)直线的参数方程是为参数,圆C的极坐标方程是
(Ⅱ) 函数的图象恒在函数图象的上方,即对任意实数恒成立. 即对任意实数恒成立.
由于 所以的取值范围是.
同课章节目录
