2021—2022学年人教版数学七年级上册1.5.2 科学计数法与近似数 (共27张ppt)
文档属性
| 名称 | 2021—2022学年人教版数学七年级上册1.5.2 科学计数法与近似数 (共27张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 11:29:58 | ||
图片预览







文档简介
科学记数法与近似数
1.5.2 科学记数法
世界人口约7 000 000 000人
约300 000 000 m/s
约696 000 km
观察10的乘方的特点:
102=10×10=100
?
103=10×10×10=1 000
?
104=10×10×10×10= 10 000
?
?
?
1.5.2 科学记数法
102=10×10=100
?
103=10×10×10=1 000
?
104=10×10×10×10= 10 000
?
10????= 10?0
?
观察10的乘方的特点:
?
?
1.5.2 科学记数法
n个0
102=10×10=100
?
103=10×10×10=1 000
?
104=10×10×10×10= 10 000
?
10????= 10?0
?
观察10的乘方的特点:
?
?
1.5.2 科学记数法
n个0
一般地,10的n次幂等于10?0(在1的后面有n个0)
?
可以利用10的乘方表示一些大的数.
0
0
567 000 000
例如:
1.5.2 科学记数法
567 000 000=5.67×____________
?
567 000 000=5.67×100 000 000
?
5.67
0
0
0
0
=5.67×108
?
书写简单
便于读数
读作:
5.67乘以10的8次方(幂)
移动8位
把一个大于10的数表示成????×10????(其中?????大于或等于1且小于10,????是正整数),使用的是科学记数法.
?
1.5.2 科学记数法
567 000 000=5.67×100 000 000
?
=5.67×108
?
????×10????
?
把一个大于10的数表示成????×10????(其中?????大于或等于1且小于10,????是正整数),使用的是科学记数法.
?
1.5.2 科学记数法
辨析
567 000 000=56.7×10 000 000
?
=56.7×107
?
567 000 000=0.567×1 000 000 000
?
=0.567×109
?
不是科学记数法
1.5.2 科学记数法
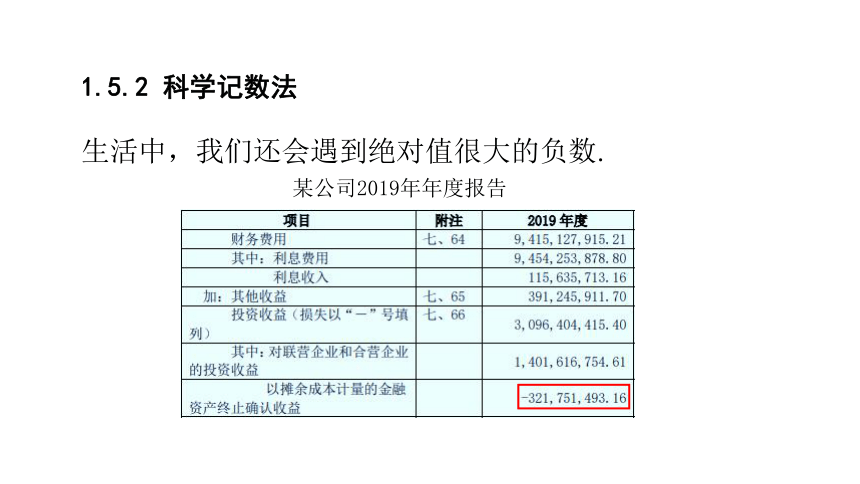
生活中,我们还会遇到绝对值很大的负数.
某公司2019年年度报告
1.5.2 科学记数法
像-567 000 000这样的负数,如何用科学记数法表示呢?
① 先写出它的相反数的科学记数法表示形式:
567 000 000=5.67×100 000 000
?
=5.67×108
?
② 再添加负号:
-567 000 000= -5.67×108
?
1.5.2 科学记数法
例1 用科学记数法表示下列各数:
1 000 000,57 000 000,-123 000 000 000.
解:
1 000 000
=1×1 000 000
?
????
?
????=6
?
=1×106
?
由10的乘方的特点得:
1 000 000
=106
?
????=1时,可以省略不写
?
×10 000 000
?
=5.7
1.5.2 科学记数法
例1 用科学记数法表示下列各数:
1 000 000,57 000 000,-123 000 000 000.
解:
????
?
????=7
?
57 000 000
=5.7×107
?
-123 000 000 000
=1.23×100 000 000 000
?
1.5.2 科学记数法
例1 用科学记数法表示下列各数:
1 000 000,57 000 000,-123 000 000 000.
解:
????
?
????=11
?
=1.23×1011
?
123 000 000 000
= -1.23×1011
?
123 000 000 000
57 000 000
1.5.2 科学记数法
用科学记数法????×10????表示一个大数时,如何能够快速、准确的找到????和????呢?
?
1 000 000
=1×106
?
=5.7×107
?
= 1.23×1011
?
.
.
.
左边数第一个数字后面点小数点,去掉最后一个不是0的数字后面的所有0,得到????.
?
=106
?
整数位 8位
57 000 000
1 000 000
123 000 000 000
1.5.2 科学记数法
用科学记数法????×10????表示一个大数时,如何能够快速、准确的找到????和????呢?
?
=1×106
?
=5.7×107
?
= 1.23×1011
?
整数位 7位
????=6
?
????=7
?
整数位 12位
????=11
?
=106
?
1.5.2 科学记数法
例2 下列用科学记数法表示的数,原来分别是什么数?
解:
1×105,2.03×107.
?
1×105
?
=100 000
2.03×107
?
=2.03×10 000 000
?
=20 300 000
可以利用10的指数与原数整数部分的位数之间的关系检验.
10的指数等于原数整数部分的位数减1.
1.5.2 科学记数法
小结
1.一个大数用科学记数法表示形式为????×10????(其中?????大于或等于1且小于10,????是正整数);
?
????的确定:左边数第一个数字后面点小数点,去掉最后一个不是0的数字后
面的所有0;
????的确定:原数的整数部分的位数减1.
?
1.5.2 科学记数法
小结
2.对于一个绝对值很大的负数,可以先把它的相反数用科学记数法表示出来,再添加负号.
另一个报道说:“约有五百人参加了今天的会议.”
一个报道说:“会议秘书处宣布,参加今天会议的有513人.”
1.5.3 近似数
准确数
近似数
许多情况下,很难取得准确数,或者不必使用准确数,而可以使用近似数. 比如,宇宙的年龄约为200亿年,长江长约为6 300 km,圆周率????约为3.14.
?
1.5.3 近似数
近似数与准确数的接近程度,可以用精确度表示.例如前面的五百是精确到百位的近似数,与准确数513的误差为13.
1.5.3 近似数
????≈3.142,精确到_____,或叫精确到_______
?
当我们用四舍五入法对圆周率????取近似数时,有
?
1.5.3 近似数
????≈3,精确到个位
?
????≈3.1,精确到0.1,或叫精确到十分位
?
????≈3.14,精确到0.01,或叫精确到百分位
?
0.001
千分位
????≈3.1416,精确到______,或叫精确到_______
?
0.000 1
万分位
1.5.3 近似数
例3 按括号内的要求,用四舍五入法对下列各数取近
似数.
(1)0.015 8(精确到0.001);
0.015 8≈0.016
解:
1.5.3 近似数
例3 按括号内的要求,用四舍五入法对下列各数取近
似数.
(2)304.35 (精确到个位);
304.35≈304
解:
1.5.3 近似数
例3 按括号内的要求,用四舍五入法对下列各数取近
似数.
(3)1.804 (精确到0.1);
1.804≈1.8
(4)1.804 (精确到0.01);
1.804≈1.80
这里的1.8和1.80的精确度相同吗?表示近似数时,能简单地把1.80后面的0去掉吗?
精确到百分位
精确到十分位
解:
1.5.3 近似数
小结
1.精确度的两种形式:
(1)精确到个位,十分位,百分位…;
(2)精确到1,0.1,0.01… .
2.近似数的表示方法:
先根据要求,找准所在位的数字,再把这个数字后面一位四舍五入.
谢 谢!
1.5.2 科学记数法
世界人口约7 000 000 000人
约300 000 000 m/s
约696 000 km
观察10的乘方的特点:
102=10×10=100
?
103=10×10×10=1 000
?
104=10×10×10×10= 10 000
?
?
?
1.5.2 科学记数法
102=10×10=100
?
103=10×10×10=1 000
?
104=10×10×10×10= 10 000
?
10????= 10?0
?
观察10的乘方的特点:
?
?
1.5.2 科学记数法
n个0
102=10×10=100
?
103=10×10×10=1 000
?
104=10×10×10×10= 10 000
?
10????= 10?0
?
观察10的乘方的特点:
?
?
1.5.2 科学记数法
n个0
一般地,10的n次幂等于10?0(在1的后面有n个0)
?
可以利用10的乘方表示一些大的数.
0
0
567 000 000
例如:
1.5.2 科学记数法
567 000 000=5.67×____________
?
567 000 000=5.67×100 000 000
?
5.67
0
0
0
0
=5.67×108
?
书写简单
便于读数
读作:
5.67乘以10的8次方(幂)
移动8位
把一个大于10的数表示成????×10????(其中?????大于或等于1且小于10,????是正整数),使用的是科学记数法.
?
1.5.2 科学记数法
567 000 000=5.67×100 000 000
?
=5.67×108
?
????×10????
?
把一个大于10的数表示成????×10????(其中?????大于或等于1且小于10,????是正整数),使用的是科学记数法.
?
1.5.2 科学记数法
辨析
567 000 000=56.7×10 000 000
?
=56.7×107
?
567 000 000=0.567×1 000 000 000
?
=0.567×109
?
不是科学记数法
1.5.2 科学记数法
生活中,我们还会遇到绝对值很大的负数.
某公司2019年年度报告
1.5.2 科学记数法
像-567 000 000这样的负数,如何用科学记数法表示呢?
① 先写出它的相反数的科学记数法表示形式:
567 000 000=5.67×100 000 000
?
=5.67×108
?
② 再添加负号:
-567 000 000= -5.67×108
?
1.5.2 科学记数法
例1 用科学记数法表示下列各数:
1 000 000,57 000 000,-123 000 000 000.
解:
1 000 000
=1×1 000 000
?
????
?
????=6
?
=1×106
?
由10的乘方的特点得:
1 000 000
=106
?
????=1时,可以省略不写
?
×10 000 000
?
=5.7
1.5.2 科学记数法
例1 用科学记数法表示下列各数:
1 000 000,57 000 000,-123 000 000 000.
解:
????
?
????=7
?
57 000 000
=5.7×107
?
-123 000 000 000
=1.23×100 000 000 000
?
1.5.2 科学记数法
例1 用科学记数法表示下列各数:
1 000 000,57 000 000,-123 000 000 000.
解:
????
?
????=11
?
=1.23×1011
?
123 000 000 000
= -1.23×1011
?
123 000 000 000
57 000 000
1.5.2 科学记数法
用科学记数法????×10????表示一个大数时,如何能够快速、准确的找到????和????呢?
?
1 000 000
=1×106
?
=5.7×107
?
= 1.23×1011
?
.
.
.
左边数第一个数字后面点小数点,去掉最后一个不是0的数字后面的所有0,得到????.
?
=106
?
整数位 8位
57 000 000
1 000 000
123 000 000 000
1.5.2 科学记数法
用科学记数法????×10????表示一个大数时,如何能够快速、准确的找到????和????呢?
?
=1×106
?
=5.7×107
?
= 1.23×1011
?
整数位 7位
????=6
?
????=7
?
整数位 12位
????=11
?
=106
?
1.5.2 科学记数法
例2 下列用科学记数法表示的数,原来分别是什么数?
解:
1×105,2.03×107.
?
1×105
?
=100 000
2.03×107
?
=2.03×10 000 000
?
=20 300 000
可以利用10的指数与原数整数部分的位数之间的关系检验.
10的指数等于原数整数部分的位数减1.
1.5.2 科学记数法
小结
1.一个大数用科学记数法表示形式为????×10????(其中?????大于或等于1且小于10,????是正整数);
?
????的确定:左边数第一个数字后面点小数点,去掉最后一个不是0的数字后
面的所有0;
????的确定:原数的整数部分的位数减1.
?
1.5.2 科学记数法
小结
2.对于一个绝对值很大的负数,可以先把它的相反数用科学记数法表示出来,再添加负号.
另一个报道说:“约有五百人参加了今天的会议.”
一个报道说:“会议秘书处宣布,参加今天会议的有513人.”
1.5.3 近似数
准确数
近似数
许多情况下,很难取得准确数,或者不必使用准确数,而可以使用近似数. 比如,宇宙的年龄约为200亿年,长江长约为6 300 km,圆周率????约为3.14.
?
1.5.3 近似数
近似数与准确数的接近程度,可以用精确度表示.例如前面的五百是精确到百位的近似数,与准确数513的误差为13.
1.5.3 近似数
????≈3.142,精确到_____,或叫精确到_______
?
当我们用四舍五入法对圆周率????取近似数时,有
?
1.5.3 近似数
????≈3,精确到个位
?
????≈3.1,精确到0.1,或叫精确到十分位
?
????≈3.14,精确到0.01,或叫精确到百分位
?
0.001
千分位
????≈3.1416,精确到______,或叫精确到_______
?
0.000 1
万分位
1.5.3 近似数
例3 按括号内的要求,用四舍五入法对下列各数取近
似数.
(1)0.015 8(精确到0.001);
0.015 8≈0.016
解:
1.5.3 近似数
例3 按括号内的要求,用四舍五入法对下列各数取近
似数.
(2)304.35 (精确到个位);
304.35≈304
解:
1.5.3 近似数
例3 按括号内的要求,用四舍五入法对下列各数取近
似数.
(3)1.804 (精确到0.1);
1.804≈1.8
(4)1.804 (精确到0.01);
1.804≈1.80
这里的1.8和1.80的精确度相同吗?表示近似数时,能简单地把1.80后面的0去掉吗?
精确到百分位
精确到十分位
解:
1.5.3 近似数
小结
1.精确度的两种形式:
(1)精确到个位,十分位,百分位…;
(2)精确到1,0.1,0.01… .
2.近似数的表示方法:
先根据要求,找准所在位的数字,再把这个数字后面一位四舍五入.
谢 谢!
