5.1.2-认识三角形（第2课时）

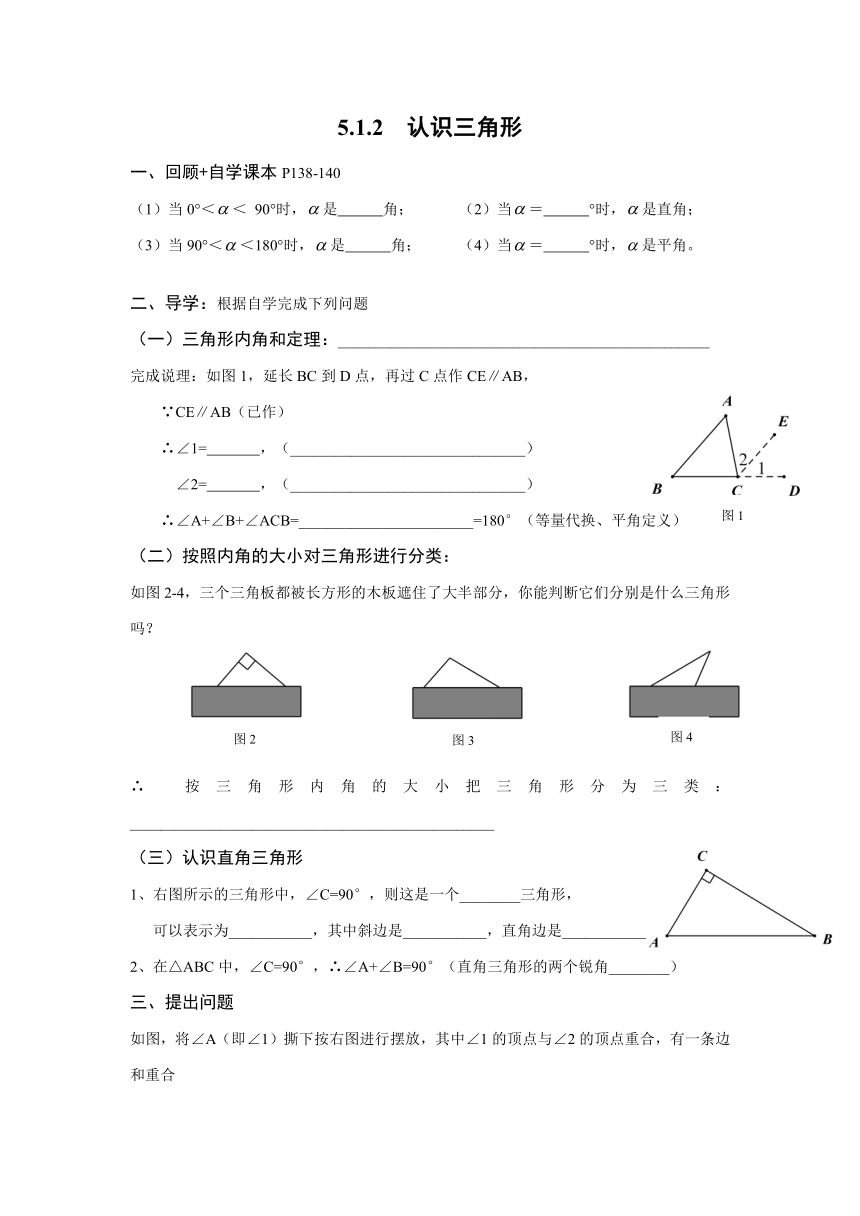
5.1.2 认识三角形
一、回顾+自学课本P138-140
（1）当0°＜＜ 90°时，是 角； （2）当＝ °时，是直角；
（3）当90°＜＜180°时，是 角； （4）当＝ °时，是平角。
二、导学：根据自学完成下列问题
（一）三角形内角和定理：_________________________________________________
完成说理：如图1，延长BC到D点，再过C点作CE∥AB，
∵CE∥AB（已作）
∴∠1= ，（_______________________________）
∠2= ，（_______________________________）
∴∠A+∠B+∠ACB=_______________________=180°（等量代换、平角定义）
（二）按照内角的大小对三角形进行分类：
如图2-4，三个三角板都被长方形的木板遮住了大半部分，你能判断它们分别是什么三角形吗？
∴ 按三角形内角的大小把三角形分为三类：________________________________________________
（三）认识直角三角形
1、右图所示的三角形中，∠C=90°，则这是一个________三角形，
可以表示为___________，其中斜边是___________，直角边是___________
2、在△ABC中，∠C=90°，∴∠A+∠B=90°（直角三角形的两个锐角________）
三、提出问题
如图，将∠A（即∠1）撕下按右图进行摆放，其中∠1的顶点与∠2的顶点重合，有一条边和重合
于是，∠A=∠1 ，∴a∥b（_______________________________）
∴ ∠3+∠BCD=180°（_______________________________）
即∠3+∠2+∠A=_________（等量代换）∴三角形的内角和为180°
四、初步应用
1、观察下边的三角形，把它们标入相应的空内；
锐角三角形：
直角三角形：
钝角三角形：
2、在△ABC中，
（1）∠C=30°，∠A=50°，这是一个 三角形；
（2）∠B=50°，∠A=∠C，则∠C= °，这是一个 三角形；
3、如右图，在△ABC中，∠A∶∠B∶∠C=3∶2∶1，求三个内角的度数。
五、小结:本节课你收获了什么 用自己的话整理下来
六、验收落实
1、在△ABC中，∠A=60°，∠C=80°，则∠B= 度；
在一个三角形的内角中，最多有 个钝角，至少有 个锐角。
3、在Rt△ABC中，已知∠C=90°，且∠A=2∠B，则B= ； 第4题图
4、如图，已知△ABC，将BC延长到点D，若∠ACD=135°，则∠A+∠B= °。
5、如图，已知∠ACB=90°，CD⊥AB，垂足是D
（1）图中有几个直角三角形，是哪几个 分别说出它们的直角边和斜边
（2）∠1和∠A什么关系 ∠2和∠2呢
6、（A层）如图：在△ABC中，∠A=50°，∠ABC=70°，BD⊥AC，求∠DBC的度数；
图1
图3
图4
图2