统计期末单元复习测试题B-2020-2021学年人教A版(2019)高中数学选择性必修第二册(Word版含解析)
文档属性
| 名称 | 统计期末单元复习测试题B-2020-2021学年人教A版(2019)高中数学选择性必修第二册(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 00:00:00 | ||
图片预览



文档简介
统计期末单元复习测试题B
一.选择题(共8小题)
1.某校有200位教职员工,其每周用于锻炼所用时间的频率分布直方图如图所示.据图估计,每周锻炼时间在,小时内的人数为
A.18 B.36 C.54 D.72
2.在发生某公共卫生事件期间、有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续14天,每天新增疑似病例不超过6人”.根据过去14天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A.甲地:总体均值为1,中位数为1
B.乙地:总体均值为1,总体标准差大于0
C.丙地:中位数为1,众数为2
D.丁地:总体均值为2,总体方差为1
3.某工厂利用随机数表对生产的50个零件进行抽样测试,先将50个零件进行编号,编号分别为01,02,,50,从中抽取5个样本,下面提供随机数表的第1行到第2行:
66 67 40 37 14 64 05 71 11 05 65 09 95 86 68 76 83 20 37 90
57 16 03 11 63 14 90 84 45 21 75 73 88 05 90 52 23 59 43 10
若从表中第1行第9列开始向右依次读取数据,则得到的第4个样本编号是
A.10 B.09 C.71 D.20
4.电影《你好,李焕英》于2021年2月12日在中国内地上映,创造了连续多日的单日票房冠军.某新闻机构想了解全国人民对《你好,李焕英》的评价,决定从某市3个区按人口数用分层抽样的方法抽取一个样本.若3个区人口数之比为,且人口最少的一个区抽出100人,则这个样本的容量等于
A.400 B.450 C.500 D.550
5.“新冠肺炎”席卷全球,我国医务工作者为了打好这次疫情阻击战,充分发挥优势,很快抑制了病毒,据统计老年患者治愈率为,中年患者治愈率为,青年患者治愈率为.如果某医院有30名老年患者,40名中年患者,50名青年患者,则估计该医院的平均治愈率是
A. B. C. D.
6.一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是
A.这组新数据的平均数为 B.这组新数据的平均数为
C.这组新数据的方差为 D.这组新数据的标准差为
7.江西省重点中学协作体于2020年进行了一次校际数学竞赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在,之间,其得分的频率分布直方图如图,则下列结论错误的是
A.得分在,之间的共有40人
B.从这100名参赛者中随机选取1人,其得分在,的概率为0.5
C.这100名参赛者得分的中位数为65
D.可求得
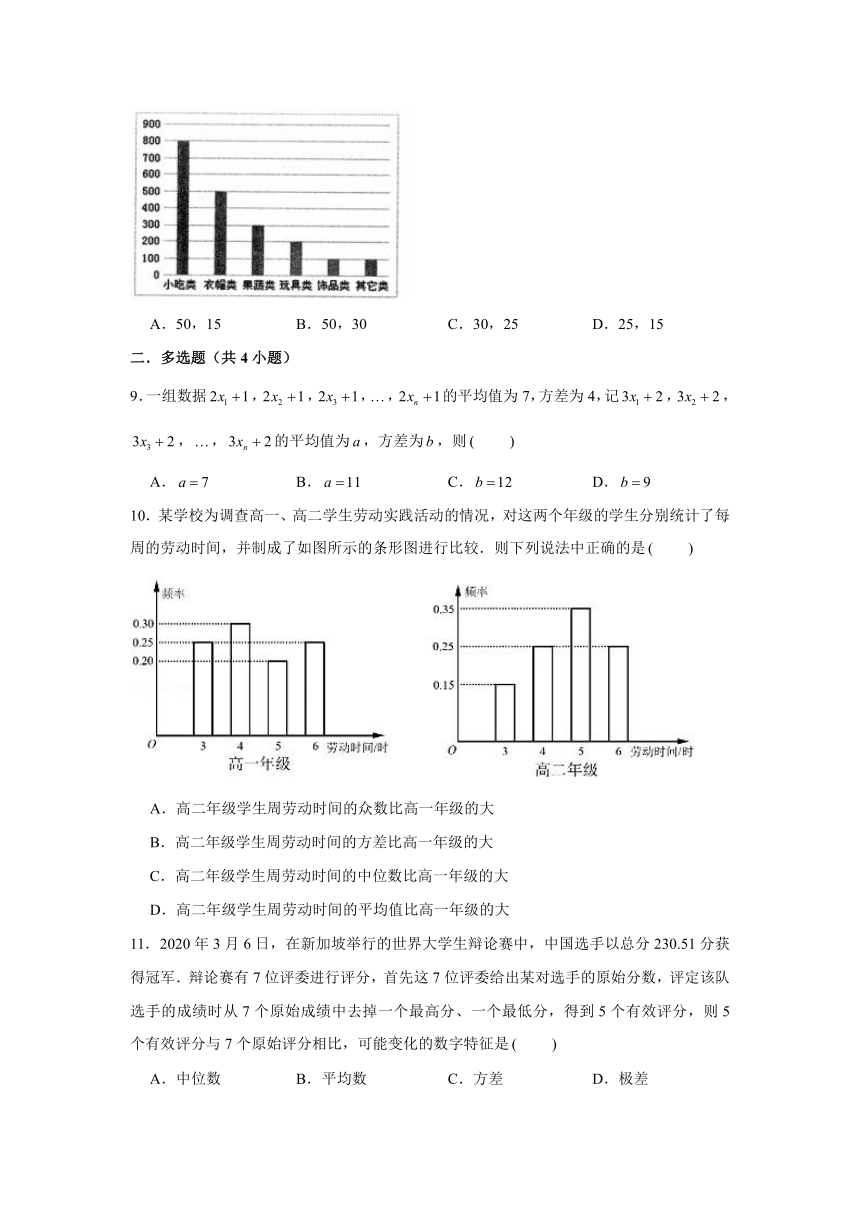
8.在文明城市创建过程中,某市创建办公室对市区内从事小吃、衣帽、果蔬、玩具等6类商户数进行了统计并绘成如图所示的条形统计图,对商户进行了文明城市知识教育培训.2021年初,该市创建办公室计划从2000户商户中,按照商户类型进行分层抽样,随机抽取100户进行文明城市知识教育培训效果调查,则衣帽类和果蔬类商户抽取的户数分别为
A.50,15 B.50,30 C.30,25 D.25,15
二.多选题(共4小题)
9.一组数据,,,,的平均值为7,方差为4,记,,,,的平均值为,方差为,则
A. B. C. D.
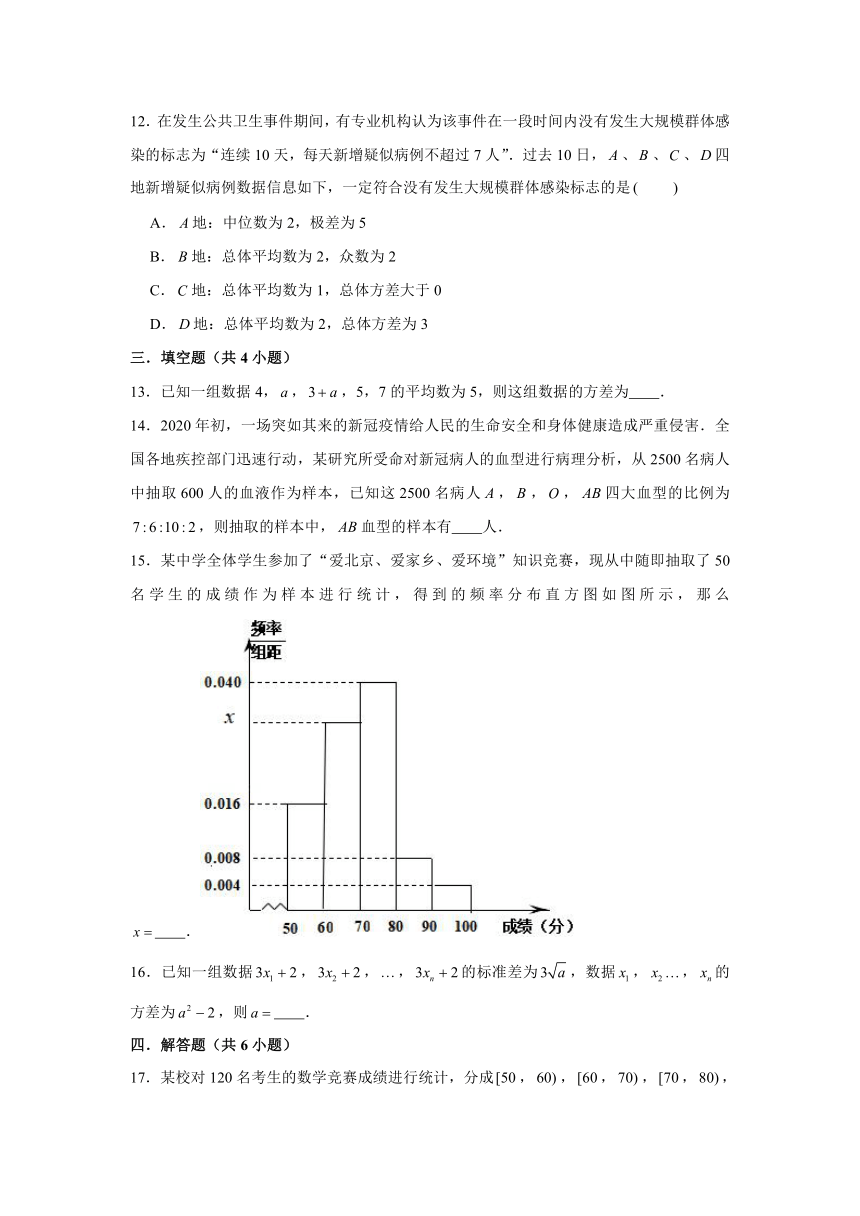
10.某学校为调查高一、高二学生劳动实践活动的情况,对这两个年级的学生分别统计了每周的劳动时间,并制成了如图所示的条形图进行比较.则下列说法中正确的是
A.高二年级学生周劳动时间的众数比高一年级的大
B.高二年级学生周劳动时间的方差比高一年级的大
C.高二年级学生周劳动时间的中位数比高一年级的大
D.高二年级学生周劳动时间的平均值比高一年级的大
11.2020年3月6日,在新加坡举行的世界大学生辩论赛中,中国选手以总分230.51分获得冠军.辩论赛有7位评委进行评分,首先这7位评委给出某对选手的原始分数,评定该队选手的成绩时从7个原始成绩中去掉一个最高分、一个最低分,得到5个有效评分,则5个有效评分与7个原始评分相比,可能变化的数字特征是
A.中位数 B.平均数 C.方差 D.极差
12.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,、、、四地新增疑似病例数据信息如下,一定符合没有发生大规模群体感染标志的是
A.地:中位数为2,极差为5
B.地:总体平均数为2,众数为2
C.地:总体平均数为1,总体方差大于0
D.地:总体平均数为2,总体方差为3
三.填空题(共4小题)
13.已知一组数据4,,,5,7的平均数为5,则这组数据的方差为 .
14.2020年初,一场突如其来的新冠疫情给人民的生命安全和身体健康造成严重侵害.全国各地疾控部门迅速行动,某研究所受命对新冠病人的血型进行病理分析,从2500名病人中抽取600人的血液作为样本,已知这2500名病人,,,四大血型的比例为,则抽取的样本中,血型的样本有 人.
15.某中学全体学生参加了“爱北京、爱家乡、爱环境”知识竞赛,现从中随即抽取了50名学生的成绩作为样本进行统计,得到的频率分布直方图如图所示,那么 .
16.已知一组数据,,,的标准差为,数据,,的方差为,则 .
四.解答题(共6小题)
17.某校对120名考生的数学竞赛成绩进行统计,分成,,,,,,,,,五组,得到如图所示频率分布直方图.
(1)求图中的值;
(2)估计该校学生数学竞赛成绩的平均数;
(3)估计该校学生数学竞赛成绩的第80百分位数落在哪一组.
18.2016年某省人社厅推出15项改革措施,包括机关事业单位基本养老保险制度改革、调整机关事业单位工资标准、全省县以下机关建立职务与职级并行制度.某市为了了解该市市民对这些改革措施的态度,在该市随机抽取了50名市民进行调查,作出了他们月收入(单位:百元,范围:,的频率分布直方图,同时得到其中各种月收入情况的市民对该项政策赞成的人数统计表.
月收入 赞成人数
, 4
, 8
, 12
, 5
, 2
, 2
(1)求月收入在百元内的频率,并补全这个频率分布直方图,在图中标出相应的纵坐标;
(2)根据频率分布直方图估计这50人的平均月收入;
(3)为了这个改革方案能够更好的实施,从这些调查者中选取代表提供建议,若从月收入在,百元和,百元的不赞成的被调查者中随机抽取2人,求这两名代表月收入差不超过1000元的概率.
19.高三年级计划从甲、乙两个班中选择一个班参加学校的知识竞赛,设甲班的成绩为,乙班的成绩为,两个班以往6次竞赛的成绩统计如表:
1 2 3 4 5 6
133 145 118 125 132 127
128 139 121 144 127 121
(1)请计算甲、乙两班的平均成绩和方差,从求得数据出发确定派哪个班参加竞赛更合适(方差保留一位小数);
(2)若,则称甲、乙属于“同一阶层”.若从上述6次考试中任取三次,求至少有两次甲、乙属于“同一阶层”的概率.
附:方差.
20.某社区组织了以“共同保护生态环境,共建绿色生态环境家园”为主题的垃圾分类、环境保护宣传咨询服务活动.组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组,,第2组,,第3组,,第4组,,第5组,,得到的频率分布直方图如图所示.
(1)若电视台记者要从抽取的群众中选1人进行采访,求被采访人恰好在第2组或第4组的概率;
(2)已知第1组群众中男性有2人,组织方要从第1组中随机抽取2名群众组成宣传志愿者服务小组,求至少有1名男性的概率.
21.为了更好地刺激经济复苏,增加就业岗位,多地政府出台支持“地摊经济”的举措.某市城管委对所在城市约6000个流动商贩进行调查统计,发现所售商品多为小吃、衣帽、玩具、饰品、果蔬等,各类商贩所占比例如图.
(1)该市城管委为了更好地服务百姓,打算从流动商贩中随机抽取100家进行政策问询.如果按照分层抽样的方式抽取,请问果蔬类、小吃类商贩各抽取多少家?
(2)为了更好的了解商贩的收入情况,工作人员对某果蔬商贩最近50天的日收入进行了统计(单位:元),所得频率分布直方图如图所示:
(ⅰ)请根据频率分布直方图估计该果蔬商贩的日平均收入(同一组中的数据用该组区间的中间值代替);
(ⅱ)若从该果蔬商贩这50天中日收入不低于250元的天数中随机抽取2天,求这2天的日收入至少有一天不低于300元的概率.
22.某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如图频率分布直方图,其中时间分组为,,,,,,,,,.
(Ⅰ)求频率分布直方图中的值;
(Ⅱ)从统计学的角度说明学校是否需要推迟5分钟上课;
(Ⅲ)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求这两个学生的单程时间均落在,上的概率.
统计期末单元复习测试题B
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由频率分布直方图得:
每周锻炼时间在,小时内的频率为:,
每周锻炼时间在,小时内的人数为:.
故选:.
2.【解答】解:选项,总体均值为1,中位数为1,可能存在某一天超过6人,
例如:前6天0人,天1人,第14天7人,故选项不正确;
选项,总体均值为1,总体标准差大于0,可能存在某一天超过6人,
例如:前13天0人,第14天14人,故选项不正确;
选项,中位数为1,众数为2,可能存在某一天超过6人,
例如:前4天0人,天1人,天2人,第14天8人,故选项不正确;
选项,总体均值为2,总体方差为1,设为当天病例数,,,,
,若,则一定大于1,所以.
故选项正确.
故选:.
3.【解答】解:从表中第1行第9列开始向右依次读取数据,找出4个在内的编号,14,05,11,09,20.
则得到的第4个样本编号09.
故选:.
4.【解答】解:从某市3个区按人口数用分层抽样的方法抽取一个样本.
3个区人口数之比为,且人口最少的一个区抽出100人,
设这个样本的容量为,
则,
解得.
这个样本的容量等于450.
故选:.
5.【解答】解:利用求加权平均数的公式解得:,
故选:.
6.【解答】解:根据题意,一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,
则新数据的平均数为,方差为,
则其标准差为,
故选:.
7.【解答】解:由频率分布直方图得:
对于,得分在,之间有:人,故正确;
对于,从这100名参赛者中随机选取1人,其得分在,的概率为:
,故正确;
对于,,解得,故正确;
对于,,的频率为,
,的频率为,
这100名参赛者得分的中位数为:,故错误.
故选:.
8.【解答】解:共有2000户,需要抽取100户,故抽取的比例为,
由统计图可知,衣帽类有500户,果蔬类有300户,
则衣帽类抽样户,果蔬类抽取户.
故选:.
二.多选题(共4小题)
9.【解答】解:,,,,的平均值为7,方差为4,
设,,,,,
,得,
,,
,,,,的平均值为,方差为,
,
,
故选:.
10.【解答】解:由条形统计图得:
对于,高一学生周劳动时间的众数为4,高二学生周劳动时间的众数为5,
高二年级学生周劳动时间的众数比高一年级的大,故正确;
对于,高一年级学生周劳动时间差异相对较大,高二年级的周劳动时间的差异较小,
高二年级学生周劳动时间的方差比高一年级的小,故错误;
对于,高一年级学生周劳动时间的中位数为4,高二年级学生周劳动时间的中位数为5,
高二年级学生周劳动时间的中位数比高一年级的大,故正确;
对于,高一年级学生周劳动时间的平均值为:(小时),
高二年级学生周劳动时间的平均值为:(小时),
高二年级学生周劳动时间的平均值比高一年级的大,故正确.
故选:.
11.【解答】解:因为7个有效评分是9个原始评分中去掉一个最高分、一个最低分,
所以中位数不变,平均数、方差、极差可能发生变化,
所以变化的数字特征是平均数、方差、极差,
故选:.
12.【解答】解:该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.
在地,中位数为2,极差为5,,每天新增疑似病例不会超过7人,所以地符合标准;
在地,总体平均数为2,众数为2,如0,0,0,0,2,2,2,2,2,10,每天新增疑似病例可以超过7人,所以地不符合标准;
在地,总体平均数为1,总体方差大于0,如,0,0,0,0,0,0,0,0,0,10,每天新增疑似病例可以超过7人,所以地不符合标准;
在地,总体平均数为2,总体方差为3.根据方差公式,如果存在大于7的数存在,
根据方差公式,若出现大于7的数值8,则,与总体方差为3矛盾,因而不会出现超过7人的情况,所以地符合标准.
故选:.
三.填空题(共4小题)
13.【解答】解:因为这组数据的平均数为5,
所以,解得,
则这组数为3,4,5,6,7,
故方差.
故答案为:2.
14.【解答】解:根据分层抽样原理知,抽取600人的样本中,
血型的样本数为(人.
故答案为:48.
15.【解答】解:,故.
16.【解答】解:数据,,,的标准差为,
所以数据,,的标准差是,
它的方差是,即,
解方程得或(舍去),
所以.
故答案为:2.
四.解答题(共6小题)
17.【解答】解:(1)由频率分布直方图得:
,
解得.
(2)估计该校学生数学竞赛成绩的平均数为:
.
(3),的频率为,
,的频率为,
估计该校学生数学竞赛成绩的第80百分位数落在,内.
18.【解答】解:(1)月收入在百元内的频率为
;
由,补全这个频率分布直方图,如图所示;
(2)由频率分布直方图,计算平均数为
(百元),
即这50人的平均月收入估计为4300元;
(3),内的人数为15人,其中12人赞成,3人不赞成;
记不赞成的人为,,,;
,内的人数为5人,其中2人赞成,3人不赞成;
记不赞成的3人为,,;
从不赞成的6人中任取2人,基本事件是:
,,,,,,,,,,,,,,共15种情况;
其中两代表月收入差不超过1000元的有,,,,,,共6种情况,
故这两代表月收入不超过1000元的概率是.
19.【解答】解:(1)计算甲班的平均成绩为,
方差为;
乙班的平均成绩为,
方差为;
由于,,所以派甲班参加比赛更合适.
(2)上述6次考试中有1,3,5的成绩为甲、乙属于“同一阶段;
从6次考试中任选三次,总共有:
,2,,,2,,,2,,,2,,,3,,
,3,,,3,,,4,,,4,,,5,,
,3,,,3,,,3,,,4,,,4,,
,5,,,4,,,4,,,5,,,5,共20种结果;
其中至少有两次甲、乙属于“同一阶段”的有:
,2,,,2,,,3,,,3,,,3,,
,4,,,5,,,3,,,4,,,5,共10次;
则至少有两次甲、乙属于“同一阶段”的概率为.
20.【解答】解:(1)第2组的频率为,
第4组的频率为,
所以被采访人恰好在第2组或第4组的概率为;
(2)第1组的频数为,其中男性有2人,女性有4人,
所以从中抽取两名群众,至少有一名男性的概率为.
21.【解答】解:(1)由扇形统计图可知,果蔬类商贩所占比例为,故果蔬类商贩抽取家,
小吃类商贩所占比例为,故小吃类商贩抽取家;
(2)估计该果蔬商贩的日平均收入为:元;
日收入不低于250元的天数为天,
日收入不低于300元的天数为天,
所以这2天的日收入至少有一天不低于300元的概率为.
22.【解答】解:(1)时间分组为,的频率为:
,
.
(2)100个非住校生上学路上单程所需时间的平均数为:
.
,该校不需要推迟5分钟上课.
(3)从单程所需时间不小于30分钟的5名学生中,随机抽取2人共有以下10种情况:
,,,,,,,,,,
,,,,,,,,,,
其中恰有一个学生的单程所需时间落在,中的有以下3种:,,,,,;
两个学生的单程时间均落在,上的概率为.
一.选择题(共8小题)
1.某校有200位教职员工,其每周用于锻炼所用时间的频率分布直方图如图所示.据图估计,每周锻炼时间在,小时内的人数为
A.18 B.36 C.54 D.72
2.在发生某公共卫生事件期间、有专业机构认为该事件在一段时间没有发生在规模群体感染的标志为“连续14天,每天新增疑似病例不超过6人”.根据过去14天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是
A.甲地:总体均值为1,中位数为1
B.乙地:总体均值为1,总体标准差大于0
C.丙地:中位数为1,众数为2
D.丁地:总体均值为2,总体方差为1
3.某工厂利用随机数表对生产的50个零件进行抽样测试,先将50个零件进行编号,编号分别为01,02,,50,从中抽取5个样本,下面提供随机数表的第1行到第2行:
66 67 40 37 14 64 05 71 11 05 65 09 95 86 68 76 83 20 37 90
57 16 03 11 63 14 90 84 45 21 75 73 88 05 90 52 23 59 43 10
若从表中第1行第9列开始向右依次读取数据,则得到的第4个样本编号是
A.10 B.09 C.71 D.20
4.电影《你好,李焕英》于2021年2月12日在中国内地上映,创造了连续多日的单日票房冠军.某新闻机构想了解全国人民对《你好,李焕英》的评价,决定从某市3个区按人口数用分层抽样的方法抽取一个样本.若3个区人口数之比为,且人口最少的一个区抽出100人,则这个样本的容量等于
A.400 B.450 C.500 D.550
5.“新冠肺炎”席卷全球,我国医务工作者为了打好这次疫情阻击战,充分发挥优势,很快抑制了病毒,据统计老年患者治愈率为,中年患者治愈率为,青年患者治愈率为.如果某医院有30名老年患者,40名中年患者,50名青年患者,则估计该医院的平均治愈率是
A. B. C. D.
6.一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,则下列说法正确的是
A.这组新数据的平均数为 B.这组新数据的平均数为
C.这组新数据的方差为 D.这组新数据的标准差为
7.江西省重点中学协作体于2020年进行了一次校际数学竞赛,共有100名同学参赛,经过评判,这100名参赛者的得分都在,之间,其得分的频率分布直方图如图,则下列结论错误的是
A.得分在,之间的共有40人
B.从这100名参赛者中随机选取1人,其得分在,的概率为0.5
C.这100名参赛者得分的中位数为65
D.可求得
8.在文明城市创建过程中,某市创建办公室对市区内从事小吃、衣帽、果蔬、玩具等6类商户数进行了统计并绘成如图所示的条形统计图,对商户进行了文明城市知识教育培训.2021年初,该市创建办公室计划从2000户商户中,按照商户类型进行分层抽样,随机抽取100户进行文明城市知识教育培训效果调查,则衣帽类和果蔬类商户抽取的户数分别为
A.50,15 B.50,30 C.30,25 D.25,15
二.多选题(共4小题)
9.一组数据,,,,的平均值为7,方差为4,记,,,,的平均值为,方差为,则
A. B. C. D.
10.某学校为调查高一、高二学生劳动实践活动的情况,对这两个年级的学生分别统计了每周的劳动时间,并制成了如图所示的条形图进行比较.则下列说法中正确的是
A.高二年级学生周劳动时间的众数比高一年级的大
B.高二年级学生周劳动时间的方差比高一年级的大
C.高二年级学生周劳动时间的中位数比高一年级的大
D.高二年级学生周劳动时间的平均值比高一年级的大
11.2020年3月6日,在新加坡举行的世界大学生辩论赛中,中国选手以总分230.51分获得冠军.辩论赛有7位评委进行评分,首先这7位评委给出某对选手的原始分数,评定该队选手的成绩时从7个原始成绩中去掉一个最高分、一个最低分,得到5个有效评分,则5个有效评分与7个原始评分相比,可能变化的数字特征是
A.中位数 B.平均数 C.方差 D.极差
12.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.过去10日,、、、四地新增疑似病例数据信息如下,一定符合没有发生大规模群体感染标志的是
A.地:中位数为2,极差为5
B.地:总体平均数为2,众数为2
C.地:总体平均数为1,总体方差大于0
D.地:总体平均数为2,总体方差为3
三.填空题(共4小题)
13.已知一组数据4,,,5,7的平均数为5,则这组数据的方差为 .
14.2020年初,一场突如其来的新冠疫情给人民的生命安全和身体健康造成严重侵害.全国各地疾控部门迅速行动,某研究所受命对新冠病人的血型进行病理分析,从2500名病人中抽取600人的血液作为样本,已知这2500名病人,,,四大血型的比例为,则抽取的样本中,血型的样本有 人.
15.某中学全体学生参加了“爱北京、爱家乡、爱环境”知识竞赛,现从中随即抽取了50名学生的成绩作为样本进行统计,得到的频率分布直方图如图所示,那么 .
16.已知一组数据,,,的标准差为,数据,,的方差为,则 .
四.解答题(共6小题)
17.某校对120名考生的数学竞赛成绩进行统计,分成,,,,,,,,,五组,得到如图所示频率分布直方图.
(1)求图中的值;
(2)估计该校学生数学竞赛成绩的平均数;
(3)估计该校学生数学竞赛成绩的第80百分位数落在哪一组.
18.2016年某省人社厅推出15项改革措施,包括机关事业单位基本养老保险制度改革、调整机关事业单位工资标准、全省县以下机关建立职务与职级并行制度.某市为了了解该市市民对这些改革措施的态度,在该市随机抽取了50名市民进行调查,作出了他们月收入(单位:百元,范围:,的频率分布直方图,同时得到其中各种月收入情况的市民对该项政策赞成的人数统计表.
月收入 赞成人数
, 4
, 8
, 12
, 5
, 2
, 2
(1)求月收入在百元内的频率,并补全这个频率分布直方图,在图中标出相应的纵坐标;
(2)根据频率分布直方图估计这50人的平均月收入;
(3)为了这个改革方案能够更好的实施,从这些调查者中选取代表提供建议,若从月收入在,百元和,百元的不赞成的被调查者中随机抽取2人,求这两名代表月收入差不超过1000元的概率.
19.高三年级计划从甲、乙两个班中选择一个班参加学校的知识竞赛,设甲班的成绩为,乙班的成绩为,两个班以往6次竞赛的成绩统计如表:
1 2 3 4 5 6
133 145 118 125 132 127
128 139 121 144 127 121
(1)请计算甲、乙两班的平均成绩和方差,从求得数据出发确定派哪个班参加竞赛更合适(方差保留一位小数);
(2)若,则称甲、乙属于“同一阶层”.若从上述6次考试中任取三次,求至少有两次甲、乙属于“同一阶层”的概率.
附:方差.
20.某社区组织了以“共同保护生态环境,共建绿色生态环境家园”为主题的垃圾分类、环境保护宣传咨询服务活动.组织方从参加活动的群众中随机抽取120名群众,按他们的年龄分组:第1组,,第2组,,第3组,,第4组,,第5组,,得到的频率分布直方图如图所示.
(1)若电视台记者要从抽取的群众中选1人进行采访,求被采访人恰好在第2组或第4组的概率;
(2)已知第1组群众中男性有2人,组织方要从第1组中随机抽取2名群众组成宣传志愿者服务小组,求至少有1名男性的概率.
21.为了更好地刺激经济复苏,增加就业岗位,多地政府出台支持“地摊经济”的举措.某市城管委对所在城市约6000个流动商贩进行调查统计,发现所售商品多为小吃、衣帽、玩具、饰品、果蔬等,各类商贩所占比例如图.
(1)该市城管委为了更好地服务百姓,打算从流动商贩中随机抽取100家进行政策问询.如果按照分层抽样的方式抽取,请问果蔬类、小吃类商贩各抽取多少家?
(2)为了更好的了解商贩的收入情况,工作人员对某果蔬商贩最近50天的日收入进行了统计(单位:元),所得频率分布直方图如图所示:
(ⅰ)请根据频率分布直方图估计该果蔬商贩的日平均收入(同一组中的数据用该组区间的中间值代替);
(ⅱ)若从该果蔬商贩这50天中日收入不低于250元的天数中随机抽取2天,求这2天的日收入至少有一天不低于300元的概率.
22.某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如图频率分布直方图,其中时间分组为,,,,,,,,,.
(Ⅰ)求频率分布直方图中的值;
(Ⅱ)从统计学的角度说明学校是否需要推迟5分钟上课;
(Ⅲ)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求这两个学生的单程时间均落在,上的概率.
统计期末单元复习测试题B
参考答案与试题解析
一.选择题(共8小题)
1.【解答】解:由频率分布直方图得:
每周锻炼时间在,小时内的频率为:,
每周锻炼时间在,小时内的人数为:.
故选:.
2.【解答】解:选项,总体均值为1,中位数为1,可能存在某一天超过6人,
例如:前6天0人,天1人,第14天7人,故选项不正确;
选项,总体均值为1,总体标准差大于0,可能存在某一天超过6人,
例如:前13天0人,第14天14人,故选项不正确;
选项,中位数为1,众数为2,可能存在某一天超过6人,
例如:前4天0人,天1人,天2人,第14天8人,故选项不正确;
选项,总体均值为2,总体方差为1,设为当天病例数,,,,
,若,则一定大于1,所以.
故选项正确.
故选:.
3.【解答】解:从表中第1行第9列开始向右依次读取数据,找出4个在内的编号,14,05,11,09,20.
则得到的第4个样本编号09.
故选:.
4.【解答】解:从某市3个区按人口数用分层抽样的方法抽取一个样本.
3个区人口数之比为,且人口最少的一个区抽出100人,
设这个样本的容量为,
则,
解得.
这个样本的容量等于450.
故选:.
5.【解答】解:利用求加权平均数的公式解得:,
故选:.
6.【解答】解:根据题意,一组数据的平均数为,方差为,将这组数据的每个数都乘以得到一组新数据,
则新数据的平均数为,方差为,
则其标准差为,
故选:.
7.【解答】解:由频率分布直方图得:
对于,得分在,之间有:人,故正确;
对于,从这100名参赛者中随机选取1人,其得分在,的概率为:
,故正确;
对于,,解得,故正确;
对于,,的频率为,
,的频率为,
这100名参赛者得分的中位数为:,故错误.
故选:.
8.【解答】解:共有2000户,需要抽取100户,故抽取的比例为,
由统计图可知,衣帽类有500户,果蔬类有300户,
则衣帽类抽样户,果蔬类抽取户.
故选:.
二.多选题(共4小题)
9.【解答】解:,,,,的平均值为7,方差为4,
设,,,,,
,得,
,,
,,,,的平均值为,方差为,
,
,
故选:.
10.【解答】解:由条形统计图得:
对于,高一学生周劳动时间的众数为4,高二学生周劳动时间的众数为5,
高二年级学生周劳动时间的众数比高一年级的大,故正确;
对于,高一年级学生周劳动时间差异相对较大,高二年级的周劳动时间的差异较小,
高二年级学生周劳动时间的方差比高一年级的小,故错误;
对于,高一年级学生周劳动时间的中位数为4,高二年级学生周劳动时间的中位数为5,
高二年级学生周劳动时间的中位数比高一年级的大,故正确;
对于,高一年级学生周劳动时间的平均值为:(小时),
高二年级学生周劳动时间的平均值为:(小时),
高二年级学生周劳动时间的平均值比高一年级的大,故正确.
故选:.
11.【解答】解:因为7个有效评分是9个原始评分中去掉一个最高分、一个最低分,
所以中位数不变,平均数、方差、极差可能发生变化,
所以变化的数字特征是平均数、方差、极差,
故选:.
12.【解答】解:该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.
在地,中位数为2,极差为5,,每天新增疑似病例不会超过7人,所以地符合标准;
在地,总体平均数为2,众数为2,如0,0,0,0,2,2,2,2,2,10,每天新增疑似病例可以超过7人,所以地不符合标准;
在地,总体平均数为1,总体方差大于0,如,0,0,0,0,0,0,0,0,0,10,每天新增疑似病例可以超过7人,所以地不符合标准;
在地,总体平均数为2,总体方差为3.根据方差公式,如果存在大于7的数存在,
根据方差公式,若出现大于7的数值8,则,与总体方差为3矛盾,因而不会出现超过7人的情况,所以地符合标准.
故选:.
三.填空题(共4小题)
13.【解答】解:因为这组数据的平均数为5,
所以,解得,
则这组数为3,4,5,6,7,
故方差.
故答案为:2.
14.【解答】解:根据分层抽样原理知,抽取600人的样本中,
血型的样本数为(人.
故答案为:48.
15.【解答】解:,故.
16.【解答】解:数据,,,的标准差为,
所以数据,,的标准差是,
它的方差是,即,
解方程得或(舍去),
所以.
故答案为:2.
四.解答题(共6小题)
17.【解答】解:(1)由频率分布直方图得:
,
解得.
(2)估计该校学生数学竞赛成绩的平均数为:
.
(3),的频率为,
,的频率为,
估计该校学生数学竞赛成绩的第80百分位数落在,内.
18.【解答】解:(1)月收入在百元内的频率为
;
由,补全这个频率分布直方图,如图所示;
(2)由频率分布直方图,计算平均数为
(百元),
即这50人的平均月收入估计为4300元;
(3),内的人数为15人,其中12人赞成,3人不赞成;
记不赞成的人为,,,;
,内的人数为5人,其中2人赞成,3人不赞成;
记不赞成的3人为,,;
从不赞成的6人中任取2人,基本事件是:
,,,,,,,,,,,,,,共15种情况;
其中两代表月收入差不超过1000元的有,,,,,,共6种情况,
故这两代表月收入不超过1000元的概率是.
19.【解答】解:(1)计算甲班的平均成绩为,
方差为;
乙班的平均成绩为,
方差为;
由于,,所以派甲班参加比赛更合适.
(2)上述6次考试中有1,3,5的成绩为甲、乙属于“同一阶段;
从6次考试中任选三次,总共有:
,2,,,2,,,2,,,2,,,3,,
,3,,,3,,,4,,,4,,,5,,
,3,,,3,,,3,,,4,,,4,,
,5,,,4,,,4,,,5,,,5,共20种结果;
其中至少有两次甲、乙属于“同一阶段”的有:
,2,,,2,,,3,,,3,,,3,,
,4,,,5,,,3,,,4,,,5,共10次;
则至少有两次甲、乙属于“同一阶段”的概率为.
20.【解答】解:(1)第2组的频率为,
第4组的频率为,
所以被采访人恰好在第2组或第4组的概率为;
(2)第1组的频数为,其中男性有2人,女性有4人,
所以从中抽取两名群众,至少有一名男性的概率为.
21.【解答】解:(1)由扇形统计图可知,果蔬类商贩所占比例为,故果蔬类商贩抽取家,
小吃类商贩所占比例为,故小吃类商贩抽取家;
(2)估计该果蔬商贩的日平均收入为:元;
日收入不低于250元的天数为天,
日收入不低于300元的天数为天,
所以这2天的日收入至少有一天不低于300元的概率为.
22.【解答】解:(1)时间分组为,的频率为:
,
.
(2)100个非住校生上学路上单程所需时间的平均数为:
.
,该校不需要推迟5分钟上课.
(3)从单程所需时间不小于30分钟的5名学生中,随机抽取2人共有以下10种情况:
,,,,,,,,,,
,,,,,,,,,,
其中恰有一个学生的单程所需时间落在,中的有以下3种:,,,,,;
两个学生的单程时间均落在,上的概率为.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
