等腰三角形的性质 说课课件
文档属性
| 名称 | 等腰三角形的性质 说课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 199.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-06 21:37:27 | ||
图片预览







文档简介
(共24张PPT)
课题名称:
等腰三角形的性质
教学目标:
(1)掌握等腰三角形的性质及三线合一。
(2)通过折纸实验探索等腰三角形的性质,让学生进一步经历观察、实验、归纳、推理、交流等活动,体验数学证明的必要性,培养学生数学说理的习惯。
(3)通过例题的教学,学会利用多种方法求解几何问题,培养学生学数学应用数学的意识及一题多解的能力。
本节重点:
灵活掌握等腰三角形的性质
本节难点:
如何添加辅助线,等腰三角形“三线合一”性质的灵活运用。
首先让学生举出一些等腰三角形在
日常生活中应用的例子吗?学生举例后
教师设置疑问等腰三角形在日常生活中为什么
能应用的如此广泛能呢?
他到底具有那些性质呢?
让学生在一张半透明的纸上任意画一个等腰三角形,命名为△ABC,将△ABC剪下来,然后将三角形纸片对折,让两腰AB、AC重叠在一起,折痕为AD,你能发现什么?尽可能多的写出结论。
结论:
(1)等腰三角形是轴对称图形
(2)∠B=∠C
(3)BD=CD即AD是底边上的中线
(4)∠ADB=∠ADC=90度即AD是底边上的高
(5)∠BAD=∠CAD即AD是顶角平分线
在学生得出以上结论基础上,
教师提出你能将结论(2)用文字表述吗?
学生概括得出等腰三角形的两个底角相等。
结论(3)、(4)、(5)可以用一句话概括为什么?
议一议:
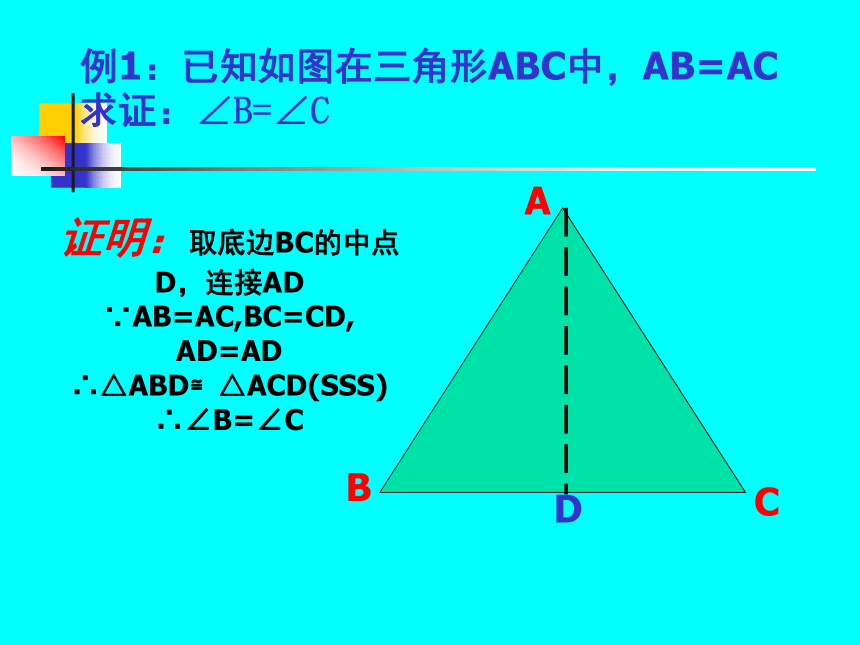
例1:已知如图在三角形ABC中,AB=AC
求证:∠B=∠C
A
B
C
D
证明:取底边BC的中点D,连接AD
∵AB=AC,BC=CD, AD=AD
∴△ABD≌△ACD(SSS)
∴∠B=∠C
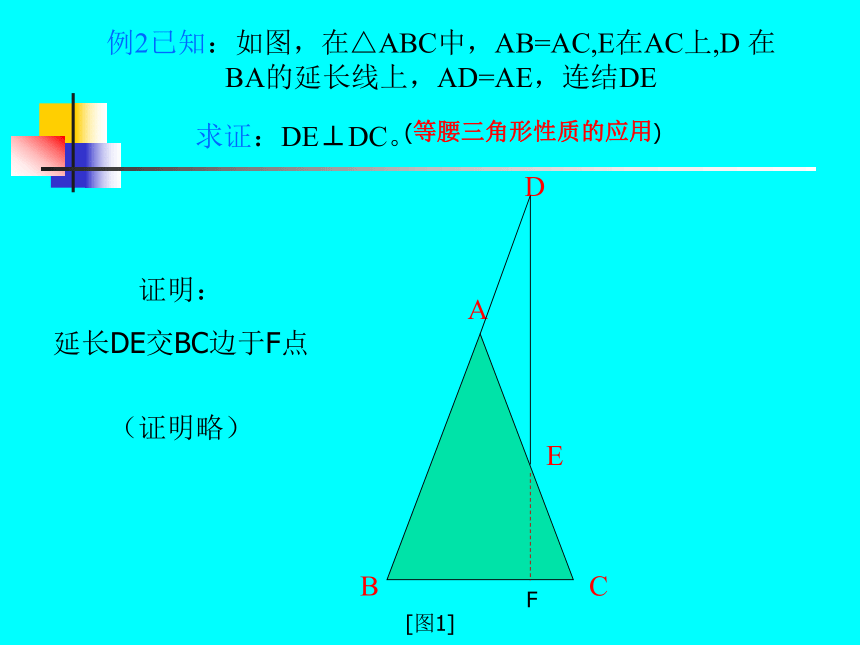
例2已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE
求证:DE⊥DC。
D
A
B
C
E
F
[图1]
证明:
延长DE交BC边于F点
(证明略)
(等腰三角形性质的应用)
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
D
A
B
C
E
N
证明:
过C点做AB的平行线,交DE的延长线于N点
(证明略)
[图2]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
D
A
B
C
E
F
G
证明:
过B点做AC的平行线,交DE的延长线于G点
(证明略)
[图3]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过B点做DE的平行线,交CA的延长线于Q点
(证明略)
D
A
B
C
E
Q
[图4]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过C点做DE的平行线,交BA的延长线于R点
(证明略)
D
A
B
C
E
R
[图5]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过A点做BC的平行线,交DE于P点
(证明略)
D
A
B
C
E
P
[图6]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过D点做AC的平行线,交BC的延长线于H点,并延长DE交BC于F点
(证明略)
D
A
B
E
F
C
H
[图7]
D
A
B
C
E
D
A
B
C
E
A
B
C
E
D
A
B
C
E
除了第一种辅助线的作法外,
大部分同学能发现其余的辅助线都是
作了AB的平行线,AC的平形线,
BC的平行线和DE的平行线,。
D
A
B
C
E
D
A
B
C
E
课堂练习
1。如图,在△ABD中,C是BD上的一点,
且AC⊥BD,AC=BC=CD,
A
B
D
C
(1)求证:△ABD是等腰三角形;
(2)求∠ABD的度数。
1、等腰三角形的两条性质:“等边对等角”,“三线合一”。
2、已知等腰三角形一个角(或一条边)时,要注意分类讨论,判断是顶角还是底角(是腰还是底边)。
3、注意:等边对等角是指在一个三角形内用的。
课堂小结:
当堂检测:
1。已知,如图,AB=AC,BD⊥AC于D,
求证:∠BAC=2∠DBC
A
B
C
D
发散思考:
此题是否可以通过加倍∠CBD,
另作∠FBD=∠CBD?
(2)已知:如图,△ABC中,AB=AC,D点在AB上,E点在AC的延长线上,且BD=CE,连结DE,交BC于F
求证:DF=EF
A
B
C
E
D
F
发散思考:
如果把已知中的BD=CE与结论DF=EF互换,而其它条件不变,那此题是否成立?
请领导多多加以指导!
课题名称:
等腰三角形的性质
教学目标:
(1)掌握等腰三角形的性质及三线合一。
(2)通过折纸实验探索等腰三角形的性质,让学生进一步经历观察、实验、归纳、推理、交流等活动,体验数学证明的必要性,培养学生数学说理的习惯。
(3)通过例题的教学,学会利用多种方法求解几何问题,培养学生学数学应用数学的意识及一题多解的能力。
本节重点:
灵活掌握等腰三角形的性质
本节难点:
如何添加辅助线,等腰三角形“三线合一”性质的灵活运用。
首先让学生举出一些等腰三角形在
日常生活中应用的例子吗?学生举例后
教师设置疑问等腰三角形在日常生活中为什么
能应用的如此广泛能呢?
他到底具有那些性质呢?
让学生在一张半透明的纸上任意画一个等腰三角形,命名为△ABC,将△ABC剪下来,然后将三角形纸片对折,让两腰AB、AC重叠在一起,折痕为AD,你能发现什么?尽可能多的写出结论。
结论:
(1)等腰三角形是轴对称图形
(2)∠B=∠C
(3)BD=CD即AD是底边上的中线
(4)∠ADB=∠ADC=90度即AD是底边上的高
(5)∠BAD=∠CAD即AD是顶角平分线
在学生得出以上结论基础上,
教师提出你能将结论(2)用文字表述吗?
学生概括得出等腰三角形的两个底角相等。
结论(3)、(4)、(5)可以用一句话概括为什么?
议一议:
例1:已知如图在三角形ABC中,AB=AC
求证:∠B=∠C
A
B
C
D
证明:取底边BC的中点D,连接AD
∵AB=AC,BC=CD, AD=AD
∴△ABD≌△ACD(SSS)
∴∠B=∠C
例2已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE
求证:DE⊥DC。
D
A
B
C
E
F
[图1]
证明:
延长DE交BC边于F点
(证明略)
(等腰三角形性质的应用)
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
D
A
B
C
E
N
证明:
过C点做AB的平行线,交DE的延长线于N点
(证明略)
[图2]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
D
A
B
C
E
F
G
证明:
过B点做AC的平行线,交DE的延长线于G点
(证明略)
[图3]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过B点做DE的平行线,交CA的延长线于Q点
(证明略)
D
A
B
C
E
Q
[图4]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过C点做DE的平行线,交BA的延长线于R点
(证明略)
D
A
B
C
E
R
[图5]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过A点做BC的平行线,交DE于P点
(证明略)
D
A
B
C
E
P
[图6]
已知:如图,在△ABC中,AB=AC,E在AC上,D 在BA的延长线上,AD=AE,连结DE。
求证:DE⊥DC。
证明:
过D点做AC的平行线,交BC的延长线于H点,并延长DE交BC于F点
(证明略)
D
A
B
E
F
C
H
[图7]
D
A
B
C
E
D
A
B
C
E
A
B
C
E
D
A
B
C
E
除了第一种辅助线的作法外,
大部分同学能发现其余的辅助线都是
作了AB的平行线,AC的平形线,
BC的平行线和DE的平行线,。
D
A
B
C
E
D
A
B
C
E
课堂练习
1。如图,在△ABD中,C是BD上的一点,
且AC⊥BD,AC=BC=CD,
A
B
D
C
(1)求证:△ABD是等腰三角形;
(2)求∠ABD的度数。
1、等腰三角形的两条性质:“等边对等角”,“三线合一”。
2、已知等腰三角形一个角(或一条边)时,要注意分类讨论,判断是顶角还是底角(是腰还是底边)。
3、注意:等边对等角是指在一个三角形内用的。
课堂小结:
当堂检测:
1。已知,如图,AB=AC,BD⊥AC于D,
求证:∠BAC=2∠DBC
A
B
C
D
发散思考:
此题是否可以通过加倍∠CBD,
另作∠FBD=∠CBD?
(2)已知:如图,△ABC中,AB=AC,D点在AB上,E点在AC的延长线上,且BD=CE,连结DE,交BC于F
求证:DF=EF
A
B
C
E
D
F
发散思考:
如果把已知中的BD=CE与结论DF=EF互换,而其它条件不变,那此题是否成立?
请领导多多加以指导!
