冀教版七年级数学下册同步练习:7.4 平行线的判定(Word版 含答案)
文档属性
| 名称 | 冀教版七年级数学下册同步练习:7.4 平行线的判定(Word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 656.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 16:19:38 | ||
图片预览


文档简介
7.4 平行线的判定
一、选择题
1.不能判定两直线平行的条件是( )
A.同位角相等
B.内错角相等
C.同旁内角相等
D.垂直于平面内同一条直线
2.如图1,D,B,C三点在同一条直线上,下列能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠A=∠ABE
图1
图2
3.已知如图2,直线a,b被直线c所截,下列条件能判定a∥b的是( )
A.∠1=∠3
B.∠2=∠3
C.∠1=∠4
D.∠2+∠5=180°
4.下列图形中,由∠1=∠2能得到AB∥CD的是( )
图3
5.如图4,点A,D,E在一条直线上,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB∥DC的条件为( )
图4
A.①④
B.②③
C.①③
D.①③④
6.如图5,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB,AC,AE,ED,EC,DB中,相互平行的线段有( )
图5
A.4组
B.3组
C.2组
D.1组
二、填空题
7.如图6,小明利用两块相同的三角尺,沿三角尺的边缘画平行线AB和CD,这是根据____________,两直线平行.
图6
图7
8.2018·湘潭
如图7,E是AD延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为________.(任意添加一个符合题意的条件即可)
9.如图8,∠1=∠2,∠2=∠C,则图中互相平行的直线有________.
图8
图9
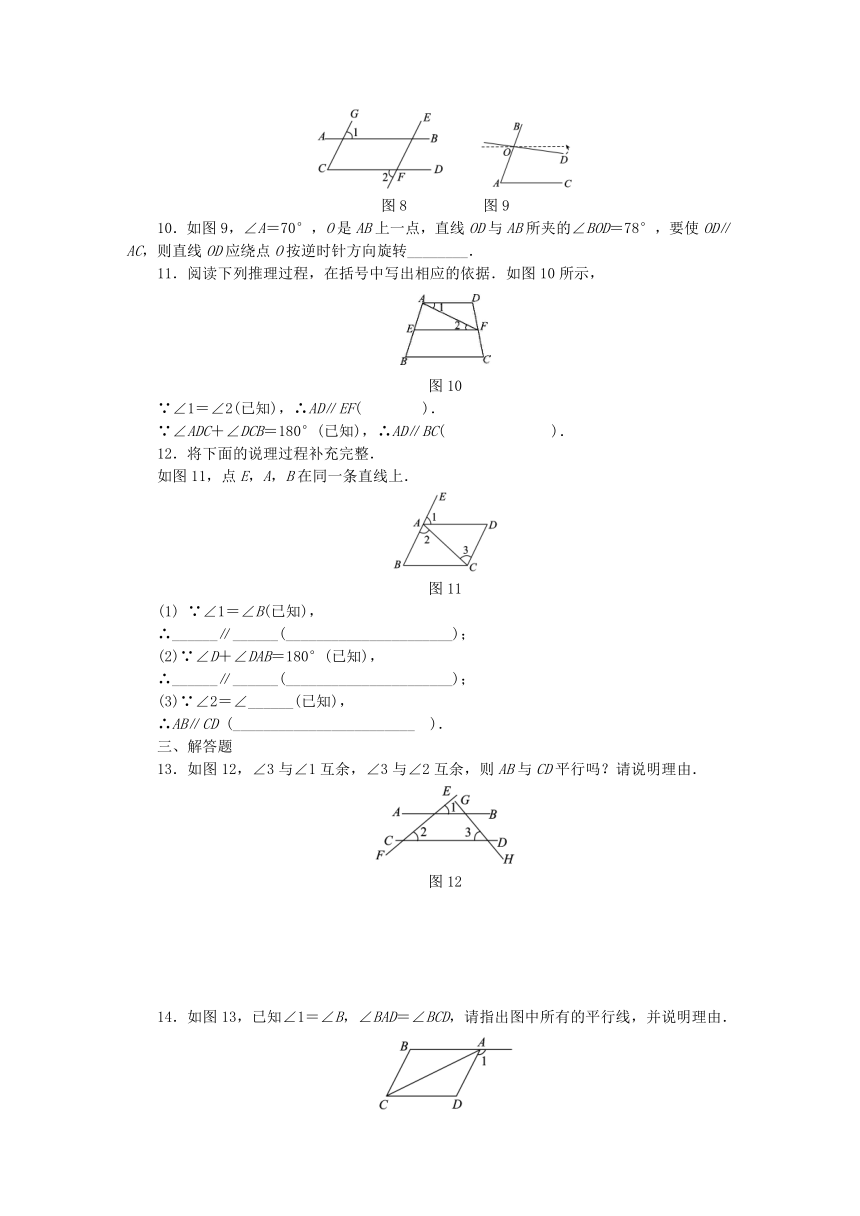
10.如图9,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,则直线OD应绕点O按逆时针方向旋转________.
11.阅读下列推理过程,在括号中写出相应的依据.如图10所示,
图10
∵∠1=∠2(已知),∴AD∥EF( ).
∵∠ADC+∠DCB=180°(已知),∴AD∥BC( ).
12.将下面的说理过程补充完整.
如图11,点E,A,B在同一条直线上.
图11
(1)
∵∠1=∠B(已知),
∴______∥______(______________________);
(2)∵∠D+∠DAB=180°(已知),
∴______∥______(______________________);
(3)∵∠2=∠______(已知),
∴AB∥CD
(________________________
).
三、解答题
13.如图12,∠3与∠1互余,∠3与∠2互余,则AB与CD平行吗?请说明理由.
图12
14.如图13,已知∠1=∠B,∠BAD=∠BCD,请指出图中所有的平行线,并说明理由.
图13
15.如图14,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
图14
16.如图15,E,A,D三点在一条直线上,要想判断AB是否与CD平行,我们可以测量哪些角?请你写出三种方案,并说明理由.
图15
17我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.图16是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3.请你用所学知识来判断直线c与d是否平行,并说明理由.
图16
1.C
2.D [解析]
观察四个选项,只有第四个选项中的两个角是EB和AC被AB所截形成的内错角,根据内错角相等,两直线平行,可判定EB∥AC.
3.A [解析]
因为∠1=∠3(已知),所以a∥b(内错角相等,两直线平行).而∠2=∠3,∠1=∠4,∠2+∠5=180°都不能判定a∥b.
4.B
5.D [解析]
①因为∠1=∠2,所以AB∥CD,故本选项符合题意;②因为∠3=∠4,所以BC∥AD,故本选项不符合题意;③因为∠A=∠CDE,所以AB∥CD,故本选项符合题意;④因为∠A+∠ADC=180°,所以AB∥CD,故本选项符合题意.故选D.
6.B [解析]
由完全相等的三角板的对应角相等可得出角的等量关系,从而得到答案.
7.内错角相等
8.答案不唯一,如∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.
9.EF∥CG,AB∥CD [解析]
因为∠2=∠C,所以EF∥CG(内错角相等,两直线平行).又因为∠1=∠2,所以∠1=∠C,所以AB∥CD(同位角相等,两直线平行).
10.8°
11.内错角相等,两直线平行
同旁内角互补,两直线平行
12.(1)AD BC 同位角相等,两直线平行
(2)
AB CD 同旁内角互补,两直线平行
(3)3 内错角相等,两直线平行
13.解:AB∥CD.
理由:因为∠3与∠1互余,∠3与∠2互余,即∠3+∠1=90°,∠3+∠2=90°,所以∠1=∠2,所以AB∥CD.
14.解:平行线:AD∥BC,AB∥CD.
理由如下:因为∠1=∠B,所以AD∥BC.
因为∠BAD=∠BCD,∠1+∠BAD=180°,
所以∠B+∠BCD=180°,所以AB∥CD.
15.解:OB∥AC,OA∥BC.
理由:因为∠1=50°,∠2=50°,
所以∠1=∠2,所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°,所以OA∥BC.
16.解:方案一:可以测量∠EAB与∠D的度数,如果∠EAB=∠D,那么根据同位角相等,两直线平行,可得出AB与CD平行.
方案二:可以测量∠BAC与∠C的度数,如果∠BAC=∠C,那么根据内错角相等,两直线平行,可得出AB与CD平行.
方案三:可以测量∠BAD与∠D的度数,如果∠BAD+∠D=180°,那么根据同旁内角互补,两直线平行,可得出AB与CD平行.
17
解:c∥d.理由如下:
如图,因为∠1+∠5=∠4+∠6,∠1=∠4,所以∠5=∠6.
因为∠2=∠3,所以∠2+∠5=∠3+∠6(等式的性质),
所以∠1+∠7=∠4+∠8,所以c∥d(内错角相等,两直线平行).
一、选择题
1.不能判定两直线平行的条件是( )
A.同位角相等
B.内错角相等
C.同旁内角相等
D.垂直于平面内同一条直线
2.如图1,D,B,C三点在同一条直线上,下列能判定EB∥AC的条件是( )
A.∠C=∠ABE
B.∠A=∠EBD
C.∠C=∠ABC
D.∠A=∠ABE
图1
图2
3.已知如图2,直线a,b被直线c所截,下列条件能判定a∥b的是( )
A.∠1=∠3
B.∠2=∠3
C.∠1=∠4
D.∠2+∠5=180°
4.下列图形中,由∠1=∠2能得到AB∥CD的是( )
图3
5.如图4,点A,D,E在一条直线上,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB∥DC的条件为( )
图4
A.①④
B.②③
C.①③
D.①③④
6.如图5,将三个相同的三角尺不重叠不留空隙地拼在一起,观察图形,在线段AB,AC,AE,ED,EC,DB中,相互平行的线段有( )
图5
A.4组
B.3组
C.2组
D.1组
二、填空题
7.如图6,小明利用两块相同的三角尺,沿三角尺的边缘画平行线AB和CD,这是根据____________,两直线平行.
图6
图7
8.2018·湘潭
如图7,E是AD延长线上一点,如果添加一个条件,使BC∥AD,那么可添加的条件为________.(任意添加一个符合题意的条件即可)
9.如图8,∠1=∠2,∠2=∠C,则图中互相平行的直线有________.
图8
图9
10.如图9,∠A=70°,O是AB上一点,直线OD与AB所夹的∠BOD=78°,要使OD∥AC,则直线OD应绕点O按逆时针方向旋转________.
11.阅读下列推理过程,在括号中写出相应的依据.如图10所示,
图10
∵∠1=∠2(已知),∴AD∥EF( ).
∵∠ADC+∠DCB=180°(已知),∴AD∥BC( ).
12.将下面的说理过程补充完整.
如图11,点E,A,B在同一条直线上.
图11
(1)
∵∠1=∠B(已知),
∴______∥______(______________________);
(2)∵∠D+∠DAB=180°(已知),
∴______∥______(______________________);
(3)∵∠2=∠______(已知),
∴AB∥CD
(________________________
).
三、解答题
13.如图12,∠3与∠1互余,∠3与∠2互余,则AB与CD平行吗?请说明理由.
图12
14.如图13,已知∠1=∠B,∠BAD=∠BCD,请指出图中所有的平行线,并说明理由.
图13
15.如图14,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,并说明理由.
图14
16.如图15,E,A,D三点在一条直线上,要想判断AB是否与CD平行,我们可以测量哪些角?请你写出三种方案,并说明理由.
图15
17我们知道,光线从空气射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.图16是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3.请你用所学知识来判断直线c与d是否平行,并说明理由.
图16
1.C
2.D [解析]
观察四个选项,只有第四个选项中的两个角是EB和AC被AB所截形成的内错角,根据内错角相等,两直线平行,可判定EB∥AC.
3.A [解析]
因为∠1=∠3(已知),所以a∥b(内错角相等,两直线平行).而∠2=∠3,∠1=∠4,∠2+∠5=180°都不能判定a∥b.
4.B
5.D [解析]
①因为∠1=∠2,所以AB∥CD,故本选项符合题意;②因为∠3=∠4,所以BC∥AD,故本选项不符合题意;③因为∠A=∠CDE,所以AB∥CD,故本选项符合题意;④因为∠A+∠ADC=180°,所以AB∥CD,故本选项符合题意.故选D.
6.B [解析]
由完全相等的三角板的对应角相等可得出角的等量关系,从而得到答案.
7.内错角相等
8.答案不唯一,如∠A+∠ABC=180°或∠C+∠ADC=180°或∠CBD=∠ADB或∠C=∠CDE.
9.EF∥CG,AB∥CD [解析]
因为∠2=∠C,所以EF∥CG(内错角相等,两直线平行).又因为∠1=∠2,所以∠1=∠C,所以AB∥CD(同位角相等,两直线平行).
10.8°
11.内错角相等,两直线平行
同旁内角互补,两直线平行
12.(1)AD BC 同位角相等,两直线平行
(2)
AB CD 同旁内角互补,两直线平行
(3)3 内错角相等,两直线平行
13.解:AB∥CD.
理由:因为∠3与∠1互余,∠3与∠2互余,即∠3+∠1=90°,∠3+∠2=90°,所以∠1=∠2,所以AB∥CD.
14.解:平行线:AD∥BC,AB∥CD.
理由如下:因为∠1=∠B,所以AD∥BC.
因为∠BAD=∠BCD,∠1+∠BAD=180°,
所以∠B+∠BCD=180°,所以AB∥CD.
15.解:OB∥AC,OA∥BC.
理由:因为∠1=50°,∠2=50°,
所以∠1=∠2,所以OB∥AC.
因为∠2=50°,∠3=130°,
所以∠2+∠3=180°,所以OA∥BC.
16.解:方案一:可以测量∠EAB与∠D的度数,如果∠EAB=∠D,那么根据同位角相等,两直线平行,可得出AB与CD平行.
方案二:可以测量∠BAC与∠C的度数,如果∠BAC=∠C,那么根据内错角相等,两直线平行,可得出AB与CD平行.
方案三:可以测量∠BAD与∠D的度数,如果∠BAD+∠D=180°,那么根据同旁内角互补,两直线平行,可得出AB与CD平行.
17
解:c∥d.理由如下:
如图,因为∠1+∠5=∠4+∠6,∠1=∠4,所以∠5=∠6.
因为∠2=∠3,所以∠2+∠5=∠3+∠6(等式的性质),
所以∠1+∠7=∠4+∠8,所以c∥d(内错角相等,两直线平行).
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
