不等式与不等关系（1）

(共13张PPT)
§3.1.1不等关系与不等式（一）
认识不等式
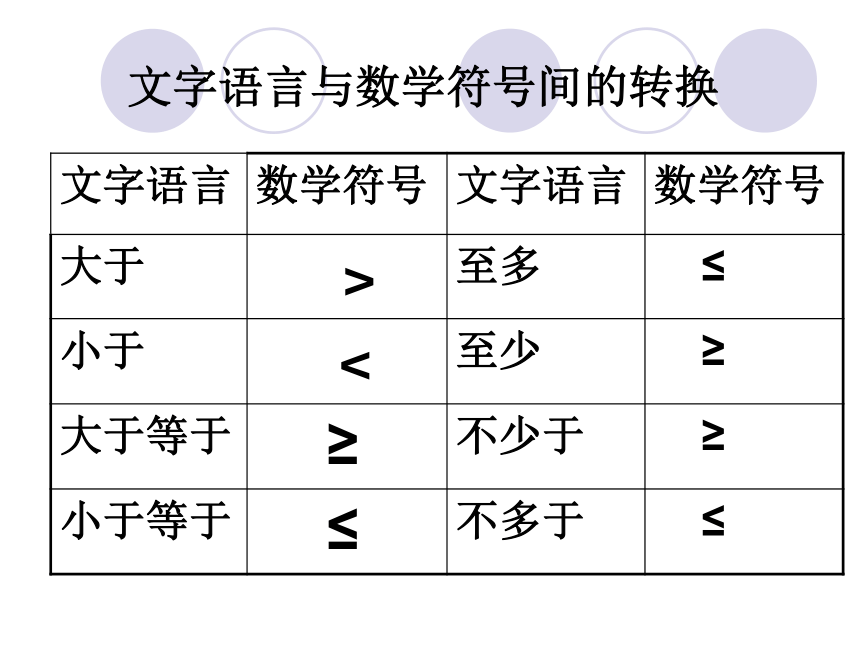
文字语言与数学符号间的转换
文字语言 数学符号 文字语言 数学符号
大于 > 至多 ≤
小于 < 至少 ≥
大于等于 ≥ 不少于 ≥
小于等于 ≤ 不多于 ≤
§3.1.1不等关系与不等式（一）
问题1：设点A与平面的距离为d，B为平面上的任意一点，则
问题2：某种杂志原以每本2.5元的价格销售，可以售出8万本。根据市场调查，若单价每提高0.1元，销售量就可能相应减少0.2万本。若把提价后杂志的定价设为x元，怎样用不等式表示销售的总收入仍不低于20万元？
d≤┃AB┃。
§3.1.1不等关系与不等式（一）
问题3：某钢铁厂要把长度为4000mm的钢管截成500mm和600mm两种，按照生产的要求，600mm钢管的数量不能超过500mm钢管的3倍。怎样写出满足上述所有不等关系的不等式呢？
根据题意，应有如下的不等关系：
（1）解得两种钢管的总长度不能超过4000mm；
（2）截得600mm钢管的数量不能超过500mm
钢管数量的3倍；
（3）解得两钟钢管的数量都不能为负。
§3.1.1不等关系与不等式（一）
由以上不等关系，可得不等式组：
§3.1.1不等关系与不等式（一）
例1：某校学生以面粉和大米为主食．已知面食每100克含蛋白质6个单位，含淀粉4个单位；米饭每100克含蛋白质3个单位，含淀粉7个单位．某快餐公司给学生配餐，现要求每盒至少含8个单位的蛋白质和10个单位的淀粉．设每盒快餐需面食x百克、米饭y百克，试写出x,y满足的条件．
§3.1.1不等关系与不等式（一）
例2：配制A,B两种药剂需要甲、乙两种原料，已知配一剂A种药需甲料3毫克，乙料5毫克，配一剂B种药需甲料5毫克，乙料4毫克。今有甲料20毫克，乙料25毫克，若A，B两种药至少各配一剂，则A，B两种药在配制时应满足怎样的不等关系
§3.1.1不等关系与不等式（一）
知识拓展
从实数的基本性质出发，实数的运算性质与大小顺序之间的关系：对于任意两个实数a,b,
如果a>b,那么a-b是正数; 如果a如果a-b等于0.
§3.1.1不等关系与不等式（一）
（1）如果a>b,那么a-b是正数;
☆（2）如果a（3）如果a-b等于0.那么a=b.
§3.1.1不等关系与不等式（一）
例3、比较(a＋3)（a－５）与
（a＋2）（a－4）的大小.
例4、已知x≠0，比较
与 的大小.
§3.1.1不等关系与不等式（一）
归纳：作差比较法的步骤是：
1、作差；
2、变形：配方、因式分解、通分、分母（分子）有理化等；
3、判断符号；
4、作出结论．
§3.1.1不等关系与不等式（一）
作业：