12.2.2用坐标表示轴对称
文档属性
| 名称 | 12.2.2用坐标表示轴对称 |  | |
| 格式 | zip | ||
| 文件大小 | 163.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-07 07:15:57 | ||
图片预览








文档简介
(共31张PPT)
学习目标: 1、掌握在平面直角坐标系中,关于x轴和y轴对称点的坐标特点,并能运用它解决简单的问题; 2、能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形。
12.2.2
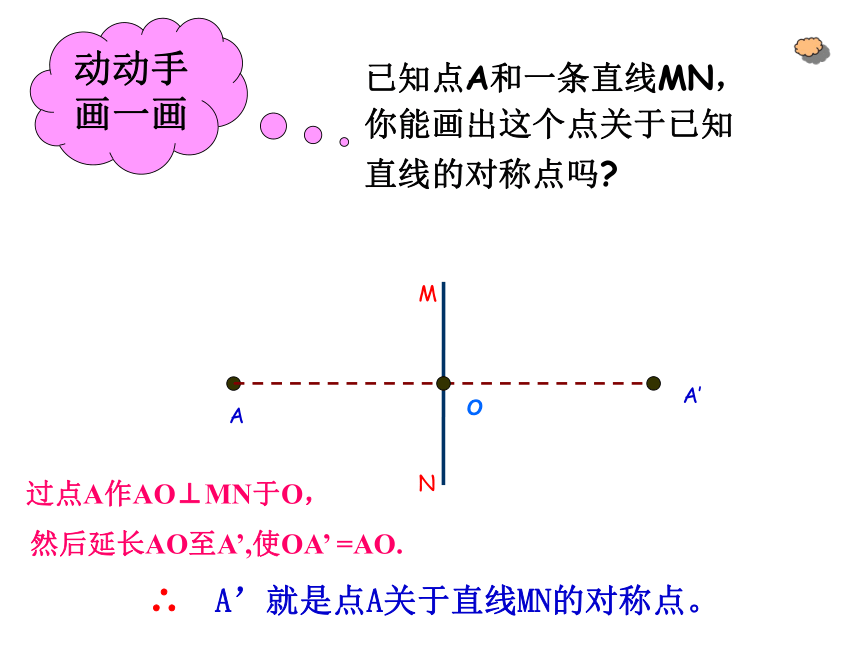
动动手画一画
已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A’
M
N
∴ A’就是点A关于直线MN的对称点。
O
然后延长AO至A’,使OA’ =AO.
过点A作AO⊥MN于O,
0
1
2
3
4
5
-4
-3
-2
-1
x
·
·
·
·
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
y
·
·
A1
B1
D1
C1
·
·
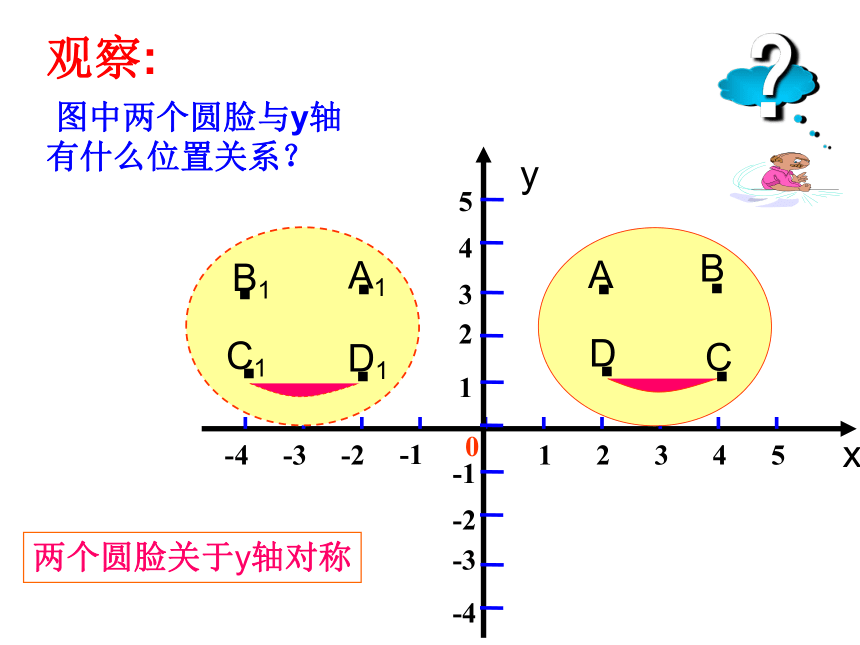
观察:
图中两个圆脸与y轴
有什么位置关系?
?
两个圆脸关于y轴对称
探究1:如图,在平面直角坐标系中你能画出点A关于x轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(2,-3)
你能说出点A与点A’坐标的关系吗?
请在坐标系中多找几个点,
并画出它们关于轴对称的点,
然后观察已知点与对称点的横坐标和纵坐标有什么变化
在平面直角坐标系中画出下列各点关于x轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (-4, -2)
·
C’(3, 4)
思考:关于x轴对称的点的坐标具有怎样的关系?
通过探究你能用语言归纳关于 x 轴对称的点坐标规律吗?
归纳:关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练习:
1、点P(-5, 6)与点Q关于x轴对称,
则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于x轴对称,
则a=_____, b =_____.
(- 5 , -6 )
-2
5
探究2:如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(-2,3)
你能说出点A与点A’坐标的关系吗?
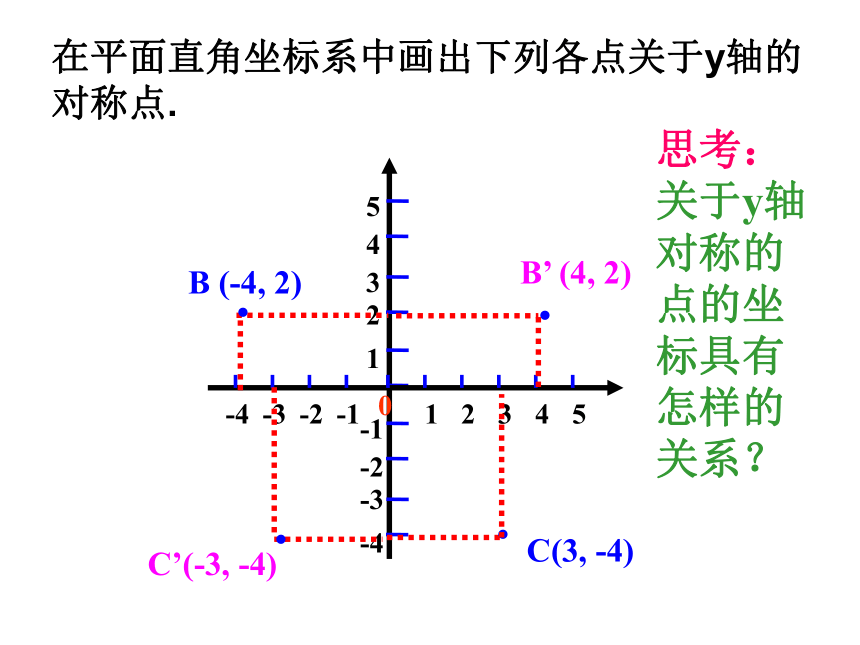
在平面直角坐标系中画出下列各点关于y轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (4, 2)
·
C’(-3, -4)
思考:关于y轴对称的点的坐标具有怎样的关系?
归纳:关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练习:
1、点P(-5, 6)与点Q关于y轴对称,
则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于y轴对称,
则a=_____, b =_____.
( 5 , 6 )
2
-5
小结:在平面直角坐标系中,
关于x轴对称的点横坐标相等,纵坐标互为相反数.
关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
y
已知点
关于x轴的对称点
关于y轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
A′(2,3)
A″( -2,-3 )
B′( -1,-2)
B″( 1,2)
C′( -6,5 )
C″( 6,-5)
E′( -4,0 )
E″( 4,0 )
E(4,0)
x
在图中,画出已知点及其对称点,并把坐标填入表格中.
[P43]
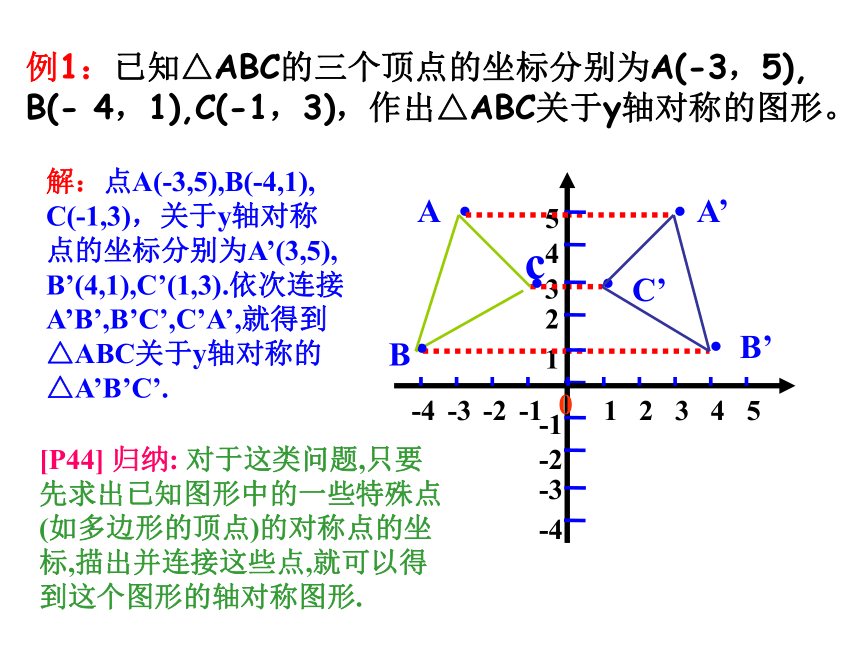
例1:已知△ABC的三个顶点的坐标分别为A(-3,5), B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
[P44] 归纳: 对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
例2:四边形ABCD的四个顶点的坐标分别是
A(-5,1), B(-2,1),
C(-2,5), D(-5,4),
分别作出与四边形ABCD关于y轴和x轴对称的图形.
x
y
0
A
B
C
D
A′
B′
C′
D′
对于这类问题,只要先求出已知图形
中的一些特殊点的对称点的坐标,
描出并连结这些点,就可以得到这
个图形的轴对称图形.
1、完成下表. [P44]
已知点 (-2,6) (1,-2) (-1,3) (-4,-2) (1,0)
关于x轴的对称点
关于y轴的对称点
(2,6)
(-2,-6)
(1,-2)
(-1,-2)
(1,3)
(-1,-3)
(4,-2)
(-4,2)
(-1,0)
(1,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
[练习]: P45:2,3。
(1,2)
·
·
·
·
·
·
[P46:7]如图,小球起始时位于(3,0),沿所示的方向击球,小球运动轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上关于直线l对称的点.如果小球起始时位于(1,0)处,仍按原来的方向击球,请你画出这时小球运动的轨迹.
o
1
2
3
4
5
6
7
8
1
2
3
4
l
探究3:如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,3)
思考:
1、在平面直角坐标系中,点(x,y)关于直线x=1对称点的坐标是多少
2、在平面直角坐标系中,点(x, y)关于直线x=-1对称点的坐标是多少
3、在平面直角坐标系中,点(x,y)关于直线y=1对称点的坐标是多少
4、在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是多少
(-x+2,y)
(-x-2,y)
(x,-y+2)
(x,-y-2)
类似: 若两点(x1,y1)、(x2,y2)关于
直线y=n对称,则 ,n=
归纳: 若两点(x1,y1)、(x2,y2)关于
直线x=m对称,则m= , .
y1=y2
x1=x2
小组合作交流
点(a,b)关于直线x=m对称的点坐标为多少?
点(a,b)关于直线y=n对称的点坐标为多少?
1、学习了在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点。
这节课你学到了什么?
关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
作业:
完成P45第2-4题 。
谢谢指导!再见!
⒈ 快速口答
(3,6)(-7,9)关于x轴的对称点;
(-3,-5)(0,10)关于y轴的对称点.
2.根据下列点的坐标的变化,判断它们进
行了怎样的变换:
⑴(-1,3) (-1,-3)
⑵(-5,-4) (-5,4)
⑶(3,4) (-3,4)
⑷(1,0) (-1,0)
3、 如图所示的点A 、B、 C、 D 、E中,哪两个点关于x轴对称 哪两个点关于y轴对称
x
y
A
B
C
D
E
课堂检测
1、点(1,2)关于x轴的对称点是 —————,关于y轴的对称点是________.
2、点(-3,4)关于直线x=2的对称点是____.
3、已知点(x,4-y)与点(1-y,2x)关于y轴对称,则xy= ————————。
4、已知点M(3,y)在直线y= -x+1上,则点M关于x轴的对称点是__________.
7.已知点D在△ABC的边AB的垂直平分线上,且AD+DC=AC,若AC=5cm,BC=4cm,则△BDC的周长为( )
A、6cm B、7cm
C、8cm D、9cm
8.线段AB外有两点C,D(在AB同侧)使CA=CB,DA=DB,∠ADB=80°, ∠CAD=10°,则∠ACB=( )
A.90° B.100° C.110° D.120°
9.BD为CE的中垂线,A在CB延长线上,∠C=34°,则∠ABE=( )
A.17° B.34° C.68° D.136°
10. P在 AOB内;点M,N分别是点P关于AO,BO的对称点,且与AO、BO相交点E、F,若PEF的周长为15,求MN的长.
11.在由小正方形组成的L形的图中,用三种不同方法添画一个小正方形,使它成为轴对称图形。
12.在Rt△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD∶∠BAC=1∶3,求∠B的度数。
13.已知:在△ABC中,AB<AC,BC边上的垂直平分DE交BC于点D,交AC于点E,AC=8cm,△ABE的周长是14cm,求AB的长。
学习目标: 1、掌握在平面直角坐标系中,关于x轴和y轴对称点的坐标特点,并能运用它解决简单的问题; 2、能在平面直角坐标系中画出一些简单的关于x轴和y轴的对称图形。
12.2.2
动动手画一画
已知点A和一条直线MN,你能画出这个点关于已知直线的对称点吗
A
A’
M
N
∴ A’就是点A关于直线MN的对称点。
O
然后延长AO至A’,使OA’ =AO.
过点A作AO⊥MN于O,
0
1
2
3
4
5
-4
-3
-2
-1
x
·
·
·
·
A
B
C
D
3
1
4
2
5
-2
-4
-1
-3
y
·
·
A1
B1
D1
C1
·
·
观察:
图中两个圆脸与y轴
有什么位置关系?
?
两个圆脸关于y轴对称
探究1:如图,在平面直角坐标系中你能画出点A关于x轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(2,-3)
你能说出点A与点A’坐标的关系吗?
请在坐标系中多找几个点,
并画出它们关于轴对称的点,
然后观察已知点与对称点的横坐标和纵坐标有什么变化
在平面直角坐标系中画出下列各点关于x轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (-4, -2)
·
C’(3, 4)
思考:关于x轴对称的点的坐标具有怎样的关系?
通过探究你能用语言归纳关于 x 轴对称的点坐标规律吗?
归纳:关于x轴对称的点的坐标的特点是:
横坐标相等,纵坐标互为相反数.
练习:
1、点P(-5, 6)与点Q关于x轴对称,
则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于x轴对称,
则a=_____, b =_____.
(- 5 , -6 )
-2
5
探究2:如图,你能在平面直角坐标系中画出点A关于y轴的对称点吗
·
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
A (2,3)
·
A’(-2,3)
你能说出点A与点A’坐标的关系吗?
在平面直角坐标系中画出下列各点关于y轴的对称点.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
B (-4, 2)
·
·
C(3, -4)
·
B’ (4, 2)
·
C’(-3, -4)
思考:关于y轴对称的点的坐标具有怎样的关系?
归纳:关于y轴对称的点的坐标的特点是:
横坐标互为相反数,纵坐标相等.
练习:
1、点P(-5, 6)与点Q关于y轴对称,
则点Q的坐标为__________.
2、点M(a, -5)与点N(-2, b)关于y轴对称,
则a=_____, b =_____.
( 5 , 6 )
2
-5
小结:在平面直角坐标系中,
关于x轴对称的点横坐标相等,纵坐标互为相反数.
关于y轴对称的点横坐标互为相反数,纵坐标相等.
点(x, y)关于x轴对称的点的坐标为______.
点(x, y)关于y轴对称的点的坐标为______.
(x, - y)
(- x, y)
y
已知点
关于x轴的对称点
关于y轴的对称点
A(2,-3)
B(-1,2)
C(-6,-5)
A′(2,3)
A″( -2,-3 )
B′( -1,-2)
B″( 1,2)
C′( -6,5 )
C″( 6,-5)
E′( -4,0 )
E″( 4,0 )
E(4,0)
x
在图中,画出已知点及其对称点,并把坐标填入表格中.
[P43]
例1:已知△ABC的三个顶点的坐标分别为A(-3,5), B(- 4,1),C(-1,3),作出△ABC关于y轴对称的图形。
解:点A(-3,5),B(-4,1),
C(-1,3),关于y轴对称
点的坐标分别为A’(3,5), B’(4,1),C’(1,3).依次连接A’B’,B’C’,C’A’,就得到△ABC关于y轴对称的△A’B’C’.
·
·
·
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
·
·
c
B
B’
A’
C’
[P44] 归纳: 对于这类问题,只要先求出已知图形中的一些特殊点(如多边形的顶点)的对称点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
例2:四边形ABCD的四个顶点的坐标分别是
A(-5,1), B(-2,1),
C(-2,5), D(-5,4),
分别作出与四边形ABCD关于y轴和x轴对称的图形.
x
y
0
A
B
C
D
A′
B′
C′
D′
对于这类问题,只要先求出已知图形
中的一些特殊点的对称点的坐标,
描出并连结这些点,就可以得到这
个图形的轴对称图形.
1、完成下表. [P44]
已知点 (-2,6) (1,-2) (-1,3) (-4,-2) (1,0)
关于x轴的对称点
关于y轴的对称点
(2,6)
(-2,-6)
(1,-2)
(-1,-2)
(1,3)
(-1,-3)
(4,-2)
(-4,2)
(-1,0)
(1,0)
2、已知点P(2a+b,-3a)与点P’(8,b+2).
若点p与点p’关于x轴对称,则a=_____ b=_______.
若点p与点p’关于y轴对称,则a=_____ b=_______.
练 习
2
4
6
-20
[练习]: P45:2,3。
(1,2)
·
·
·
·
·
·
[P46:7]如图,小球起始时位于(3,0),沿所示的方向击球,小球运动轨迹如图所示,用坐标描述这个运动,找出小球运动的轨迹上关于直线l对称的点.如果小球起始时位于(1,0)处,仍按原来的方向击球,请你画出这时小球运动的轨迹.
o
1
2
3
4
5
6
7
8
1
2
3
4
l
探究3:如图,分别作出点P,M,N关于直线x=1的对称点, 你能发现它们坐标之间分别有什么关系吗
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x=1
·
·
·
·
·
·
P(-2,3)
M(-1,1)
N’(5,-2)
N(-3,-2)
M’(3,1)
P’(4,3)
思考:
1、在平面直角坐标系中,点(x,y)关于直线x=1对称点的坐标是多少
2、在平面直角坐标系中,点(x, y)关于直线x=-1对称点的坐标是多少
3、在平面直角坐标系中,点(x,y)关于直线y=1对称点的坐标是多少
4、在平面直角坐标系中,点(x,y)关于直线y=-1对称点的坐标是多少
(-x+2,y)
(-x-2,y)
(x,-y+2)
(x,-y-2)
类似: 若两点(x1,y1)、(x2,y2)关于
直线y=n对称,则 ,n=
归纳: 若两点(x1,y1)、(x2,y2)关于
直线x=m对称,则m= , .
y1=y2
x1=x2
小组合作交流
点(a,b)关于直线x=m对称的点坐标为多少?
点(a,b)关于直线y=n对称的点坐标为多少?
1、学习了在平面直角坐标系中,关于x轴和y轴对称的点的坐标的特点。
这节课你学到了什么?
关于x轴对称的点横坐标相等,纵坐标互为相反数.关于y轴对称的点横坐标互为相反数,纵坐标相等.
2、学习了在平面直角坐标系中如何画一个图形关于x轴或y轴的对称图形
先求出已知图形中的一些特殊点(如多边形的顶点)的对应点的坐标,描出并连接这些点,就可以得到这个图形的轴对称图形.
作业:
完成P45第2-4题 。
谢谢指导!再见!
⒈ 快速口答
(3,6)(-7,9)关于x轴的对称点;
(-3,-5)(0,10)关于y轴的对称点.
2.根据下列点的坐标的变化,判断它们进
行了怎样的变换:
⑴(-1,3) (-1,-3)
⑵(-5,-4) (-5,4)
⑶(3,4) (-3,4)
⑷(1,0) (-1,0)
3、 如图所示的点A 、B、 C、 D 、E中,哪两个点关于x轴对称 哪两个点关于y轴对称
x
y
A
B
C
D
E
课堂检测
1、点(1,2)关于x轴的对称点是 —————,关于y轴的对称点是________.
2、点(-3,4)关于直线x=2的对称点是____.
3、已知点(x,4-y)与点(1-y,2x)关于y轴对称,则xy= ————————。
4、已知点M(3,y)在直线y= -x+1上,则点M关于x轴的对称点是__________.
7.已知点D在△ABC的边AB的垂直平分线上,且AD+DC=AC,若AC=5cm,BC=4cm,则△BDC的周长为( )
A、6cm B、7cm
C、8cm D、9cm
8.线段AB外有两点C,D(在AB同侧)使CA=CB,DA=DB,∠ADB=80°, ∠CAD=10°,则∠ACB=( )
A.90° B.100° C.110° D.120°
9.BD为CE的中垂线,A在CB延长线上,∠C=34°,则∠ABE=( )
A.17° B.34° C.68° D.136°
10. P在 AOB内;点M,N分别是点P关于AO,BO的对称点,且与AO、BO相交点E、F,若PEF的周长为15,求MN的长.
11.在由小正方形组成的L形的图中,用三种不同方法添画一个小正方形,使它成为轴对称图形。
12.在Rt△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD∶∠BAC=1∶3,求∠B的度数。
13.已知:在△ABC中,AB<AC,BC边上的垂直平分DE交BC于点D,交AC于点E,AC=8cm,△ABE的周长是14cm,求AB的长。
