2020-2021学年冀教版数学七年级下册9.2三角形的内角和外角课后培优(Word版含答案)
文档属性
| 名称 | 2020-2021学年冀教版数学七年级下册9.2三角形的内角和外角课后培优(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 607.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 00:00:00 | ||
图片预览



文档简介
9.2三角形的内角和外角
一、单选题
1.如图摆放一副三角尺,,点在上,点在的延长线上,,,,则(
)
A.
B.
C.
D.
2.下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A=∠B=∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
3.如图,在中,是的一个外角,,,则为(
)
A.
B.
C.
D.
4.光线a照射到平面镜上,然后在平面镜和之间来回反射.若已知,则(
)
A.
B.
C.
D.
5.已知直线∥,将一块含30°的直角三角尺按如图方式放置(∠ABC=60°),其中A、C两点分别落在直线、上,若∠1=20°,则∠2的度数为(
)
A.50°
B.30°
C.20°
D.40°
6.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为(
)
A.32°
B.30°
C.28°
D.26°
7.如图,,点在上,,,则下列结论正确的个数是(
)
(1);(2);(3);(4)
A.1个
B.2个
C.3个
D.4个
8.如图,在ABC中,∠B+∠C=α,按图进行翻折,使,则∠FE的度数是( )
A.
B.90°﹣
C.α﹣90°
D.2α﹣180°
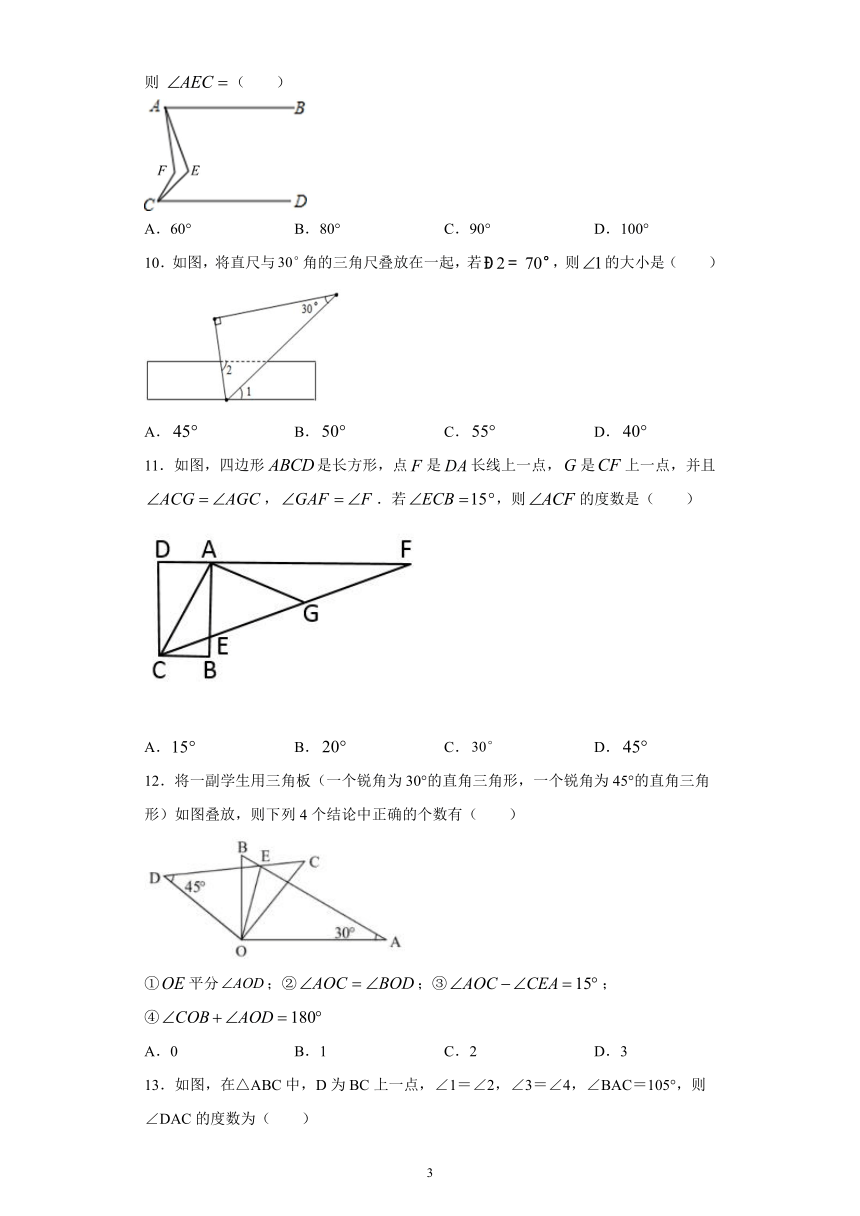
9.如图,已知,,,,则(
)
A.60°
B.80°
C.90°
D.100°
10.如图,将直尺与角的三角尺叠放在一起,若,则的大小是(
)
A.
B.
C.
D.
11.如图,四边形是长方形,点是长线上一点,是上一点,并且,.若,则的度数是(
)
A.
B.
C.
D.
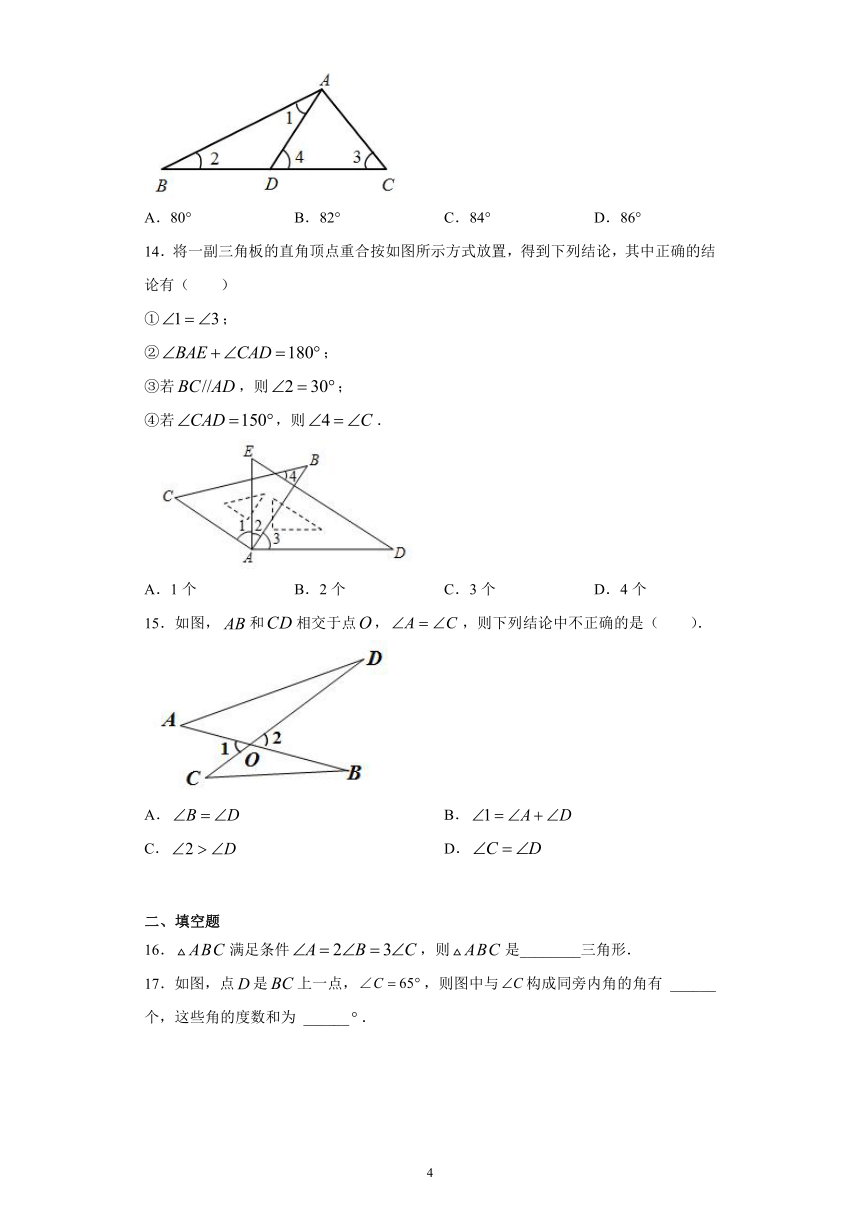
12.将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有(
)
①平分;②;③;④
A.0
B.1
C.2
D.3
13.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为(
)
A.80°
B.82°
C.84°
D.86°
14.将一副三角板的直角顶点重合按如图所示方式放置,得到下列结论,其中正确的结论有(
)
①;
②;
③若,则;
④若,则.
A.1个
B.2个
C.3个
D.4个
15.如图,和相交于点,,则下列结论中不正确的是(
).
A.
B.
C.
D.
二、填空题
16.满足条件,则是________三角形.
17.如图,点是上一点,,则图中与构成同旁内角的角有
______
个,这些角的度数和为
______.
18.在一个三角形中,如果一个内角是另一内角的倍(为整数),那么我们称这个三角形为倍三角形.如果一个三角形既是2倍角三角形,又是3倍角三角形,那么这个三角形最小的内角度数为________.
19.如图,将Rt△ABC绕点A逆时针旋转70°得到Rt△AB1C1,若,,则______.
20.如图,将一副三角尺按如图所示的方式叠放(两条直角边重合),则的度数是_____.
三、解答题
21.在证明“三角形内角和等于180”这一命题时,小彬的思路如下.请写出“求证”部分,补充第一步推理的依据并按他的思路完成后续证明.
已知:如图,.
求证:_____________________.
证明:如图,在边上取点,过点作交于点,过点作交于点.
∵,
∴,(依据:_____________________).
∵,
∴.
22.如图,点、、、都在同一直线上,与的延长线交于点,,,求证:.
23.如图,已知∠C=54°,∠E=30°,∠BDF=130°,求∠A的度数.
24.将一副直角三角尺和如图放置,其中,,,若,试判断与的位置关系,并说明理由.
25.如图,在中,于点,
交于点,于点,交
于点.
(1)求证:;
(2)若,,求
的度数.
参考答案
1.A
解:∵∠EDF=90°,∠F=45°,
∴∠DEF=45°,
∵∠B=90°,∠A=30°,
∴∠ACB=60°,
∵EF∥BC,
∴∠CEF=∠ACB=60°,
∴∠CED=∠CEF?∠DEF=15°.
2.D
解:A、在△ABC中,因为∠A:∠B:∠C=2:2:4,所以∠C=90°,∠A=∠B=45°,△ABC为直角三角形,本选项不符合题意.
B、在△ABC中,因为∠A=∠B﹣∠C,所以∠B=90°,△ABC为直角三角形,本选项不符合题意.
C、在△ABC中,因为∠A=∠B=∠C,所以∠C=90°,∠B=60°,∠A=30°,△ABC为直角三角形,本选项不符合题意.
D、在△ABC中,因为∠A=∠B=2∠C,所以∠A=∠B=72°,∠C=36°,△ABC不是直角三角形,本选项符合题意,
3.B
解:∵∠1+∠E=∠2,
∴∠E=∠2-∠1,
∵∠A+3∠1=∠ACD=3∠2,
∴∠A=3∠2-3∠1=3(∠2-∠1)=3∠E=78°,
∴∠E=26°.
4.D
解:∵∠6=∠1=55°,∠5=∠3=75°,
∴∠2=(55+75)÷2=65°,
5.D
解:∵∠ABC=60°,∠ACB=90°,
∴∠BAC=30°,
又∵a∥b,
∴∠2=180°-30°-90°-20°=40°,
6.C
解:如图,由翻折的性质得,
∴,
∴在△ADE中,,
∵,
∴,
∴,
∵,,
∴.
7.B
解:∵AB∥CD,
∴∠A+∠C=180°,
又∵∠A=110°,
∴∠C=70°,
∴∠AED=∠C+∠D=85°,故(2)正确,
∵∠C+∠D+∠CED=180°,
∴∠D+∠CED=110°,
∴∠A=∠CED+∠D,故(3)正确,
∵点E在AC上的任意一点,
∴AE无法判断等于CE,∠BED无法判断等于45°,故(1)、(4)错误,
8.D
解:设∠ADB′=γ,∠AGC′=β,∠CEB′=y,∠C′FE=x,
∵,
∴,,
∴γ+β=∠B+∠C=α,
∵EB′∥FG,
∴∠CFG=∠CEB′=y,
∴x+2y=180°①,
根据平行线的性质和翻折的性质可得:,,
∴,
∵γ+y=2∠B,
同理可得出:β+x=2∠C,
∴γ+y+β+x=2α,
∴x+y=α②,
②×2﹣①可得x=2α﹣180°,
∴∠C′FE=2α﹣180°.
9.C
解:连接AC,设∠EAF=x,∠ECF=y,
∴∠EAB=3x,∠ECD=3x,
∴∠FAB=4x,∠FCD=4x,
∵AB∥CD,
∴∠CAB+∠ACD=180°,
∵∠AFC=120°,
∴∠FAC+∠FCA=180°-120°=60°,
∴∠FAC+∠FCA+∠FAB+∠FCD=180°,即60+4x+4y=180°,
解得:x+y=30°,
∴∠AEC
=180°-(∠EAC+∠ECA)
=180°-(∠EAF+∠ECF+∠FCA+∠FAC)
=180°-(x+y+60°)
=90°
10.B
解:如图:
由题意得:∠4=180°?90°?30°=60°,
∵AB∥CD,
∴∠3=∠2=70°,
∴∠1=180°?∠3-∠4=180°?70°?60°=50°.
11.C
解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=15°,
∴∠GAF=∠F=15°,
∴∠ACF=∠AGC=∠GAF+∠F=2∠F=30°,
12.D
解:∵∠DOC=∠AOB=90°,
∴∠DOC-∠BOC=∠AOB-∠COB,
即∠AOC=∠BOD,故②正确;
∵∠AOB=∠COD=90°,
∴∠COB+∠AOD=∠AOB+∠COD=180°,故④正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC-∠CEA=15°.故③正确;
没有条件能证明OE平分∠AOD,故①错误.
综上,②③④正确,共3个,
13.A
解:∵∠BAC=105°,
∴∠2+∠3=75°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=75°,
∴∠2=25°.
∴∠DAC=105°?25°=80°.
14.C
解:
故①符合题意,
故②符合题意;
故③不符合题意;
如图,记交于
故④符合题意,
综上:符合题意的有①②④.
15.D
∵∠1=∠2,∠A=∠C,∠1=∠A+∠D,∠2=∠B+∠C,
∴∠B=∠D,
∴选项A、B正确;
∵∠2=∠A+∠D,
∴,
∴选项C正确;
没有条件说明
16.钝角
解:设∠A、∠B、∠C分别为6k、3k、2k,
则6k+3k+2k
=180°,
解得,
所以,最大的角∠A≈3×33°=99°
,
所以,这个三角形是钝角三角形.
17.4;
230.
解:由图像可知图中与构成同旁内角的角有,,,,共计4个,
由三角形的内角和定理可得:
,
,
∴
18.或或或
设最小的内角为.分类讨论:
①当2倍角为,3倍角为时,可得:,
解得.
②当2倍角为,3倍角为时,可得:,
解得.
③当3倍角为,2倍角为时,可得:,
解得.
④当即是2倍角又是三倍角时,即另一个内角为,可得:,
解得.
综上可知,最小的内角为或或或.
19.
解:∵Rt△ABC绕点A逆时针旋转70°得到Rt△AB1C1,
∴∠CAC1=70°,
∵∠C=90°,∠B=60°,
∴∠CAB=30°,
∴∠BAC1=∠CAC1-∠CAB=70°-30°=40°.
20.
解:由于是两个直角三角形,所以上下两线平行,
如图所示则,
根据三角形外角定理,
21.;两直线平行,同位角相等;见解析.
解:已知:如图,.
求证:.
证明:在边上取点,过点作交于点,过点作交于点.
∵,
∴,(依据:两直线平行,同位角相等).
∵,
∴,.
∴
∵
∴
22.见详解
解:∵
∴
∵,
,
,
∴
23.46°
解:∵∠BDF=130°,
∴∠EDF=180°﹣130°=50°.
∵∠E=30°,
∴∠AFC=30°+50°=80°.
∵∠C=54°,
∴∠A=180°﹣∠C﹣∠AFC=180°﹣54°﹣80°=46°.
24.AE与BC平行,理由见解析.
解:AE与BC平行.理由:
∵∠AFD是△AEF的外角,,,
∴∠EAF=∠AFD-∠AED=75°-45°=30°,
又∵∠BCA=30°,
∴∠EAF=∠BCA,
∴AE∥BC.
25.(1)证明见详解;(2).
(1)证明:,
,
,,
,
,
;
(2)解:,,
,
,
,
.
一、单选题
1.如图摆放一副三角尺,,点在上,点在的延长线上,,,,则(
)
A.
B.
C.
D.
2.下列说法中错误的是( )
A.在△ABC中,若∠A:∠B:∠C=2:2:4,则△ABC为直角三角形
B.在△ABC中,若∠A=∠B﹣∠C,则△ABC为直角三角形
C.在△ABC中,若∠A=∠B=∠C,则△ABC为直角三角形
D.在△ABC中,∠A=∠B=2∠C,则△ABC为直角三角形
3.如图,在中,是的一个外角,,,则为(
)
A.
B.
C.
D.
4.光线a照射到平面镜上,然后在平面镜和之间来回反射.若已知,则(
)
A.
B.
C.
D.
5.已知直线∥,将一块含30°的直角三角尺按如图方式放置(∠ABC=60°),其中A、C两点分别落在直线、上,若∠1=20°,则∠2的度数为(
)
A.50°
B.30°
C.20°
D.40°
6.如图,把纸片沿DE折叠,点A落在四边形BCED的外部,,,则的度数为(
)
A.32°
B.30°
C.28°
D.26°
7.如图,,点在上,,,则下列结论正确的个数是(
)
(1);(2);(3);(4)
A.1个
B.2个
C.3个
D.4个
8.如图,在ABC中,∠B+∠C=α,按图进行翻折,使,则∠FE的度数是( )
A.
B.90°﹣
C.α﹣90°
D.2α﹣180°
9.如图,已知,,,,则(
)
A.60°
B.80°
C.90°
D.100°
10.如图,将直尺与角的三角尺叠放在一起,若,则的大小是(
)
A.
B.
C.
D.
11.如图,四边形是长方形,点是长线上一点,是上一点,并且,.若,则的度数是(
)
A.
B.
C.
D.
12.将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有(
)
①平分;②;③;④
A.0
B.1
C.2
D.3
13.如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=105°,则∠DAC的度数为(
)
A.80°
B.82°
C.84°
D.86°
14.将一副三角板的直角顶点重合按如图所示方式放置,得到下列结论,其中正确的结论有(
)
①;
②;
③若,则;
④若,则.
A.1个
B.2个
C.3个
D.4个
15.如图,和相交于点,,则下列结论中不正确的是(
).
A.
B.
C.
D.
二、填空题
16.满足条件,则是________三角形.
17.如图,点是上一点,,则图中与构成同旁内角的角有
______
个,这些角的度数和为
______.
18.在一个三角形中,如果一个内角是另一内角的倍(为整数),那么我们称这个三角形为倍三角形.如果一个三角形既是2倍角三角形,又是3倍角三角形,那么这个三角形最小的内角度数为________.
19.如图,将Rt△ABC绕点A逆时针旋转70°得到Rt△AB1C1,若,,则______.
20.如图,将一副三角尺按如图所示的方式叠放(两条直角边重合),则的度数是_____.
三、解答题
21.在证明“三角形内角和等于180”这一命题时,小彬的思路如下.请写出“求证”部分,补充第一步推理的依据并按他的思路完成后续证明.
已知:如图,.
求证:_____________________.
证明:如图,在边上取点,过点作交于点,过点作交于点.
∵,
∴,(依据:_____________________).
∵,
∴.
22.如图,点、、、都在同一直线上,与的延长线交于点,,,求证:.
23.如图,已知∠C=54°,∠E=30°,∠BDF=130°,求∠A的度数.
24.将一副直角三角尺和如图放置,其中,,,若,试判断与的位置关系,并说明理由.
25.如图,在中,于点,
交于点,于点,交
于点.
(1)求证:;
(2)若,,求
的度数.
参考答案
1.A
解:∵∠EDF=90°,∠F=45°,
∴∠DEF=45°,
∵∠B=90°,∠A=30°,
∴∠ACB=60°,
∵EF∥BC,
∴∠CEF=∠ACB=60°,
∴∠CED=∠CEF?∠DEF=15°.
2.D
解:A、在△ABC中,因为∠A:∠B:∠C=2:2:4,所以∠C=90°,∠A=∠B=45°,△ABC为直角三角形,本选项不符合题意.
B、在△ABC中,因为∠A=∠B﹣∠C,所以∠B=90°,△ABC为直角三角形,本选项不符合题意.
C、在△ABC中,因为∠A=∠B=∠C,所以∠C=90°,∠B=60°,∠A=30°,△ABC为直角三角形,本选项不符合题意.
D、在△ABC中,因为∠A=∠B=2∠C,所以∠A=∠B=72°,∠C=36°,△ABC不是直角三角形,本选项符合题意,
3.B
解:∵∠1+∠E=∠2,
∴∠E=∠2-∠1,
∵∠A+3∠1=∠ACD=3∠2,
∴∠A=3∠2-3∠1=3(∠2-∠1)=3∠E=78°,
∴∠E=26°.
4.D
解:∵∠6=∠1=55°,∠5=∠3=75°,
∴∠2=(55+75)÷2=65°,
5.D
解:∵∠ABC=60°,∠ACB=90°,
∴∠BAC=30°,
又∵a∥b,
∴∠2=180°-30°-90°-20°=40°,
6.C
解:如图,由翻折的性质得,
∴,
∴在△ADE中,,
∵,
∴,
∴,
∵,,
∴.
7.B
解:∵AB∥CD,
∴∠A+∠C=180°,
又∵∠A=110°,
∴∠C=70°,
∴∠AED=∠C+∠D=85°,故(2)正确,
∵∠C+∠D+∠CED=180°,
∴∠D+∠CED=110°,
∴∠A=∠CED+∠D,故(3)正确,
∵点E在AC上的任意一点,
∴AE无法判断等于CE,∠BED无法判断等于45°,故(1)、(4)错误,
8.D
解:设∠ADB′=γ,∠AGC′=β,∠CEB′=y,∠C′FE=x,
∵,
∴,,
∴γ+β=∠B+∠C=α,
∵EB′∥FG,
∴∠CFG=∠CEB′=y,
∴x+2y=180°①,
根据平行线的性质和翻折的性质可得:,,
∴,
∵γ+y=2∠B,
同理可得出:β+x=2∠C,
∴γ+y+β+x=2α,
∴x+y=α②,
②×2﹣①可得x=2α﹣180°,
∴∠C′FE=2α﹣180°.
9.C
解:连接AC,设∠EAF=x,∠ECF=y,
∴∠EAB=3x,∠ECD=3x,
∴∠FAB=4x,∠FCD=4x,
∵AB∥CD,
∴∠CAB+∠ACD=180°,
∵∠AFC=120°,
∴∠FAC+∠FCA=180°-120°=60°,
∴∠FAC+∠FCA+∠FAB+∠FCD=180°,即60+4x+4y=180°,
解得:x+y=30°,
∴∠AEC
=180°-(∠EAC+∠ECA)
=180°-(∠EAF+∠ECF+∠FCA+∠FAC)
=180°-(x+y+60°)
=90°
10.B
解:如图:
由题意得:∠4=180°?90°?30°=60°,
∵AB∥CD,
∴∠3=∠2=70°,
∴∠1=180°?∠3-∠4=180°?70°?60°=50°.
11.C
解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=15°,
∴∠GAF=∠F=15°,
∴∠ACF=∠AGC=∠GAF+∠F=2∠F=30°,
12.D
解:∵∠DOC=∠AOB=90°,
∴∠DOC-∠BOC=∠AOB-∠COB,
即∠AOC=∠BOD,故②正确;
∵∠AOB=∠COD=90°,
∴∠COB+∠AOD=∠AOB+∠COD=180°,故④正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC-∠CEA=15°.故③正确;
没有条件能证明OE平分∠AOD,故①错误.
综上,②③④正确,共3个,
13.A
解:∵∠BAC=105°,
∴∠2+∠3=75°①
∵∠1=∠2,
∴∠4=∠3=∠1+∠2=2∠2②
把②代入①得:3∠2=75°,
∴∠2=25°.
∴∠DAC=105°?25°=80°.
14.C
解:
故①符合题意,
故②符合题意;
故③不符合题意;
如图,记交于
故④符合题意,
综上:符合题意的有①②④.
15.D
∵∠1=∠2,∠A=∠C,∠1=∠A+∠D,∠2=∠B+∠C,
∴∠B=∠D,
∴选项A、B正确;
∵∠2=∠A+∠D,
∴,
∴选项C正确;
没有条件说明
16.钝角
解:设∠A、∠B、∠C分别为6k、3k、2k,
则6k+3k+2k
=180°,
解得,
所以,最大的角∠A≈3×33°=99°
,
所以,这个三角形是钝角三角形.
17.4;
230.
解:由图像可知图中与构成同旁内角的角有,,,,共计4个,
由三角形的内角和定理可得:
,
,
∴
18.或或或
设最小的内角为.分类讨论:
①当2倍角为,3倍角为时,可得:,
解得.
②当2倍角为,3倍角为时,可得:,
解得.
③当3倍角为,2倍角为时,可得:,
解得.
④当即是2倍角又是三倍角时,即另一个内角为,可得:,
解得.
综上可知,最小的内角为或或或.
19.
解:∵Rt△ABC绕点A逆时针旋转70°得到Rt△AB1C1,
∴∠CAC1=70°,
∵∠C=90°,∠B=60°,
∴∠CAB=30°,
∴∠BAC1=∠CAC1-∠CAB=70°-30°=40°.
20.
解:由于是两个直角三角形,所以上下两线平行,
如图所示则,
根据三角形外角定理,
21.;两直线平行,同位角相等;见解析.
解:已知:如图,.
求证:.
证明:在边上取点,过点作交于点,过点作交于点.
∵,
∴,(依据:两直线平行,同位角相等).
∵,
∴,.
∴
∵
∴
22.见详解
解:∵
∴
∵,
,
,
∴
23.46°
解:∵∠BDF=130°,
∴∠EDF=180°﹣130°=50°.
∵∠E=30°,
∴∠AFC=30°+50°=80°.
∵∠C=54°,
∴∠A=180°﹣∠C﹣∠AFC=180°﹣54°﹣80°=46°.
24.AE与BC平行,理由见解析.
解:AE与BC平行.理由:
∵∠AFD是△AEF的外角,,,
∴∠EAF=∠AFD-∠AED=75°-45°=30°,
又∵∠BCA=30°,
∴∠EAF=∠BCA,
∴AE∥BC.
25.(1)证明见详解;(2).
(1)证明:,
,
,,
,
,
;
(2)解:,,
,
,
,
.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
