19.2.1矩形的定义及性质
文档属性
| 名称 | 19.2.1矩形的定义及性质 |  | |
| 格式 | zip | ||
| 文件大小 | 527.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-07 07:42:16 | ||
图片预览


文档简介
(共28张PPT)
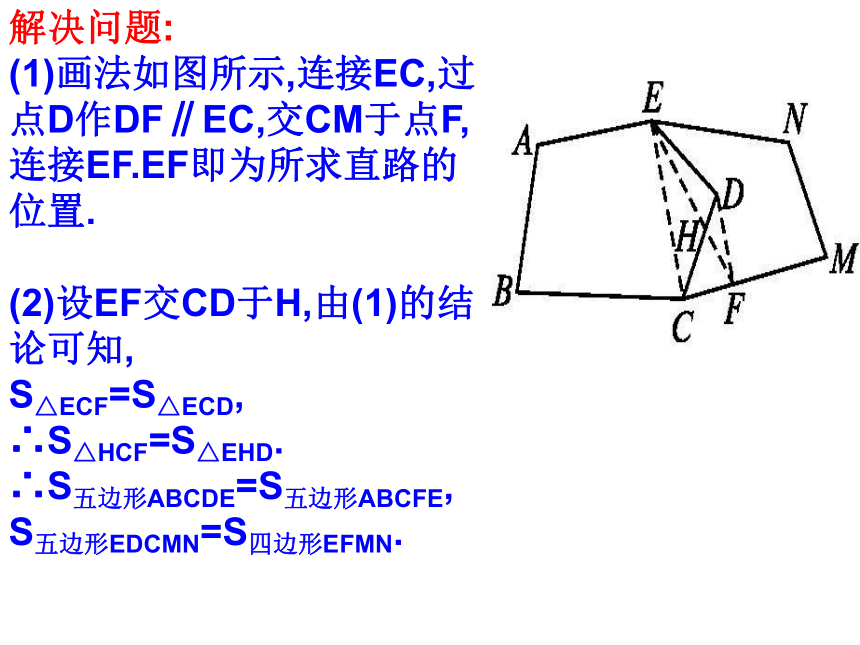
10、 田村有一口呈四边形的池塘,在它 的四个角A、B、C、D处均种有一棵大核桃树.田村准备开挖鱼池建养鱼苗,想使池塘面积扩大一倍,又想保持 核桃树不动,并要求扩建后的池塘成平行四边形形状, 请问田村能否实现这一设想 若能,请你设计并画出图形;若不能,请说明理由.
O
A
B
C
D
E
F
G
H
解决问题:
(1)画法如图所示,连接EC,过点D作DF∥EC,交CM于点F,连接EF.EF即为所求直路的位置.
(2)设EF交CD于H,由(1)的结论可知,
S△ECF=S△ECD,
∴S△HCF=S△EHD.
∴S五边形ABCDE=S五边形ABCFE,
S五边形EDCMN=S四边形EFMN.
19.2.1特殊的平行四边形
(矩形的定义及性质)
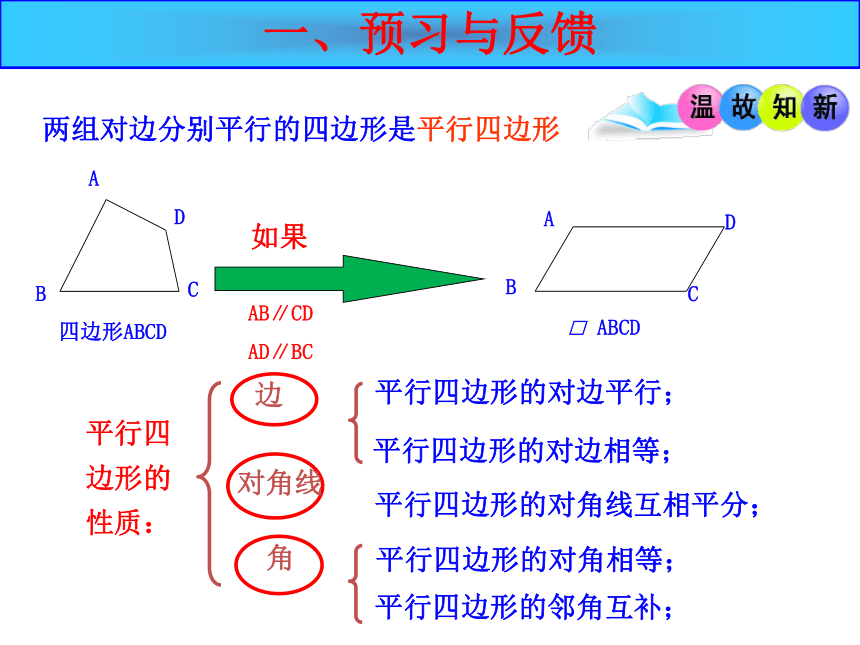
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
□ ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
一、预习与反馈
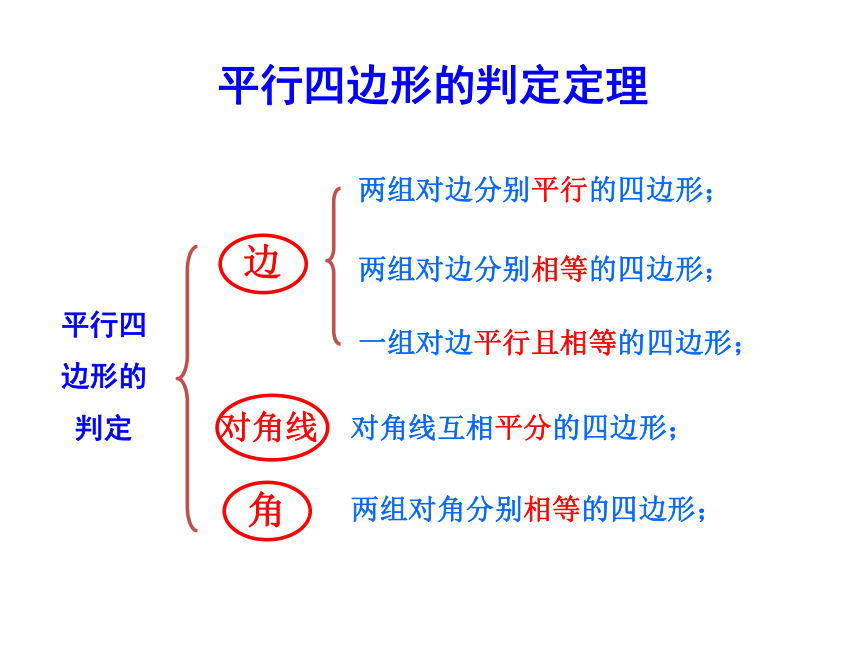
平行四边形的判定
边
两组对边分别平行的四边形;
两组对边分别相等的四边形;
角
两组对角分别相等的四边形;
对角线
对角线互相平分的四边形;
一组对边平行且相等的四边形;
平行四边形的判定定理
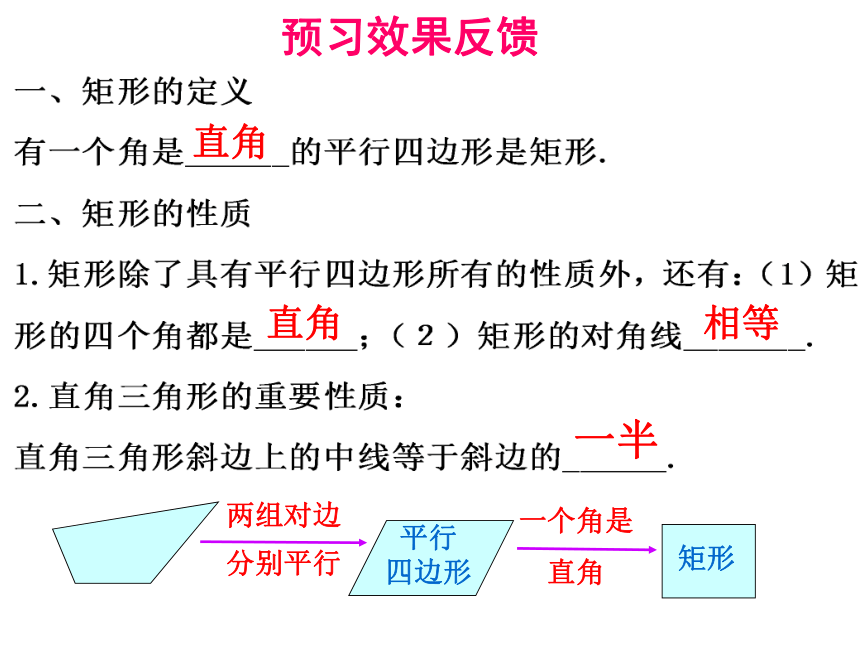
直角
一半
相等
直角
预习效果反馈
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
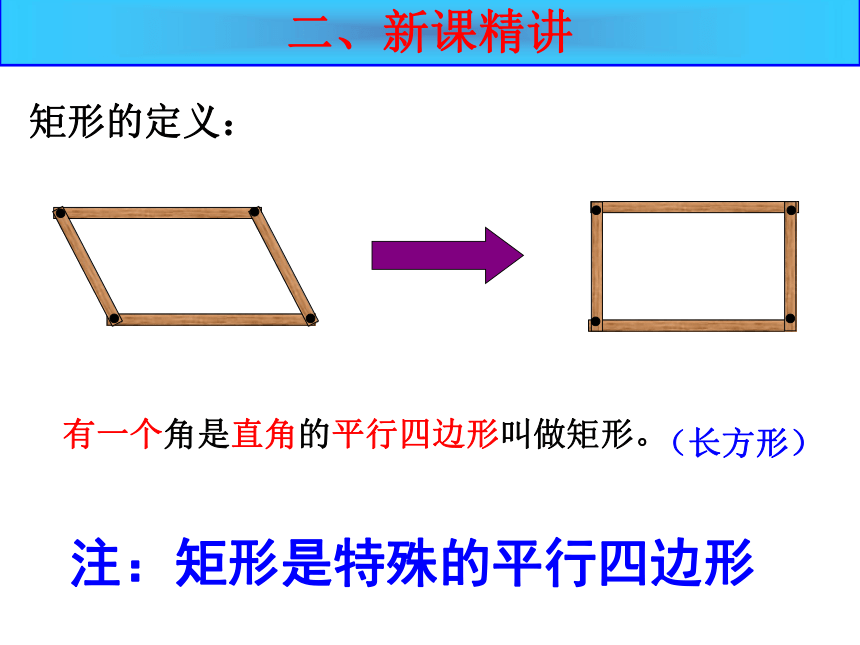
有一个角是直角的平行四边形叫做矩形。
(长方形)
矩形的定义:
二、新课精讲
注:矩形是特殊的平行四边形
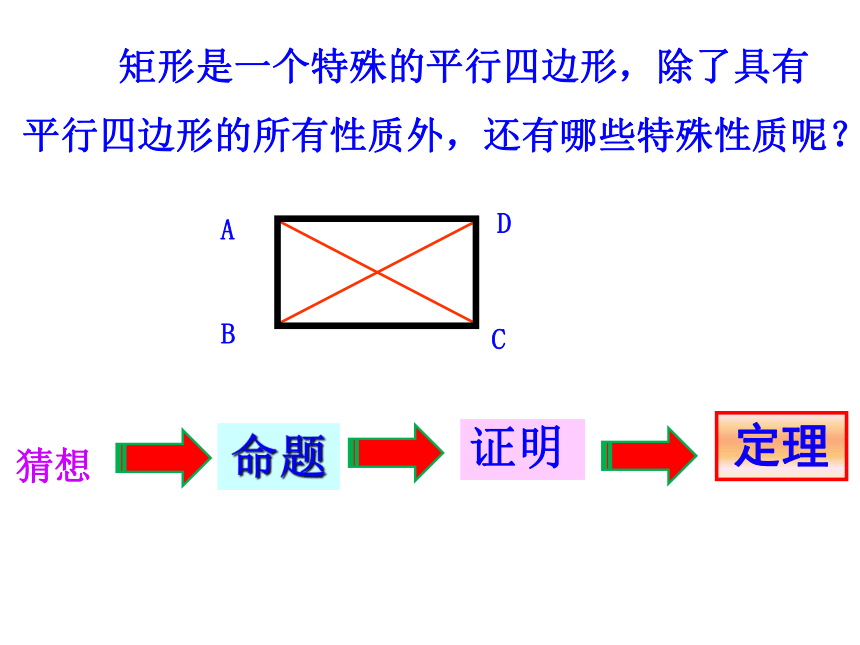
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想
A
B
C
D
命题
证明
定理
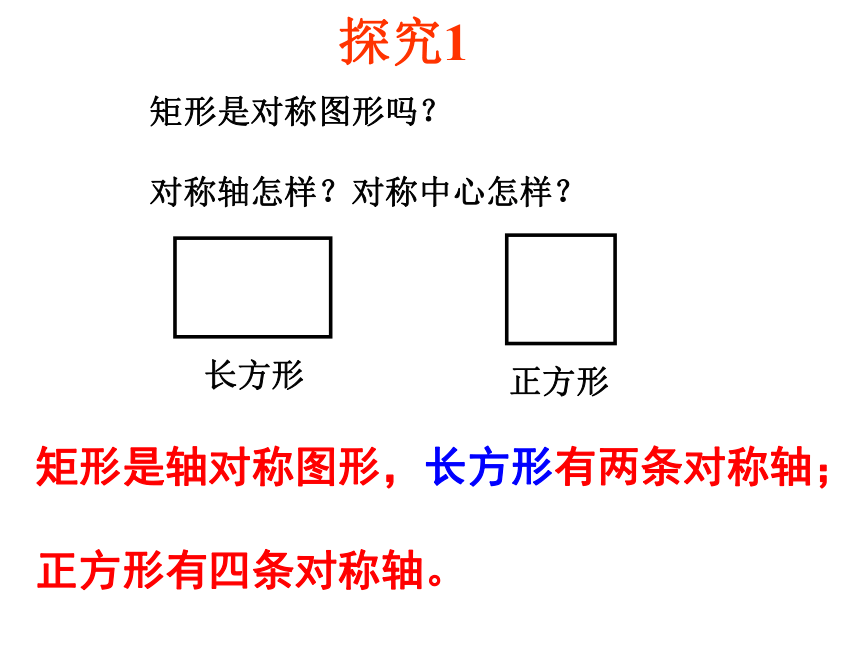
探究1
矩形是对称图形吗?
对称轴怎样?对称中心怎样?
长方形
正方形
矩形是轴对称图形,长方形有两条对称轴;
正方形有四条对称轴。
探究2
如图,当□ABCD的一个角变为直角,我们知道,此时,四边形变为一个矩形。其它三个角又将会是什么样的角呢?
矩形的四个角都是直角。
猜想:
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:∵四边形ABCD是矩形
∴ ∠A=90°
又∵矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
矩形的四个角都相等,
都是900。
矩形的性质1:
探究3
如图,当□ABCD的一个角变为直角,我们知道,此时,四边形变为一个矩形。它的两条对角线有什么关系?
猜测:
矩形的两条对角线相等。
已知:如图,矩形ABCD的对角线AC、BD相交于点O。
求证:AC=BD。
证一证
D
A
B
C
O
矩形的对角线相等。
矩形的性质2:
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
探究4
矩形的两条对角线相等且互相平分,变形为直角三角形,你有什么发现?
D
A
B
C
O
OC= BD
归纳
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半。
A
B
C
D
∵∠ABC=90 °
∴□ABCD是矩形
O
C
B
A
D
证明: 延长BO至D,使OD=BO, 连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∴AC=BD
∴BO= BD= AC
已知:在Rt△ABC中,∠ABC=90 °,BO是AC上的中线.
求证: BO = AC
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD ∥BC ,CD ∥AB
∴AC= BD
A
B
C
D
O
∴AO= CO ,OD = OB
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长.
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4㎝
∴ 矩形的对角线长 AC=BD=2OA=8㎝
解:∵ 四边形ABCD是矩形
D
C
B
A
o
练一练
1.如图,四边形ABCD是矩形,找出图中相等的线段和相等的角。
D
A
B
C
O
相等的线段:
AB=CD AD=BC AC=BD
OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
O
D
C
B
A
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
P95练习3:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8cm,求矩形对角线的长.
A
B
O
C
D
解:
在矩形ABCD中,
∵ ∠AOD=120°
∴ ∠AOB=60°
∵OA=OB
∴ △AOB为等边三角形
∴AB=OA= AC=4cm
在Rt△ABC中,
≈6.93(cm)
BC=
=
=
方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形.
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形、轴对称图形
O
这是矩形所特有的性质
比一比 知关系
1.如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为( )
A.4 B .3 C .2 D.1
D
A
B
C
O
2.已知矩形的一条对角线与一边的夹角是40° ,则两条对角线所成锐角的度数为( )
A.50 ° B.60 ° C.70 ° D.80 °
D
A
B
C
O
三、反馈练习
3.直角三角形中,两直角边分别是12和5,则斜边上的中线长是( )
A.34 B.26 C.8.5 D.6.5
A
B
C
D
4、下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
D
5. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于( )
A.30° B.45° C.60° D.120°
A
D
C
B
A
┓
6.已知△ABC是直角三角形,∠ABC=90°,BD是斜边AC上的中线
(1)若BD=3㎝,则AC= _______ ㎝
(2)若∠C=30°,AB=5㎝,则AC=_______㎝,
BD=_______㎝.
6
5
10
四、小结测试
1.(2011·四川绵阳中考)下列关于矩形的说法中正确的是( ).
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分
D.矩形的对角线相等且互相平分
D
2.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要 添加的条件是 ( ).
A.AB=CD B.AD=BC
C.AB=BC D.AC=BD
D
3.(2011·浙江温州中考)如图,在矩形ABCD中,对角线AC,BD交于 点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有( ).
A.2条 B.4条 C.5条 D.6条
解析:
由矩形ABCD得OA=OB=OC=OD.
由∠AOB=60°,得OA=OB=AB=OC=OD=DC=8.
共有6条线段长度等于8.
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO, AD的中点,若AC=8,则EF= .
解析:
根据矩形的对角线相等且互相平分得OD=4,
再根据三角形的中位线的性质得
EF= OD=2.
5.求证:矩形的对角线相等.
已知:如图四边形ABCD是矩形,AC与BD是对角线.
求证:AC=BD.
证明:
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°.
又∵BC=CB,
∴△ABC≌△DCB.
∴AC=BD,
∴矩形的对角线相等.
6.如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.
(1)求∠2的度数;
(2)求证:BO=BE.
(1)解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°.
∵AE平分∠BAD,∴∠BAE=∠DAE=45°.
∴∠AEB=90°-45°=45°,∠2=45°-∠1=30°.
∴OA=OB.∵∠2=30°,∠ABC=90°,
∴∠BAO=60°.∴△ABO是等边三角形.
∴OB=AB.又∵∠BAE=∠AEB=45°,
∴BE=AB.∴BO=BE.
(2)证明:∵四边形ABCD是矩形,
∴AC=BD,OA= AC,OB= BD,
10、 田村有一口呈四边形的池塘,在它 的四个角A、B、C、D处均种有一棵大核桃树.田村准备开挖鱼池建养鱼苗,想使池塘面积扩大一倍,又想保持 核桃树不动,并要求扩建后的池塘成平行四边形形状, 请问田村能否实现这一设想 若能,请你设计并画出图形;若不能,请说明理由.
O
A
B
C
D
E
F
G
H
解决问题:
(1)画法如图所示,连接EC,过点D作DF∥EC,交CM于点F,连接EF.EF即为所求直路的位置.
(2)设EF交CD于H,由(1)的结论可知,
S△ECF=S△ECD,
∴S△HCF=S△EHD.
∴S五边形ABCDE=S五边形ABCFE,
S五边形EDCMN=S四边形EFMN.
19.2.1特殊的平行四边形
(矩形的定义及性质)
两组对边分别平行的四边形是平行四边形
A
B
C
D
四边形ABCD
如果
AB∥CD
AD∥BC
B
D
□ ABCD
A
C
平行四边形的性质:
边
平行四边形的对边平行;
平行四边形的对边相等;
角
平行四边形的对角相等;
平行四边形的邻角互补;
对角线
平行四边形的对角线互相平分;
一、预习与反馈
平行四边形的判定
边
两组对边分别平行的四边形;
两组对边分别相等的四边形;
角
两组对角分别相等的四边形;
对角线
对角线互相平分的四边形;
一组对边平行且相等的四边形;
平行四边形的判定定理
直角
一半
相等
直角
预习效果反馈
一个角是
直角
两组对边
分别平行
平行
四边形
矩形
有一个角是直角的平行四边形叫做矩形。
(长方形)
矩形的定义:
二、新课精讲
注:矩形是特殊的平行四边形
矩形是一个特殊的平行四边形,除了具有平行四边形的所有性质外,还有哪些特殊性质呢?
猜想
A
B
C
D
命题
证明
定理
探究1
矩形是对称图形吗?
对称轴怎样?对称中心怎样?
长方形
正方形
矩形是轴对称图形,长方形有两条对称轴;
正方形有四条对称轴。
探究2
如图,当□ABCD的一个角变为直角,我们知道,此时,四边形变为一个矩形。其它三个角又将会是什么样的角呢?
矩形的四个角都是直角。
猜想:
已知:如图,四边形ABCD是矩形
求证:∠A=∠B=∠C=∠D=90°
A
B
C
D
证明:∵四边形ABCD是矩形
∴ ∠A=90°
又∵矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B = 180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
矩形的四个角都相等,
都是900。
矩形的性质1:
探究3
如图,当□ABCD的一个角变为直角,我们知道,此时,四边形变为一个矩形。它的两条对角线有什么关系?
猜测:
矩形的两条对角线相等。
已知:如图,矩形ABCD的对角线AC、BD相交于点O。
求证:AC=BD。
证一证
D
A
B
C
O
矩形的对角线相等。
矩形的性质2:
证明:在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC , BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
探究4
矩形的两条对角线相等且互相平分,变形为直角三角形,你有什么发现?
D
A
B
C
O
OC= BD
归纳
直角三角形的性质:
直角三角形斜边上的中线等于斜边的一半。
A
B
C
D
∵∠ABC=90 °
∴□ABCD是矩形
O
C
B
A
D
证明: 延长BO至D,使OD=BO, 连结AD、DC.
∵AO=OC, BO=OD
∴四边形ABCD是平行四边形.
∴AC=BD
∴BO= BD= AC
已知:在Rt△ABC中,∠ABC=90 °,BO是AC上的中线.
求证: BO = AC
矩形的 两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形 的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD = BC ,CD = AB
∴AD ∥BC ,CD ∥AB
∴AC= BD
A
B
C
D
O
∴AO= CO ,OD = OB
例1: 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4㎝,求矩形对角线的长.
∴AC与BD相等且互相平分
∴ OA=OB
∵ ∠AOB=60°
∴ △AOB是等边三角形
∴ OA=AB=4㎝
∴ 矩形的对角线长 AC=BD=2OA=8㎝
解:∵ 四边形ABCD是矩形
D
C
B
A
o
练一练
1.如图,四边形ABCD是矩形,找出图中相等的线段和相等的角。
D
A
B
C
O
相等的线段:
AB=CD AD=BC AC=BD
OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
O
D
C
B
A
相等的线段:
AB=CD AD=BC AC=BD OA=OC=OB=OD= AC= BD
相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB
等腰三角形有:
△OAB △ OBC △OCD △OAD
直角三角形有:
Rt△ABC Rt△BCD Rt△CDA Rt△DAB
全等三角形有:
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
△OAB≌△OCD △OAD≌△OCB
已知四边形ABCD是矩形
P95练习3:已知:如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AC=8cm,求矩形对角线的长.
A
B
O
C
D
解:
在矩形ABCD中,
∵ ∠AOD=120°
∴ ∠AOB=60°
∵OA=OB
∴ △AOB为等边三角形
∴AB=OA= AC=4cm
在Rt△ABC中,
≈6.93(cm)
BC=
=
=
方法小结: 如果矩形两对角 线的夹角是60°
或120°, 则其中必有等边三角形.
边 角 对角线 对称性
平行四
边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形、轴对称图形
O
这是矩形所特有的性质
比一比 知关系
1.如图,在矩形ABCD中,对角线AC、BD相交于点O,若OA=2,则BD的长为( )
A.4 B .3 C .2 D.1
D
A
B
C
O
2.已知矩形的一条对角线与一边的夹角是40° ,则两条对角线所成锐角的度数为( )
A.50 ° B.60 ° C.70 ° D.80 °
D
A
B
C
O
三、反馈练习
3.直角三角形中,两直角边分别是12和5,则斜边上的中线长是( )
A.34 B.26 C.8.5 D.6.5
A
B
C
D
4、下面性质中,矩形不一定具有的是( )
A.对角线相等 B.四个角都相等
C.是轴对称图形 D.对角线垂直
D
5. 矩形ABCD中,AB=2BC,E在CD上,AE=AB,则∠BAE等于( )
A.30° B.45° C.60° D.120°
A
D
C
B
A
┓
6.已知△ABC是直角三角形,∠ABC=90°,BD是斜边AC上的中线
(1)若BD=3㎝,则AC= _______ ㎝
(2)若∠C=30°,AB=5㎝,则AC=_______㎝,
BD=_______㎝.
6
5
10
四、小结测试
1.(2011·四川绵阳中考)下列关于矩形的说法中正确的是( ).
A.对角线相等的四边形是矩形
B.对角线互相平分的四边形是矩形
C.矩形的对角线互相垂直且平分
D.矩形的对角线相等且互相平分
D
2.如图,四边形ABCD的对角线互相平分,要使它成为矩形,那么需要 添加的条件是 ( ).
A.AB=CD B.AD=BC
C.AB=BC D.AC=BD
D
3.(2011·浙江温州中考)如图,在矩形ABCD中,对角线AC,BD交于 点O.已知∠AOB=60°,AC=16,则图中长度为8的线段有( ).
A.2条 B.4条 C.5条 D.6条
解析:
由矩形ABCD得OA=OB=OC=OD.
由∠AOB=60°,得OA=OB=AB=OC=OD=DC=8.
共有6条线段长度等于8.
4.如图,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO, AD的中点,若AC=8,则EF= .
解析:
根据矩形的对角线相等且互相平分得OD=4,
再根据三角形的中位线的性质得
EF= OD=2.
5.求证:矩形的对角线相等.
已知:如图四边形ABCD是矩形,AC与BD是对角线.
求证:AC=BD.
证明:
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°.
又∵BC=CB,
∴△ABC≌△DCB.
∴AC=BD,
∴矩形的对角线相等.
6.如图,在矩形ABCD中,AE平分∠BAD,∠1=15°.
(1)求∠2的度数;
(2)求证:BO=BE.
(1)解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=90°.
∵AE平分∠BAD,∴∠BAE=∠DAE=45°.
∴∠AEB=90°-45°=45°,∠2=45°-∠1=30°.
∴OA=OB.∵∠2=30°,∠ABC=90°,
∴∠BAO=60°.∴△ABO是等边三角形.
∴OB=AB.又∵∠BAE=∠AEB=45°,
∴BE=AB.∴BO=BE.
(2)证明:∵四边形ABCD是矩形,
∴AC=BD,OA= AC,OB= BD,
