19.2.2_菱形的定义及性质
文档属性
| 名称 | 19.2.2_菱形的定义及性质 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-07 00:00:00 | ||
图片预览




文档简介
(共31张PPT)
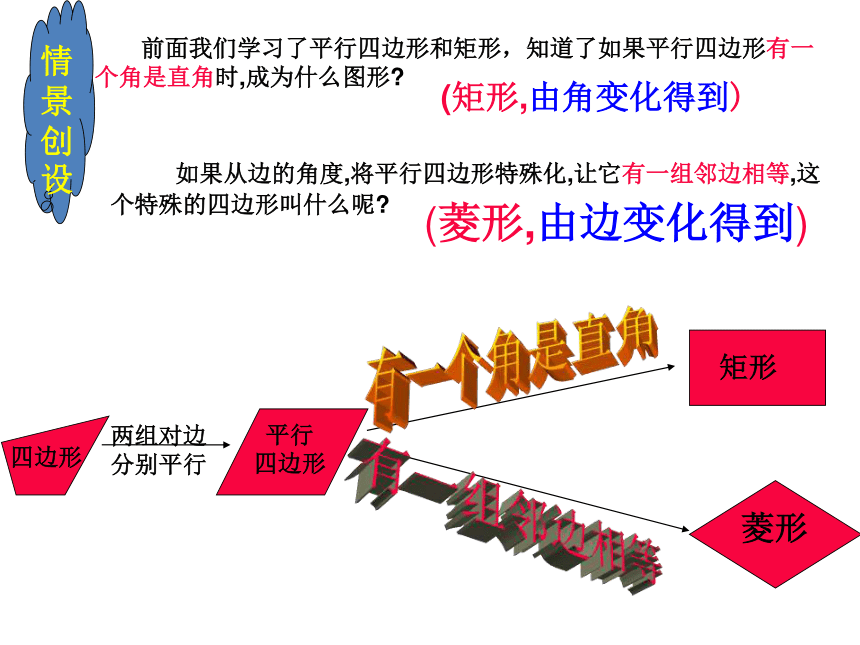
3.如图(1),在矩形ABCD中,动点P从点B出发,
沿BC,CD,DA运动至点A停止,设点P运动的路程为x,
△ABP的面积为y,如果y关于x的函数图象如图(2)所示,
则矩形ABCD的面积是( ).
A.10 B.16 C.20 D.36
解析:由图可知,BC=4,CD=9-4=5,则矩形ABCD的面积是20.
答案:C
8.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的
延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
(1)证明:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,
∴EB=EC.
∴△ABE≌△FCE.
∴AB=CF.
(2)解:当BC=AF时,四边形ABFC是矩形.
理由如下:
∵AB∥CF,AB=CF,
∴四边形ABFC是平行四边形.
∵BC=AF,
∴四边形ABFC是矩形.
19.2.2 菱形
A
B
C
D
O
地调学校数学教研组
1.矩形的性质:(1)矩形的四个角都是____;(2)矩形的对角线____.
学 前 温 故
2.矩形的判定:(1)有一个角是直角的__________是矩形;(2)对角线_______的平行四边形是矩形.
直角
相等
平行四边形
相
等
一、预习与反馈
1.菱形的概念
有一组邻边 的平行四边形叫做菱形.
相等
新 课 早 知
2.菱形的性质
菱形的四条边都 ;菱形的两条对角线 ,并且每 一条对角线平分一组 .
对角
相等
互相垂直
两组对边
分别平行
平行
四边形
矩形
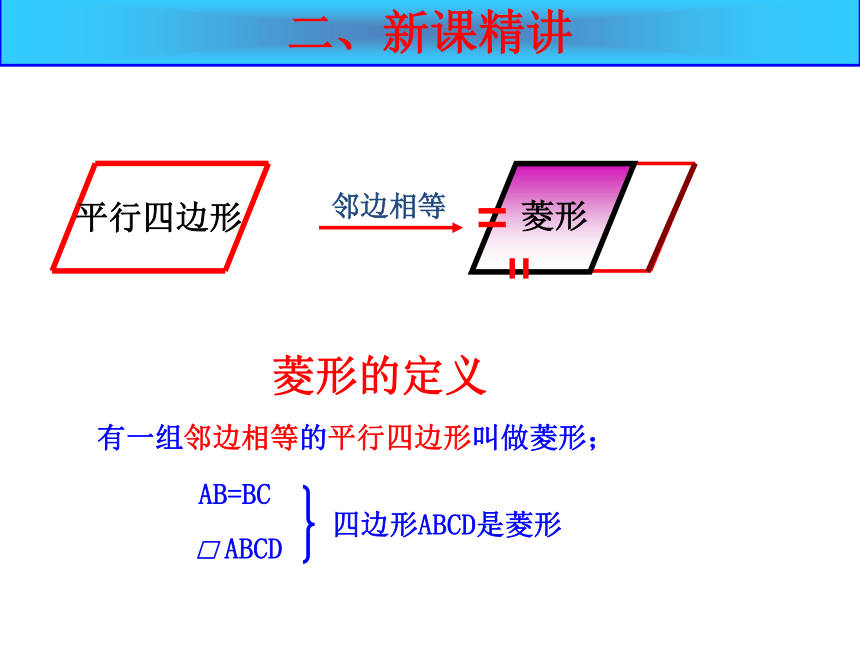
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形
菱形
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢
(菱形,由边变化得到)
四边形
情景创设
平行四边形
菱形
邻边相等
二、新课精讲
有一组邻边相等的平行四边形叫做菱形;
AB=BC
四边形ABCD是菱形
□ ABCD
菱形的定义
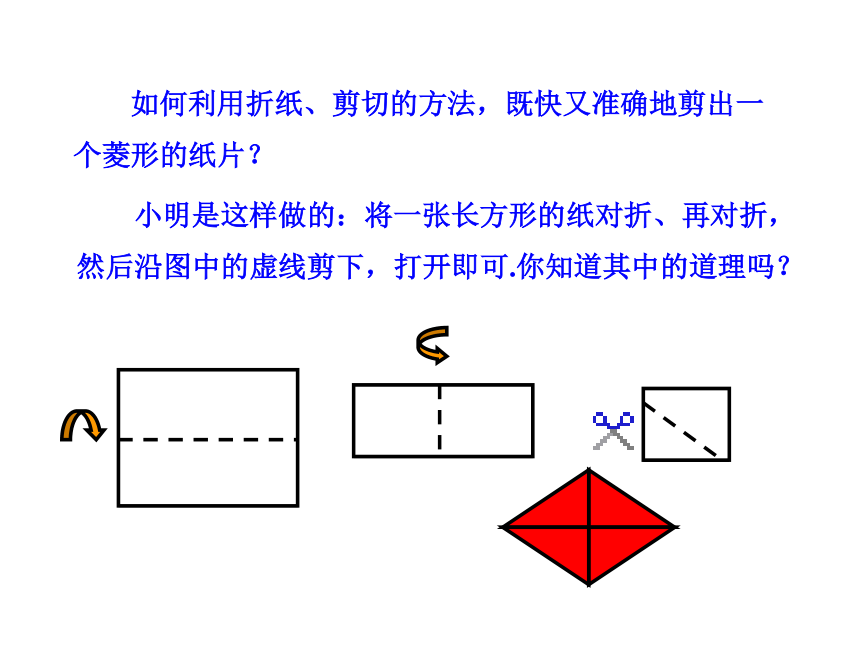
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
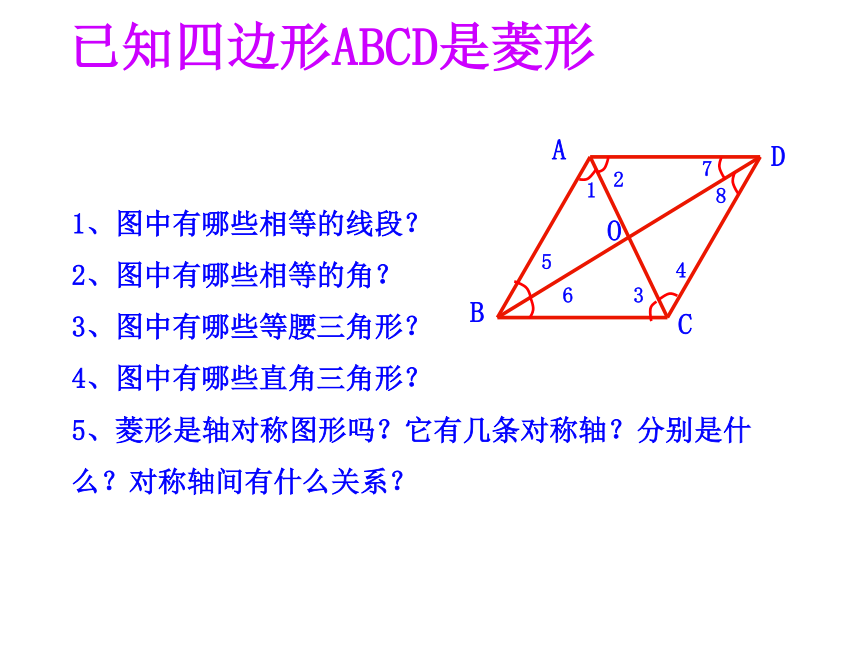
1、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些等腰三角形?
4、图中有哪些直角三角形?
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
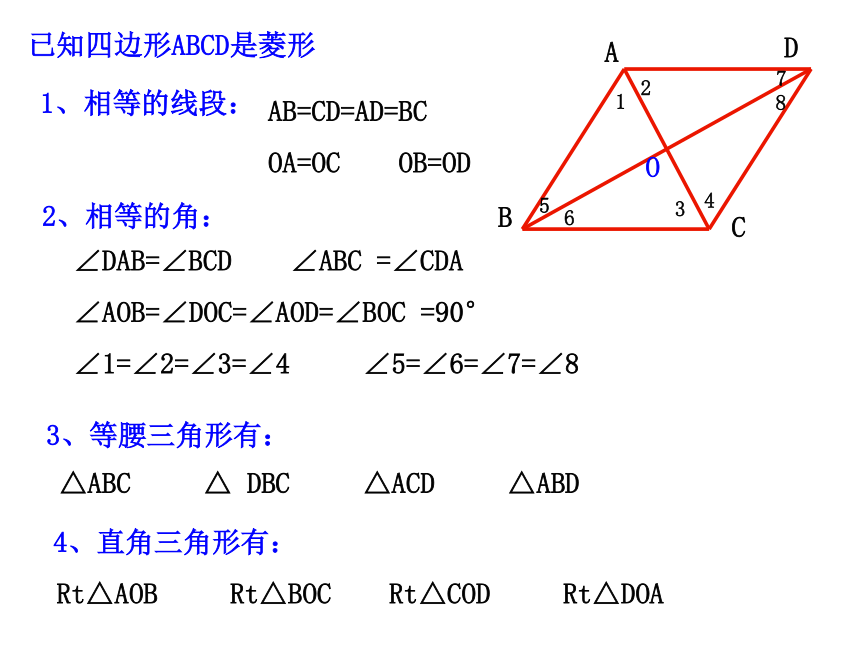
已知四边形ABCD是菱形
1、相等的线段:
AB=CD=AD=BC
OA=OC OB=OD
2、相等的角:
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
3、等腰三角形有:
△ABC △ DBC △ACD △ABD
4、直角三角形有:
Rt△AOB Rt△BOC Rt△COD Rt△DOA
A
B
C
D
O
1
2
3
4
5
6
7
8
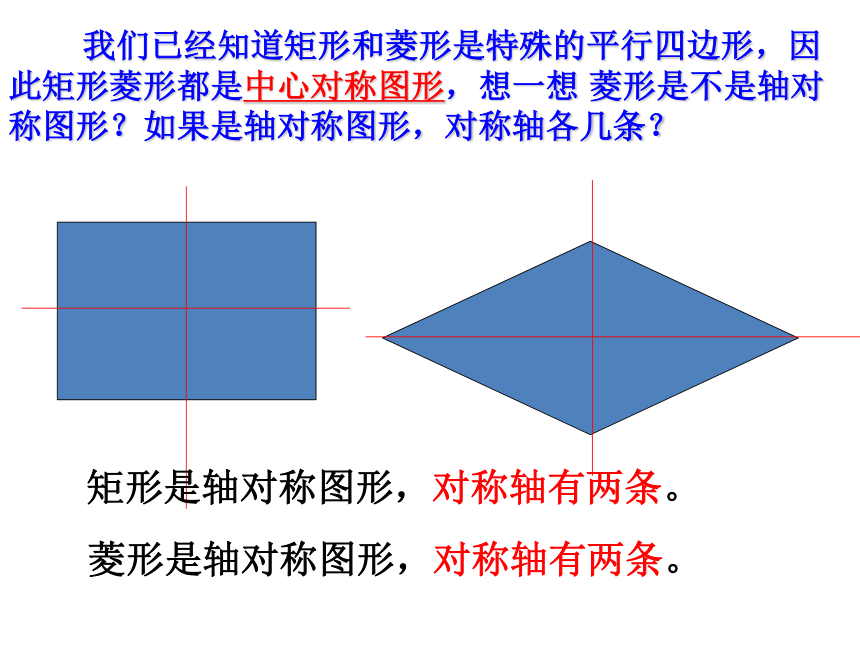
我们已经知道矩形和菱形是特殊的平行四边形,因此矩形菱形都是中心对称图形,想一想 菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条?
矩形是轴对称图形,对称轴有两条。
菱形是轴对称图形,对称轴有两条。
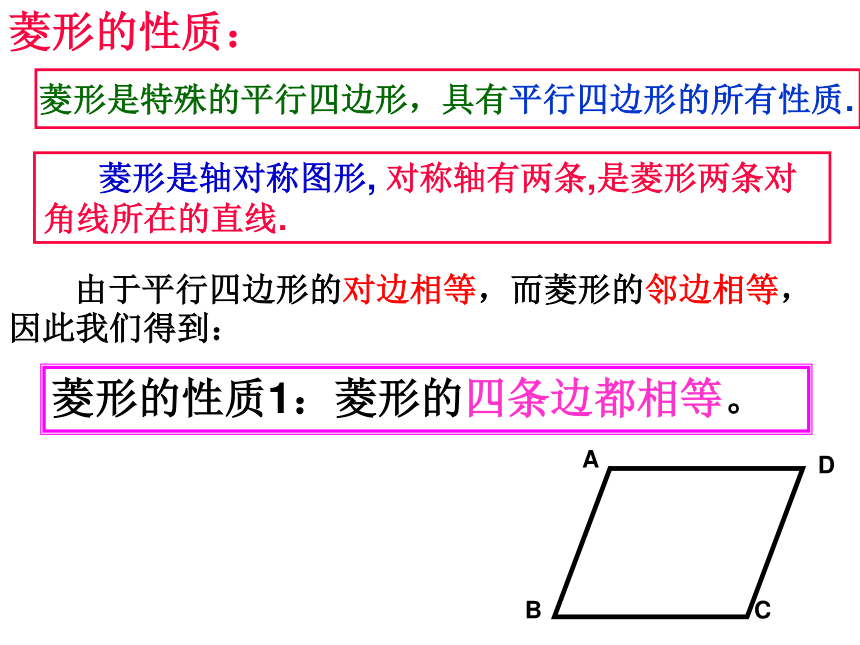
由于平行四边形的对边相等,而菱形的邻边相等,因此我们得到:
菱形的性质1:菱形的四条边都相等。
A
B
D
C
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质:
菱形是轴对称图形, 对称轴有两条,是菱形两条对角线所在的直线.
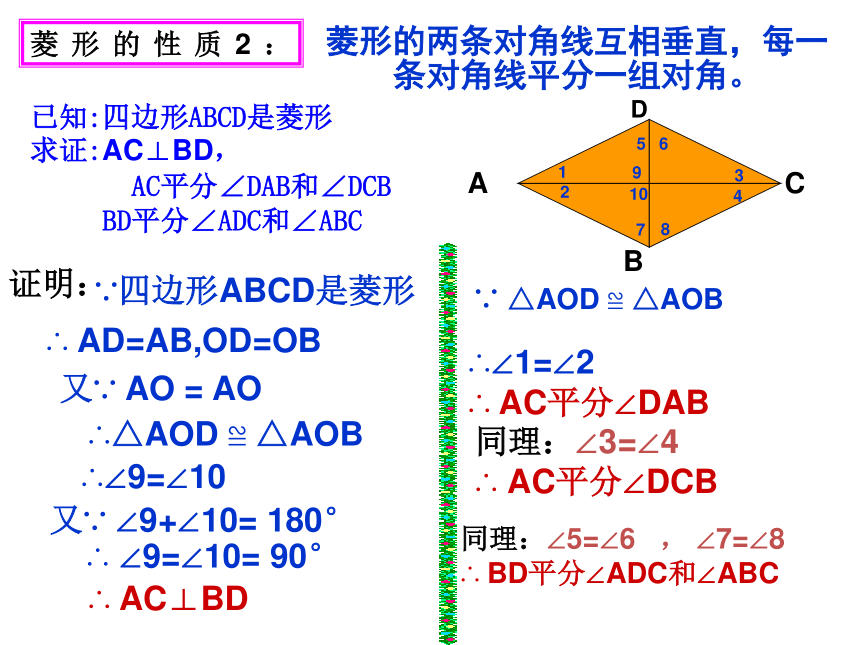
菱形的两条对角线互相垂直,每一条对角线平分一组对角。
∵四边形ABCD是菱形
∴ AD=AB,OD=OB
∴ AC⊥BD
∴∠9=∠10
又∵ AO = AO
∴△AOD ≌ △AOB
∵ △AOD ≌ △AOB
∴∠1=∠2
∴ AC平分∠DAB
同理:∠5=∠6 , ∠7=∠8
∴ BD平分∠ADC和∠ABC
∴ ∠9=∠10= 90°
已知:四边形ABCD是菱形
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
证明:
菱形的性质2:
O
6
又∵ ∠9+∠10= 180°
C
B
D
A
10
1
2
4
3
5
7
9
8
6
同理:∠3=∠4
∴ AC平分∠DCB
菱形的性质
(1)菱形具有平行四边形的一切性质;
(2)菱形的四条边都相等;
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
(4)菱形是轴对称图形,也是中心对称图形;
B
C
D
A
A
D
C
B
O
边
角
对角线
对称性
菱形的两组对边平行且相等
几何语言
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
菱形的四条边相等
∴ AB=BC=CD=DA
菱形的两组对角分别相等
∴ ∠DAB=∠DCB
∠ADC=∠ABC
菱形的邻角互补
∴ ∠DAB+∠ABC= 180°
菱形的两条对角线互相平分
∴ OA=OC;OB=OD
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
∴ AC⊥BD
∠1=∠2
∠3=∠4
∠5=∠6
∠7=∠8
菱形是中心对称图形,对称中心是两条对角线的交点。
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。
1
2
4
3
5
7
6
8
如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2 )
B
A
O
C
菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
C
B
D
A
O
分析:
你有什么发现?
菱
形
A
B
C
D
O
E
S菱形=BC·AE
思考:
计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
练习:已知一个菱形的周长是20 cm,两条对角线的比是4∶3,则这个菱形的面积是( )
(A)12 cm2 (B)24 cm2
(C)48 cm2 (D)96 cm2
【解析】选B.∵菱形的周长为20 cm,∴菱形的边长为5 cm,
设OA=4x cm,OB=3x cm,
则(4x)2+(3x)2=52.解得x=1,∴OA=4 cm,OB=3 cm,
∴AC=8 cm,
BD=6 cm,
∴菱形的面积= ×6×8=24(cm2).
一、菱形的定义
有一组邻边相等的平行四边形叫做菱形.
二、菱形的性质
1.菱形的四条边都相等
2.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形的面积等于它的两条对角线之积的一半.
三、反馈练习
4
5. 若菱形的边长为2,则这个菱形两条对角线的平方和为( )
(A)16 (B)8 (C)4 (D)1
【解析】选A.设这个菱形两条对角线长分别为a,b.由菱形对角线互相垂直且平分,则 即a2+b2=16.
6. 如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4 cm,则点P到BC的距离是____cm.
【解析】菱形对角线平分一组对角,且角平分线上的点到角两边的距离相等,故点P到BC的距离是4 cm.
四、小结测试
1.下列命题中正确的是( ),
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
解析:选项A,B不能判定是菱形;选项C,对角线相等的平行四边形应 是矩形,所以C错误,故选D.
答案:D
2.(2011·江苏无锡中考)菱形具有而矩形不一定具有的性质是( ).
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.对角互补
答案:A
3.如图所示,在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的边 长为( ).
A.5
B.6
C.8
D.10
解析:因为菱形的对角线互相垂直且平分,所以在Rt△AOB中,根据勾 股定理可得AB= = =5,即菱形的边长为5.
答案:A
4.如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周 长为( ).
A.20 B.18
C.16 D.15
解析:由题意可知,△ABC是等边三角形,
所以AB=BC=AC=4.
因为菱形的四条边都相等,故菱形ABCD的周长为16.
答案:C
5.(2011·广州中考)如图,AC是菱形ABCD的对角线,点E,F分别在边 AB,AD上,且AE=AF.
求证:△ACE≌△ACF.
证明:∵四边形ABCD为菱形,
∴∠BAC=∠DAC.
又∵AE=AF,AC=AC,
∴△ACE≌△ACF(SAS).
6.已知在菱形ABCD中,O是对角线BD上的一动点.如图,P为线段BC 上一点,连接PO,并延长交AD于点Q,当O是BD的中点时,求证:OP=OQ.
证明:∵四边形ABCD为菱形,∴AD∥BC.
∴∠OBP=∠ODQ.
∵O是BD的中点,∴OB=OD.
在△BOP和△DOQ中,
∵∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ,
∴△BOP≌△DOQ(ASA),∴OP=OQ.
五、作业
课本102页:5、11、12
不抄题,画图
3.如图(1),在矩形ABCD中,动点P从点B出发,
沿BC,CD,DA运动至点A停止,设点P运动的路程为x,
△ABP的面积为y,如果y关于x的函数图象如图(2)所示,
则矩形ABCD的面积是( ).
A.10 B.16 C.20 D.36
解析:由图可知,BC=4,CD=9-4=5,则矩形ABCD的面积是20.
答案:C
8.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的
延长线于点F.
(1)求证:AB=CF;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
(1)证明:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∴∠BAE=∠CFE,∠ABE=∠FCE.
∵E为BC的中点,
∴EB=EC.
∴△ABE≌△FCE.
∴AB=CF.
(2)解:当BC=AF时,四边形ABFC是矩形.
理由如下:
∵AB∥CF,AB=CF,
∴四边形ABFC是平行四边形.
∵BC=AF,
∴四边形ABFC是矩形.
19.2.2 菱形
A
B
C
D
O
地调学校数学教研组
1.矩形的性质:(1)矩形的四个角都是____;(2)矩形的对角线____.
学 前 温 故
2.矩形的判定:(1)有一个角是直角的__________是矩形;(2)对角线_______的平行四边形是矩形.
直角
相等
平行四边形
相
等
一、预习与反馈
1.菱形的概念
有一组邻边 的平行四边形叫做菱形.
相等
新 课 早 知
2.菱形的性质
菱形的四条边都 ;菱形的两条对角线 ,并且每 一条对角线平分一组 .
对角
相等
互相垂直
两组对边
分别平行
平行
四边形
矩形
前面我们学行四边形和矩形,知道了如果平行四边形有一个角是直角时,成为什么图形
菱形
(矩形,由角变化得到)
如果从边的角度,将平行四边形特殊化,让它有一组邻边相等,这个特殊的四边形叫什么呢
(菱形,由边变化得到)
四边形
情景创设
平行四边形
菱形
邻边相等
二、新课精讲
有一组邻边相等的平行四边形叫做菱形;
AB=BC
四边形ABCD是菱形
□ ABCD
菱形的定义
小明是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
1、图中有哪些相等的线段?
2、图中有哪些相等的角?
3、图中有哪些等腰三角形?
4、图中有哪些直角三角形?
5、菱形是轴对称图形吗?它有几条对称轴?分别是什么?对称轴间有什么关系?
已知四边形ABCD是菱形
A
B
C
D
O
1
2
3
4
5
6
7
8
已知四边形ABCD是菱形
1、相等的线段:
AB=CD=AD=BC
OA=OC OB=OD
2、相等的角:
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
3、等腰三角形有:
△ABC △ DBC △ACD △ABD
4、直角三角形有:
Rt△AOB Rt△BOC Rt△COD Rt△DOA
A
B
C
D
O
1
2
3
4
5
6
7
8
我们已经知道矩形和菱形是特殊的平行四边形,因此矩形菱形都是中心对称图形,想一想 菱形是不是轴对称图形?如果是轴对称图形,对称轴各几条?
矩形是轴对称图形,对称轴有两条。
菱形是轴对称图形,对称轴有两条。
由于平行四边形的对边相等,而菱形的邻边相等,因此我们得到:
菱形的性质1:菱形的四条边都相等。
A
B
D
C
菱形是特殊的平行四边形,具有平行四边形的所有性质.
菱形的性质:
菱形是轴对称图形, 对称轴有两条,是菱形两条对角线所在的直线.
菱形的两条对角线互相垂直,每一条对角线平分一组对角。
∵四边形ABCD是菱形
∴ AD=AB,OD=OB
∴ AC⊥BD
∴∠9=∠10
又∵ AO = AO
∴△AOD ≌ △AOB
∵ △AOD ≌ △AOB
∴∠1=∠2
∴ AC平分∠DAB
同理:∠5=∠6 , ∠7=∠8
∴ BD平分∠ADC和∠ABC
∴ ∠9=∠10= 90°
已知:四边形ABCD是菱形
求证:AC⊥BD,
AC平分∠DAB和∠DCB
BD平分∠ADC和∠ABC
证明:
菱形的性质2:
O
6
又∵ ∠9+∠10= 180°
C
B
D
A
10
1
2
4
3
5
7
9
8
6
同理:∠3=∠4
∴ AC平分∠DCB
菱形的性质
(1)菱形具有平行四边形的一切性质;
(2)菱形的四条边都相等;
(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
(4)菱形是轴对称图形,也是中心对称图形;
B
C
D
A
A
D
C
B
O
边
角
对角线
对称性
菱形的两组对边平行且相等
几何语言
∵四边形ABCD是菱形
∥
=
∴ AD BC
AB CD
∥
=
菱形的四条边相等
∴ AB=BC=CD=DA
菱形的两组对角分别相等
∴ ∠DAB=∠DCB
∠ADC=∠ABC
菱形的邻角互补
∴ ∠DAB+∠ABC= 180°
菱形的两条对角线互相平分
∴ OA=OC;OB=OD
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
∴ AC⊥BD
∠1=∠2
∠3=∠4
∠5=∠6
∠7=∠8
菱形是中心对称图形,对称中心是两条对角线的交点。
菱形是轴对称图形,有2条对称轴,是两条对角线所在的直线。
1
2
4
3
5
7
6
8
如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2 )
B
A
O
C
菱形ABCD两条对角线BD、AC长分别是6cm和8cm,求菱形的周长和面积。
C
B
D
A
O
分析:
你有什么发现?
菱
形
A
B
C
D
O
E
S菱形=BC·AE
思考:
计算菱形的面积除了上式方法外,利用对角线能计算菱形的面积吗
= S△ABD+S△BCD = AC×BD
S菱形ABCD
菱形的面积=底×高=对角线乘积的一半
练习:已知一个菱形的周长是20 cm,两条对角线的比是4∶3,则这个菱形的面积是( )
(A)12 cm2 (B)24 cm2
(C)48 cm2 (D)96 cm2
【解析】选B.∵菱形的周长为20 cm,∴菱形的边长为5 cm,
设OA=4x cm,OB=3x cm,
则(4x)2+(3x)2=52.解得x=1,∴OA=4 cm,OB=3 cm,
∴AC=8 cm,
BD=6 cm,
∴菱形的面积= ×6×8=24(cm2).
一、菱形的定义
有一组邻边相等的平行四边形叫做菱形.
二、菱形的性质
1.菱形的四条边都相等
2.菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形的面积等于它的两条对角线之积的一半.
三、反馈练习
4
5. 若菱形的边长为2,则这个菱形两条对角线的平方和为( )
(A)16 (B)8 (C)4 (D)1
【解析】选A.设这个菱形两条对角线长分别为a,b.由菱形对角线互相垂直且平分,则 即a2+b2=16.
6. 如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4 cm,则点P到BC的距离是____cm.
【解析】菱形对角线平分一组对角,且角平分线上的点到角两边的距离相等,故点P到BC的距离是4 cm.
四、小结测试
1.下列命题中正确的是( ),
A.对角线相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线相等的平行四边形是菱形
D.对角线互相垂直的平行四边形是菱形
解析:选项A,B不能判定是菱形;选项C,对角线相等的平行四边形应 是矩形,所以C错误,故选D.
答案:D
2.(2011·江苏无锡中考)菱形具有而矩形不一定具有的性质是( ).
A.对角线互相垂直
B.对角线相等
C.对角线互相平分
D.对角互补
答案:A
3.如图所示,在菱形ABCD中,两条对角线AC=6,BD=8,则此菱形的边 长为( ).
A.5
B.6
C.8
D.10
解析:因为菱形的对角线互相垂直且平分,所以在Rt△AOB中,根据勾 股定理可得AB= = =5,即菱形的边长为5.
答案:A
4.如图,在菱形ABCD中,对角线AC=4,∠BAD=120°,则菱形ABCD的周 长为( ).
A.20 B.18
C.16 D.15
解析:由题意可知,△ABC是等边三角形,
所以AB=BC=AC=4.
因为菱形的四条边都相等,故菱形ABCD的周长为16.
答案:C
5.(2011·广州中考)如图,AC是菱形ABCD的对角线,点E,F分别在边 AB,AD上,且AE=AF.
求证:△ACE≌△ACF.
证明:∵四边形ABCD为菱形,
∴∠BAC=∠DAC.
又∵AE=AF,AC=AC,
∴△ACE≌△ACF(SAS).
6.已知在菱形ABCD中,O是对角线BD上的一动点.如图,P为线段BC 上一点,连接PO,并延长交AD于点Q,当O是BD的中点时,求证:OP=OQ.
证明:∵四边形ABCD为菱形,∴AD∥BC.
∴∠OBP=∠ODQ.
∵O是BD的中点,∴OB=OD.
在△BOP和△DOQ中,
∵∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ,
∴△BOP≌△DOQ(ASA),∴OP=OQ.
五、作业
课本102页:5、11、12
不抄题,画图
