19.2.2菱形的判定
图片预览

文档简介
(共22张PPT)
19.2.2 菱形的判定
A
B
C
D
O
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
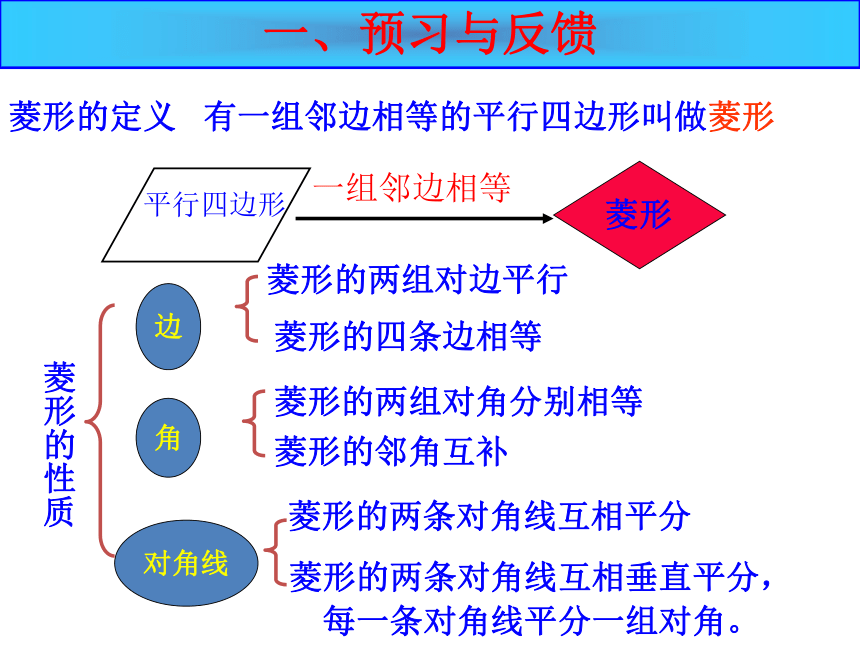
菱形的定义
菱形的性质
菱形
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
每一条对角线平分一组对角。
一、预习与反馈
菱形的判定
(1)一组 相等的平行四边形是菱形.
(2)对角线 的平行四边形是菱形.
(3)四边 的四边形是菱形.
邻边
互相垂直
相等
二、新课精讲
菱形的判别
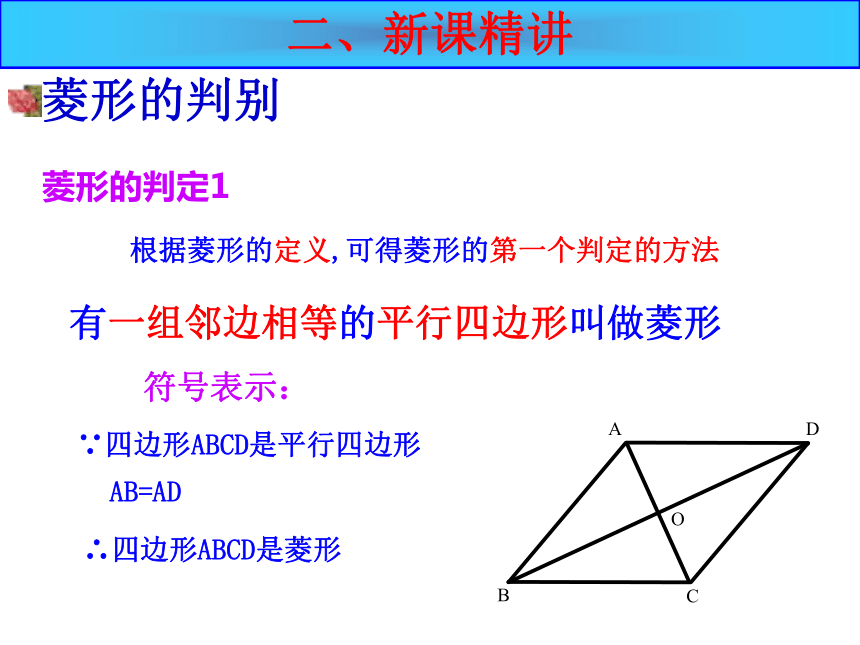
根据菱形的定义,可得菱形的第一个判定的方法
AB=AD
∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
符号表示:
有一组邻边相等的平行四边形叫做菱形
菱形的判定1
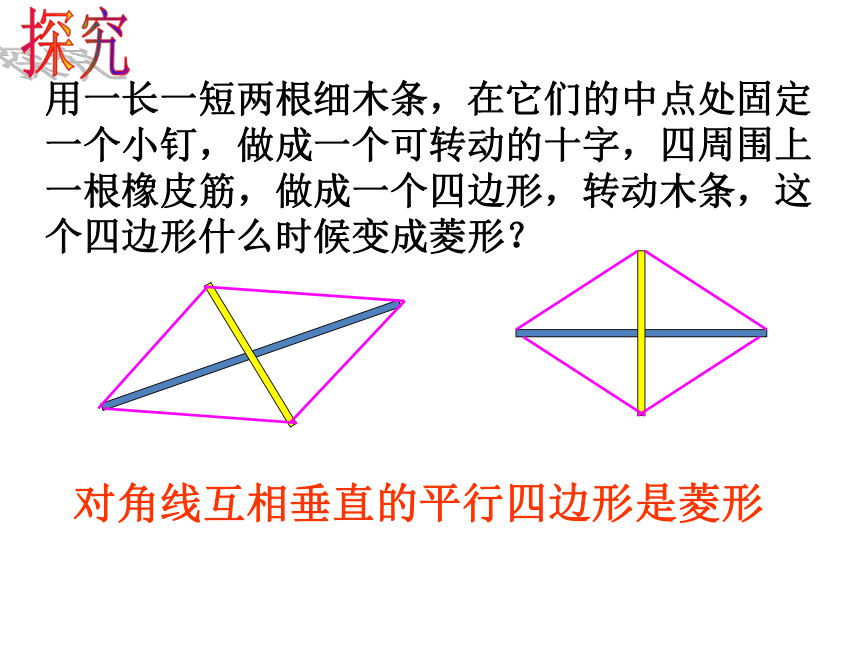
用一长一短两根细木条,在它们的中点处固定
一个小钉,做成一个可转动的十字,四周围上
一根橡皮筋,做成一个四边形,转动木条,这
个四边形什么时候变成菱形?
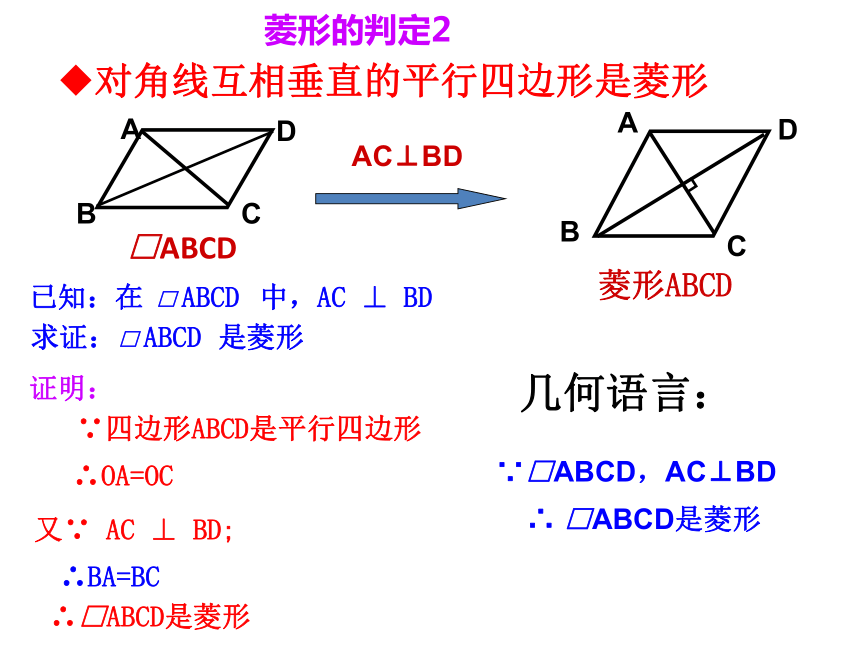
对角线互相垂直的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵□ABCD,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定2
证明:
∴□ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
求证: 是菱形
已知:在 中,AC ⊥ BD
□ ABCD
□ ABCD
几何语言:
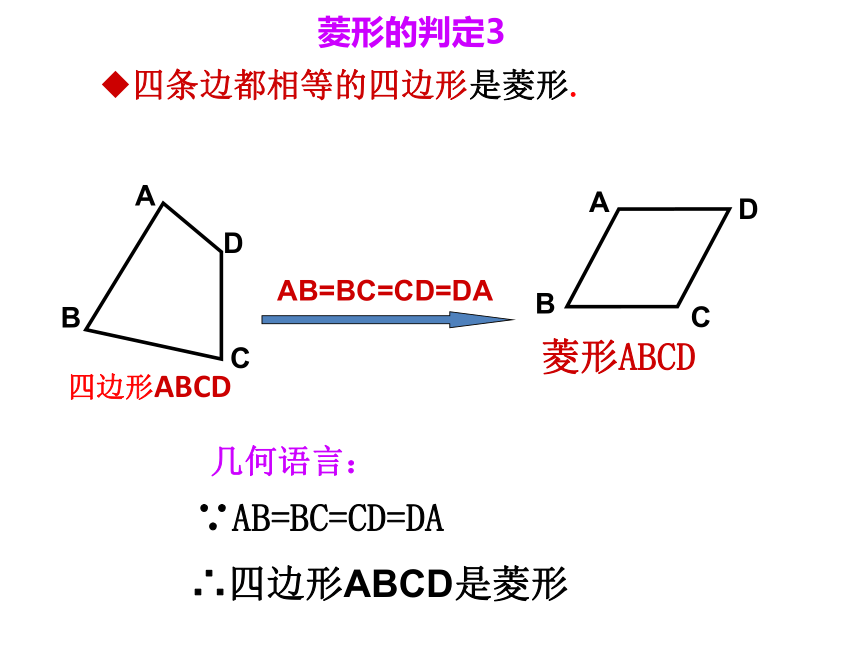
四条边都相等的四边形是菱形.
四边形ABCD
A
B
C
D
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵AB=BC=CD=DA
∴四边形ABCD是菱形
菱形的判定3
几何语言:
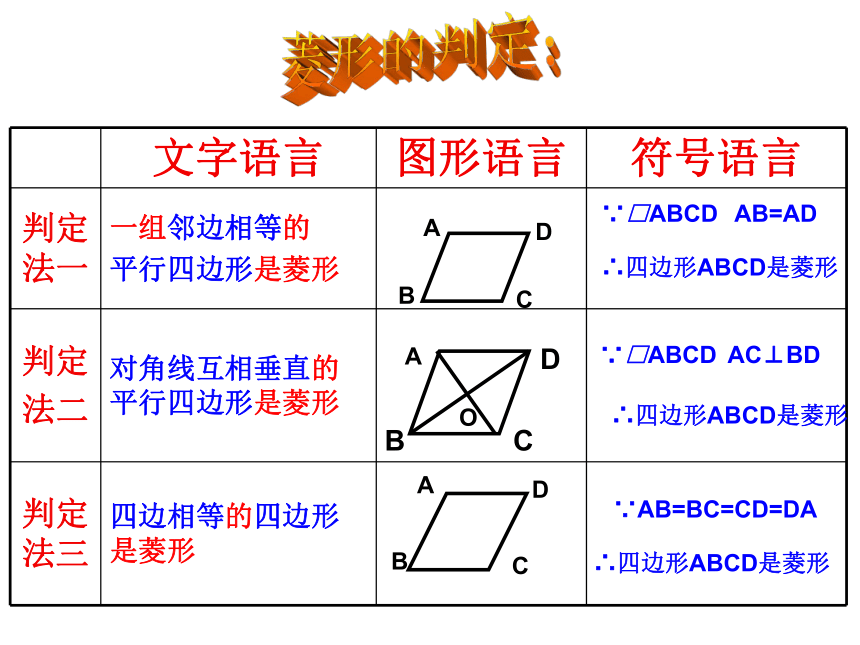
文字语言 图形语言 符号语言
判定法一 一组邻边相等的
平行四边形是菱形
判定
法二 对角线互相垂直的平行四边形是菱形
判定法三 四边相等的四边形是菱形
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵□ABCD
AC⊥BD
∴四边形ABCD是菱形
∵□ABCD
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
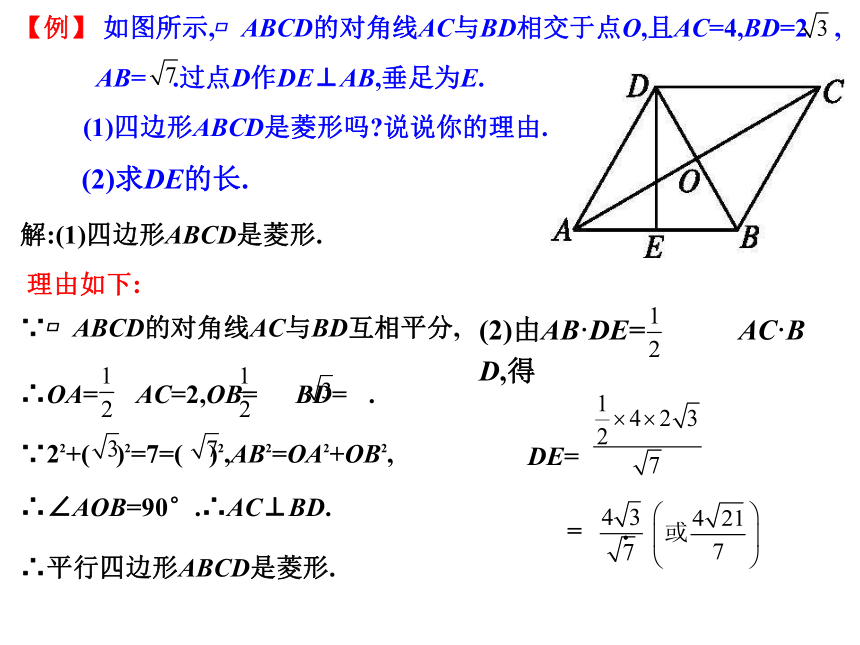
【例】 如图所示, ABCD的对角线AC与BD相交于点O,且AC=4,BD=2 ,
AB= .过点D作DE⊥AB,垂足为E.
(1)四边形ABCD是菱形吗 说说你的理由.
(2)求DE的长.
解:(1)四边形ABCD是菱形.
理由如下:
∵ ABCD的对角线AC与BD互相平分,
∴∠AOB=90°.∴AC⊥BD.
∴OA= AC=2,OB= BD= .
∵22+( )2=7=( )2,AB2=OA2+OB2,
∴平行四边形ABCD是菱形.
DE=
= .
(2)由AB·DE= AC·BD,得
A
B
C
D
O
例3. 如图,平行四边形ABCD的对角线AC、BD交于O,AB=5,AO=4,BO=3。
求证:平行四边形ABCD是菱形。
a
已知:线段a,求作:一个菱形ABCD,
使AB=a,∠ABC=∠
B
C
A
D
作法:1.作∠ B =∠
2.在∠B的两边上分别截取
AB=BC=a,
3.分别以A、C为圆心,a长
为半径画弧,两弧交于点D,
连结AD、CD
∴四边形ABCD就是所作的菱形
这样作出的四边形ABCD真的是菱形吗?
你会证明吗?
你能否用一句话来概括?
四边相等的四边形是菱形
数学语言
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
思考:把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
A
D
C
B
∟
∟
E
F
归纳
菱形常用的判定方法:
1、有一组邻边相等的平行四边形叫做菱形.
2、对角线互相垂直的平行四边形是菱形.
(对角线互相垂直平分的四边形是菱形.)
3、有四条边相等的四边形是菱形.
1.□ ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形.
A
B
C
D
O
矩
菱
矩
菱
三、反馈练习
2
3. 如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
(A)BA=BC (B)AC、BD互相平分
(C)AC=BD (D)AB∥CD
【解析】选B.对角线互相垂直且平分的四边形是菱形.
4.□ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB=BC;③AC平分∠BAD;④AO=DO,使得□ABCD是菱形的条件有____________.(填序号)
【解析】添加①符合对角线互相垂直的平行四边形是菱形;由③可证BA=BC或DA=DC,因此添加②③符合菱形的定义.添加④只能得对角线相等,这是证矩形的条件.
答案:①②③
5.如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为_______.
【解析】由E、F、G、H分别为矩形的边的中点,
可得四边形EFGH是菱形,
∴阴影部分的面积为 ×2×4=4.
4
6
7
8. 如图,在□ ABCD中,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于点E、F.已知BE=BP.
求证:(1)∠E=∠F;(2)□ ABCD是菱形.
四、小结测试
6.已知在菱形ABCD中,O是对角线BD上的一动点.如图,P为线段BC上一点,连接PO,并延长交AD于点Q,当O是BD的中点时,求证:OP=OQ.
证明:∵四边形ABCD为菱形,∴AD∥BC.
∴∠OBP=∠ODQ.
∵O是BD的中点,∴OB=OD.
在△BOP和△DOQ中,
∵∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ,
∴△BOP≌△DOQ(ASA),∴OP=OQ.
7.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
解:(1)四边形OCED是菱形.理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)连接OE,由菱形OCED得CD⊥OE,
∴OE∥BC.
又CE∥BD,∴四边形BCEO是平行四边形.
∴OE=BC=8,
∴S四边形OCED= OE·CD= ×8×6=24.
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
A
B
C
D
E
F
你敢挑战吗?
回去想一想
老师说下列三个图形都是菱形,你相信吗
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
3
3
4
4
┍
19.2.2 菱形的判定
A
B
C
D
O
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
菱形的定义
菱形的性质
菱形
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直平分,
每一条对角线平分一组对角。
一、预习与反馈
菱形的判定
(1)一组 相等的平行四边形是菱形.
(2)对角线 的平行四边形是菱形.
(3)四边 的四边形是菱形.
邻边
互相垂直
相等
二、新课精讲
菱形的判别
根据菱形的定义,可得菱形的第一个判定的方法
AB=AD
∵四边形ABCD是平行四边形
∴四边形ABCD是菱形
符号表示:
有一组邻边相等的平行四边形叫做菱形
菱形的判定1
用一长一短两根细木条,在它们的中点处固定
一个小钉,做成一个可转动的十字,四周围上
一根橡皮筋,做成一个四边形,转动木条,这
个四边形什么时候变成菱形?
对角线互相垂直的平行四边形是菱形
对角线互相垂直的平行四边形是菱形
AC⊥BD
∵□ABCD,AC⊥BD
∴ □ABCD是菱形
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
菱形的判定2
证明:
∴□ABCD是菱形
又∵ AC ⊥ BD;
∵四边形ABCD是平行四边形
∴OA=OC
∴BA=BC
求证: 是菱形
已知:在 中,AC ⊥ BD
□ ABCD
□ ABCD
几何语言:
四条边都相等的四边形是菱形.
四边形ABCD
A
B
C
D
AB=BC=CD=DA
A
B
C
D
菱形ABCD
∵AB=BC=CD=DA
∴四边形ABCD是菱形
菱形的判定3
几何语言:
文字语言 图形语言 符号语言
判定法一 一组邻边相等的
平行四边形是菱形
判定
法二 对角线互相垂直的平行四边形是菱形
判定法三 四边相等的四边形是菱形
A
B
C
D
∵AB=BC=CD=DA
∴四边形ABCD是菱形
∵□ABCD
AC⊥BD
∴四边形ABCD是菱形
∵□ABCD
AB=AD
∴四边形ABCD是菱形
A
B
C
D
O
A
B
C
D
【例】 如图所示, ABCD的对角线AC与BD相交于点O,且AC=4,BD=2 ,
AB= .过点D作DE⊥AB,垂足为E.
(1)四边形ABCD是菱形吗 说说你的理由.
(2)求DE的长.
解:(1)四边形ABCD是菱形.
理由如下:
∵ ABCD的对角线AC与BD互相平分,
∴∠AOB=90°.∴AC⊥BD.
∴OA= AC=2,OB= BD= .
∵22+( )2=7=( )2,AB2=OA2+OB2,
∴平行四边形ABCD是菱形.
DE=
= .
(2)由AB·DE= AC·BD,得
A
B
C
D
O
例3. 如图,平行四边形ABCD的对角线AC、BD交于O,AB=5,AO=4,BO=3。
求证:平行四边形ABCD是菱形。
a
已知:线段a,求作:一个菱形ABCD,
使AB=a,∠ABC=∠
B
C
A
D
作法:1.作∠ B =∠
2.在∠B的两边上分别截取
AB=BC=a,
3.分别以A、C为圆心,a长
为半径画弧,两弧交于点D,
连结AD、CD
∴四边形ABCD就是所作的菱形
这样作出的四边形ABCD真的是菱形吗?
你会证明吗?
你能否用一句话来概括?
四边相等的四边形是菱形
数学语言
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
思考:把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
A
D
C
B
∟
∟
E
F
归纳
菱形常用的判定方法:
1、有一组邻边相等的平行四边形叫做菱形.
2、对角线互相垂直的平行四边形是菱形.
(对角线互相垂直平分的四边形是菱形.)
3、有四条边相等的四边形是菱形.
1.□ ABCD的对角线AC与BD相交于点O,
(1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形.
A
B
C
D
O
矩
菱
矩
菱
三、反馈练习
2
3. 如图,四边形ABCD的对角线AC、BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )
(A)BA=BC (B)AC、BD互相平分
(C)AC=BD (D)AB∥CD
【解析】选B.对角线互相垂直且平分的四边形是菱形.
4.□ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB=BC;③AC平分∠BAD;④AO=DO,使得□ABCD是菱形的条件有____________.(填序号)
【解析】添加①符合对角线互相垂直的平行四边形是菱形;由③可证BA=BC或DA=DC,因此添加②③符合菱形的定义.添加④只能得对角线相等,这是证矩形的条件.
答案:①②③
5.如图,在矩形ABCD中,E、F、G、H分别为边AB、BC、CD、DA的中点.若AB=2,AD=4,则图中阴影部分的面积为_______.
【解析】由E、F、G、H分别为矩形的边的中点,
可得四边形EFGH是菱形,
∴阴影部分的面积为 ×2×4=4.
4
6
7
8. 如图,在□ ABCD中,EF∥BD,分别交BC,CD于点P,Q,交AB,AD的延长线于点E、F.已知BE=BP.
求证:(1)∠E=∠F;(2)□ ABCD是菱形.
四、小结测试
6.已知在菱形ABCD中,O是对角线BD上的一动点.如图,P为线段BC上一点,连接PO,并延长交AD于点Q,当O是BD的中点时,求证:OP=OQ.
证明:∵四边形ABCD为菱形,∴AD∥BC.
∴∠OBP=∠ODQ.
∵O是BD的中点,∴OB=OD.
在△BOP和△DOQ中,
∵∠OBP=∠ODQ,OB=OD,∠BOP=∠DOQ,
∴△BOP≌△DOQ(ASA),∴OP=OQ.
7.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=6,BC=8,求四边形OCED的面积.
解:(1)四边形OCED是菱形.理由如下:
∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形,
又在矩形ABCD中,OC=OD,
∴四边形OCED是菱形.
(2)连接OE,由菱形OCED得CD⊥OE,
∴OE∥BC.
又CE∥BD,∴四边形BCEO是平行四边形.
∴OE=BC=8,
∴S四边形OCED= OE·CD= ×8×6=24.
如图,边长为a的菱形ABCD中,∠DAB=60度,E是异于A、D两点的动点,F是CD上的动点,满足AE+CF=a。
证明:不论E、F怎样移动,三角形BEF总是正三角形。
A
B
C
D
E
F
你敢挑战吗?
回去想一想
老师说下列三个图形都是菱形,你相信吗
5
5
3
4
3
4
5
5
5
5
有一组邻边相等的平行四边形叫做菱形
对角线互相垂直的平行四边形是菱形
有四条边相等的四边形是菱形。
3
3
4
4
┍
