辽宁省辽西县高中2020-2021学年高一下学期6月第二次月考数学试题 图片版含答案
文档属性
| 名称 | 辽宁省辽西县高中2020-2021学年高一下学期6月第二次月考数学试题 图片版含答案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 00:00:00 | ||
图片预览



文档简介
高一月考答案
1.B2.B3.B4.B5.A6.B7.B8.C
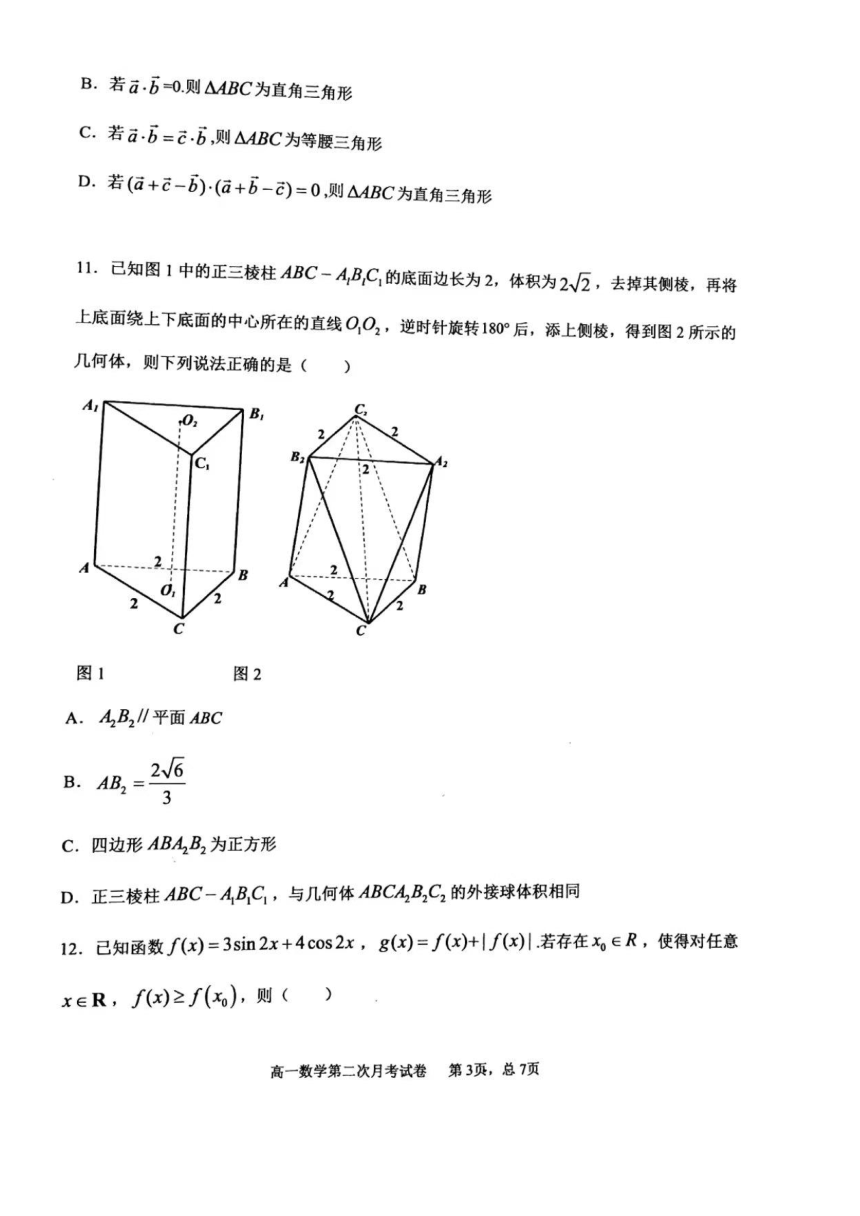
9.ABD10.BCD11.ACD12.BD
13.-1
14.15.16.
17.(1),;(2).
【分析】
(1)根据,即可得解;
(2)根据公式计算求解.
【详解】
(1)由题向量的夹角为60°,所以,
,
;
(2),
所以
【点睛】
此题考查平面向量数量积,根据定义计算两个向量的数量积,求向量的模长和根据数量积与模长关系求向量夹角.
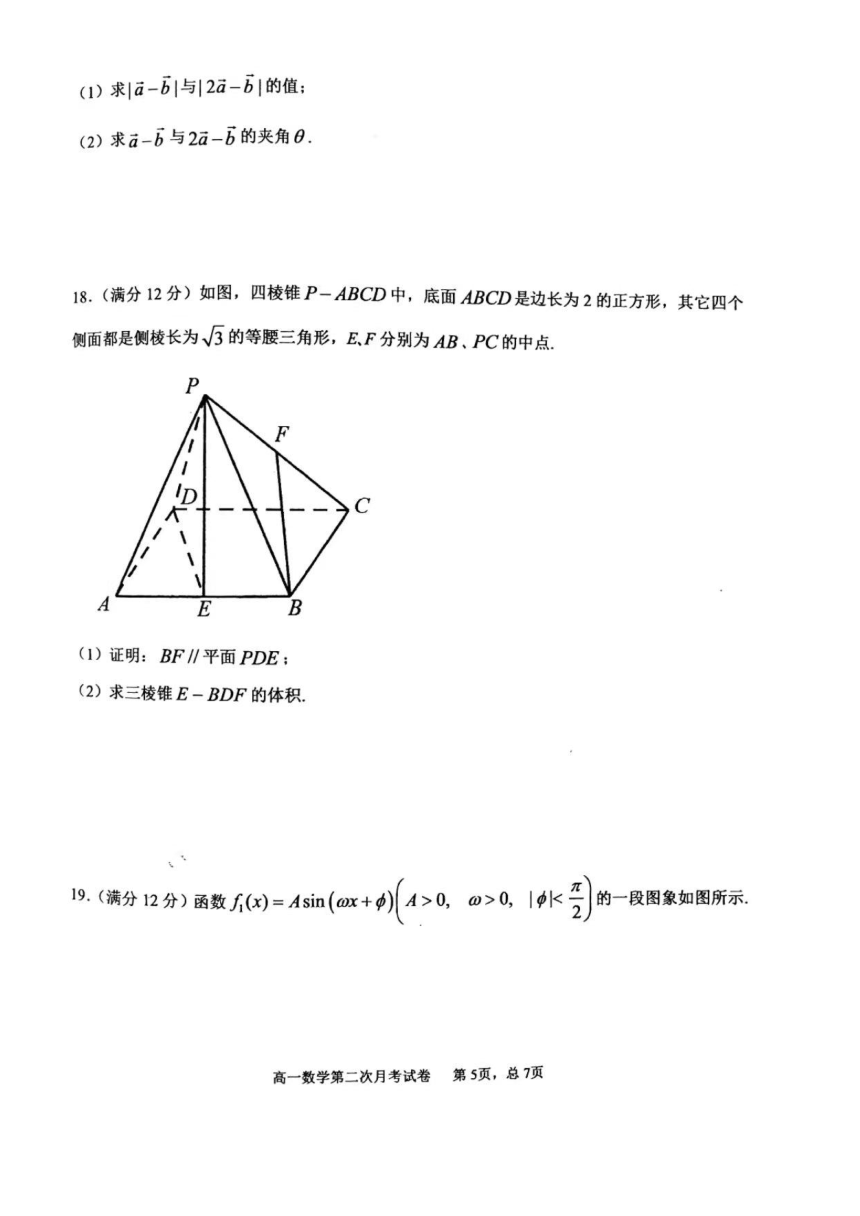
18.(1)证明见解析;(2).
【分析】
(1)取的中点,可得四边形是平行四边形得平面,为的中点,得平面,再由面面平行的判定定理可得平面平面,得线面平行;
(2)利用体积,求出,得解.
【详解】
证明:(1)取的中点为,连,
为正方形,为的中点,
且,四边形是平行四边形,,
平面,平面,所以平面,
为的中点,,
平面,平面,所以平面,
且,
平面平面,平面,平面,
平面.
(2)为正方形,且,
为正四棱锥,在平面的射影为的中点,
为的中点,,
,
,
,
.
【点睛】
本题考查了证明线面平行、求三棱锥的体积的问题,解题的关键点是利用等体积转化求体积,考查了学生了空间想象能力和计算能力.
19.(1);(2)
【分析】
(1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式;
(2)根据函数y=Asin(ωx+φ)的图象变换规律,求得函数y=f2(x)的解析式,由
,得到函数的单调增区间.
【详解】
(1)如图,由题意得,的最大值为2,
又,∴,即
∴.
因为的图像过最高点,则
即.
(2).依题意得:
∴由
解得:
,则的单调增区间为.
【点睛】
本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于中档题.
20.(1)证明见解析(2)存在,为的中点.
【分析】
(1)连接,则也为的中点,由可证平面;
(2)存在,为的中点时,平面平面,利用平面与平面平行的判定定理可证结论.
【详解】
(1)连接,则也为的中点,
因为为的中点,所以为△的中位线,
所以,又平面,平面,
所以平面.
(2)存在,为的中点时,平面平面,
证明:连,,
因为为的中点,为的中点,
所以,又平面,平面,
所以平面,
又由(1)知平面,且,
所以平面平面.
【点睛】
本题考查了直线与平面平行的判定定理,考查了平面与平面平行的判定定理,属于基础题.
21.(1)
(2)
【解析】
试题分析:(1)求出
,由正弦定理得
,由此能求出
;(2)推导出
,从而得到
,由此利用余弦定理能求出
的值.
试题解析:(1)在三角形中,∵cosB=,∴sinB=.
在△ABD中,由正弦定理得,
又AB=2,,sinB=.
∴AD=.
(2)∵BD=2DC,∴S△ABD=2S△ADC,S△ABC=3S△ADC,
又,∴
∵S△ABC=,∴BC=6,
∵,,[]
S△ABD=2S△ADC,∴,
在△ABC中,由余弦定理得:
AC2=AB2+BC2﹣2AB?BC?cos∠ABC,∴AC=4,
∴=2?=4.
22.(1)选①②③,;(2).
【分析】
(1)根据题意可得出函数的最小正周期,可求得的值,根据所选的条件得出关于的表达式,然后结合所选条件进行检验,求出的值,综合可得出函数的解析式;
(2)求得,由可计算得出,进而可得出,由参变量分离法得出,利用基本不等式求得的最小值,由此可得出实数的取值范围.
【详解】
(1)由题意可知,函数的最小正周期为,.
选①,因为函数的一条对称轴,则,
解得,
,所以,的可能取值为、.
若,则,则,不合乎题意;
若,则,则,合乎题意.
所以,;
选②,因为函数的一个对称中心,则,
解得,
,所以,的可能取值为、.
若,则,当时,,
此时,函数在区间上单调递增,不合乎题意;
若,则,当时,,
此时,函数在区间上单调递减,合乎题意;
所以,;
选③,将函数向左平移个单位得到的图象关于轴对称,
所得函数为,
由于函数的图象关于轴对称,可得,
解得,
,所以,的可能取值为、.
若,则,,不合乎题意;
若,则,,合乎题意.
所以,;
(2)由(1)可知,
所以,,
当时,,,所以,,
所以,,
,
,,则,
由可得,
所以,,
由基本不等式可得,
当且仅当时,等号成立,所以,.
【点睛】
结论点睛:利用参变量分离法求解函数不等式恒(能)成立,可根据以下原则进行求解:
(1),;
(2),;
(3),;
(4),.
1.B2.B3.B4.B5.A6.B7.B8.C
9.ABD10.BCD11.ACD12.BD
13.-1
14.15.16.
17.(1),;(2).
【分析】
(1)根据,即可得解;
(2)根据公式计算求解.
【详解】
(1)由题向量的夹角为60°,所以,
,
;
(2),
所以
【点睛】
此题考查平面向量数量积,根据定义计算两个向量的数量积,求向量的模长和根据数量积与模长关系求向量夹角.
18.(1)证明见解析;(2).
【分析】
(1)取的中点,可得四边形是平行四边形得平面,为的中点,得平面,再由面面平行的判定定理可得平面平面,得线面平行;
(2)利用体积,求出,得解.
【详解】
证明:(1)取的中点为,连,
为正方形,为的中点,
且,四边形是平行四边形,,
平面,平面,所以平面,
为的中点,,
平面,平面,所以平面,
且,
平面平面,平面,平面,
平面.
(2)为正方形,且,
为正四棱锥,在平面的射影为的中点,
为的中点,,
,
,
,
.
【点睛】
本题考查了证明线面平行、求三棱锥的体积的问题,解题的关键点是利用等体积转化求体积,考查了学生了空间想象能力和计算能力.
19.(1);(2)
【分析】
(1)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式;
(2)根据函数y=Asin(ωx+φ)的图象变换规律,求得函数y=f2(x)的解析式,由
,得到函数的单调增区间.
【详解】
(1)如图,由题意得,的最大值为2,
又,∴,即
∴.
因为的图像过最高点,则
即.
(2).依题意得:
∴由
解得:
,则的单调增区间为.
【点睛】
本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于中档题.
20.(1)证明见解析(2)存在,为的中点.
【分析】
(1)连接,则也为的中点,由可证平面;
(2)存在,为的中点时,平面平面,利用平面与平面平行的判定定理可证结论.
【详解】
(1)连接,则也为的中点,
因为为的中点,所以为△的中位线,
所以,又平面,平面,
所以平面.
(2)存在,为的中点时,平面平面,
证明:连,,
因为为的中点,为的中点,
所以,又平面,平面,
所以平面,
又由(1)知平面,且,
所以平面平面.
【点睛】
本题考查了直线与平面平行的判定定理,考查了平面与平面平行的判定定理,属于基础题.
21.(1)
(2)
【解析】
试题分析:(1)求出
,由正弦定理得
,由此能求出
;(2)推导出
,从而得到
,由此利用余弦定理能求出
的值.
试题解析:(1)在三角形中,∵cosB=,∴sinB=.
在△ABD中,由正弦定理得,
又AB=2,,sinB=.
∴AD=.
(2)∵BD=2DC,∴S△ABD=2S△ADC,S△ABC=3S△ADC,
又,∴
∵S△ABC=,∴BC=6,
∵,,[]
S△ABD=2S△ADC,∴,
在△ABC中,由余弦定理得:
AC2=AB2+BC2﹣2AB?BC?cos∠ABC,∴AC=4,
∴=2?=4.
22.(1)选①②③,;(2).
【分析】
(1)根据题意可得出函数的最小正周期,可求得的值,根据所选的条件得出关于的表达式,然后结合所选条件进行检验,求出的值,综合可得出函数的解析式;
(2)求得,由可计算得出,进而可得出,由参变量分离法得出,利用基本不等式求得的最小值,由此可得出实数的取值范围.
【详解】
(1)由题意可知,函数的最小正周期为,.
选①,因为函数的一条对称轴,则,
解得,
,所以,的可能取值为、.
若,则,则,不合乎题意;
若,则,则,合乎题意.
所以,;
选②,因为函数的一个对称中心,则,
解得,
,所以,的可能取值为、.
若,则,当时,,
此时,函数在区间上单调递增,不合乎题意;
若,则,当时,,
此时,函数在区间上单调递减,合乎题意;
所以,;
选③,将函数向左平移个单位得到的图象关于轴对称,
所得函数为,
由于函数的图象关于轴对称,可得,
解得,
,所以,的可能取值为、.
若,则,,不合乎题意;
若,则,,合乎题意.
所以,;
(2)由(1)可知,
所以,,
当时,,,所以,,
所以,,
,
,,则,
由可得,
所以,,
由基本不等式可得,
当且仅当时,等号成立,所以,.
【点睛】
结论点睛:利用参变量分离法求解函数不等式恒(能)成立,可根据以下原则进行求解:
(1),;
(2),;
(3),;
(4),.
同课章节目录
