内蒙古自治区赤峰市松山区四高2020-2021学年高二下学期6月第二次月考数学(文)试题 Word版含解析
文档属性
| 名称 | 内蒙古自治区赤峰市松山区四高2020-2021学年高二下学期6月第二次月考数学(文)试题 Word版含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 951.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-09 16:08:38 | ||
图片预览




文档简介
松山区第四中学高二年级下学期第二次月考数学试题(文科)
一、单选题,本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设false,则“false”是“false”的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.不充分也不必要条件
2.已知复数false,其中false若false为纯虚数,则( )
A.false B.false C.false D.false
3.某校初一有500名学生,为了培养学生良好的阅读习惯,学校要求他们从四大名著中选一本阅读,其中有200人选《三国演义》,125人选《水浒传》,125人选《西游记》,50人选《红楼梦》,若采用分层抽样的方法随机抽取40名学生分享他们的读后感,则选《西游记》的学生抽取的人数为( )
A.5 B.10 C.12 D.15
4.三个学生在校园内踢足球,“砰”的一声,不知道是谁踢的球把教室窗户的玻璃打破了,老师跑过来一看,问:“是谁打破了玻璃窗户”.甲说:“是乙打破的”;乙说:“是丙打破的”;丙说:“是乙打破的”,如果这三个孩子中只有一个人说了实话,则打破玻璃窗户的是( )
A.甲 B.乙 C.丙 D.不能确定
5.执行如图所示的程序框图,若输入false,则输出false的结果为( )
A.18 B.14 C.20 D.22
6.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A.false B.false C.false D.false
7.某学校为了解传统教学和教改实验的课堂教学情况,选取20.人平均分成同样水平的两组(甲组采用教改实验教学,乙组采用传统教学),一学期以后根据他们的期末成绩绘制茎叶图,如图所示,则( )
A.false,false B.false,false
C.false,false D.false,false
8.关于圆周率false,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计false的值:先请全校false名同学每人随机写下一个都小于1的正实数对false;再统计两数能与1构成钝角三角形三边的数对false的个数false;最后再根据统计数false估计false的值,那么可以估计false的值约为( )
A.false B.false C.false D.false
9.已知false的内角false的对边分别为false且falsefalse,false的面积为false则false( )
A.false B.5 C.8 D.false
10.设双曲线false的左、右焦点分别false、false,点false为双曲线右支上一点,false的内切圆圆心为false,则false的面积与false的面积之差为( )
A.false B.false C.false D.false
11.已知下列命题:
①回归直线false恒过样本点的中心false,且至少过一个样本点;
②两个变量相关性越强,则相关系数r就越接近于1;
③将一组数据的每个数据都加一个相同的常数后,方差不变;
④在回归直线方程false 中,当解释变量x增加一个单位时,预报变量false平均减少0.5;
⑤在线性回归模型中,相关指数false表示解释变量false对于预报变量false的贡献率,false越接近于1,表示回归效果越好;
⑥对分类变量false与false,它们的随机变量false的观测值false来说, false越小,“false与false有关系”的把握程度越大.
⑦两个模型中残差平方和越小的模型拟合的效果越好.
则正确命题的个数是( )
A.3 B.4 C.5 D.6
12.已知false,对false,且false,恒有false,则实数false的取值范围是( )
A.false B.false C.false D.false
二、填空题,本题共4小题,每小题5分,共20分.
13.统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如图所示,规定不低于60分为及格,则及格人数是_________________.
14.上饶市婺源县被誉为“茶乡”,婺源茶业千年不衰,新时代更是方兴未艾,其中由农业部监制的婺源大山顶特供茶“擂鼓峰茶尤为出名,为了解每壶“擂鼓峰”茶中所放茶叶量false克与食客的满意率false的关系,抽样得一组数据如下表:
false(克)
2
4
5
6
8
false(%)
30
false
50
70
60
根据表中的全部数据,用最小二乘法得出false与false的线性回归方程为false,则表中false的值为________.
15.F为抛物线false的焦点,点P在抛物线上,Q是圆false上的点,则false最小值是__________.
16.已知点false在曲线false(false是自然对数的底数)上,点false在曲线false上,则false的最小值为________.
三、解答题
17.已知公差不为0的等差数列false的前false项和为false,且false,false,false,false成等比数列.
(1)求数列false的通项公式;
(2)若数列false满足false,求数列false的前false项和false.
18.为进一步提升学生学习数学的热情,学校举行了数学学科知识竞赛.为了解学生对数学竞赛的喜爱程度是否与性别有关,现对高中部200名学生进行了问卷调查,得到如下2×2列联表:
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
女生
30
合计
已知在这200名学生中随机抽取1人,抽到喜欢数学竞赛的概率为0.6.
(1)将2×2列联表补充完整,并判断是否有90%的把握认为喜欢数学竞赛与性别有关?
(2)从上述不喜欢数学竞赛的学生中男生抽取3人,女生抽取2人,再在这5人中抽取3人,调查其喜欢的活动类型,求抽取的3人中至少有一名女生的概率.
参考公式及数据:false.
P(K2≥k)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.01
0.005
0.001
k
0.46
0.71
1.32
2.07
2.71
3.84
5.024
6.635
7.879
10.828
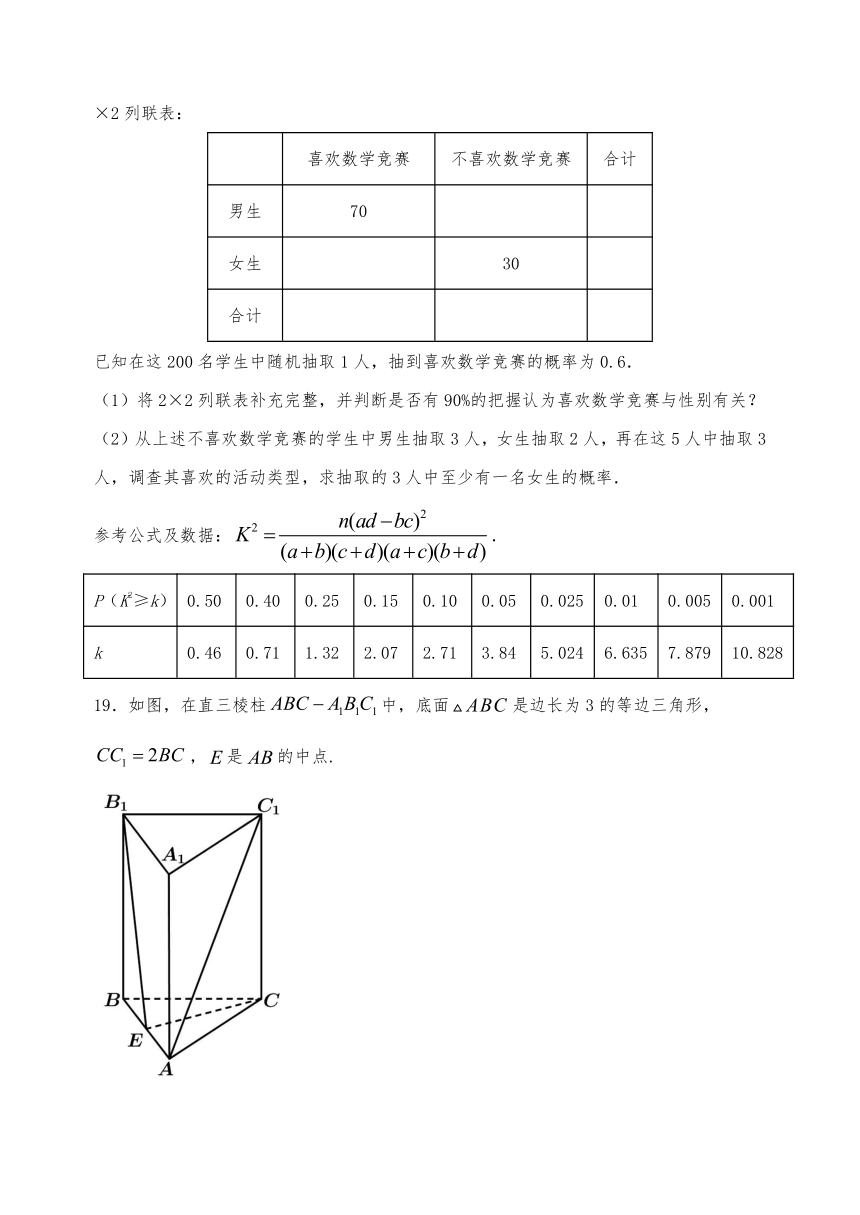
19.如图,在直三棱柱false中,底面false是边长为3的等边三角形,false,false是false的中点.
(Ⅰ)证明:false;
(Ⅱ)求四棱锥false的体积.
20.已知函数false.
(1)讨论函数false的单调性;
(2)证明:函数false(false为自然对数的底数)恒成立.
21.已知椭圆false:false的右顶点为false,上?下顶点分别是false,false.
(1)求false外接圆的标准方程.
(2)若点false是椭圆false第一象限上的点,直线false与false轴的交点为false,直线false与直线false的交点为false.若false与false的面积的比值为false,求直线false的方程.
选考题:共10分,请考生在22、23题中任选-题作答,如果多做则按所做的第题计分.
[选修4-4坐标系与参数方程]
22.在直角坐标系false中,曲线false的参数方程为:false(false为参数),以坐标原点false为极点,false轴的非负半轴为极轴建立极坐标系,曲线false的极坐标方程为false.
(1)求曲线false的极坐标方程和曲线false的直角坐标方程;
(2)在极坐标系中,射线falsefalse与曲线false交于点false,射线falsefalse与曲线false交于点false,求false的面积.
23.已知函数false.
(1)求不等式f(x)≤2的解集M;
(2)当x∈M时,false,求实数a的取值范围.
文科试题参考答案
1.B
【分析】
解出不等式false、false即可.
【详解】
由false可得false,由false可得false
所以“false”是“false”的必要而不充分条件
故选:B
2.C
【分析】
首先利用复数的乘法运算化简,之后根据纯虚数的定义列方程,解方程即可求得结果.
【详解】
false,
∵false为纯虚数,∴false.
故选:C.
3.B
【分析】
根据分层抽样的方法,列出方程,即可求解.
【详解】
根据分层抽样的方法,可得选《西游记》的学生抽取的人数为false.
故选:B.
4.C
【分析】
分别按照甲说了实话,乙说了实话和丙说了实话分类讨论,结合题意可得答案.
【详解】
①若甲说了实话,则丙也说了实话,不合题意;②若乙说了实话,则甲、丙都说了假话,符合题意;③若丙说了实话,则甲也说了实话,不合题意.由上知打破玻璃的是丙.
故选:C
【点睛】
本题考查推理与证明,考查分类讨论思想,属于基础题.
5.A
【分析】
依次模拟程序运行,直到满足条件,跳出循环即可.
【详解】
false
false
false
false,结束循环
故输出false的结果为18
故选:A
6.A
【分析】
利用树图列举基本事件总数,再找出第一张卡片上的数大于第二张卡片上的数的事件数,代入古典概型的公式求解.
【详解】
从5张卡片中随机抽取1张,放回后再随机抽取1张的情况如图:
基本事件总数为25,
第一张卡片上的数大于第二张卡片上的数的事件数为10,
故所求概率false.
故选:A.
7.B
【分析】
观察茎叶图中的数据,得出甲、乙两组数据的分布特征,从而判断它们的平均数和方差的大小.
【详解】
观察茎叶图中的数据知,
甲组数据主要集中在false之间,且成单峰分布,比较集中些;
乙组数据主要分布在false之间,相对分散些;
由此知平均数false,方差false.
故选:B.
【点睛】
本题考查了利用茎叶图中的数据判断平均数与方差大小的应用问题,是基础题.
8.C
【分析】
由不等式组false中实数对false对应的平面区域,分析两数false、false能与1构成钝角三角形三边的数对false对应的区域面积,利用几何概型公式列式求得false的解析式.
【详解】
根据题意知,false名同学取false对都小于false的正实数对false,即false,
对应区域为边长为1的正方形,其面积为1,
若两个正实数false、false能与1构成钝角三角形三边,则有false,
对应区域为阴影部分,其面积false;
则有false,解得false.
故选:C.
【点睛】
方法点睛:解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误 ;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.
9.B
【分析】
先由正弦定理,根据题中条件,求出false;再由三角形面积公式,求出false,利用余弦定理,即可求出结果.
【详解】
由正弦定理,可将false化为false,
因为false为三角形内角,所以false,因此false,
所以false,解得false,又false,所以false;
又false的面积为false,所以false,则false;
又false,所以由余弦定理可得:false,
所以false.
故选:B.
10.C
【分析】
设false内切圆的半径为false,可将所求面积之差表示为false,由内切圆圆心坐标可得false,根据过圆外一点作圆的切线,切线长相等的性质可将false表示为false,结合双曲线定义可构造方程求得false,由此可求得结果.
【详解】
设false内切圆的半径为false,则false,false,
falsefalse.
过点false作false于点false,false于点false,false于点false,
则由false的内切圆圆心为false知:false,false,false,false,
falsefalse,解得:false,
false.
故选:C.
【点睛】
关键点点睛:本题考查与双曲线焦点三角形有关的问题的求解,解题关键是能够利用过圆外一点作圆的切线,切线长相等的性质,结合双曲线的定义构造方程求得false.
11.B
【分析】
由回归直线恒过样本中心点,不一定经过每一个点,可判断①;由相关系数的绝对值趋近于1,相关性越强,可判断②;由方差的性质可判断③;由线性回归直线方程的特点可判断④;相关指数R2的大小,可判断⑤;由的随机变量K2的观测值k的大小可判断⑥;残差平方和越小,模型的拟合效果越好,可判断⑦.
【详解】
对于①,回归直线false恒过样本点的中心(false),可以不过任一个样本点,故①错误;
对于②,两个变量相关性越强,则相关系数r的绝对值就越接近于1,故②错误;
对于③,将一组数据的每个数据都加一个相同的常数后,由方差的性质可得方差不变,故③正确;
对于④,在回归直线方程false2﹣0.5x中,当解释变量x每增加一个单位时,
预报变量false平均减少0.5个单位,故④正确;
对于⑤,在线性回归模型中,相关指数R2表示解释变量x对于预报变量y的贡献率,
R2越接近于1,表示回归效果越好,故⑤正确;
对于⑥,对分类变量X与Y,它们的随机变量K2的观测值k来说,k越大,
“X与Y有关系”的把握程度越大,故⑥错误;
对于⑦,可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故⑦正确.
其中正确个数为4.
故选B.
【点睛】
本题考查命题的真假判断,主要是线性回归直线的特点和线性相关性的强弱、样本数据的特征值和模型的拟合度,考查判断能力,属于基础题.
12.B
【分析】
依题意false,得false在false上单调递增,转化为false恒成立,则false,令false,利用false的单调性可得答案.
【详解】
依题意,得false,且false,
false,所以false,
则false在false上单调递增,则false,
false恒成立,则false,令false,则false,当false时false;当false时,false,
故false,所以false,
故选:B.
【点睛】
解题的关键点是含有参数的不等式恒成立的问题,可以进行参数分离,再构造函数,考查了学生分析问题、解决问题的能力.
13.800
【分析】
由图知,各段的频率可知,又由总人数为1000,及格人数即为总人数乘上60分以上的频率.
【详解】
解:由图知40到50,50到60的频率分别为0.05,0.15,
故不及格的频率是0.2,又学生总数为1000名,
所以不及格的有200人,及格有800人.
故答案为:800.
【点睛】
本题考查用样本频率分布估计总体分布,观察图形是关键,要注意纵坐标表示的是频率,还是频率false组距,是基础题.
14.40
【分析】
由表中数据,计算得false,false,代入回归直线方程中可求得答案.
【详解】
由表中数据,计算可得false,false,
因为回归直线方程false过样本中心点,所以有false,解得false.
故答案为:40.
15.2
【分析】
利用抛物线的定义转化false,再利用圆外的点和圆上的点连线的最小值,数形结合求false最小值.
【详解】
设抛物线的准线false,false于点false,则false,
圆外的点和圆上的点的连线的最小值是false,
所以false
由图可知,false的最小值是点false到准线false的距离false,
所以false最小值是false.
故答案为:2
【点睛】
结论点睛:本题考查抛物线与圆的几何性质有关的最值,涉及与圆有关的最值具体结论如下:
(1)设false为圆的圆心,半径为false,圆外一点false到圆上的距离的最小值为false,最大值为false;
(2)过圆内一点的最长弦为圆的直径,最短弦是以该点为中点的弦;
(3)记圆的半径为false,圆心到直线的距离为false,直线与圆相离,则圆上的点到直线的最大距离为false,最小值为false;
16.false
【解析】
试题分析:因为函数false与false是互为反函数,它们的图象关于直线false对称,因为false取最小值时点false到直线false的距离也是最小,false,令false,则false,false,因此有false,false,所以false最小值为falsefalse.
考点:两点间的距离公式,转化与化归思想.
【名师点睛】本题表面上考查两点间距离的最小值,实质考查转化与化归的数学思想,由于两点都在超越函数的图象上,直接求距离不易求得最值,解决这个问题我们用到两个转化,第一个转化是利用这两个函数图象关于直线false对称这个性质可把false的最小值转化为一个函数图象上的点到直线false的距离的最小值的2倍,第二个转化是求函数图象上点到直线false的距离的最小值时,把直线false平移到与函数图象相切时,切点到直线false的距离就是最小值,这样只要求得函数图象在哪个点处的切线与直线false平行.经过这样的转化后,问题就非常容易求得.
17.(1)false;(2)false.
【分析】
(1)根据等比数列的性质,结合等差数列的通项公式进行求解即可;
(2)根据等比数列的定义,结合等比数列、等差数列前false项和公式进行求解即可;
【详解】
(1)设等差数列false的公差为false,
所以有false,false,∵false,false,false成等比数列,∴false,即false∵false∴false,
又∵false,∴false,
即false,∴false;
(2)由题意知false,false,false,∴false是以4为首项4为公比的等比数列.记数列false得前false项和为false,则false,
数列false的前false项和false,
false.
18.(1)填表见解析;没有;(2)false.
【分析】
(1)由200×0.6=120以及表中数据即可完善列联表,计算观测值,再利用独立性检验的基本思想即可求解;
(2)记3名男生为false,false,false,2名女生为false,false,列举所有可能情况即可求得结果.
【详解】
解:(1)false在这200名学生中随机抽取1人,抽到喜欢数学竞赛的概率为0.6,
false喜欢数学竞赛的人数为false(人),
false不欢数学竞赛的人数为80人,
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
50
120
女生
50
30
80
合计
120
80
200
false,
false没有90%的把握认为喜欢数学竞赛与性别有关;
(2)记3名男生为false,false,false,2名女生为false,false,
则5人中抽取3人的所有可能情况为:false,false,false,false,(A,C,b),false,false,false,false,false,false,
共10种结果,其中3人中至少有一名女生的9种,
所以所求概率false.
19.(I)证明见解析;(II)false
【分析】
(I)根据直三棱柱及正三角形的性质,证得false平面false,从而证得false;
(II)四棱锥false是以直角梯形false作底,高的长度与EC相等,分别求得各棱长,代入椎体体积公式即可求得.
【详解】
(I)在直三棱柱false中,平面false平面false,且交线为AB,
又在false中,false,false平面false,
故false平面false,又false平面false,
故false
(II)由(I)知,四棱锥false是以直角梯形false作底,高的长度与EC相等,
其中false,
则四棱锥false的体积为false.
【点睛】
方法点睛:证明线线垂直,可以通过证明线面垂直,然后利用线垂直于面上的任一条线,从而证得.
20.(1)见解析;(2)证明见解析.
【分析】
(1)可求得false,分false与false两类讨论,可得false在false上单调情况;
(2)记函数false,通过求导后可得false在false上单调递增,依题意,可得即false,再由false,知false,于是可证得结论成立.
【详解】
解:(1)false的定义域为false,
false
当false时,false恒成立,所以,false在false上单调递增;
当false时,令false,得到false
所以当false时,false,false单调递增,
当false时,false,false单调递减.
综上所述:
当false时,false在false上单调递增;
当false时,false在false上单调递增,在false上单调递减.
(2)记函数false,则false
易知false在false上单调递增,
又由false,false知,false在false上有唯一的实数根false,
且false,则false,即false(*)
当false时,false,false单调递减;
当false时,false,false单调递增,
所以false,结合(*)式false,知false,
所以false
则false,即false,
所以有false恒成立.
【点睛】
方法点睛:利用导数证明不等式常见类型及解题策略(1) 构造差函数false.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.
21.(1)false;(2)false.
【分析】
(1)由椭圆方程求得false坐标,设false外接圆的圆心为false,求得圆心坐标和半径得方程;
(2)设false,false的纵坐标分别为false,false,false,false,写出直线false方程与椭圆方程联立求得false,再由直线相交求得false,然后利用面积比求得false,得直线方程.
【详解】
解:(1)易知false,false,false.
根据对称性可知false外接圆的圆心在false轴上,设为false,
连接false,则有false,即false,
解得false,
设false外接圆的半径为false,则false,
∴false外接圆的标准方程是false.
(2)设false,false的纵坐标分别为false,false,false,false,
则直线false的方程为false,①
与false联立,消去false,整理得false,
∴false.
易知直线false的方程为false,②
①②联立可得false.
由题易知false,∴false,从而false,
∴false,解得false或false(舍去).
此时直线false的方程为false,即false.
【点睛】
关键点点睛:本题解题关键在求解本题第(1)问时,发现三角形的特征是求解的关键;求解第(2)问时,能够根据题意确定出点false在点false的右侧是一个关键点,另外,能够将两个三角形的面积的比值转化为线段的长度的比值也是关键.
22.(1)false的极坐标方程为:false,false,false的直角坐标方程为:false;(2)false.
【分析】
(1)由曲线false的参数方程消去参数false可得false的普通方程,即可得出极坐标方程,再将false的极坐标方程化简可得出直角坐标方程;
(2)将false分别代入false和false的极坐标方程可求得false极坐标,即可求出面积.
【详解】
解:(1)由题意得:false,消去false,∴falsefalse
∴false即false
化简为:false,false
∴false的极坐标方程为:false,false,
由false得:false
∴false即:false
∴false的直角坐标方程为:false
(2)由false得:false,∴false,
由false得:false,∴false,
falsefalsefalse.
【点睛】
关键点睛:本题考查极坐标方程的化简与应用,解题的关键是正确理解极坐标的几何意义.
23.(1)false;(2)(0,1).
【分析】
(1)去掉绝对值号得false,分成false和false两种情况解不等式false.
(2)由(1)可得false,从而可得false,进而可求出实数a的取值范围.
【详解】
解:(1)false,当false时,false;
当false时,由false,得false.
综上所述,不等式false的解集M为false.
(2)由(1)得,当false时,false,那么false,从而可得false,
解得,false,即实数a的取值范围是(0,1).
24.(1)false;(2)false.
【分析】
(1)将false代入false,零点分段法去绝对值,分段求解最后求并集即可;(2)当false时,false恒成立,分情况讨论当false时和false时,false的正负,去绝对值,代入false判断false是否恒成立,从而求出false的范围.
【详解】
(1)当false时,false,
false等价于false或false或false解得false或false或false,
所以不等式false的解集为false;
(2)当false时,false,
false,且false,
当false时,false,
false,
false,
因为false,而false,所以false恒成立,所以false满足题意;
当false时,false当false,false,此时false不恒成立,故不满足题意;
综上,实数false的取值范围是false.
【点睛】
思路点睛:(1)解绝对值不等式常用的方法是零点分段法,去绝对值分段求解;(2)绝对值内含参数的绝对值不等式,常用分类讨论的方法去绝对值,再分情况讨论求解.
一、单选题,本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设false,则“false”是“false”的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件D.不充分也不必要条件
2.已知复数false,其中false若false为纯虚数,则( )
A.false B.false C.false D.false
3.某校初一有500名学生,为了培养学生良好的阅读习惯,学校要求他们从四大名著中选一本阅读,其中有200人选《三国演义》,125人选《水浒传》,125人选《西游记》,50人选《红楼梦》,若采用分层抽样的方法随机抽取40名学生分享他们的读后感,则选《西游记》的学生抽取的人数为( )
A.5 B.10 C.12 D.15
4.三个学生在校园内踢足球,“砰”的一声,不知道是谁踢的球把教室窗户的玻璃打破了,老师跑过来一看,问:“是谁打破了玻璃窗户”.甲说:“是乙打破的”;乙说:“是丙打破的”;丙说:“是乙打破的”,如果这三个孩子中只有一个人说了实话,则打破玻璃窗户的是( )
A.甲 B.乙 C.丙 D.不能确定
5.执行如图所示的程序框图,若输入false,则输出false的结果为( )
A.18 B.14 C.20 D.22
6.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为( )
A.false B.false C.false D.false
7.某学校为了解传统教学和教改实验的课堂教学情况,选取20.人平均分成同样水平的两组(甲组采用教改实验教学,乙组采用传统教学),一学期以后根据他们的期末成绩绘制茎叶图,如图所示,则( )
A.false,false B.false,false
C.false,false D.false,false
8.关于圆周率false,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计false的值:先请全校false名同学每人随机写下一个都小于1的正实数对false;再统计两数能与1构成钝角三角形三边的数对false的个数false;最后再根据统计数false估计false的值,那么可以估计false的值约为( )
A.false B.false C.false D.false
9.已知false的内角false的对边分别为false且falsefalse,false的面积为false则false( )
A.false B.5 C.8 D.false
10.设双曲线false的左、右焦点分别false、false,点false为双曲线右支上一点,false的内切圆圆心为false,则false的面积与false的面积之差为( )
A.false B.false C.false D.false
11.已知下列命题:
①回归直线false恒过样本点的中心false,且至少过一个样本点;
②两个变量相关性越强,则相关系数r就越接近于1;
③将一组数据的每个数据都加一个相同的常数后,方差不变;
④在回归直线方程false 中,当解释变量x增加一个单位时,预报变量false平均减少0.5;
⑤在线性回归模型中,相关指数false表示解释变量false对于预报变量false的贡献率,false越接近于1,表示回归效果越好;
⑥对分类变量false与false,它们的随机变量false的观测值false来说, false越小,“false与false有关系”的把握程度越大.
⑦两个模型中残差平方和越小的模型拟合的效果越好.
则正确命题的个数是( )
A.3 B.4 C.5 D.6
12.已知false,对false,且false,恒有false,则实数false的取值范围是( )
A.false B.false C.false D.false
二、填空题,本题共4小题,每小题5分,共20分.
13.统计某校1000名学生的数学会考成绩,得到样本频率分布直方图如图所示,规定不低于60分为及格,则及格人数是_________________.
14.上饶市婺源县被誉为“茶乡”,婺源茶业千年不衰,新时代更是方兴未艾,其中由农业部监制的婺源大山顶特供茶“擂鼓峰茶尤为出名,为了解每壶“擂鼓峰”茶中所放茶叶量false克与食客的满意率false的关系,抽样得一组数据如下表:
false(克)
2
4
5
6
8
false(%)
30
false
50
70
60
根据表中的全部数据,用最小二乘法得出false与false的线性回归方程为false,则表中false的值为________.
15.F为抛物线false的焦点,点P在抛物线上,Q是圆false上的点,则false最小值是__________.
16.已知点false在曲线false(false是自然对数的底数)上,点false在曲线false上,则false的最小值为________.
三、解答题
17.已知公差不为0的等差数列false的前false项和为false,且false,false,false,false成等比数列.
(1)求数列false的通项公式;
(2)若数列false满足false,求数列false的前false项和false.
18.为进一步提升学生学习数学的热情,学校举行了数学学科知识竞赛.为了解学生对数学竞赛的喜爱程度是否与性别有关,现对高中部200名学生进行了问卷调查,得到如下2×2列联表:
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
女生
30
合计
已知在这200名学生中随机抽取1人,抽到喜欢数学竞赛的概率为0.6.
(1)将2×2列联表补充完整,并判断是否有90%的把握认为喜欢数学竞赛与性别有关?
(2)从上述不喜欢数学竞赛的学生中男生抽取3人,女生抽取2人,再在这5人中抽取3人,调查其喜欢的活动类型,求抽取的3人中至少有一名女生的概率.
参考公式及数据:false.
P(K2≥k)
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.01
0.005
0.001
k
0.46
0.71
1.32
2.07
2.71
3.84
5.024
6.635
7.879
10.828
19.如图,在直三棱柱false中,底面false是边长为3的等边三角形,false,false是false的中点.
(Ⅰ)证明:false;
(Ⅱ)求四棱锥false的体积.
20.已知函数false.
(1)讨论函数false的单调性;
(2)证明:函数false(false为自然对数的底数)恒成立.
21.已知椭圆false:false的右顶点为false,上?下顶点分别是false,false.
(1)求false外接圆的标准方程.
(2)若点false是椭圆false第一象限上的点,直线false与false轴的交点为false,直线false与直线false的交点为false.若false与false的面积的比值为false,求直线false的方程.
选考题:共10分,请考生在22、23题中任选-题作答,如果多做则按所做的第题计分.
[选修4-4坐标系与参数方程]
22.在直角坐标系false中,曲线false的参数方程为:false(false为参数),以坐标原点false为极点,false轴的非负半轴为极轴建立极坐标系,曲线false的极坐标方程为false.
(1)求曲线false的极坐标方程和曲线false的直角坐标方程;
(2)在极坐标系中,射线falsefalse与曲线false交于点false,射线falsefalse与曲线false交于点false,求false的面积.
23.已知函数false.
(1)求不等式f(x)≤2的解集M;
(2)当x∈M时,false,求实数a的取值范围.
文科试题参考答案
1.B
【分析】
解出不等式false、false即可.
【详解】
由false可得false,由false可得false
所以“false”是“false”的必要而不充分条件
故选:B
2.C
【分析】
首先利用复数的乘法运算化简,之后根据纯虚数的定义列方程,解方程即可求得结果.
【详解】
false,
∵false为纯虚数,∴false.
故选:C.
3.B
【分析】
根据分层抽样的方法,列出方程,即可求解.
【详解】
根据分层抽样的方法,可得选《西游记》的学生抽取的人数为false.
故选:B.
4.C
【分析】
分别按照甲说了实话,乙说了实话和丙说了实话分类讨论,结合题意可得答案.
【详解】
①若甲说了实话,则丙也说了实话,不合题意;②若乙说了实话,则甲、丙都说了假话,符合题意;③若丙说了实话,则甲也说了实话,不合题意.由上知打破玻璃的是丙.
故选:C
【点睛】
本题考查推理与证明,考查分类讨论思想,属于基础题.
5.A
【分析】
依次模拟程序运行,直到满足条件,跳出循环即可.
【详解】
false
false
false
false,结束循环
故输出false的结果为18
故选:A
6.A
【分析】
利用树图列举基本事件总数,再找出第一张卡片上的数大于第二张卡片上的数的事件数,代入古典概型的公式求解.
【详解】
从5张卡片中随机抽取1张,放回后再随机抽取1张的情况如图:
基本事件总数为25,
第一张卡片上的数大于第二张卡片上的数的事件数为10,
故所求概率false.
故选:A.
7.B
【分析】
观察茎叶图中的数据,得出甲、乙两组数据的分布特征,从而判断它们的平均数和方差的大小.
【详解】
观察茎叶图中的数据知,
甲组数据主要集中在false之间,且成单峰分布,比较集中些;
乙组数据主要分布在false之间,相对分散些;
由此知平均数false,方差false.
故选:B.
【点睛】
本题考查了利用茎叶图中的数据判断平均数与方差大小的应用问题,是基础题.
8.C
【分析】
由不等式组false中实数对false对应的平面区域,分析两数false、false能与1构成钝角三角形三边的数对false对应的区域面积,利用几何概型公式列式求得false的解析式.
【详解】
根据题意知,false名同学取false对都小于false的正实数对false,即false,
对应区域为边长为1的正方形,其面积为1,
若两个正实数false、false能与1构成钝角三角形三边,则有false,
对应区域为阴影部分,其面积false;
则有false,解得false.
故选:C.
【点睛】
方法点睛:解决几何概型问题常见类型有:长度型、角度型、面积型、体积型,求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积;几何概型问题还有以下几点容易造成失分,在备考时要高度关注:(1)不能正确判断事件是古典概型还是几何概型导致错误;(2)基本事件对应的区域测度把握不准导致错误 ;(3)利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.
9.B
【分析】
先由正弦定理,根据题中条件,求出false;再由三角形面积公式,求出false,利用余弦定理,即可求出结果.
【详解】
由正弦定理,可将false化为false,
因为false为三角形内角,所以false,因此false,
所以false,解得false,又false,所以false;
又false的面积为false,所以false,则false;
又false,所以由余弦定理可得:false,
所以false.
故选:B.
10.C
【分析】
设false内切圆的半径为false,可将所求面积之差表示为false,由内切圆圆心坐标可得false,根据过圆外一点作圆的切线,切线长相等的性质可将false表示为false,结合双曲线定义可构造方程求得false,由此可求得结果.
【详解】
设false内切圆的半径为false,则false,false,
falsefalse.
过点false作false于点false,false于点false,false于点false,
则由false的内切圆圆心为false知:false,false,false,false,
falsefalse,解得:false,
false.
故选:C.
【点睛】
关键点点睛:本题考查与双曲线焦点三角形有关的问题的求解,解题关键是能够利用过圆外一点作圆的切线,切线长相等的性质,结合双曲线的定义构造方程求得false.
11.B
【分析】
由回归直线恒过样本中心点,不一定经过每一个点,可判断①;由相关系数的绝对值趋近于1,相关性越强,可判断②;由方差的性质可判断③;由线性回归直线方程的特点可判断④;相关指数R2的大小,可判断⑤;由的随机变量K2的观测值k的大小可判断⑥;残差平方和越小,模型的拟合效果越好,可判断⑦.
【详解】
对于①,回归直线false恒过样本点的中心(false),可以不过任一个样本点,故①错误;
对于②,两个变量相关性越强,则相关系数r的绝对值就越接近于1,故②错误;
对于③,将一组数据的每个数据都加一个相同的常数后,由方差的性质可得方差不变,故③正确;
对于④,在回归直线方程false2﹣0.5x中,当解释变量x每增加一个单位时,
预报变量false平均减少0.5个单位,故④正确;
对于⑤,在线性回归模型中,相关指数R2表示解释变量x对于预报变量y的贡献率,
R2越接近于1,表示回归效果越好,故⑤正确;
对于⑥,对分类变量X与Y,它们的随机变量K2的观测值k来说,k越大,
“X与Y有关系”的把握程度越大,故⑥错误;
对于⑦,可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故⑦正确.
其中正确个数为4.
故选B.
【点睛】
本题考查命题的真假判断,主要是线性回归直线的特点和线性相关性的强弱、样本数据的特征值和模型的拟合度,考查判断能力,属于基础题.
12.B
【分析】
依题意false,得false在false上单调递增,转化为false恒成立,则false,令false,利用false的单调性可得答案.
【详解】
依题意,得false,且false,
false,所以false,
则false在false上单调递增,则false,
false恒成立,则false,令false,则false,当false时false;当false时,false,
故false,所以false,
故选:B.
【点睛】
解题的关键点是含有参数的不等式恒成立的问题,可以进行参数分离,再构造函数,考查了学生分析问题、解决问题的能力.
13.800
【分析】
由图知,各段的频率可知,又由总人数为1000,及格人数即为总人数乘上60分以上的频率.
【详解】
解:由图知40到50,50到60的频率分别为0.05,0.15,
故不及格的频率是0.2,又学生总数为1000名,
所以不及格的有200人,及格有800人.
故答案为:800.
【点睛】
本题考查用样本频率分布估计总体分布,观察图形是关键,要注意纵坐标表示的是频率,还是频率false组距,是基础题.
14.40
【分析】
由表中数据,计算得false,false,代入回归直线方程中可求得答案.
【详解】
由表中数据,计算可得false,false,
因为回归直线方程false过样本中心点,所以有false,解得false.
故答案为:40.
15.2
【分析】
利用抛物线的定义转化false,再利用圆外的点和圆上的点连线的最小值,数形结合求false最小值.
【详解】
设抛物线的准线false,false于点false,则false,
圆外的点和圆上的点的连线的最小值是false,
所以false
由图可知,false的最小值是点false到准线false的距离false,
所以false最小值是false.
故答案为:2
【点睛】
结论点睛:本题考查抛物线与圆的几何性质有关的最值,涉及与圆有关的最值具体结论如下:
(1)设false为圆的圆心,半径为false,圆外一点false到圆上的距离的最小值为false,最大值为false;
(2)过圆内一点的最长弦为圆的直径,最短弦是以该点为中点的弦;
(3)记圆的半径为false,圆心到直线的距离为false,直线与圆相离,则圆上的点到直线的最大距离为false,最小值为false;
16.false
【解析】
试题分析:因为函数false与false是互为反函数,它们的图象关于直线false对称,因为false取最小值时点false到直线false的距离也是最小,false,令false,则false,false,因此有false,false,所以false最小值为falsefalse.
考点:两点间的距离公式,转化与化归思想.
【名师点睛】本题表面上考查两点间距离的最小值,实质考查转化与化归的数学思想,由于两点都在超越函数的图象上,直接求距离不易求得最值,解决这个问题我们用到两个转化,第一个转化是利用这两个函数图象关于直线false对称这个性质可把false的最小值转化为一个函数图象上的点到直线false的距离的最小值的2倍,第二个转化是求函数图象上点到直线false的距离的最小值时,把直线false平移到与函数图象相切时,切点到直线false的距离就是最小值,这样只要求得函数图象在哪个点处的切线与直线false平行.经过这样的转化后,问题就非常容易求得.
17.(1)false;(2)false.
【分析】
(1)根据等比数列的性质,结合等差数列的通项公式进行求解即可;
(2)根据等比数列的定义,结合等比数列、等差数列前false项和公式进行求解即可;
【详解】
(1)设等差数列false的公差为false,
所以有false,false,∵false,false,false成等比数列,∴false,即false∵false∴false,
又∵false,∴false,
即false,∴false;
(2)由题意知false,false,false,∴false是以4为首项4为公比的等比数列.记数列false得前false项和为false,则false,
数列false的前false项和false,
false.
18.(1)填表见解析;没有;(2)false.
【分析】
(1)由200×0.6=120以及表中数据即可完善列联表,计算观测值,再利用独立性检验的基本思想即可求解;
(2)记3名男生为false,false,false,2名女生为false,false,列举所有可能情况即可求得结果.
【详解】
解:(1)false在这200名学生中随机抽取1人,抽到喜欢数学竞赛的概率为0.6,
false喜欢数学竞赛的人数为false(人),
false不欢数学竞赛的人数为80人,
喜欢数学竞赛
不喜欢数学竞赛
合计
男生
70
50
120
女生
50
30
80
合计
120
80
200
false,
false没有90%的把握认为喜欢数学竞赛与性别有关;
(2)记3名男生为false,false,false,2名女生为false,false,
则5人中抽取3人的所有可能情况为:false,false,false,false,(A,C,b),false,false,false,false,false,false,
共10种结果,其中3人中至少有一名女生的9种,
所以所求概率false.
19.(I)证明见解析;(II)false
【分析】
(I)根据直三棱柱及正三角形的性质,证得false平面false,从而证得false;
(II)四棱锥false是以直角梯形false作底,高的长度与EC相等,分别求得各棱长,代入椎体体积公式即可求得.
【详解】
(I)在直三棱柱false中,平面false平面false,且交线为AB,
又在false中,false,false平面false,
故false平面false,又false平面false,
故false
(II)由(I)知,四棱锥false是以直角梯形false作底,高的长度与EC相等,
其中false,
则四棱锥false的体积为false.
【点睛】
方法点睛:证明线线垂直,可以通过证明线面垂直,然后利用线垂直于面上的任一条线,从而证得.
20.(1)见解析;(2)证明见解析.
【分析】
(1)可求得false,分false与false两类讨论,可得false在false上单调情况;
(2)记函数false,通过求导后可得false在false上单调递增,依题意,可得即false,再由false,知false,于是可证得结论成立.
【详解】
解:(1)false的定义域为false,
false
当false时,false恒成立,所以,false在false上单调递增;
当false时,令false,得到false
所以当false时,false,false单调递增,
当false时,false,false单调递减.
综上所述:
当false时,false在false上单调递增;
当false时,false在false上单调递增,在false上单调递减.
(2)记函数false,则false
易知false在false上单调递增,
又由false,false知,false在false上有唯一的实数根false,
且false,则false,即false(*)
当false时,false,false单调递减;
当false时,false,false单调递增,
所以false,结合(*)式false,知false,
所以false
则false,即false,
所以有false恒成立.
【点睛】
方法点睛:利用导数证明不等式常见类型及解题策略(1) 构造差函数false.根据差函数导函数符号,确定差函数单调性,利用单调性得不等量关系,进而证明不等式.(2)根据条件,寻找目标函数.一般思路为利用条件将求和问题转化为对应项之间大小关系,或利用放缩、等量代换将多元函数转化为一元函数.
21.(1)false;(2)false.
【分析】
(1)由椭圆方程求得false坐标,设false外接圆的圆心为false,求得圆心坐标和半径得方程;
(2)设false,false的纵坐标分别为false,false,false,false,写出直线false方程与椭圆方程联立求得false,再由直线相交求得false,然后利用面积比求得false,得直线方程.
【详解】
解:(1)易知false,false,false.
根据对称性可知false外接圆的圆心在false轴上,设为false,
连接false,则有false,即false,
解得false,
设false外接圆的半径为false,则false,
∴false外接圆的标准方程是false.
(2)设false,false的纵坐标分别为false,false,false,false,
则直线false的方程为false,①
与false联立,消去false,整理得false,
∴false.
易知直线false的方程为false,②
①②联立可得false.
由题易知false,∴false,从而false,
∴false,解得false或false(舍去).
此时直线false的方程为false,即false.
【点睛】
关键点点睛:本题解题关键在求解本题第(1)问时,发现三角形的特征是求解的关键;求解第(2)问时,能够根据题意确定出点false在点false的右侧是一个关键点,另外,能够将两个三角形的面积的比值转化为线段的长度的比值也是关键.
22.(1)false的极坐标方程为:false,false,false的直角坐标方程为:false;(2)false.
【分析】
(1)由曲线false的参数方程消去参数false可得false的普通方程,即可得出极坐标方程,再将false的极坐标方程化简可得出直角坐标方程;
(2)将false分别代入false和false的极坐标方程可求得false极坐标,即可求出面积.
【详解】
解:(1)由题意得:false,消去false,∴falsefalse
∴false即false
化简为:false,false
∴false的极坐标方程为:false,false,
由false得:false
∴false即:false
∴false的直角坐标方程为:false
(2)由false得:false,∴false,
由false得:false,∴false,
falsefalsefalse.
【点睛】
关键点睛:本题考查极坐标方程的化简与应用,解题的关键是正确理解极坐标的几何意义.
23.(1)false;(2)(0,1).
【分析】
(1)去掉绝对值号得false,分成false和false两种情况解不等式false.
(2)由(1)可得false,从而可得false,进而可求出实数a的取值范围.
【详解】
解:(1)false,当false时,false;
当false时,由false,得false.
综上所述,不等式false的解集M为false.
(2)由(1)得,当false时,false,那么false,从而可得false,
解得,false,即实数a的取值范围是(0,1).
24.(1)false;(2)false.
【分析】
(1)将false代入false,零点分段法去绝对值,分段求解最后求并集即可;(2)当false时,false恒成立,分情况讨论当false时和false时,false的正负,去绝对值,代入false判断false是否恒成立,从而求出false的范围.
【详解】
(1)当false时,false,
false等价于false或false或false解得false或false或false,
所以不等式false的解集为false;
(2)当false时,false,
false,且false,
当false时,false,
false,
false,
因为false,而false,所以false恒成立,所以false满足题意;
当false时,false当false,false,此时false不恒成立,故不满足题意;
综上,实数false的取值范围是false.
【点睛】
思路点睛:(1)解绝对值不等式常用的方法是零点分段法,去绝对值分段求解;(2)绝对值内含参数的绝对值不等式,常用分类讨论的方法去绝对值,再分情况讨论求解.
同课章节目录
