1.2.1函数的概念 人教版A高一数学必修1(共21张PPT)
文档属性
| 名称 | 1.2.1函数的概念 人教版A高一数学必修1(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 856.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
1.2.1
函数的概念(1)
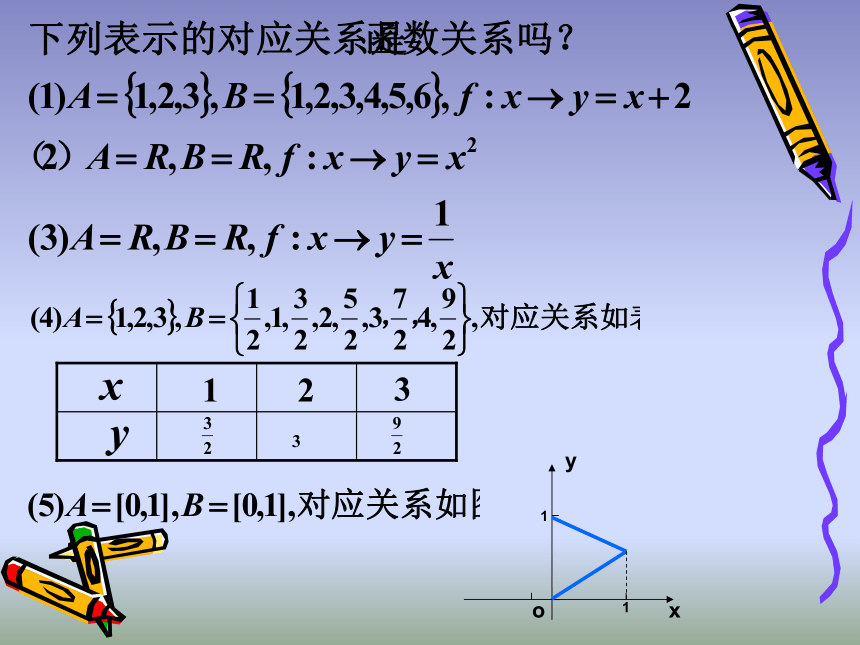
1.在初中我们学过哪些函数?
2.分析归纳:以上三个实例,它们有什么共同点?
阅读课本P15-16
设A,B是非空的数集,如果按照某种确定的对应关系f,
对于A中的任何一个数x,在集合B中都有唯一确定的数f(x)与它对应,
那么就称f:A
B为从集合A到集合B的一个函数,
记作
y=f(x),x∈A.
此时,x叫做自变量,
集合A叫做函数的定义域;
函数值的集合{f(x)|x∈A}叫做函数的值域。
思考:B是值域吗?
与x的值相对应的y值叫做函数值;
x
y
o
1
1
2.函数
的定义域是
;
如:
1.函数y=-2x+1的定义域是
;
3.函数
的定义域是
。
R
{x|x≠0}
{x|x≥1}
若未加以特别说明,函数的定义域是指使这个函数有意义的全体实数构成的集合。
练习:1.二次函数
的定义域是__
,值域是_________。
2.请用函数定义描述这个函数。
答:对于R中的任意一个数x,在B中都有
唯一的数y=ax2+bx+c(a≠0)和它对应。
R
x
y
o
2
2
(1)
x
o
2
2
y
(3)
x
y
o
-1
3
(4)
x
y
o
1
2
3
2
4
(5)
x
y
o
1
2
3
2
4
(6)
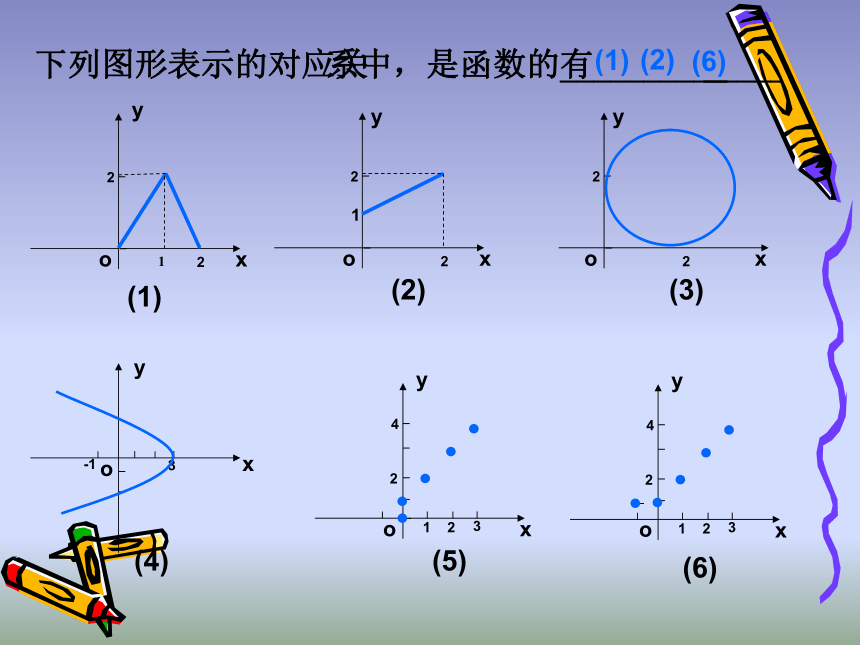
(1)
(2)
(6)
x
o
2
2
y
(2)
1
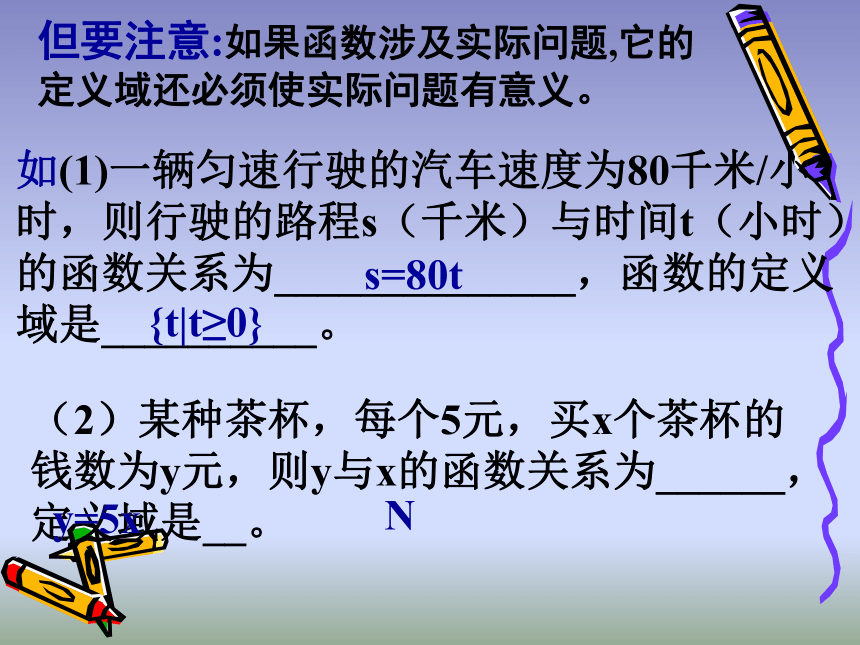
但要注意:如果函数涉及实际问题,它的定义域还必须使实际问题有意义。
如(1)一辆匀速行驶的汽车速度为80千米/小时,则行驶的路程s(千米)与时间t(小时)的函数关系为______________,函数的定义域是__________。
(2)某种茶杯,每个5元,买x个茶杯的钱数为y元,则y与x的函数关系为______,定义域是__。
s=80t
{t|t≥0}
y=5x
N
(3)下表记录了几个不同气压下水的沸点。
气压/(105Pa)
0.5
1.0
2.0
5.0
10
沸点/(°C)
81
100
121
152
179
这张表给出了沸点与气压之间的函数关系。
定义域是
{0.5,
1.0,
2.0,
5.0,
10}
设a,b是两个实数,且a定义
名称
符号
几何表示
{x|a≤x≤b}
闭区间
[a,b]
{x|a开区间
(a,b)
{x|a≤x左闭右开区间
[a,b)
{x|a左开右闭区间
(a,b]
a
b
a
b
a
b
a
b
1.这里实数a,b都叫做区间的端点。
2.实数集R也可以用区间表示为(-∞,+∞)。
“∞”读作“无穷大”,
“+∞”读作“正无穷大”,
“-∞”读作“负无穷大”,
用区间表示下列集合:
(1){x|x≥a}=______;
(2){x|x>a}=_______;
(3){x|x≤b}=______;
(4){x|x[a,+∞)
(a,+∞)
(-∞,b]
(-∞,b)
用区间表示下列集合:
(5)函数y=2x+5的定义域__________;
(6)不等式1<2x-1≤3的解集________;
(7){x∈R|
}=__________;
(8){y∈R|y=-x2}=_________;
(-∞,+∞)
(1,2]
(-∞,0]
[2,+∞)
对函数y=f(x)的理解:
(1)f(x)是一个函数符号,表示“y是x的函数”;
绝对不能理解为“y等于f与x的乘积。”在不同的函数中,f的具体含义不一样。在研究函数时,除用符号f(x)表示外,还常用g(x)等符号来表示。
(2)定义域是自变量x的取值范围;
(3)f(a)表示函数f(x)当自变量x=a时的函数值。
如:f(x)=x2+2x,
则f(1)=
例1:已知函数f(x)=
(1)函数的定义域;
(2)f(-2)、
f(0)、
f(
);
(3)若a>0,求f(a)、
f(a-1)。
1.函数的三要素:
定义域、对应关系、值域。
在大多数情况下,一旦定义域和对应关系确定,函数的值域也随之确定。
2.两个函数相等:
由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域相同,并且对应关系完全一致,则称这两个函数相等。
定义域不同而对应关系相同的函数,应看作两个不相同的函数。
如y=x2(x∈R)和
y=x2(x﹥0)是两个不相同的函数
。
例2:判断下列哪个函数与y=x是相等函数?
(
)
C
点评:只有定义域和对应法则都完全相同的函数才是相同的函数。
练习:判断下列函数
与
是否表示同一个函数,说明理由?
f(x)=3是函数吗?若是请说出函数的三要素。
是;
定义域是R,
值域是{3};
对应关系是f(x)=3。
练习:课本P19
(1)函数的概念及三要素;
(2)对函数y=f(x)的理解;
(3)区间的概念。
作业:
课本P24:1,2,3,4
1.2.1
函数的概念(1)
1.在初中我们学过哪些函数?
2.分析归纳:以上三个实例,它们有什么共同点?
阅读课本P15-16
设A,B是非空的数集,如果按照某种确定的对应关系f,
对于A中的任何一个数x,在集合B中都有唯一确定的数f(x)与它对应,
那么就称f:A
B为从集合A到集合B的一个函数,
记作
y=f(x),x∈A.
此时,x叫做自变量,
集合A叫做函数的定义域;
函数值的集合{f(x)|x∈A}叫做函数的值域。
思考:B是值域吗?
与x的值相对应的y值叫做函数值;
x
y
o
1
1
2.函数
的定义域是
;
如:
1.函数y=-2x+1的定义域是
;
3.函数
的定义域是
。
R
{x|x≠0}
{x|x≥1}
若未加以特别说明,函数的定义域是指使这个函数有意义的全体实数构成的集合。
练习:1.二次函数
的定义域是__
,值域是_________。
2.请用函数定义描述这个函数。
答:对于R中的任意一个数x,在B中都有
唯一的数y=ax2+bx+c(a≠0)和它对应。
R
x
y
o
2
2
(1)
x
o
2
2
y
(3)
x
y
o
-1
3
(4)
x
y
o
1
2
3
2
4
(5)
x
y
o
1
2
3
2
4
(6)
(1)
(2)
(6)
x
o
2
2
y
(2)
1
但要注意:如果函数涉及实际问题,它的定义域还必须使实际问题有意义。
如(1)一辆匀速行驶的汽车速度为80千米/小时,则行驶的路程s(千米)与时间t(小时)的函数关系为______________,函数的定义域是__________。
(2)某种茶杯,每个5元,买x个茶杯的钱数为y元,则y与x的函数关系为______,定义域是__。
s=80t
{t|t≥0}
y=5x
N
(3)下表记录了几个不同气压下水的沸点。
气压/(105Pa)
0.5
1.0
2.0
5.0
10
沸点/(°C)
81
100
121
152
179
这张表给出了沸点与气压之间的函数关系。
定义域是
{0.5,
1.0,
2.0,
5.0,
10}
设a,b是两个实数,且a
名称
符号
几何表示
{x|a≤x≤b}
闭区间
[a,b]
{x|a
(a,b)
{x|a≤x
[a,b)
{x|a
(a,b]
a
b
a
b
a
b
a
b
1.这里实数a,b都叫做区间的端点。
2.实数集R也可以用区间表示为(-∞,+∞)。
“∞”读作“无穷大”,
“+∞”读作“正无穷大”,
“-∞”读作“负无穷大”,
用区间表示下列集合:
(1){x|x≥a}=______;
(2){x|x>a}=_______;
(3){x|x≤b}=______;
(4){x|x
(a,+∞)
(-∞,b]
(-∞,b)
用区间表示下列集合:
(5)函数y=2x+5的定义域__________;
(6)不等式1<2x-1≤3的解集________;
(7){x∈R|
}=__________;
(8){y∈R|y=-x2}=_________;
(-∞,+∞)
(1,2]
(-∞,0]
[2,+∞)
对函数y=f(x)的理解:
(1)f(x)是一个函数符号,表示“y是x的函数”;
绝对不能理解为“y等于f与x的乘积。”在不同的函数中,f的具体含义不一样。在研究函数时,除用符号f(x)表示外,还常用g(x)等符号来表示。
(2)定义域是自变量x的取值范围;
(3)f(a)表示函数f(x)当自变量x=a时的函数值。
如:f(x)=x2+2x,
则f(1)=
例1:已知函数f(x)=
(1)函数的定义域;
(2)f(-2)、
f(0)、
f(
);
(3)若a>0,求f(a)、
f(a-1)。
1.函数的三要素:
定义域、对应关系、值域。
在大多数情况下,一旦定义域和对应关系确定,函数的值域也随之确定。
2.两个函数相等:
由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域相同,并且对应关系完全一致,则称这两个函数相等。
定义域不同而对应关系相同的函数,应看作两个不相同的函数。
如y=x2(x∈R)和
y=x2(x﹥0)是两个不相同的函数
。
例2:判断下列哪个函数与y=x是相等函数?
(
)
C
点评:只有定义域和对应法则都完全相同的函数才是相同的函数。
练习:判断下列函数
与
是否表示同一个函数,说明理由?
f(x)=3是函数吗?若是请说出函数的三要素。
是;
定义域是R,
值域是{3};
对应关系是f(x)=3。
练习:课本P19
(1)函数的概念及三要素;
(2)对函数y=f(x)的理解;
(3)区间的概念。
作业:
课本P24:1,2,3,4
