2020-2021学年湘教版八年级下册数学期末冲刺试题(Word版,附答案解析)
文档属性
| 名称 | 2020-2021学年湘教版八年级下册数学期末冲刺试题(Word版,附答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 263.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 23:56:21 | ||
图片预览



文档简介
2020-2021学年湘教新版八年级下册数学期末冲刺试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组数中能作为直角三角形的三边长的是( )
A.1,2,3
B.,,
C.4,5,
D.6,8,12
2.从六边形的一个顶点出发,可引出的对角线共有( )
A.1条
B.2条
C.3条
D.4条
3.下列图案中是中心对称图形但不是轴对称图形的是( )
A.
B.
C.
D.
4.已知点P(a﹣3,a+2)在x轴上,则a=( )
A.﹣2
B.3
C.﹣5
D.5
5.已知直线y=kx+b经过第一、二、四象限,那么直线y=bx+k一定不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.在?ABCD中,AD=13,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=3,则AB的长( )
A.8
B.5
C.3或5
D.5或8
7.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB恰好过点(6,2),则直线AB的表达式为( )
A.y=2x﹣10
B.y=﹣2x+14
C.y=2x+2
D.y=﹣x+5
8.下列命题是真命题的个数为( )
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是180°.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2
B.3
C.4
D.5
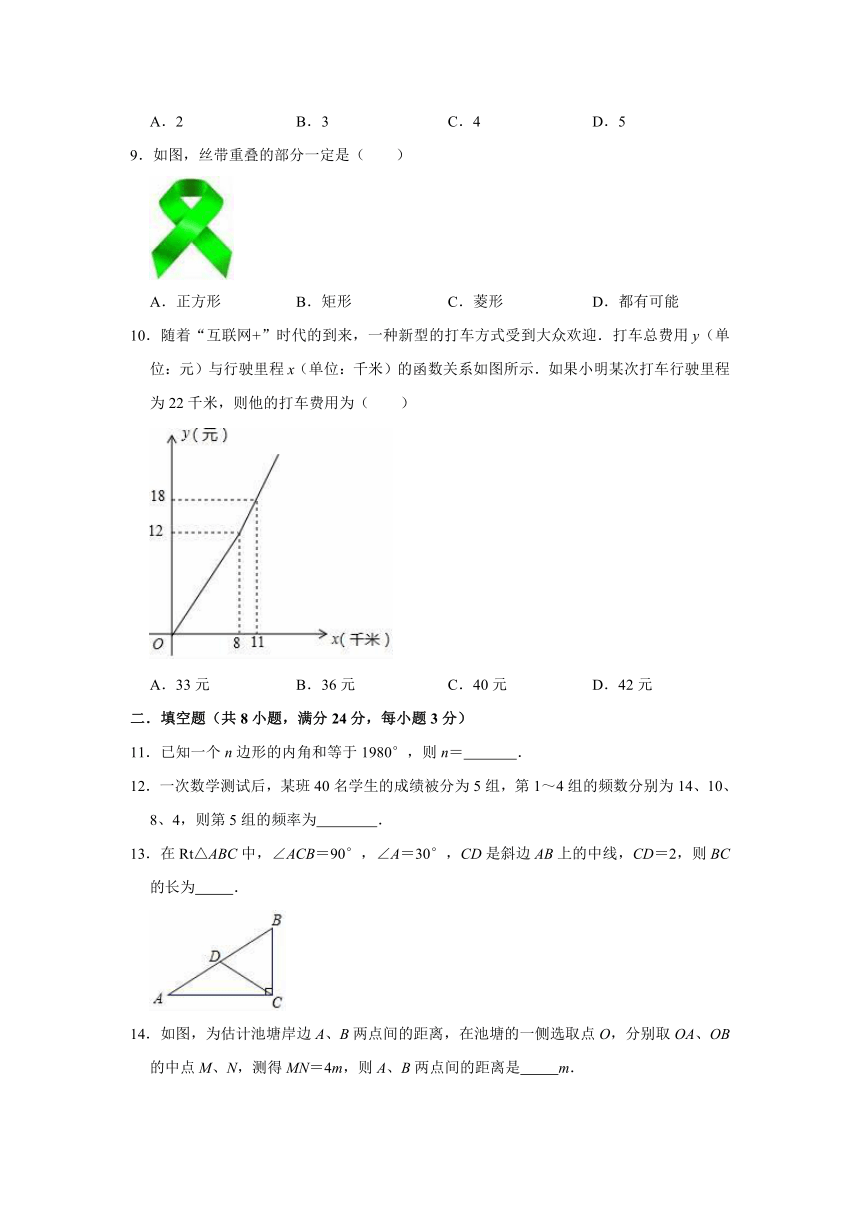
9.如图,丝带重叠的部分一定是( )
A.正方形
B.矩形
C.菱形
D.都有可能
10.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元
B.36元
C.40元
D.42元
二.填空题(共8小题,满分24分,每小题3分)
11.已知一个n边形的内角和等于1980°,则n=
.
12.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为14、10、8、4,则第5组的频率为
.
13.在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,CD=2,则BC的长为
.
14.如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=4m,则A、B两点间的距离是
m.
15.某一次函数的图象经过点(﹣1,3),且函数y随x的增大而减小,请你写出一个符合条件的函数解析式
.
16.如图,围棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,1),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是
.
17.已知直线y=kx+4,该直线与两坐标轴围成的三角形面积为8,那么k的值是
.
18.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(5,0),(0,3),点P在BC边上运动,当△OAP是等腰三角形时,点P的坐标为
.
三.解答题(共8小题,满分66分)
19.如图,四边形ABCD中,AB∥CD,AC与BD相交于点O,AO=CO,求证:四边形ABCD是平行四边形.
20.如图,在四边形ABCD中,AD∥BC,E为AB的中点,DE⊥CE.
(1)求作一个三角形与△ADE关于点E成中心对称,并说明AD的对应边与四边形的边BC的位置关系.
(2)上述点D的对称点与点E,C构成的三角形与△DEC成轴对称吗?由此能得出关系AD+BC=DC吗?证明你的结论.
21.如图,学校有一块长方形花坛,有极少数人为了避开拐角走“捷径”,在花坛内走出了一条“路”,他们仅仅少走了
m,却踩伤了花草.
22.已知:y﹣2与x成正比例,且x=2时,y=4.
(1)求y关于x的函数表达式;
(2)若点M(m,3)在这个函数的图象上,求点M的坐标.
23.某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
各种图书
频数
频率
自然科学
400
0.20
文学艺术
1000
0.50
社会百科
m
0.25
哲学
n
(1)表中m=
,n=
;
(2)在图中,将表示“自然科学”的部分补充完整;
(3)若该学校打算采购一万册图书,请你估算“哲学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.
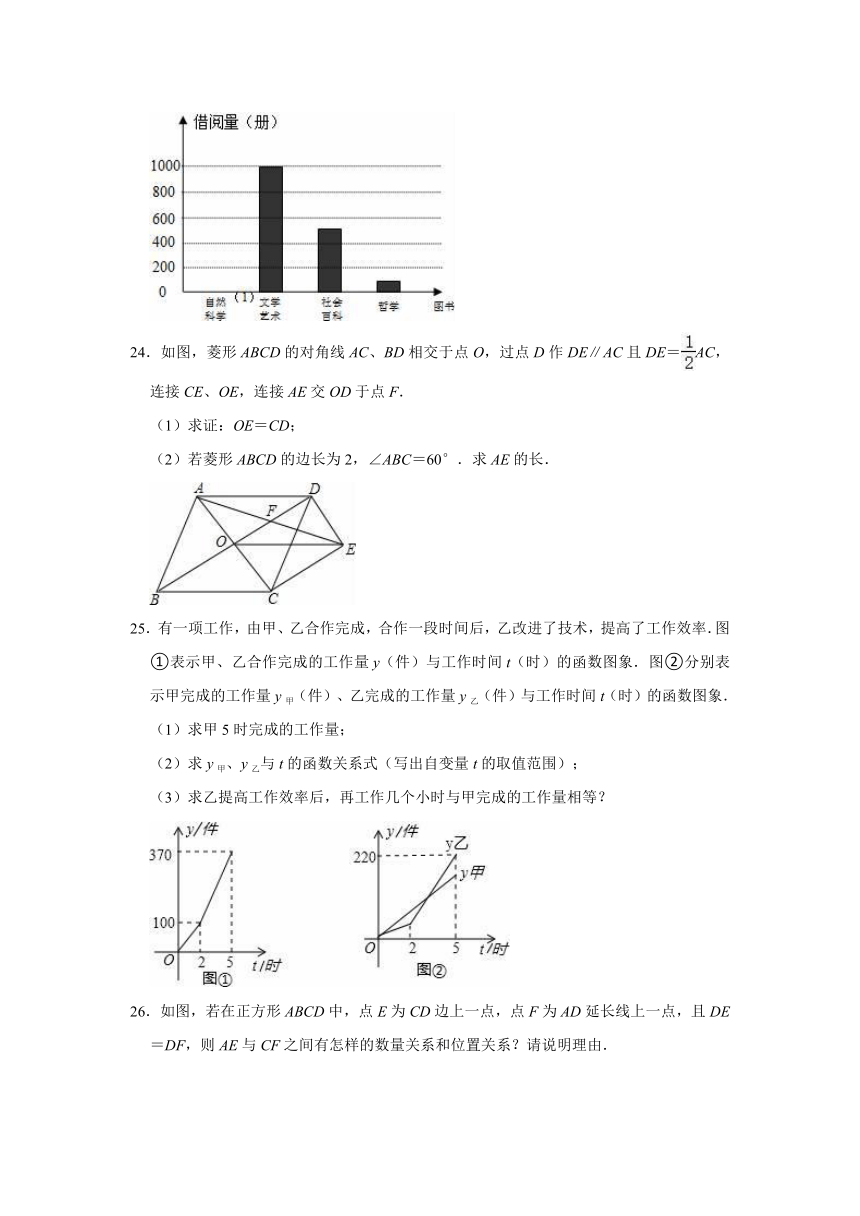
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°.求AE的长.
25.有一项工作,由甲、乙合作完成,合作一段时间后,乙改进了技术,提高了工作效率.图①表示甲、乙合作完成的工作量y(件)与工作时间t(时)的函数图象.图②分别表示甲完成的工作量y甲(件)、乙完成的工作量y乙(件)与工作时间t(时)的函数图象.
(1)求甲5时完成的工作量;
(2)求y甲、y乙与t的函数关系式(写出自变量t的取值范围);
(3)求乙提高工作效率后,再工作几个小时与甲完成的工作量相等?
26.如图,若在正方形ABCD中,点E为CD边上一点,点F为AD延长线上一点,且DE=DF,则AE与CF之间有怎样的数量关系和位置关系?请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、12+22≠32,不能构成直角三角形,故此选项不符合题意;
B、()2+()2≠()2,不能构成直角三角形,故此选项不符合题意;
C、42+52=()2,能构成直角三角形,故此选项符合题意;
D、62+82≠122,不能构成直角三角形,故此选项不符合题意.
故选:C.
2.解:从六边形的一个顶点出发,可引出的对角线共有:6﹣3=3(条),
故选:C.
3.解:A、是中心对称图形,也是轴对称图形,不符合题意;
B、不是中心对称图形,是轴对称图形,不符合题意;
C、是中心对称图形,不是轴对称图形,符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:C.
4.解:∵点P(a﹣3,a+2)在x轴上,
∴a+2=0,
∴a=﹣2.
故选:A.
5.解:∵直线y=kx+b经过第一、二、四象限,
∴k<0,b>0,
∴直线y=bx+k一定不经过第二象限.
故选:B.
6.解:①如图1,当点E在F右侧时,在?ABCD中,∵BC=AD=13,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=3,
∴BC=BE+CF﹣EF=2AB﹣EF=13,
∴AB=8;
②当点E在F左侧时,在?ABCD中,∵BC=AD=13,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=3,
∴BC=BE+CF=2AB+EF=13,
∴AB=5;
综上所述:AB的长为8或5.
故选:D.
7.解:由题意得,直线AB的解析式为y=2x+b,
∵直线AB恰好过点(6,2),
∴2=2×6+b,解得b=﹣10,
∴直线AB的表达式为y=2x﹣10,
故选:A.
8.解:①两条平行线被第三条直线所截,内错角相等,原命题是假命题.
②三角形的内角和是180°,是真命题.
③在同一平面内,平行于同一条直线的两条直线平行,是真命题.
④相等的角不一定是对顶角,原命题是假命题.
⑤两点之间,线段最短,是真命题;
故选:B.
9.解:过点A作AE⊥BC于E,AF⊥CD于F,因为两条彩带宽度相同,
所以AB∥CD,AD∥BC,AE=AF.
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AE=CD?AF.又AE=AF.
∴BC=CD,
∴四边形ABCD是菱形.
故选:C.
10.解:当行驶里程x≥8时,设y=kx+b,
将(8,12)、(11,18)代入,
得:,
解得:,
∴y=2x﹣4,
当x=22时,y=2×22﹣4=40,
∴如果小明某次打车行驶里程为22千米,则他的打车费用为40元;
故选:C.
二.填空题(共8小题,满分24分,每小题3分)
11.解:设这个多边形的边数为n,
则(n﹣2)?180°=1980°,
解得n=13.
故答案为:13.
12.解:第5组的频数:40﹣14﹣10﹣8﹣4=4,
第5组的频率:4÷40=0.1,
故答案为:0.1.
13.解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴AB=2CD=2×2=4,
∵∠ACB=90°,∠A=30°,
∴BC=AB=2,
故答案为:2.
14.解:∵M、N是OA、OB的中点,即MN是△OAB的中位线,
∴MN=AB,
∴AB=2MN=2×4=8(m).
故答案为:8.
15.解:该一次函数的解析式为y=kx+b(k<0),
∵一次函数的图象经过点(﹣1,3),
∴﹣k+b=3,
∴当k=﹣1时,b=2,
∴符合条件的函数关系式可以是:y=﹣x+2(答案不唯一).
16.解:如图:
白棋(甲)的坐标是(3,﹣1),
故答案为:(3,﹣1).
17.解:∵当x=0时,y=4,
当y=0时,x=﹣,
∴直线与y轴的交点分别为(0,4),与x轴的交点分别为(﹣,0),
∴×4×|﹣|=8,
解得,k=±1,
故答案为:k=±1.
18.解:∵四边形OABC是矩形,顶点A、C的坐标分别为(5,0)、(0,3),
∴∠B=90°,OC=AB=3,OA=BC=5,
作PM⊥OA于M,如图:
则PM=OC=3,
当△OAP是等腰三角形时,分三种情况:
①PO=PA时,点P在OA的垂直平分线上,OM=AM=OA=,
∴P点的坐标为:(,3);
②OP=OA=5时,OM===4,
∴P点的坐标为:(4,3);
③AP=OA=5时,AM==4,
∴OM=OA﹣AM=1,
∴P点的坐标为:(1,3);
综上所述,P点的坐标为:(,3)或(4,3)或(1,3);
故答案为:(,3)或(4,3)或(1,3).
三.解答题(共8小题,满分66分)
19.证明:∵AB∥CD,
∴∠DCO=∠BAO,
在△DCO和△BAO中,
,
∴△DCO≌△BAO(ASA),
∴DO=BO,
∵AO=CO,
∴四边形ABCD是平行四边形.
20.解:(1)如图所示,
∵AE=BE,
∴AD的对应边在BC的反向延长线上;
(2)成轴对称,AD+BC=DC.
∵△ADE与△A′D′E关于点E对称,
∴DE=D′E.
∵DE⊥CE,
∴点D的对称点与点E,C构成的三角形与△DEC成轴对称.
∴D′C=DC,
∵AD=A′D′,
∴AD+BC=DC.
21.解:由题意得,斜边长为:=5m,
故少走的路程=两直角边之和﹣斜边=3+4﹣5=2m.
故答案为:2.
22.解:(1)设y﹣2=kx,
把x=2,y=4代入求得k=1,
∴函数解析式是y=x+2;
(2)∵点M(m,3)在这个函数图象上,
∴3=m+2,
解得:m=1,
∴M(1,3).
23.解:(1)400÷0.20=2000,
m=2000×0.25=500,
n=1﹣0.20﹣0.5﹣0.25=0.05;
故答案为500,0.05;
(2)如图,
(3)10000×0.05=500(册),
即估算“哲学”类图书应采购500册较合适;
(4)鼓励学生多借阅哲学类的书.
24.(1)证明:在菱形ABCD中,OC=AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD=.
在Rt△ACE中,
AE=.
25.解:(1)由图①得,总工作量为370件,由图②可得出乙完成了220件,
故甲5时完成的工作量是150.
(2)设y甲的函数解析式为y=kt(k≠0),把点(5,150)代入可得:k=30
故y甲=30t(0≤t≤5);
乙改进前,甲乙每小时完成50件,所以乙每小时完成20件,
当0≤t≤2时,可得y乙=20t;
当2<t≤5时,设y=ct+d,将点(2,40),(5,220)代入可得:,
解得:
故y乙=60t﹣80(2<t≤5).
综上可得:y甲=30t(0≤t≤5);y乙=.
(3)由题意得:,
解得:t=,
故改进后﹣2=小时后乙与甲完成的工作量相等.
26.解:AE=CF,AE⊥CF,理由如下:
如图,延长AE交CF于点G,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=∠CDE=90°,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴AE=CF,∠DAE=∠DCF,
∵∠DCF+∠F=90°,
∴∠DAE+∠F=90°,
∴AG⊥CF,
即AE⊥CF.
∴AE=CF,AE⊥CF.
一.选择题(共10小题,满分30分,每小题3分)
1.下列各组数中能作为直角三角形的三边长的是( )
A.1,2,3
B.,,
C.4,5,
D.6,8,12
2.从六边形的一个顶点出发,可引出的对角线共有( )
A.1条
B.2条
C.3条
D.4条
3.下列图案中是中心对称图形但不是轴对称图形的是( )
A.
B.
C.
D.
4.已知点P(a﹣3,a+2)在x轴上,则a=( )
A.﹣2
B.3
C.﹣5
D.5
5.已知直线y=kx+b经过第一、二、四象限,那么直线y=bx+k一定不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.在?ABCD中,AD=13,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=3,则AB的长( )
A.8
B.5
C.3或5
D.5或8
7.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB恰好过点(6,2),则直线AB的表达式为( )
A.y=2x﹣10
B.y=﹣2x+14
C.y=2x+2
D.y=﹣x+5
8.下列命题是真命题的个数为( )
①两条直线被第三条直线所截,内错角相等.
②三角形的内角和是180°.
③在同一平面内,平行于同一条直线的两条直线平行.
④相等的角是对顶角.
⑤两点之间,线段最短.
A.2
B.3
C.4
D.5
9.如图,丝带重叠的部分一定是( )
A.正方形
B.矩形
C.菱形
D.都有可能
10.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元
B.36元
C.40元
D.42元
二.填空题(共8小题,满分24分,每小题3分)
11.已知一个n边形的内角和等于1980°,则n=
.
12.一次数学测试后,某班40名学生的成绩被分为5组,第1~4组的频数分别为14、10、8、4,则第5组的频率为
.
13.在Rt△ABC中,∠ACB=90°,∠A=30°,CD是斜边AB上的中线,CD=2,则BC的长为
.
14.如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=4m,则A、B两点间的距离是
m.
15.某一次函数的图象经过点(﹣1,3),且函数y随x的增大而减小,请你写出一个符合条件的函数解析式
.
16.如图,围棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为(﹣2,1),黑棋(乙)的坐标为(﹣1,﹣2),则白棋(甲)的坐标是
.
17.已知直线y=kx+4,该直线与两坐标轴围成的三角形面积为8,那么k的值是
.
18.如图,在平面直角坐标系中,矩形OABC的顶点A,C的坐标分别为(5,0),(0,3),点P在BC边上运动,当△OAP是等腰三角形时,点P的坐标为
.
三.解答题(共8小题,满分66分)
19.如图,四边形ABCD中,AB∥CD,AC与BD相交于点O,AO=CO,求证:四边形ABCD是平行四边形.
20.如图,在四边形ABCD中,AD∥BC,E为AB的中点,DE⊥CE.
(1)求作一个三角形与△ADE关于点E成中心对称,并说明AD的对应边与四边形的边BC的位置关系.
(2)上述点D的对称点与点E,C构成的三角形与△DEC成轴对称吗?由此能得出关系AD+BC=DC吗?证明你的结论.
21.如图,学校有一块长方形花坛,有极少数人为了避开拐角走“捷径”,在花坛内走出了一条“路”,他们仅仅少走了
m,却踩伤了花草.
22.已知:y﹣2与x成正比例,且x=2时,y=4.
(1)求y关于x的函数表达式;
(2)若点M(m,3)在这个函数的图象上,求点M的坐标.
23.某中学图书馆将图书分为自然科学、文学艺术、社会百科、哲学四类.在“读书月”活动中,为了了解图书的借阅情况,图书管理员对本月各类图书的借阅进行了统计,表)和图是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图.请你根据图表中提供的信息,解答以下问题:
各种图书
频数
频率
自然科学
400
0.20
文学艺术
1000
0.50
社会百科
m
0.25
哲学
n
(1)表中m=
,n=
;
(2)在图中,将表示“自然科学”的部分补充完整;
(3)若该学校打算采购一万册图书,请你估算“哲学”类图书应采购多少册较合适?
(4)根据图表提供的信息,请你提出一条合理化的建议.
24.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接CE、OE,连接AE交OD于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°.求AE的长.
25.有一项工作,由甲、乙合作完成,合作一段时间后,乙改进了技术,提高了工作效率.图①表示甲、乙合作完成的工作量y(件)与工作时间t(时)的函数图象.图②分别表示甲完成的工作量y甲(件)、乙完成的工作量y乙(件)与工作时间t(时)的函数图象.
(1)求甲5时完成的工作量;
(2)求y甲、y乙与t的函数关系式(写出自变量t的取值范围);
(3)求乙提高工作效率后,再工作几个小时与甲完成的工作量相等?
26.如图,若在正方形ABCD中,点E为CD边上一点,点F为AD延长线上一点,且DE=DF,则AE与CF之间有怎样的数量关系和位置关系?请说明理由.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、12+22≠32,不能构成直角三角形,故此选项不符合题意;
B、()2+()2≠()2,不能构成直角三角形,故此选项不符合题意;
C、42+52=()2,能构成直角三角形,故此选项符合题意;
D、62+82≠122,不能构成直角三角形,故此选项不符合题意.
故选:C.
2.解:从六边形的一个顶点出发,可引出的对角线共有:6﹣3=3(条),
故选:C.
3.解:A、是中心对称图形,也是轴对称图形,不符合题意;
B、不是中心对称图形,是轴对称图形,不符合题意;
C、是中心对称图形,不是轴对称图形,符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:C.
4.解:∵点P(a﹣3,a+2)在x轴上,
∴a+2=0,
∴a=﹣2.
故选:A.
5.解:∵直线y=kx+b经过第一、二、四象限,
∴k<0,b>0,
∴直线y=bx+k一定不经过第二象限.
故选:B.
6.解:①如图1,当点E在F右侧时,在?ABCD中,∵BC=AD=13,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=3,
∴BC=BE+CF﹣EF=2AB﹣EF=13,
∴AB=8;
②当点E在F左侧时,在?ABCD中,∵BC=AD=13,BC∥AD,CD=AB,CD∥AB,
∴∠DAE=∠AEB,∠ADF=∠DFC,
∵AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,
∴∠BAE=∠DAE,∠ADF=∠CDF,
∴∠BAE=∠AEB,∠CFD=∠CDF,
∴AB=BE,CF=CD,
∵EF=3,
∴BC=BE+CF=2AB+EF=13,
∴AB=5;
综上所述:AB的长为8或5.
故选:D.
7.解:由题意得,直线AB的解析式为y=2x+b,
∵直线AB恰好过点(6,2),
∴2=2×6+b,解得b=﹣10,
∴直线AB的表达式为y=2x﹣10,
故选:A.
8.解:①两条平行线被第三条直线所截,内错角相等,原命题是假命题.
②三角形的内角和是180°,是真命题.
③在同一平面内,平行于同一条直线的两条直线平行,是真命题.
④相等的角不一定是对顶角,原命题是假命题.
⑤两点之间,线段最短,是真命题;
故选:B.
9.解:过点A作AE⊥BC于E,AF⊥CD于F,因为两条彩带宽度相同,
所以AB∥CD,AD∥BC,AE=AF.
∴四边形ABCD是平行四边形.
∵S?ABCD=BC?AE=CD?AF.又AE=AF.
∴BC=CD,
∴四边形ABCD是菱形.
故选:C.
10.解:当行驶里程x≥8时,设y=kx+b,
将(8,12)、(11,18)代入,
得:,
解得:,
∴y=2x﹣4,
当x=22时,y=2×22﹣4=40,
∴如果小明某次打车行驶里程为22千米,则他的打车费用为40元;
故选:C.
二.填空题(共8小题,满分24分,每小题3分)
11.解:设这个多边形的边数为n,
则(n﹣2)?180°=1980°,
解得n=13.
故答案为:13.
12.解:第5组的频数:40﹣14﹣10﹣8﹣4=4,
第5组的频率:4÷40=0.1,
故答案为:0.1.
13.解:在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴AB=2CD=2×2=4,
∵∠ACB=90°,∠A=30°,
∴BC=AB=2,
故答案为:2.
14.解:∵M、N是OA、OB的中点,即MN是△OAB的中位线,
∴MN=AB,
∴AB=2MN=2×4=8(m).
故答案为:8.
15.解:该一次函数的解析式为y=kx+b(k<0),
∵一次函数的图象经过点(﹣1,3),
∴﹣k+b=3,
∴当k=﹣1时,b=2,
∴符合条件的函数关系式可以是:y=﹣x+2(答案不唯一).
16.解:如图:
白棋(甲)的坐标是(3,﹣1),
故答案为:(3,﹣1).
17.解:∵当x=0时,y=4,
当y=0时,x=﹣,
∴直线与y轴的交点分别为(0,4),与x轴的交点分别为(﹣,0),
∴×4×|﹣|=8,
解得,k=±1,
故答案为:k=±1.
18.解:∵四边形OABC是矩形,顶点A、C的坐标分别为(5,0)、(0,3),
∴∠B=90°,OC=AB=3,OA=BC=5,
作PM⊥OA于M,如图:
则PM=OC=3,
当△OAP是等腰三角形时,分三种情况:
①PO=PA时,点P在OA的垂直平分线上,OM=AM=OA=,
∴P点的坐标为:(,3);
②OP=OA=5时,OM===4,
∴P点的坐标为:(4,3);
③AP=OA=5时,AM==4,
∴OM=OA﹣AM=1,
∴P点的坐标为:(1,3);
综上所述,P点的坐标为:(,3)或(4,3)或(1,3);
故答案为:(,3)或(4,3)或(1,3).
三.解答题(共8小题,满分66分)
19.证明:∵AB∥CD,
∴∠DCO=∠BAO,
在△DCO和△BAO中,
,
∴△DCO≌△BAO(ASA),
∴DO=BO,
∵AO=CO,
∴四边形ABCD是平行四边形.
20.解:(1)如图所示,
∵AE=BE,
∴AD的对应边在BC的反向延长线上;
(2)成轴对称,AD+BC=DC.
∵△ADE与△A′D′E关于点E对称,
∴DE=D′E.
∵DE⊥CE,
∴点D的对称点与点E,C构成的三角形与△DEC成轴对称.
∴D′C=DC,
∵AD=A′D′,
∴AD+BC=DC.
21.解:由题意得,斜边长为:=5m,
故少走的路程=两直角边之和﹣斜边=3+4﹣5=2m.
故答案为:2.
22.解:(1)设y﹣2=kx,
把x=2,y=4代入求得k=1,
∴函数解析式是y=x+2;
(2)∵点M(m,3)在这个函数图象上,
∴3=m+2,
解得:m=1,
∴M(1,3).
23.解:(1)400÷0.20=2000,
m=2000×0.25=500,
n=1﹣0.20﹣0.5﹣0.25=0.05;
故答案为500,0.05;
(2)如图,
(3)10000×0.05=500(册),
即估算“哲学”类图书应采购500册较合适;
(4)鼓励学生多借阅哲学类的书.
24.(1)证明:在菱形ABCD中,OC=AC.
∴DE=OC.
∵DE∥AC,
∴四边形OCED是平行四边形.
∵AC⊥BD,
∴平行四边形OCED是矩形.
∴OE=CD.
(2)在菱形ABCD中,∠ABC=60°,
∴AC=AB=2.
∴在矩形OCED中,
CE=OD=.
在Rt△ACE中,
AE=.
25.解:(1)由图①得,总工作量为370件,由图②可得出乙完成了220件,
故甲5时完成的工作量是150.
(2)设y甲的函数解析式为y=kt(k≠0),把点(5,150)代入可得:k=30
故y甲=30t(0≤t≤5);
乙改进前,甲乙每小时完成50件,所以乙每小时完成20件,
当0≤t≤2时,可得y乙=20t;
当2<t≤5时,设y=ct+d,将点(2,40),(5,220)代入可得:,
解得:
故y乙=60t﹣80(2<t≤5).
综上可得:y甲=30t(0≤t≤5);y乙=.
(3)由题意得:,
解得:t=,
故改进后﹣2=小时后乙与甲完成的工作量相等.
26.解:AE=CF,AE⊥CF,理由如下:
如图,延长AE交CF于点G,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=∠CDE=90°,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴AE=CF,∠DAE=∠DCF,
∵∠DCF+∠F=90°,
∴∠DAE+∠F=90°,
∴AG⊥CF,
即AE⊥CF.
∴AE=CF,AE⊥CF.
同课章节目录
