2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 212.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 08:23:44 | ||
图片预览


文档简介
2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题
一.选择题(共12小题,满分36分,每小题3分)
1.在新冠肺炎防控期间,要了解某学校以下情况,其中适合用普查的有( )
①了解学校口罩、洗手液、消毒片的储备情况;
②了解全体师生在寒假期间的离校情况;
③了解全体师生入校时的体温情况;
④了解全体师生对“七步洗手法”的运用情况.
A.1个
B.2个
C.3个
D.4个
2.永定河,“北京的母亲河”.近年来,我区政府在永定河治理过程中,有时会将弯曲的河道改直,图中A、B两地间的河道改直后大大缩短了河道的长度.这一做法的主要依据是( )
A.两点确定一条直线
B.垂线段最短
C.过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
3.(1﹣2x)(1+2x)的计算结果是( )
A.4x2+1
B.1﹣4x2
C.4x2
D.﹣4x2﹣1
4.如图,能判断直线AB∥CD的条件是( )
A.∠1=∠2
B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180°
5.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等
B.互余或互补
C.互补
D.相等或互补
6.2020年1月24日,中国疾控中心成功分离我国首株新型冠状病毒毒种,该毒种直径大约为80纳米(1纳米=0.000001毫米),数据“80纳米”用科学记数法表示为( )
A.0.8×10﹣7毫米
B.8×10﹣6毫米
C.8×10﹣5毫米
D.80×10﹣6毫米
7.下列运算不正确的是( )
A.a2?a3=a5
B.(y3)4=y12
C.(﹣2x)3=﹣8x3
D.x3+x3=2x6
8.温州6月8日~14日的气温折线统计图如图所示,其中实线表示当日最高气温,虚线表示当日最低气温,由图可知,这一周中温差最大的是( )
A.6月9日
B.6月11日
C.6月12日
D.6月14日
9.如图,点D是线段AB的中点,点C是线段AD的中点.若AB=16cm,则线段BC=( )
A.4cm
B.10cm
C.12cm
D.14cm
10.如表为一个图案中红色和白色瓷砖数量的关系.设r和w分别为红色和白色瓷砖的数量,下列函数表达式可以表示w与r之间的关系的是( )
红色瓷砖数量(r)
3
4
5
6
7
白色瓷砖数量(w)
6
8
10
12
14
A.w=r+3
B.w=2r
C.w=
D.w=r+7
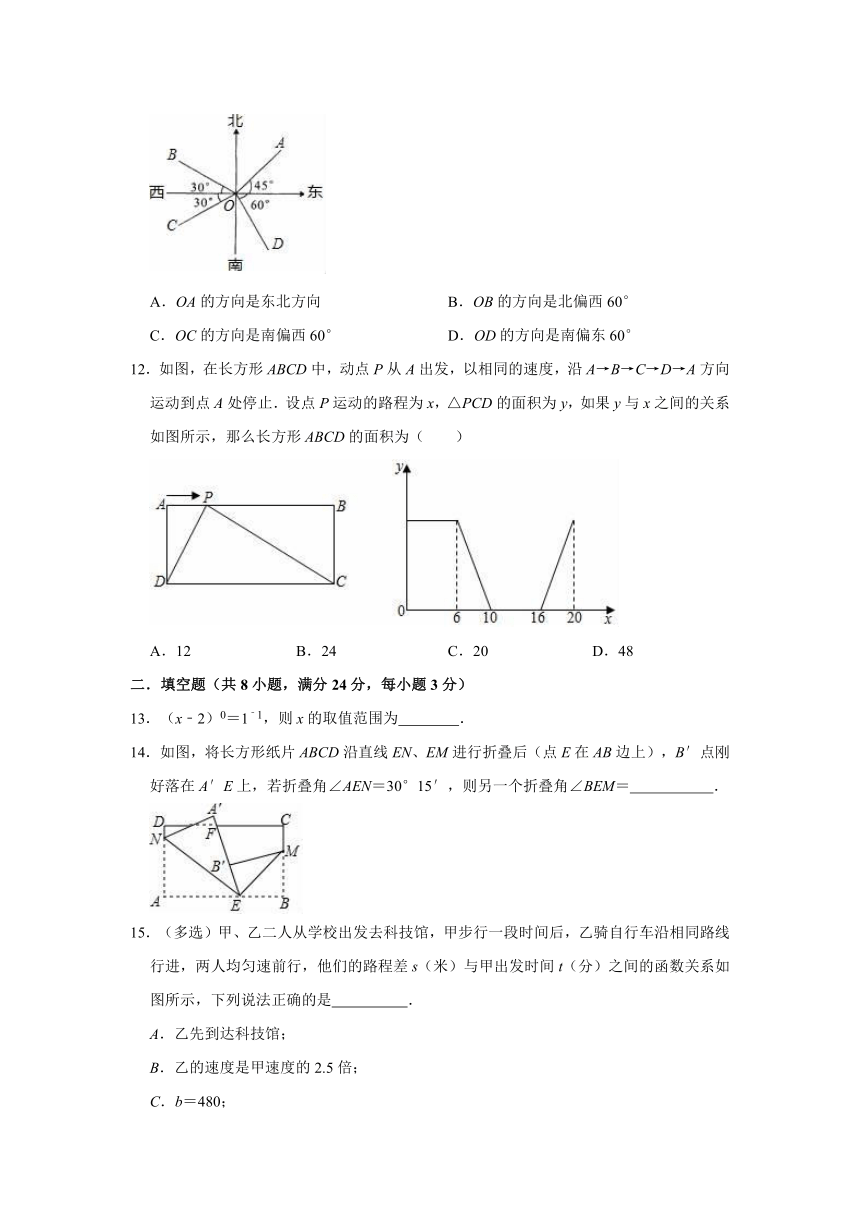
11.如图,下列说法中错误的是( )
A.OA的方向是东北方向
B.OB的方向是北偏西60°
C.OC的方向是南偏西60°
D.OD的方向是南偏东60°
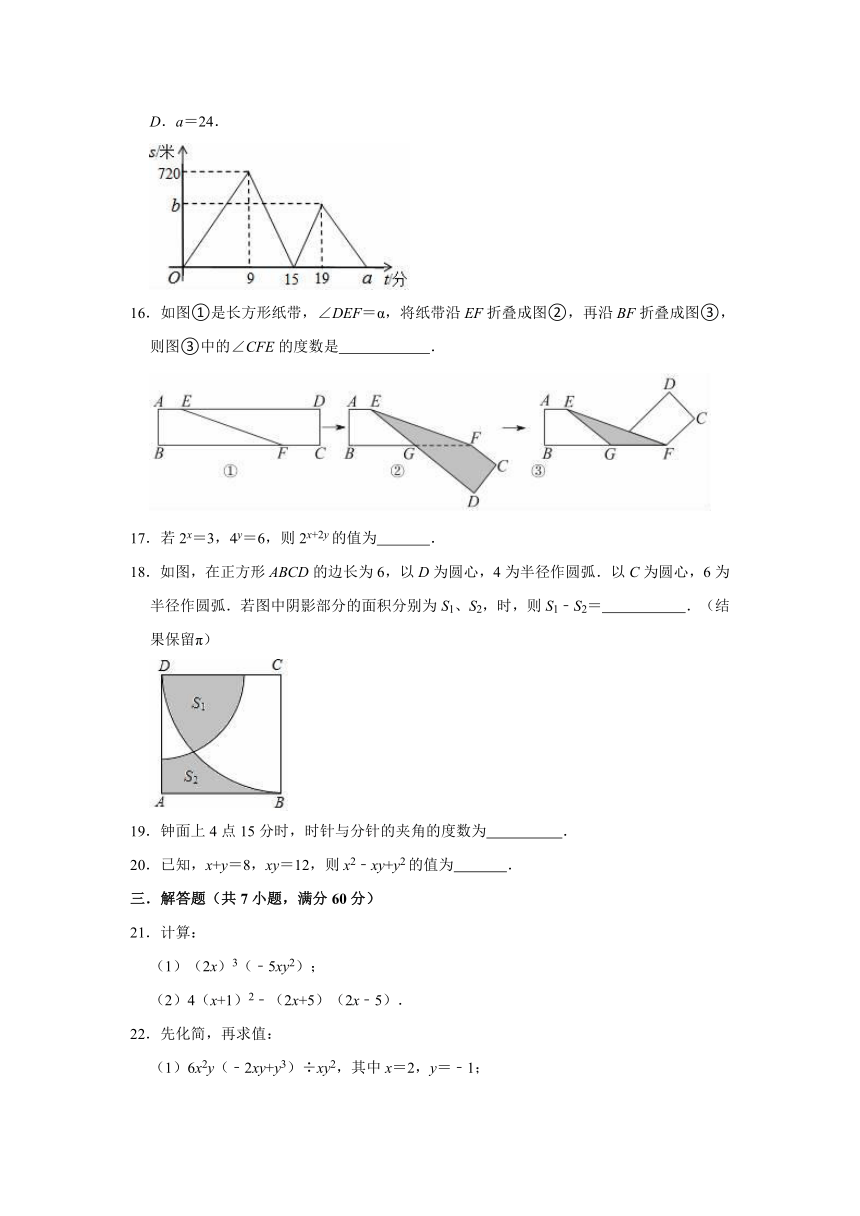
12.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.12
B.24
C.20
D.48
二.填空题(共8小题,满分24分,每小题3分)
13.(x﹣2)0=1﹣1,则x的取值范围为
.
14.如图,将长方形纸片ABCD沿直线EN、EM进行折叠后(点E在AB边上),B′点刚好落在A′E上,若折叠角∠AEN=30°15′,则另一个折叠角∠BEM=
.
15.(多选)甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示,下列说法正确的是
.
A.乙先到达科技馆;
B.乙的速度是甲速度的2.5倍;
C.b=480;
D.a=24.
16.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是
.
17.若2x=3,4y=6,则2x+2y的值为
.
18.如图,在正方形ABCD的边长为6,以D为圆心,4为半径作圆弧.以C为圆心,6为半径作圆弧.若图中阴影部分的面积分别为S1、S2,时,则S1﹣S2=
.(结果保留π)
19.钟面上4点15分时,时针与分针的夹角的度数为
.
20.已知,x+y=8,xy=12,则x2﹣xy+y2的值为
.
三.解答题(共7小题,满分60分)
21.计算:
(1)(2x)3(﹣5xy2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
22.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
23.如图,直线AB、CD相交于点O,∠AOC=50°,∠1=20°.求:∠AOD和∠2的度数.
24.2020年,周至县小李家的猕猴桃喜获丰收.在销售过程中,猕猴桃的销售额y(元)与销量x(千克)满足如下关系:
销售量x(千克)
1
2
3
4
5
6
7
8
销售额y(元)
6
12
18
24
30
36
42
48
(1)在这个变化过程中,自变量是
,因变量是
;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为
;
(3)当猕猴桃销售量为100千克时,销售额是多少元?
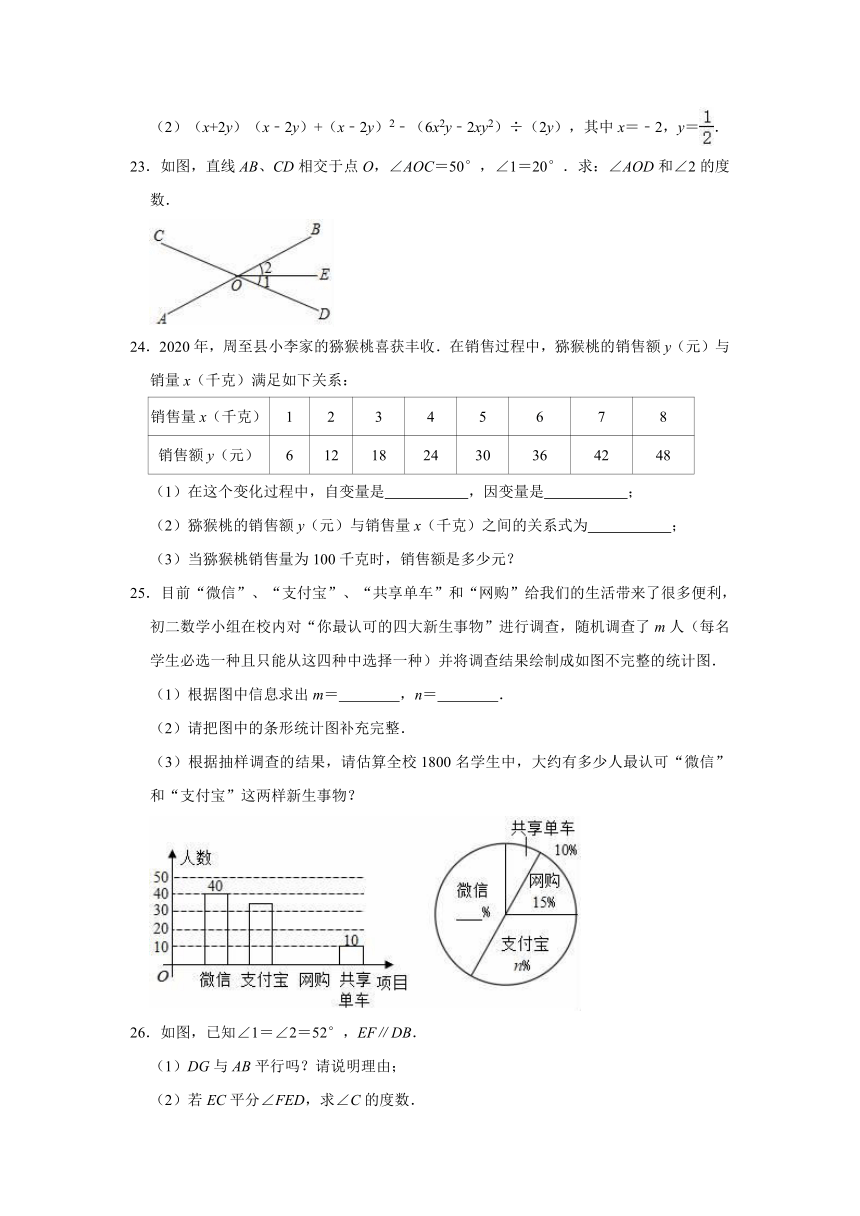
25.目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如图不完整的统计图.
(1)根据图中信息求出m=
,n=
.
(2)请把图中的条形统计图补充完整.
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人最认可“微信”和“支付宝”这两样新生事物?
26.如图,已知∠1=∠2=52°,EF∥DB.
(1)DG与AB平行吗?请说明理由;
(2)若EC平分∠FED,求∠C的度数.
27.小明从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,小明的家、体育场、文具店在同一条直线上.如图是小明离家的距离与时间的关系图象.根据图象回答下列问题:
(1)体育场离小明家
千米.
(2)小明在文具店逗留了
分钟.
(3)求小明从文具店到家的速度是
千米/时.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:①了解学校口罩、洗手液、消毒片的储备情况适合普查;
②了解全体师生在寒假期间的离锡情况适合普查;
③了解全体师生入校时的体温情况适合普查;
④了解全体师生对“七步洗手法”的运用情况适合抽样调查.
故选:C.
2.解:把原来弯曲的河道改直,A、B两地间的河道长度就发生了变化,
这一做法的主要依据是:两点之间线段最短.
故选:D.
3.解:(1﹣2x)(1+2x)
=12﹣(2x)2
=1﹣4x2,
故选:B.
4.解:∵∠3+∠5=180°,
而当∠4=∠5时,AB∥CD,
当∠3+∠4=180°,
而∠3+∠5=180°,
所以∠4=∠5,则AB∥CD.
故选:D.
5.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
6.解:∵1纳米=0.000001毫米,
∴80纳米=0.00008毫米=8×10﹣5毫米.
故选:C.
7.解:A.a2?a3=a2+3=a5,故本选项不合题意;
B.(y3)4=y3×4=y12,故本选项不合题意;
C.(﹣2x)3=(﹣2)3x3=﹣8x3,故本选项不合题意;
D.x3+x3=2x3,故本选项符合题意.
故选:D.
8.解:由图形直观可以得出6月14日温差最大,是35﹣25=10(℃),
故选:D.
9.解:∵点D是线段AB的中点,
∴AD=BD=AB=×16=8(cm),
∵C是线段AD的中点,
∴CD=AD=×8=4(cm).
∴BC=CD+BD=4+8=12(cm).
故选:C.
10.解:根据表格可知,w与r之间的关系是w=2r,
故选:B.
11.解:A、OA的方向是北偏东45度即东北方向,故正确;
B、OB的方向是北偏西60°,故正确;
C、OC的方向是南偏西60°,故正确;
D、OD的方向是南偏东30°,故错误.
故选:D.
12.解:由题意可知,当点P从点A运动到点B时,△PCD的面积不变,结合图象可知AB=6,
当点P从点B运动到点C时,△PCD的面积逐渐变小直到为0,结合图象可知BC=4,
∴长方形ABCD的面积为:AB?BC=6×4=24.
故选:B.
二.填空题(共8小题,满分24分,每小题3分)
13.解:∵(x﹣2)0=1﹣1=1,
∴x﹣2≠0,
∴x的取值范围为:x≠2.
故答案为:x≠2.
14.解:由折叠性质得:∠AEN=∠A′EN,∠BEM=∠B′EM,
∴∠A′EN=30°15′,
∠BEM=(180°﹣∠AEN﹣∠A′EN)=(180°﹣30°15′﹣30°15′)=59°45′,
故答案为:59°45′.
15.解:由图象得出甲步行720米,需要9分钟,所以甲的运动速度为:720÷9=80(m/分),
当第15分钟时,乙运动15﹣9=6(分钟),
运动距离为:15×80=1200(m),
∴乙的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,故B正确;
当第19分钟以后两人之间距离越来越近,说明乙已经到达终点,则乙先到达科技馆,故A正确;
此时乙运动19﹣9=10(分钟),
运动总距离为:10×200=2000(m),
∴甲运动时间为:2000÷80=25(分钟),
故a的值为25,故D错误;
∵甲19分钟运动距离为:19×80=1520(m),
∴b=2000﹣1520=480,故C正确.
故答案为:A、B、C.
16.解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
故答案为:180°﹣3α.
17.解:因为2x=3,4y=6,
所以2x+2y=2x?22y=2x?4y=3×6=18,
故答案为:18.
18.解:由图可知,
S1+S3=π×42×=4π,
S2+S3=6×6﹣π×62×=36﹣9π,
∴(S1+S3)﹣(S2+S3)=4π﹣(36﹣9π)
即S1﹣S2=13π﹣36,
故答案为:13π﹣36.
19.解:时针与分针的夹角的度数=4×30°+15×0.5°﹣15×6°=37.5°.
故答案为37.5°.
20.解:∵x+y=8,xy=12,
∴原式=(x+y)2﹣3xy=82﹣3×12=64﹣36=28.
故答案为28.
三.解答题(共7小题,满分60分)
21.解:(1)(2x)3(﹣5xy2)
=8x3?(﹣5xy2)
=﹣40x4y2;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
22.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
23.解:∠AOD=180°﹣∠AOC=180°﹣50°=130°.
∠BOD=∠AOC=50°,
∠2=∠BOD﹣∠1=50°﹣20°=30°.
答:∠AOD和∠2的度数分别为130°和30°.
24.解:(1)在这个变化过程中,自变量是猕猴桃的销量,因变量是猕猴桃的销售额,
故答案为:猕猴桃的销量,猕猴桃的销售额;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为y=6x,
故答案为:y=6x;
(3)将x=100代入y=6x,可得y=6×100=600,
答:当猕猴桃销售量为100千克时,销售额是600元.
25.解:(1)10÷10%=100(人),即m=100,
“网购”人数;100×15%=15(人),
“支付宝”人数:100﹣40﹣15﹣10=35(人),35÷100=35%,因此n=35,
故答案为:100,35;
(2)补全条形统计图如图所示:
(3)1800×=1350(人),
答:全校1800名学生中,最认可“微信”和“支付宝”这两样新生事物的大约有1350人.
26.解:(1)DG与AB平行.理由:
∵EF∥DB,
∴∠1=∠D.
∵∠1=∠2,
∴∠D=∠2.
∴DG∥AB.
(2)∵EC平分∠FED,
∴∠DEC=∠DEF.
∵∠1=52°,
∴∠DEF=180°﹣∠1=128°.
∴∠DEC=∠DEF=64°.
∵DG∥AB,
∴∠C=∠DEC=64°.
27.解:(1)由图象可知,体育场离小明家2.5千米.
故答案为:2.5;
(2)由图象可知,小明在文具店逗留了:65﹣45=20(分钟).
故答案为:20;
(3)1.5÷=(km/h),
即小明从文具店到家的速度为km/h.
故答案为:.
一.选择题(共12小题,满分36分,每小题3分)
1.在新冠肺炎防控期间,要了解某学校以下情况,其中适合用普查的有( )
①了解学校口罩、洗手液、消毒片的储备情况;
②了解全体师生在寒假期间的离校情况;
③了解全体师生入校时的体温情况;
④了解全体师生对“七步洗手法”的运用情况.
A.1个
B.2个
C.3个
D.4个
2.永定河,“北京的母亲河”.近年来,我区政府在永定河治理过程中,有时会将弯曲的河道改直,图中A、B两地间的河道改直后大大缩短了河道的长度.这一做法的主要依据是( )
A.两点确定一条直线
B.垂线段最短
C.过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
3.(1﹣2x)(1+2x)的计算结果是( )
A.4x2+1
B.1﹣4x2
C.4x2
D.﹣4x2﹣1
4.如图,能判断直线AB∥CD的条件是( )
A.∠1=∠2
B.∠3=∠4
C.∠1+∠3=180°
D.∠3+∠4=180°
5.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等
B.互余或互补
C.互补
D.相等或互补
6.2020年1月24日,中国疾控中心成功分离我国首株新型冠状病毒毒种,该毒种直径大约为80纳米(1纳米=0.000001毫米),数据“80纳米”用科学记数法表示为( )
A.0.8×10﹣7毫米
B.8×10﹣6毫米
C.8×10﹣5毫米
D.80×10﹣6毫米
7.下列运算不正确的是( )
A.a2?a3=a5
B.(y3)4=y12
C.(﹣2x)3=﹣8x3
D.x3+x3=2x6
8.温州6月8日~14日的气温折线统计图如图所示,其中实线表示当日最高气温,虚线表示当日最低气温,由图可知,这一周中温差最大的是( )
A.6月9日
B.6月11日
C.6月12日
D.6月14日
9.如图,点D是线段AB的中点,点C是线段AD的中点.若AB=16cm,则线段BC=( )
A.4cm
B.10cm
C.12cm
D.14cm
10.如表为一个图案中红色和白色瓷砖数量的关系.设r和w分别为红色和白色瓷砖的数量,下列函数表达式可以表示w与r之间的关系的是( )
红色瓷砖数量(r)
3
4
5
6
7
白色瓷砖数量(w)
6
8
10
12
14
A.w=r+3
B.w=2r
C.w=
D.w=r+7
11.如图,下列说法中错误的是( )
A.OA的方向是东北方向
B.OB的方向是北偏西60°
C.OC的方向是南偏西60°
D.OD的方向是南偏东60°
12.如图,在长方形ABCD中,动点P从A出发,以相同的速度,沿A→B→C→D→A方向运动到点A处停止.设点P运动的路程为x,△PCD的面积为y,如果y与x之间的关系如图所示,那么长方形ABCD的面积为( )
A.12
B.24
C.20
D.48
二.填空题(共8小题,满分24分,每小题3分)
13.(x﹣2)0=1﹣1,则x的取值范围为
.
14.如图,将长方形纸片ABCD沿直线EN、EM进行折叠后(点E在AB边上),B′点刚好落在A′E上,若折叠角∠AEN=30°15′,则另一个折叠角∠BEM=
.
15.(多选)甲、乙二人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的路程差s(米)与甲出发时间t(分)之间的函数关系如图所示,下列说法正确的是
.
A.乙先到达科技馆;
B.乙的速度是甲速度的2.5倍;
C.b=480;
D.a=24.
16.如图①是长方形纸带,∠DEF=α,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中的∠CFE的度数是
.
17.若2x=3,4y=6,则2x+2y的值为
.
18.如图,在正方形ABCD的边长为6,以D为圆心,4为半径作圆弧.以C为圆心,6为半径作圆弧.若图中阴影部分的面积分别为S1、S2,时,则S1﹣S2=
.(结果保留π)
19.钟面上4点15分时,时针与分针的夹角的度数为
.
20.已知,x+y=8,xy=12,则x2﹣xy+y2的值为
.
三.解答题(共7小题,满分60分)
21.计算:
(1)(2x)3(﹣5xy2);
(2)4(x+1)2﹣(2x+5)(2x﹣5).
22.先化简,再求值:
(1)6x2y(﹣2xy+y3)÷xy2,其中x=2,y=﹣1;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y),其中x=﹣2,y=.
23.如图,直线AB、CD相交于点O,∠AOC=50°,∠1=20°.求:∠AOD和∠2的度数.
24.2020年,周至县小李家的猕猴桃喜获丰收.在销售过程中,猕猴桃的销售额y(元)与销量x(千克)满足如下关系:
销售量x(千克)
1
2
3
4
5
6
7
8
销售额y(元)
6
12
18
24
30
36
42
48
(1)在这个变化过程中,自变量是
,因变量是
;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为
;
(3)当猕猴桃销售量为100千克时,销售额是多少元?
25.目前“微信”、“支付宝”、“共享单车”和“网购”给我们的生活带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行调查,随机调查了m人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如图不完整的统计图.
(1)根据图中信息求出m=
,n=
.
(2)请把图中的条形统计图补充完整.
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人最认可“微信”和“支付宝”这两样新生事物?
26.如图,已知∠1=∠2=52°,EF∥DB.
(1)DG与AB平行吗?请说明理由;
(2)若EC平分∠FED,求∠C的度数.
27.小明从家里跑步去体育场,在那里锻炼了一会儿后,又走到文具店去买笔,然后走回家,小明的家、体育场、文具店在同一条直线上.如图是小明离家的距离与时间的关系图象.根据图象回答下列问题:
(1)体育场离小明家
千米.
(2)小明在文具店逗留了
分钟.
(3)求小明从文具店到家的速度是
千米/时.
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:①了解学校口罩、洗手液、消毒片的储备情况适合普查;
②了解全体师生在寒假期间的离锡情况适合普查;
③了解全体师生入校时的体温情况适合普查;
④了解全体师生对“七步洗手法”的运用情况适合抽样调查.
故选:C.
2.解:把原来弯曲的河道改直,A、B两地间的河道长度就发生了变化,
这一做法的主要依据是:两点之间线段最短.
故选:D.
3.解:(1﹣2x)(1+2x)
=12﹣(2x)2
=1﹣4x2,
故选:B.
4.解:∵∠3+∠5=180°,
而当∠4=∠5时,AB∥CD,
当∠3+∠4=180°,
而∠3+∠5=180°,
所以∠4=∠5,则AB∥CD.
故选:D.
5.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
6.解:∵1纳米=0.000001毫米,
∴80纳米=0.00008毫米=8×10﹣5毫米.
故选:C.
7.解:A.a2?a3=a2+3=a5,故本选项不合题意;
B.(y3)4=y3×4=y12,故本选项不合题意;
C.(﹣2x)3=(﹣2)3x3=﹣8x3,故本选项不合题意;
D.x3+x3=2x3,故本选项符合题意.
故选:D.
8.解:由图形直观可以得出6月14日温差最大,是35﹣25=10(℃),
故选:D.
9.解:∵点D是线段AB的中点,
∴AD=BD=AB=×16=8(cm),
∵C是线段AD的中点,
∴CD=AD=×8=4(cm).
∴BC=CD+BD=4+8=12(cm).
故选:C.
10.解:根据表格可知,w与r之间的关系是w=2r,
故选:B.
11.解:A、OA的方向是北偏东45度即东北方向,故正确;
B、OB的方向是北偏西60°,故正确;
C、OC的方向是南偏西60°,故正确;
D、OD的方向是南偏东30°,故错误.
故选:D.
12.解:由题意可知,当点P从点A运动到点B时,△PCD的面积不变,结合图象可知AB=6,
当点P从点B运动到点C时,△PCD的面积逐渐变小直到为0,结合图象可知BC=4,
∴长方形ABCD的面积为:AB?BC=6×4=24.
故选:B.
二.填空题(共8小题,满分24分,每小题3分)
13.解:∵(x﹣2)0=1﹣1=1,
∴x﹣2≠0,
∴x的取值范围为:x≠2.
故答案为:x≠2.
14.解:由折叠性质得:∠AEN=∠A′EN,∠BEM=∠B′EM,
∴∠A′EN=30°15′,
∠BEM=(180°﹣∠AEN﹣∠A′EN)=(180°﹣30°15′﹣30°15′)=59°45′,
故答案为:59°45′.
15.解:由图象得出甲步行720米,需要9分钟,所以甲的运动速度为:720÷9=80(m/分),
当第15分钟时,乙运动15﹣9=6(分钟),
运动距离为:15×80=1200(m),
∴乙的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,故B正确;
当第19分钟以后两人之间距离越来越近,说明乙已经到达终点,则乙先到达科技馆,故A正确;
此时乙运动19﹣9=10(分钟),
运动总距离为:10×200=2000(m),
∴甲运动时间为:2000÷80=25(分钟),
故a的值为25,故D错误;
∵甲19分钟运动距离为:19×80=1520(m),
∴b=2000﹣1520=480,故C正确.
故答案为:A、B、C.
16.解:∵AD∥BC,
∴∠BFE=∠DEF=α,∠CFE=180°﹣∠DEF=180°﹣α,
∴∠CFG=∠CFE﹣∠BFE=180°﹣α﹣α=180°﹣2α,
∴∠CFE=∠CFG﹣∠BFE=180°﹣2α﹣α=180°﹣3α.
故答案为:180°﹣3α.
17.解:因为2x=3,4y=6,
所以2x+2y=2x?22y=2x?4y=3×6=18,
故答案为:18.
18.解:由图可知,
S1+S3=π×42×=4π,
S2+S3=6×6﹣π×62×=36﹣9π,
∴(S1+S3)﹣(S2+S3)=4π﹣(36﹣9π)
即S1﹣S2=13π﹣36,
故答案为:13π﹣36.
19.解:时针与分针的夹角的度数=4×30°+15×0.5°﹣15×6°=37.5°.
故答案为37.5°.
20.解:∵x+y=8,xy=12,
∴原式=(x+y)2﹣3xy=82﹣3×12=64﹣36=28.
故答案为28.
三.解答题(共7小题,满分60分)
21.解:(1)(2x)3(﹣5xy2)
=8x3?(﹣5xy2)
=﹣40x4y2;
(2)4(x+1)2﹣(2x+5)(2x﹣5)
=4(x2+2x+1)﹣(4x2﹣25)
=4x2+8x+4﹣4x2+25
=8x+29.
22.解:(1)6x2y(﹣2xy+y3)÷xy2,
=(﹣12x3y2+6x2y4)÷xy2
=﹣12x2+6xy2,
当x=2,y=﹣1时,
原式=﹣12×22+6×2×(﹣1)2
=﹣36;
(2)(x+2y)(x﹣2y)+(x﹣2y)2﹣(6x2y﹣2xy2)÷(2y)
=x2﹣4y2+x2﹣4xy+4y2﹣3x2+xy
=﹣x2﹣3xy,
当x=﹣2,y=时,
原式=﹣(﹣2)2﹣3×(﹣2)×
=﹣4+3
=﹣1.
23.解:∠AOD=180°﹣∠AOC=180°﹣50°=130°.
∠BOD=∠AOC=50°,
∠2=∠BOD﹣∠1=50°﹣20°=30°.
答:∠AOD和∠2的度数分别为130°和30°.
24.解:(1)在这个变化过程中,自变量是猕猴桃的销量,因变量是猕猴桃的销售额,
故答案为:猕猴桃的销量,猕猴桃的销售额;
(2)猕猴桃的销售额y(元)与销售量x(千克)之间的关系式为y=6x,
故答案为:y=6x;
(3)将x=100代入y=6x,可得y=6×100=600,
答:当猕猴桃销售量为100千克时,销售额是600元.
25.解:(1)10÷10%=100(人),即m=100,
“网购”人数;100×15%=15(人),
“支付宝”人数:100﹣40﹣15﹣10=35(人),35÷100=35%,因此n=35,
故答案为:100,35;
(2)补全条形统计图如图所示:
(3)1800×=1350(人),
答:全校1800名学生中,最认可“微信”和“支付宝”这两样新生事物的大约有1350人.
26.解:(1)DG与AB平行.理由:
∵EF∥DB,
∴∠1=∠D.
∵∠1=∠2,
∴∠D=∠2.
∴DG∥AB.
(2)∵EC平分∠FED,
∴∠DEC=∠DEF.
∵∠1=52°,
∴∠DEF=180°﹣∠1=128°.
∴∠DEC=∠DEF=64°.
∵DG∥AB,
∴∠C=∠DEC=64°.
27.解:(1)由图象可知,体育场离小明家2.5千米.
故答案为:2.5;
(2)由图象可知,小明在文具店逗留了:65﹣45=20(分钟).
故答案为:20;
(3)1.5÷=(km/h),
即小明从文具店到家的速度为km/h.
故答案为:.
同课章节目录
