2020-2021学年北师大版七年级数学下册第四章4.2图形的全等同步测试(word解析版)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第四章4.2图形的全等同步测试(word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 192.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 00:00:00 | ||
图片预览


文档简介
北师大版七年级数学下册第四章4.2图形的全等
同步测试(原卷版)
一.选择题
1.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
2.如图所示的2×2正方形网格中,∠1+∠2等于( )
A.105°
B.90°
C.85°
D.95°
3.下列判断正确的个数是( )
①两个正方形一定是全等图形;②三角形的一个外角一定大于与它不相邻的一个内角;
③三角形的三条高交于同一点;④两边和一角对应相等的两个三角形全等.
A.1个
B.2个
C.3个
D.4个
4.如图为正方形网格,则∠1+∠2+∠3=( )
A.105°
B.120°
C.115°
D.135°
5.下列说法中,错误的是( )
A.全等三角形对应角相等
B.全等三角形对应边相等
C.全等三角形的面积相等
D.面积相等的两个三角形一定全等
6.已知△ABC的边长均为整数,且最大边的边长为4,那么符合条件的不全等的三角形最多有( )
A.4个
B.5个
C.6个
D.7个
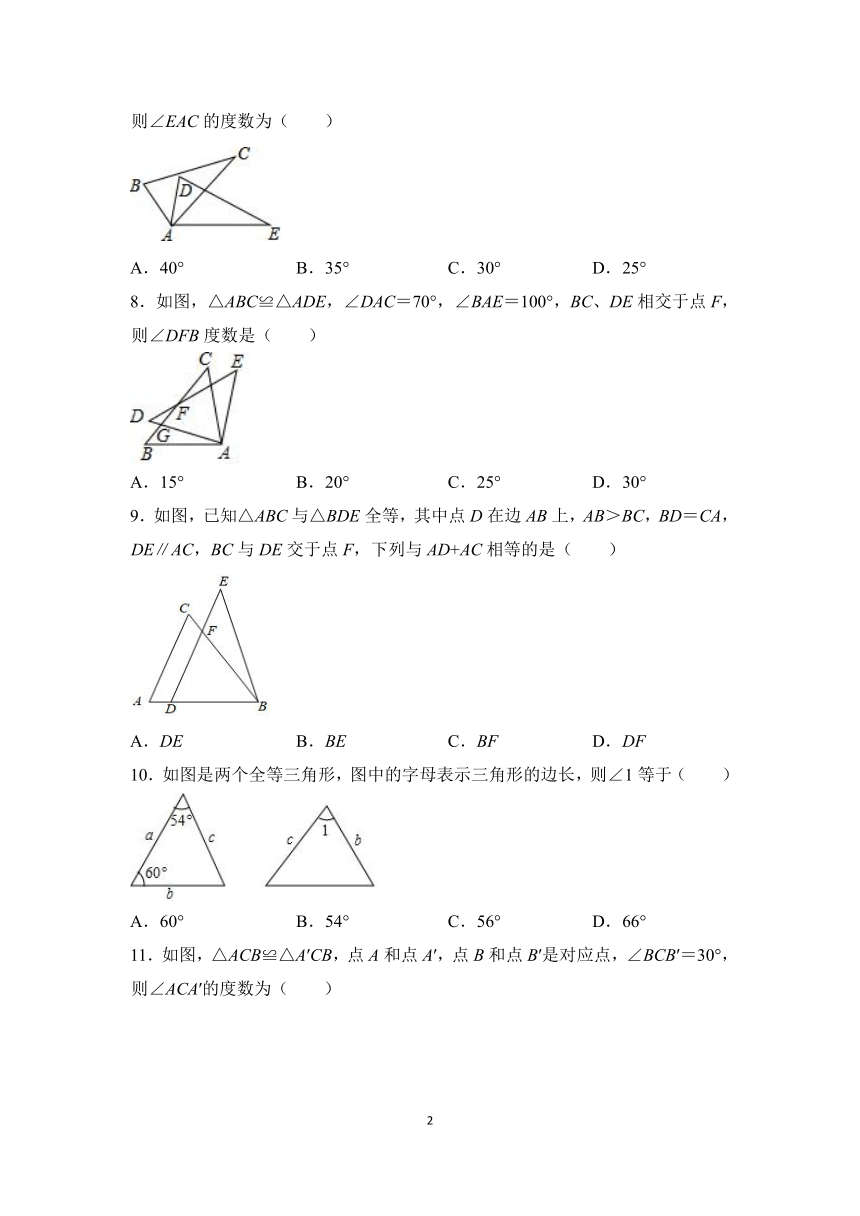
7.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
8.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A.15°
B.20°
C.25°
D.30°
9.如图,已知△ABC与△BDE全等,其中点D在边AB上,AB>BC,BD=CA,DE∥AC,BC与DE交于点F,下列与AD+AC相等的是( )
A.DE
B.BE
C.BF
D.DF
10.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于( )
A.60°
B.54°
C.56°
D.66°
11.如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
A.20°
B.30°
C.35°
D.40°
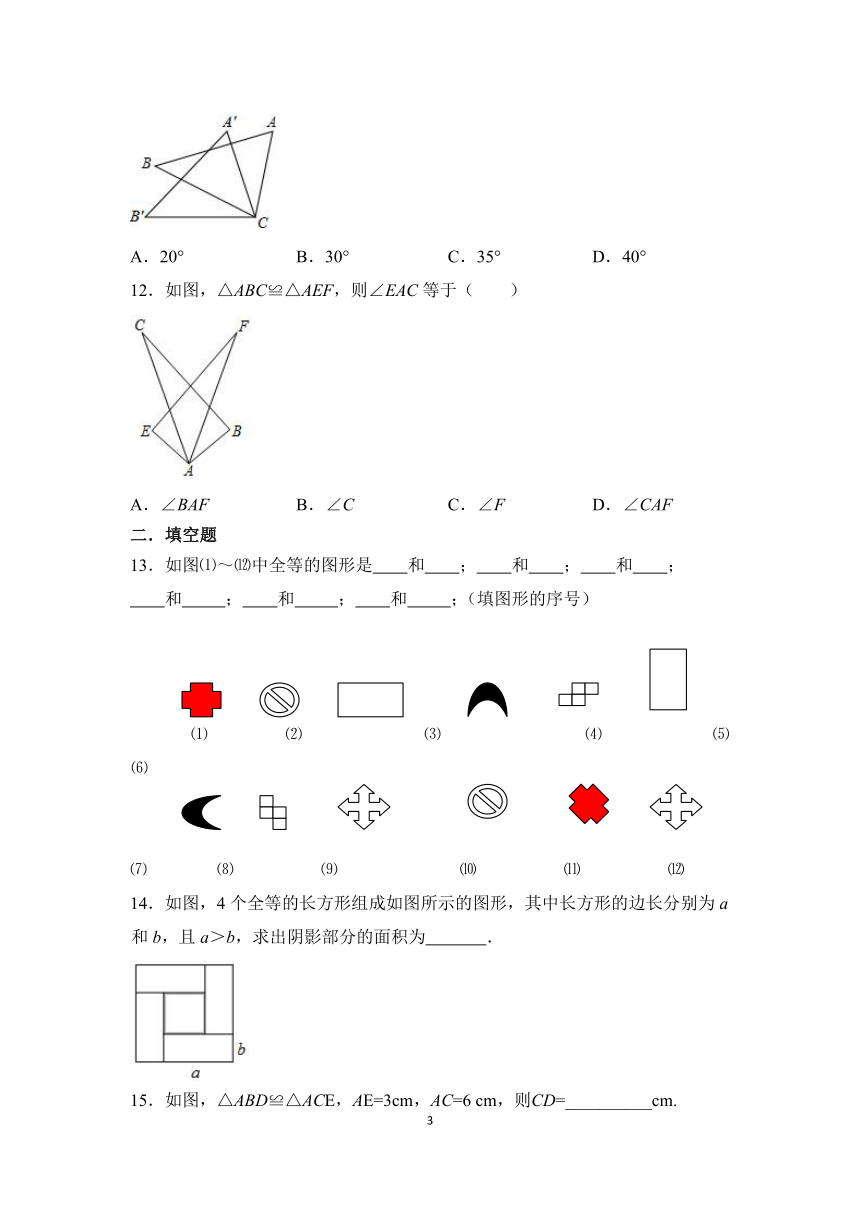
12.如图,△ABC≌△AEF,则∠EAC等于( )
A.∠BAF
B.∠C
C.∠F
D.∠CAF
二.填空题
13.如图⑴~⑿中全等的图形是
和
;
和
;
和
;
和
;
和
;
和
;(填图形的序号)
⑴
⑵
⑶
⑷
⑸
⑹
⑺ ⑻ ⑼ ⑽ ⑾ ⑿
14.如图,4个全等的长方形组成如图所示的图形,其中长方形的边长分别为a和b,且a>b,求出阴影部分的面积为
.
15.如图,△ABD≌△ACE,AE=3cm,AC=6
cm,则CD=__________cm.
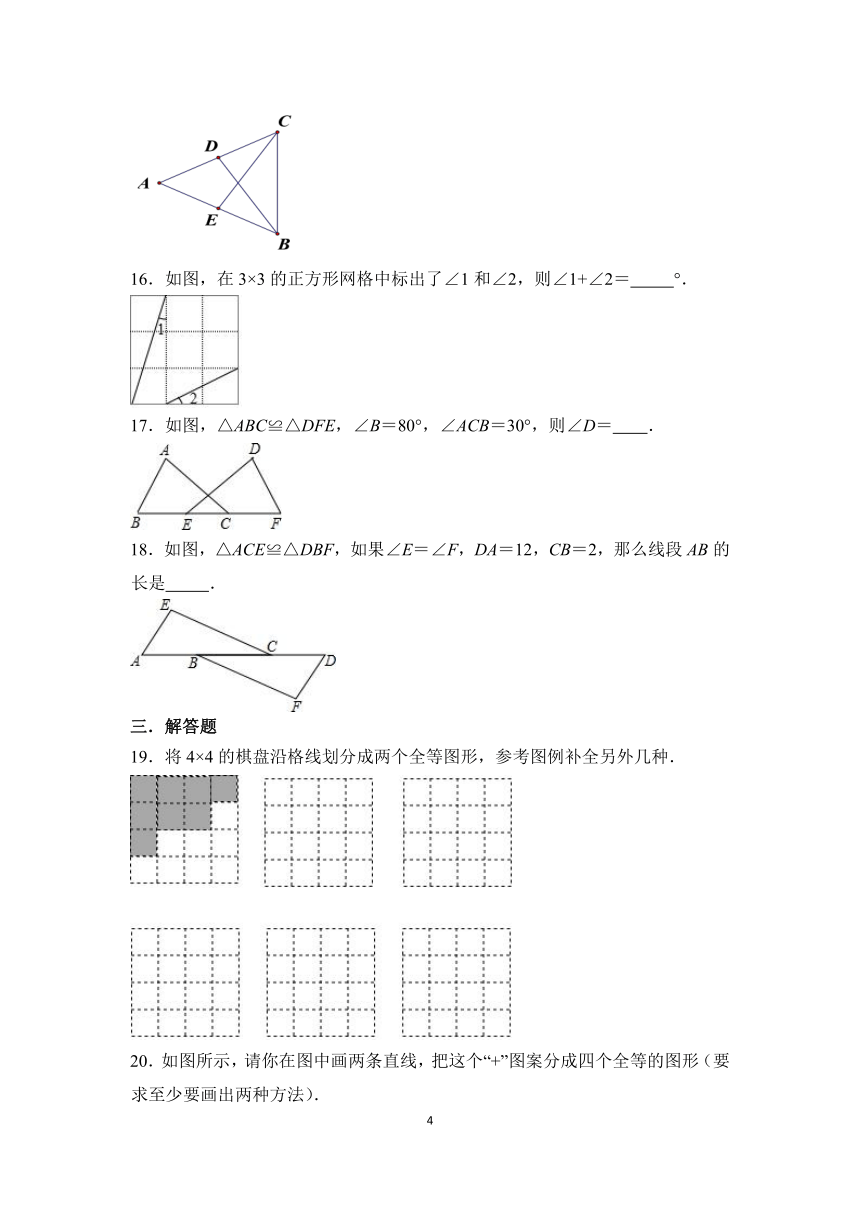
16.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=
°.
17.如图,△ABC≌△DFE,∠B=80°,∠ACB=30°,则∠D= .
18.如图,△ACE≌△DBF,如果∠E=∠F,DA=12,CB=2,那么线段AB的长是
.
三.解答题
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
21.如图,一块土地上共有20棵果树,要把它们平均分给四个小组去种植,并且要求每个小组分得的果树组成的图形、形状大小要相同,应该怎样分?
22.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
23.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
24.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是 ①②④ .(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
北师大版七年级数学下册第四章4.2图形的全等
同步测试答案提示
一.选择题
1.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
解:A、两个图形是全等图形,不符合题意;B、两个是全等图形,不符合题意;
C、两个图形大小不同,不是全等图形,符合题意;D、两个图形是全等图形,不符合题意;故选:C.
2.如图所示的2×2正方形网格中,∠1+∠2等于( )
A.105°
B.90°
C.85°
D.95°
解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
3.下列判断正确的个数是( )
①两个正方形一定是全等图形;②三角形的一个外角一定大于与它不相邻的一个内角;
③三角形的三条高交于同一点;④两边和一角对应相等的两个三角形全等.
A.1个
B.2个
C.3个
D.4个
解:①两个正方形不一定是全等图形,故错误;
②三角形的一个外角一定大于与它不相邻的一个内角,正确;
③三角形的三条高所在直线交于同一点,故错误;
④两边和一角对应相等的两个三角形不一定全等,故错误.
故选:A.
4.如图为正方形网格,则∠1+∠2+∠3=( )
A.105°
B.120°
C.115°
D.135°
解:∵在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴∠4=∠3,
∵∠1+∠4=90°,
∴∠1+∠3=90°,
∵AD=MD,∠ADM=90°,
∴∠2=45°,
∴∠1+∠2+∠3=135°,
故选:D.
5.下列说法中,错误的是( )
A.全等三角形对应角相等
B.全等三角形对应边相等
C.全等三角形的面积相等
D.面积相等的两个三角形一定全等
解:A、全等三角形对应角相等,说法正确;
B、全等三角形对应边相等,说法正确;
C、全等三角形的面积相等,说法正确;
D、面积相等的两个三角形一定全等,说法错误,例如一边长为6,这边上的高为3和一边长为3,这边上的高为6的两个三角形,面积相等,却不全等;
故选:D.
6.已知△ABC的边长均为整数,且最大边的边长为4,那么符合条件的不全等的三角形最多有( )
A.4个
B.5个
C.6个
D.7个
解:由于三角形的边长均为整数,且最大边的边长为4,
则三边的长为1,2,3,4四个数中某个或某几个,而1+2=3,1+3=4,
所以三条边不等的组合只能为2,3,4;
当是等腰三角形时只能为3,3,4;3,4,4;2,4,4;1,4,4组成;
当是等边三角形时边可以为4,4,4.
∴符合条件的不全等的三角形最多有6个.
故选:C.
7.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠EAC=∠BAD=70°﹣35°=35°,
故选:B.
8.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A.15°
B.20°
C.25°
D.30°
解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE,
又∠BAD=∠BAC﹣∠CAD,∠CAE=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵∠DAC=70°,∠BAE=100°,
∴∠BAD=(∠BAE﹣∠DAC)=(100°﹣70°)=15°,
在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=15°.
故选:A.
9.如图,已知△ABC与△BDE全等,其中点D在边AB上,AB>BC,BD=CA,DE∥AC,BC与DE交于点F,下列与AD+AC相等的是( )
A.DE
B.BE
C.BF
D.DF
解:∵DE∥AC,
∴∠A=∠EDB,
∵△ABC与△BDE全等,
∴BC=BE,AC=DB,AB=DE,
∴AC+AD=DB+AD=AB=DE,
故选:A.
10.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于( )
A.60°
B.54°
C.56°
D.66°
解:根据图形可知,两个全等三角形中,b,c的夹角为对应角
∴∠α=∠1
又∵∠α=180°﹣54°﹣60°=66°
∴∠1=66°
故选:D.
11.如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
A.20°
B.30°
C.35°
D.40°
解:∵△ACB≌△A′CB,
∴∠ACB=∠A′CB′,
∴∠ACA′+∠A′CB=∠A′CB+∠BCB′,
∴∠ACA′=∠BCB′=30°.
故选:B.
12.如图,△ABC≌△AEF,则∠EAC等于( )
A.∠BAF
B.∠C
C.∠F
D.∠CAF
解:∵△ABC≌△AEF,
∴∠CAB=∠FAE,
∴∠EAF﹣∠CAF=∠BAC﹣∠CAF,
∴∠CAE=∠FAB,
故选:A.
二.填空题
13.如图⑴~⑿中全等的图形是
和
;
和
;
和
;
和
;
和
;
和
;(填图形的序号)
⑴
⑵
⑶
⑷
⑸
⑹
⑺ ⑻ ⑼ ⑽ ⑾ ⑿
解:一个图形经过旋转、对称、翻折后并不改变图形的形状与大小.答案:(1)和(11);(2)和(10);(3)和(6);(4)和(7);(5)和(8);(9)和(12)
14.如图,4个全等的长方形组成如图所示的图形,其中长方形的边长分别为a和b,且a>b,求出阴影部分的面积为 (a﹣b)2 .
解:∵如图所示的图形是4个全等的长方形组成的图形,
∴阴影部分的边长为a﹣b的正方形,
∴阴影部分的面积=(a﹣b)2,
故答案为:(a﹣b)2.
15.如图,△ABD≌△ACE,AE=3cm,AC=6
cm,则CD=__________cm.
解:∵△ABD≌△ACE,
∴AD=AE=3
cm,
又AC=6
cm,
∴CD=AC-AD=3
cm
16.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= 45 °.
解:如图,∠2、∠3为两个全等三角形的对应角,
所以,∠2=∠3,
△ABC是等腰直角三角形,
所以,∠1+∠3=45°,
所以,∠1+∠2=45°.
故答案为:45.
17.如图,△ABC≌△DFE,∠B=80°,∠ACB=30°,则∠D= 70° .
解:∵∠B=80°,∠ACB=30°,
∴∠A=180°﹣80°﹣30°=70°,
∵△ABC≌△DFE,
∴∠D=∠A=70°,
故答案为:70°.
18.如图,△ACE≌△DBF,如果∠E=∠F,DA=12,CB=2,那么线段AB的长是 5 .
解:∵△ACE≌△DBF,DA=10,CB=2,
∴AB=CD===5.
故答案为:5.
三.解答题
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
解:如图所示,(答案不唯一)
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
解:如图所示:
21.如图,一块土地上共有20棵果树,要把它们平均分给四个小组去种植,并且要求每个小组分得的果树组成的图形、形状大小要相同,应该怎样分?
解:如图所示:
一共有20棵果树把它们平均分给四个小组去种植,每一个小组平均5棵,再根据条件“分得的果树组成的图形、形状大小要相同”进行分割即可.
22.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
23.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:假如BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
24.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是 ①②④ .(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
解:(1)符合要求的条件是①②④,
故答案为:①②④;
(2)选④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,
∵∠BCD=∠B′C′D′,
∴∠BCD﹣∠ACB=∠B′C′D′﹣∠A′C′B′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D,∠DAC=∠D′A′C′,DA=D′A′,
∴∠BAC+∠DAC=∠B′A′C′+∠D′A′C′,
即∠BAD=∠B′A′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同步测试(原卷版)
一.选择题
1.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
2.如图所示的2×2正方形网格中,∠1+∠2等于( )
A.105°
B.90°
C.85°
D.95°
3.下列判断正确的个数是( )
①两个正方形一定是全等图形;②三角形的一个外角一定大于与它不相邻的一个内角;
③三角形的三条高交于同一点;④两边和一角对应相等的两个三角形全等.
A.1个
B.2个
C.3个
D.4个
4.如图为正方形网格,则∠1+∠2+∠3=( )
A.105°
B.120°
C.115°
D.135°
5.下列说法中,错误的是( )
A.全等三角形对应角相等
B.全等三角形对应边相等
C.全等三角形的面积相等
D.面积相等的两个三角形一定全等
6.已知△ABC的边长均为整数,且最大边的边长为4,那么符合条件的不全等的三角形最多有( )
A.4个
B.5个
C.6个
D.7个
7.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
8.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A.15°
B.20°
C.25°
D.30°
9.如图,已知△ABC与△BDE全等,其中点D在边AB上,AB>BC,BD=CA,DE∥AC,BC与DE交于点F,下列与AD+AC相等的是( )
A.DE
B.BE
C.BF
D.DF
10.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于( )
A.60°
B.54°
C.56°
D.66°
11.如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
A.20°
B.30°
C.35°
D.40°
12.如图,△ABC≌△AEF,则∠EAC等于( )
A.∠BAF
B.∠C
C.∠F
D.∠CAF
二.填空题
13.如图⑴~⑿中全等的图形是
和
;
和
;
和
;
和
;
和
;
和
;(填图形的序号)
⑴
⑵
⑶
⑷
⑸
⑹
⑺ ⑻ ⑼ ⑽ ⑾ ⑿
14.如图,4个全等的长方形组成如图所示的图形,其中长方形的边长分别为a和b,且a>b,求出阴影部分的面积为
.
15.如图,△ABD≌△ACE,AE=3cm,AC=6
cm,则CD=__________cm.
16.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2=
°.
17.如图,△ABC≌△DFE,∠B=80°,∠ACB=30°,则∠D= .
18.如图,△ACE≌△DBF,如果∠E=∠F,DA=12,CB=2,那么线段AB的长是
.
三.解答题
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
21.如图,一块土地上共有20棵果树,要把它们平均分给四个小组去种植,并且要求每个小组分得的果树组成的图形、形状大小要相同,应该怎样分?
22.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
23.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
24.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是 ①②④ .(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
北师大版七年级数学下册第四章4.2图形的全等
同步测试答案提示
一.选择题
1.下列四个选项中,不是全等图形的是( )
A.
B.
C.
D.
解:A、两个图形是全等图形,不符合题意;B、两个是全等图形,不符合题意;
C、两个图形大小不同,不是全等图形,符合题意;D、两个图形是全等图形,不符合题意;故选:C.
2.如图所示的2×2正方形网格中,∠1+∠2等于( )
A.105°
B.90°
C.85°
D.95°
解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
3.下列判断正确的个数是( )
①两个正方形一定是全等图形;②三角形的一个外角一定大于与它不相邻的一个内角;
③三角形的三条高交于同一点;④两边和一角对应相等的两个三角形全等.
A.1个
B.2个
C.3个
D.4个
解:①两个正方形不一定是全等图形,故错误;
②三角形的一个外角一定大于与它不相邻的一个内角,正确;
③三角形的三条高所在直线交于同一点,故错误;
④两边和一角对应相等的两个三角形不一定全等,故错误.
故选:A.
4.如图为正方形网格,则∠1+∠2+∠3=( )
A.105°
B.120°
C.115°
D.135°
解:∵在△ABC和△AEF中,,
∴△ABC≌△AEF(SAS),
∴∠4=∠3,
∵∠1+∠4=90°,
∴∠1+∠3=90°,
∵AD=MD,∠ADM=90°,
∴∠2=45°,
∴∠1+∠2+∠3=135°,
故选:D.
5.下列说法中,错误的是( )
A.全等三角形对应角相等
B.全等三角形对应边相等
C.全等三角形的面积相等
D.面积相等的两个三角形一定全等
解:A、全等三角形对应角相等,说法正确;
B、全等三角形对应边相等,说法正确;
C、全等三角形的面积相等,说法正确;
D、面积相等的两个三角形一定全等,说法错误,例如一边长为6,这边上的高为3和一边长为3,这边上的高为6的两个三角形,面积相等,却不全等;
故选:D.
6.已知△ABC的边长均为整数,且最大边的边长为4,那么符合条件的不全等的三角形最多有( )
A.4个
B.5个
C.6个
D.7个
解:由于三角形的边长均为整数,且最大边的边长为4,
则三边的长为1,2,3,4四个数中某个或某几个,而1+2=3,1+3=4,
所以三条边不等的组合只能为2,3,4;
当是等腰三角形时只能为3,3,4;3,4,4;2,4,4;1,4,4组成;
当是等边三角形时边可以为4,4,4.
∴符合条件的不全等的三角形最多有6个.
故选:C.
7.如图,在△ABC中,∠B=80°,∠C=30°.若△ABC≌△ADE,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠EAC=∠BAD=70°﹣35°=35°,
故选:B.
8.如图,△ABC≌△ADE,∠DAC=70°,∠BAE=100°,BC、DE相交于点F,则∠DFB度数是( )
A.15°
B.20°
C.25°
D.30°
解:∵△ABC≌△ADE,
∴∠B=∠D,∠BAC=∠DAE,
又∠BAD=∠BAC﹣∠CAD,∠CAE=∠DAE﹣∠CAD,
∴∠BAD=∠CAE,
∵∠DAC=70°,∠BAE=100°,
∴∠BAD=(∠BAE﹣∠DAC)=(100°﹣70°)=15°,
在△ABG和△FDG中,∵∠B=∠D,∠AGB=∠FGD,
∴∠DFB=∠BAD=15°.
故选:A.
9.如图,已知△ABC与△BDE全等,其中点D在边AB上,AB>BC,BD=CA,DE∥AC,BC与DE交于点F,下列与AD+AC相等的是( )
A.DE
B.BE
C.BF
D.DF
解:∵DE∥AC,
∴∠A=∠EDB,
∵△ABC与△BDE全等,
∴BC=BE,AC=DB,AB=DE,
∴AC+AD=DB+AD=AB=DE,
故选:A.
10.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1等于( )
A.60°
B.54°
C.56°
D.66°
解:根据图形可知,两个全等三角形中,b,c的夹角为对应角
∴∠α=∠1
又∵∠α=180°﹣54°﹣60°=66°
∴∠1=66°
故选:D.
11.如图,△ACB≌△A′CB,点A和点A′,点B和点B′是对应点,∠BCB′=30°,则∠ACA′的度数为( )
A.20°
B.30°
C.35°
D.40°
解:∵△ACB≌△A′CB,
∴∠ACB=∠A′CB′,
∴∠ACA′+∠A′CB=∠A′CB+∠BCB′,
∴∠ACA′=∠BCB′=30°.
故选:B.
12.如图,△ABC≌△AEF,则∠EAC等于( )
A.∠BAF
B.∠C
C.∠F
D.∠CAF
解:∵△ABC≌△AEF,
∴∠CAB=∠FAE,
∴∠EAF﹣∠CAF=∠BAC﹣∠CAF,
∴∠CAE=∠FAB,
故选:A.
二.填空题
13.如图⑴~⑿中全等的图形是
和
;
和
;
和
;
和
;
和
;
和
;(填图形的序号)
⑴
⑵
⑶
⑷
⑸
⑹
⑺ ⑻ ⑼ ⑽ ⑾ ⑿
解:一个图形经过旋转、对称、翻折后并不改变图形的形状与大小.答案:(1)和(11);(2)和(10);(3)和(6);(4)和(7);(5)和(8);(9)和(12)
14.如图,4个全等的长方形组成如图所示的图形,其中长方形的边长分别为a和b,且a>b,求出阴影部分的面积为 (a﹣b)2 .
解:∵如图所示的图形是4个全等的长方形组成的图形,
∴阴影部分的边长为a﹣b的正方形,
∴阴影部分的面积=(a﹣b)2,
故答案为:(a﹣b)2.
15.如图,△ABD≌△ACE,AE=3cm,AC=6
cm,则CD=__________cm.
解:∵△ABD≌△ACE,
∴AD=AE=3
cm,
又AC=6
cm,
∴CD=AC-AD=3
cm
16.如图,在3×3的正方形网格中标出了∠1和∠2,则∠1+∠2= 45 °.
解:如图,∠2、∠3为两个全等三角形的对应角,
所以,∠2=∠3,
△ABC是等腰直角三角形,
所以,∠1+∠3=45°,
所以,∠1+∠2=45°.
故答案为:45.
17.如图,△ABC≌△DFE,∠B=80°,∠ACB=30°,则∠D= 70° .
解:∵∠B=80°,∠ACB=30°,
∴∠A=180°﹣80°﹣30°=70°,
∵△ABC≌△DFE,
∴∠D=∠A=70°,
故答案为:70°.
18.如图,△ACE≌△DBF,如果∠E=∠F,DA=12,CB=2,那么线段AB的长是 5 .
解:∵△ACE≌△DBF,DA=10,CB=2,
∴AB=CD===5.
故答案为:5.
三.解答题
19.将4×4的棋盘沿格线划分成两个全等图形,参考图例补全另外几种.
解:如图所示,(答案不唯一)
20.如图所示,请你在图中画两条直线,把这个“+”图案分成四个全等的图形(要求至少要画出两种方法).
解:如图所示:
21.如图,一块土地上共有20棵果树,要把它们平均分给四个小组去种植,并且要求每个小组分得的果树组成的图形、形状大小要相同,应该怎样分?
解:如图所示:
一共有20棵果树把它们平均分给四个小组去种植,每一个小组平均5棵,再根据条件“分得的果树组成的图形、形状大小要相同”进行分割即可.
22.如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠B=65°.
(1)求∠DCA的度数;
(2)若∠A=20°,求∠DFA的度数.
(1)证明:∵△ABC≌△DEC,
∴CB=CE,∠DCE=∠ACB,
∴∠CEB=∠B=65°,
在△BEC中,∠CEB+∠B+∠ECB=180°,
∴∠ECB=180°﹣65°﹣65°=50°,
又∠DCE=∠ACB,
∴∠DCA=∠ECB=50°;
(2)解:∵△ABC≌△DEC,
∴∠D=∠A=20°,
在△DFC中,
∠DFA=∠DCA+∠D=50°+20°=70°.
23.如图,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)求证:BD=DE+CE;
(2)请你猜想△ABD满足什么条件时,BD∥CE.
(1)证明:∵△BAD≌△ACE,
∴AD=CE,BD=AE,
∵A,D,E三点在同一直线上,
∴AE=AD+DE,
∴BD=CE+DE;
(2)解:假如BD∥CE,
则∠BDE=∠E,
∵△BAD≌△ACE,
∴∠ADB=∠E,
∴∠ADB=∠BDE,
又∵∠ADB+∠BDE=180°,
∴∠ADB=∠BDE=90°,
∴当∠ADB=∠E=90°时,BD∥CE.
24.我们知道能完全重合的图形叫做全等图形,因此,如果两个四边形能完全重合,那么这两个四边形全等,也就是说,当两个四边形的四个内角、四条边都分别对应相等时,这两个四边形全等.请借助三角形全等的知识,解决有关四边形全等的问题.
如图,已知,四边形ABCD和四边形A′B′C′D′中,AB=A′B′,BC=B′C′,∠B=∠B′,∠C=∠C′,现在只需补充一个条件,就可得四边形ABCD≌四边形A′B′C′D′.
下列四个条件:①∠A=∠A′;②∠D=∠D′;③AD=A′D′;④CD=C′D′
(1)其中,符合要求的条件是 ①②④ .(直接写出编号)
(2)选择(1)中的一个条件,证明四边形ABCD≌四边形A′B′C′D′.
解:(1)符合要求的条件是①②④,
故答案为:①②④;
(2)选④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,
∵∠BCD=∠B′C′D′,
∴∠BCD﹣∠ACB=∠B′C′D′﹣∠A′C′B′,
∴∠ACD=∠A′C′D′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D,∠DAC=∠D′A′C′,DA=D′A′,
∴∠BAC+∠DAC=∠B′A′C′+∠D′A′C′,
即∠BAD=∠B′A′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
