吉林省延边州二高北校区2020-2021学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 吉林省延边州二高北校区2020-2021学年高一下学期期中考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 16:51:45 | ||
图片预览


文档简介
延边二中北校区内试题
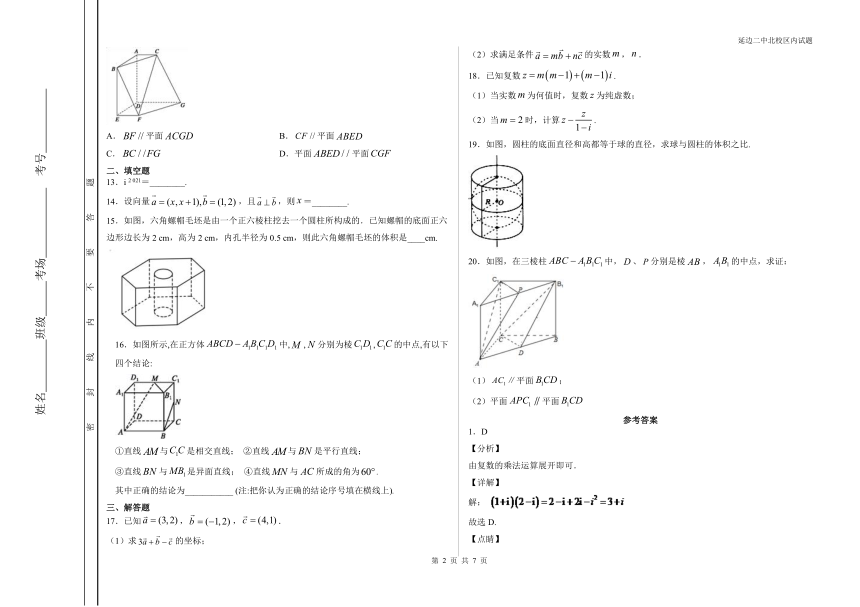
延边二中北校区(2020-2021)学年度下学期
高一年级 期中考试 数学试卷
本试卷共120分,考试时间120分钟。
一、单选题
1.( )
A. B. C. D.
2.设,则=( )
A.2 B. C. D.1
3.在复平面内,复数的共轭复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若,则( )
A. B. C. D.
5.圆锥的轴截面是边长为的正三角形,则圆锥的表面积为( )
A. B. C. D.
6.一个几何体的三视图及其尺寸如图(单位:),则该几何体的表面积为( )
A. B. C. D.
7.若直线和是异面直线,在平面内,在平面内,l是平面与平面的交线,则下列命题正确的是( )
A.与,都相交 B.与,都不相交
C.至少与,中的一条相交 D.至多与,中的一条相交
8.如图,正方体中,为棱的中点,用过点、、的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )
A. B.C. D.
9.已知点则与同方向的单位向量为( )
A. B. C. D.
10.平面向量与的夹角为60°,=(2,0),||=1,则等于( )
A. B.2 C.4 D.12
11.如图所示,已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )
A.a km B.a km C.a km D.2a km
12.如图,在多面体中,平面平面 ,且,则 ( )
A.平面 B.平面
C. D.平面平面
二、填空题
13.i 2 021=________.
14.设向量,且,则=________.
15.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是____cm.
16.如图所示,在正方体中,,分别为棱,的中点,有以下四个结论:
①直线与是相交直线; ②直线与是平行直线;
③直线与是异面直线; ④直线与所成的角为.
其中正确的结论为___________ (注:把你认为正确的结论序号填在横线上).
三、解答题
17.已知,,.
(1)求的坐标;
(2)求满足条件的实数,.
18.已知复数.
(1)当实数为何值时,复数为纯虚数;
(2)当时,计算.
19.如图,圆柱的底面直径和高都等于球的直径,求球与圆柱的体积之比.
20.如图,在三棱柱中,、分别是棱,的中点,求证:
(1)平面;
(2)平面平面
参考答案
1.D
【分析】
由复数的乘法运算展开即可.
【详解】
解:
故选D.
【点睛】
本题主要考查复数的四则运算,属于基础题.
2.C
【分析】
先由复数的除法运算(分母实数化),求得,再求.
【详解】
因为,所以,所以,故选C.
【点睛】
本题主要考查复数的乘法运算,复数模的计算.本题也可以运用复数模的运算性质直接求解.
3.D
【详解】
分析:将复数化为最简形式,求其共轭复数,找到共轭复数在复平面的对应点,判断其所在象限.
详解:的共轭复数为
对应点为,在第四象限,故选D.
点睛:此题考查复数的四则运算,属于送分题,解题时注意审清题意,切勿不可因简单导致马虎丢分.
4.D
【分析】
根据复数运算法则求解即可.
【详解】
.故选D.
【点睛】
本题考查复数的商的运算,渗透了数学运算素养.采取运算法则法,利用方程思想解题.
5.C
【分析】
根据圆锥轴截面的定义结合正三角形的性质,可得圆锥的底面半径、母线长,结合圆锥表面积公式,即可求出答案.
【详解】
圆锥的轴截面是边长为的正三角形,
圆锥的底面半径,母线长;
表面积
故选C.
【点睛】
本题给出圆锥轴截面的形状,求圆锥的表面积,着重考查了等边三角形的性质和圆锥轴截面等知识,属于基础题.
6.A
【详解】
分析:根据正视图,左视图,俯视图可得该几何体为圆柱,然后根据圆柱表面积公式求解即可.
详解:由题得该几何体为圆柱,底面半径为2,高为4,所以表面积为:
,
故选A.
点睛:考查三视图,能正确推理出几何体的形状是解题关键,属于基础题.
7.C
【详解】
试题分析:A.l与l1,l2可以相交,如图:
∴该选项错误;
B.l可以和l1,l2中的一个平行,如上图,∴该选项错误;
C.l可以和l1,l2都相交,如下图:
,∴该选项错误;
D.“l至少与l1,l2中的一条相交”正确,假如l和l1,l2都不相交;
∵l和l1,l2都共面;
∴l和l1,l2都平行;
∴l1∥l2,l1和l2共面,这样便不符合已知的l1和l2异面;
∴该选项正确.
故选D.
考点:点、线、面的位置关系.
8.A
【分析】
根据剩余几何体的直观图,结合三视图的定义即可得到主视图
【详解】
解:正方体中,
过点的平面截去该正方体的上半部分后,
剩余部分的直观图如图:
则该几何体的正视图为图中粗线部分.
故选A.
【点睛】
本题主要考查了空间三视图与直观图的应用问题,是基础题.
9.A
【详解】
试题分析:,所以与同方向的单位向量为,故选A.
考点:向量运算及相关概念.
10.B
【分析】
把平方后再开方即可.
【详解】
因为
所以
所以
故选:B.
11.B
【分析】
先根据题意确定的值,再由余弦定理可直接求得的值.
【详解】
在中知∠ACB=120°,由余弦定理得AB2=AC2+BC2-2AC·BCcos120°=2a2-2a2×=3a2,∴AB=a.
故选:B.
【点睛】
本题主要考查余弦定理的应用,属于基础题.
12.A
【解析】
【分析】
取DG的中点M,连AM、FM,证明四边形ABFM是平行四边形,问题得解.
【详解】
如图所示,取DG的中点M,连AM、FM,.
则由已知条件易证得四边形DEFM是平行四边形,
∴且.
∵平面ABC∥平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,
∴AB∥DE,
∴AB∥FM.
又AB=DE,
∴AB=FM,
∴四边形ABFM是平行四边形,
∴BF∥AM.
又BF平面ACGD,AM平面ACGD,
∴BF∥平面ACGD.选A.
【点睛】
本题主要考查了线面平行的判定定理及面面平行的性质,还考查了转化能力及空间思维能力,属于中档题.
13.
【分析】
利用周期性求得所求表达式的值.
【详解】
故答案为:
14.
【详解】
根据两向量垂直,可得,
解得.
故答案为:.
15.
【分析】
先求正六棱柱体积,再求圆柱体积,相减得结果.
【详解】
正六棱柱体积为
圆柱体积为
所求几何体体积为
故答案为:
【点睛】
本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.
16.③④.
【分析】
根据异面直线判定定理可知①错误,③正确;根据线线平行的性质可知②错误;通过平移求解出异面直线所成角,可得④正确.
【详解】
①平面,平面,平面,,可知与为异面直线,故①错误;
②,,可知与不平行,故②错误;
③平面,平面,平面,,可知与异面,可知③正确;
④,分别为棱,的中点,可知,则直线与所成角即为,又为等比三角形,可得,可知④正确.
本题正确结果:③④
【点睛】
本题考查空间中直线与直线的位置关系、异面直线所成角的求解问题,属于基础题.
17.(1),;(2).
【分析】
(1)利用向量的坐标运算即可求的坐标.
(2)由已知线性关系,结合坐标表示得到,解方程组即可.
【详解】
(1)根据题意,,,,
则,,,,,
(2)根据题意,若,即,,,,
则有,解可得,
故.
18.(1);(2).
【分析】
(1)由复数为纯虚数得出其实部为零,虚部不为零,进而可解得实数的值;
(2)当时,由复数的四则运算法则可计算得出的值.
【详解】
(1)复数为纯虚数,则,解得;
(2)当时,,
.
【点睛】
本题考查利用复数类型求参数,同时也考查了复数的计算,考查计算能力,属于基础题.
19.
【分析】
利用圆柱和球的体积公式,求出体积即可.
【详解】
解:设球的半径为R,则圆柱的底面半径为R,高为2R.
球的体积,圆柱的体积,
.
【点睛】
本题考查圆柱和球的体积,是基础题.
20.(1)见证明;(2)见证明
【分析】
(1)设与的交点为,连结,证明,再由线面平行的判定可得平面;
(2)由为线段的中点,点是的中点,证得四边形为平行四边形,得到,进一步得到平面.再由平面,结合面面平行的判定可得平面平面.
【详解】
证明:(1)设与的交点为,连结,
∵四边形为平行四边形,∴为中点,
又是的中点,∴是三角形的中位线,则,
又∵平面,平面,
∴平面;
(2)∵为线段的中点,点是的中点,
∴且,则四边形为平行四边形,
∴,
又∵平面,平面,
∴平面.
又平面,,且平面,平面,
∴平面平面.
【点睛】
本题考查直线与平面,平面与平面平行的判定,考查空间想象能力与思维能力,是中档题.
延边二中北校区(2020-2021)学年度下学期
高一年级 期中考试 数学试卷
本试卷共120分,考试时间120分钟。
一、单选题
1.( )
A. B. C. D.
2.设,则=( )
A.2 B. C. D.1
3.在复平面内,复数的共轭复数对应的点位于( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.若,则( )
A. B. C. D.
5.圆锥的轴截面是边长为的正三角形,则圆锥的表面积为( )
A. B. C. D.
6.一个几何体的三视图及其尺寸如图(单位:),则该几何体的表面积为( )
A. B. C. D.
7.若直线和是异面直线,在平面内,在平面内,l是平面与平面的交线,则下列命题正确的是( )
A.与,都相交 B.与,都不相交
C.至少与,中的一条相交 D.至多与,中的一条相交
8.如图,正方体中,为棱的中点,用过点、、的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )
A. B.C. D.
9.已知点则与同方向的单位向量为( )
A. B. C. D.
10.平面向量与的夹角为60°,=(2,0),||=1,则等于( )
A. B.2 C.4 D.12
11.如图所示,已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )
A.a km B.a km C.a km D.2a km
12.如图,在多面体中,平面平面 ,且,则 ( )
A.平面 B.平面
C. D.平面平面
二、填空题
13.i 2 021=________.
14.设向量,且,则=________.
15.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm,高为2 cm,内孔半径为0.5 cm,则此六角螺帽毛坯的体积是____cm.
16.如图所示,在正方体中,,分别为棱,的中点,有以下四个结论:
①直线与是相交直线; ②直线与是平行直线;
③直线与是异面直线; ④直线与所成的角为.
其中正确的结论为___________ (注:把你认为正确的结论序号填在横线上).
三、解答题
17.已知,,.
(1)求的坐标;
(2)求满足条件的实数,.
18.已知复数.
(1)当实数为何值时,复数为纯虚数;
(2)当时,计算.
19.如图,圆柱的底面直径和高都等于球的直径,求球与圆柱的体积之比.
20.如图,在三棱柱中,、分别是棱,的中点,求证:
(1)平面;
(2)平面平面
参考答案
1.D
【分析】
由复数的乘法运算展开即可.
【详解】
解:
故选D.
【点睛】
本题主要考查复数的四则运算,属于基础题.
2.C
【分析】
先由复数的除法运算(分母实数化),求得,再求.
【详解】
因为,所以,所以,故选C.
【点睛】
本题主要考查复数的乘法运算,复数模的计算.本题也可以运用复数模的运算性质直接求解.
3.D
【详解】
分析:将复数化为最简形式,求其共轭复数,找到共轭复数在复平面的对应点,判断其所在象限.
详解:的共轭复数为
对应点为,在第四象限,故选D.
点睛:此题考查复数的四则运算,属于送分题,解题时注意审清题意,切勿不可因简单导致马虎丢分.
4.D
【分析】
根据复数运算法则求解即可.
【详解】
.故选D.
【点睛】
本题考查复数的商的运算,渗透了数学运算素养.采取运算法则法,利用方程思想解题.
5.C
【分析】
根据圆锥轴截面的定义结合正三角形的性质,可得圆锥的底面半径、母线长,结合圆锥表面积公式,即可求出答案.
【详解】
圆锥的轴截面是边长为的正三角形,
圆锥的底面半径,母线长;
表面积
故选C.
【点睛】
本题给出圆锥轴截面的形状,求圆锥的表面积,着重考查了等边三角形的性质和圆锥轴截面等知识,属于基础题.
6.A
【详解】
分析:根据正视图,左视图,俯视图可得该几何体为圆柱,然后根据圆柱表面积公式求解即可.
详解:由题得该几何体为圆柱,底面半径为2,高为4,所以表面积为:
,
故选A.
点睛:考查三视图,能正确推理出几何体的形状是解题关键,属于基础题.
7.C
【详解】
试题分析:A.l与l1,l2可以相交,如图:
∴该选项错误;
B.l可以和l1,l2中的一个平行,如上图,∴该选项错误;
C.l可以和l1,l2都相交,如下图:
,∴该选项错误;
D.“l至少与l1,l2中的一条相交”正确,假如l和l1,l2都不相交;
∵l和l1,l2都共面;
∴l和l1,l2都平行;
∴l1∥l2,l1和l2共面,这样便不符合已知的l1和l2异面;
∴该选项正确.
故选D.
考点:点、线、面的位置关系.
8.A
【分析】
根据剩余几何体的直观图,结合三视图的定义即可得到主视图
【详解】
解:正方体中,
过点的平面截去该正方体的上半部分后,
剩余部分的直观图如图:
则该几何体的正视图为图中粗线部分.
故选A.
【点睛】
本题主要考查了空间三视图与直观图的应用问题,是基础题.
9.A
【详解】
试题分析:,所以与同方向的单位向量为,故选A.
考点:向量运算及相关概念.
10.B
【分析】
把平方后再开方即可.
【详解】
因为
所以
所以
故选:B.
11.B
【分析】
先根据题意确定的值,再由余弦定理可直接求得的值.
【详解】
在中知∠ACB=120°,由余弦定理得AB2=AC2+BC2-2AC·BCcos120°=2a2-2a2×=3a2,∴AB=a.
故选:B.
【点睛】
本题主要考查余弦定理的应用,属于基础题.
12.A
【解析】
【分析】
取DG的中点M,连AM、FM,证明四边形ABFM是平行四边形,问题得解.
【详解】
如图所示,取DG的中点M,连AM、FM,.
则由已知条件易证得四边形DEFM是平行四边形,
∴且.
∵平面ABC∥平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,
∴AB∥DE,
∴AB∥FM.
又AB=DE,
∴AB=FM,
∴四边形ABFM是平行四边形,
∴BF∥AM.
又BF平面ACGD,AM平面ACGD,
∴BF∥平面ACGD.选A.
【点睛】
本题主要考查了线面平行的判定定理及面面平行的性质,还考查了转化能力及空间思维能力,属于中档题.
13.
【分析】
利用周期性求得所求表达式的值.
【详解】
故答案为:
14.
【详解】
根据两向量垂直,可得,
解得.
故答案为:.
15.
【分析】
先求正六棱柱体积,再求圆柱体积,相减得结果.
【详解】
正六棱柱体积为
圆柱体积为
所求几何体体积为
故答案为:
【点睛】
本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.
16.③④.
【分析】
根据异面直线判定定理可知①错误,③正确;根据线线平行的性质可知②错误;通过平移求解出异面直线所成角,可得④正确.
【详解】
①平面,平面,平面,,可知与为异面直线,故①错误;
②,,可知与不平行,故②错误;
③平面,平面,平面,,可知与异面,可知③正确;
④,分别为棱,的中点,可知,则直线与所成角即为,又为等比三角形,可得,可知④正确.
本题正确结果:③④
【点睛】
本题考查空间中直线与直线的位置关系、异面直线所成角的求解问题,属于基础题.
17.(1),;(2).
【分析】
(1)利用向量的坐标运算即可求的坐标.
(2)由已知线性关系,结合坐标表示得到,解方程组即可.
【详解】
(1)根据题意,,,,
则,,,,,
(2)根据题意,若,即,,,,
则有,解可得,
故.
18.(1);(2).
【分析】
(1)由复数为纯虚数得出其实部为零,虚部不为零,进而可解得实数的值;
(2)当时,由复数的四则运算法则可计算得出的值.
【详解】
(1)复数为纯虚数,则,解得;
(2)当时,,
.
【点睛】
本题考查利用复数类型求参数,同时也考查了复数的计算,考查计算能力,属于基础题.
19.
【分析】
利用圆柱和球的体积公式,求出体积即可.
【详解】
解:设球的半径为R,则圆柱的底面半径为R,高为2R.
球的体积,圆柱的体积,
.
【点睛】
本题考查圆柱和球的体积,是基础题.
20.(1)见证明;(2)见证明
【分析】
(1)设与的交点为,连结,证明,再由线面平行的判定可得平面;
(2)由为线段的中点,点是的中点,证得四边形为平行四边形,得到,进一步得到平面.再由平面,结合面面平行的判定可得平面平面.
【详解】
证明:(1)设与的交点为,连结,
∵四边形为平行四边形,∴为中点,
又是的中点,∴是三角形的中位线,则,
又∵平面,平面,
∴平面;
(2)∵为线段的中点,点是的中点,
∴且,则四边形为平行四边形,
∴,
又∵平面,平面,
∴平面.
又平面,,且平面,平面,
∴平面平面.
【点睛】
本题考查直线与平面,平面与平面平行的判定,考查空间想象能力与思维能力,是中档题.
同课章节目录
