吉林省延边州二高北校区2020-2021学年高二下学期期中考试文科数学试题 Word版含答案
文档属性
| 名称 | 吉林省延边州二高北校区2020-2021学年高二下学期期中考试文科数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 16:52:29 | ||
图片预览



文档简介
延边二中北校区内部试题
延边二中北校区(2020-2021)学年度上学期高二年级 期中考试 文科数学试卷
分卷I
一、单选题
1.函数在到之间的平均变化率为( )
A. B. C. D.
2.若(m为常数),则等于( )
A. B.1 C.m D.
3.在曲线上切线的倾斜角为的点的坐标为( )
A. B. C. D.或
4.若函数,则( )
A. B.1 C. D.3
5.下列求导结果正确的是( )
A. B.
C. D.
6.已知函数的导函数为,若的图象如图所示,则函数的图象可能是( )
A. B. C. D.
7.函数在处取得极值,则( )
A.,且为极大值点 B.,且为极小值点
C.,且为极大值点 D.,且为极小值点
8.设函数,则f(x)是( )
A.有一个零点的增函数 B.有一个零点的减函数
C.有二个零点的增函数 D.没有零点的减函数
9.已知两个变量,之间具有相关关系,现选用,,,四个模型得到相应的回归方程,并计算得到了相应的值分别为,,,,那么拟合效果最好的模型为
A. B. C. D.
10.在某次飞行航程中遭遇恶劣气候,55名男乘客中有24名晕机,34名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用的数据分析方法应是
A.频率分布直方图 B.回归分析 C.独立性检验 D.用样本估计总体
11.下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程,变量x增加一个单位时,y平均增加5个单位;③线性回归直线必过;
④曲线上的点与该点的坐标之间具有相关关系;⑤在一个2×2列联表中,由计算得K2=13.079.则其两个变量间有关系的可能性是90%.其中错误的个数是
A.1 B.2 C.3 D.4
12.已知,对,且,恒有,则实数的取值范围是( )
A. B. C. D.
二、填空题
13.若有一组数据的总偏差平方和为100,相关指数=0.75,则其残差平方和为_______.
14.已知数据点(xi,yi)(i=1,2,3,…,n)在一条直线上,则相关系数r=________.
15.已知函数有三个零点,则实数的取值范围是__________.
16.在吸烟与患肺病是否相关的判断中,有下面的说法:
(1)从独立性分析可知在犯错误的概率不超过0.05的前提下,认为吸烟与患肺病有关系时,是指有的可能性使得推断错误.(2)从独立性分析可知在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系时,若某人吸烟,则他有的可能患有肺病;(3)若,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;其中说法正确的是________.
三、解答题
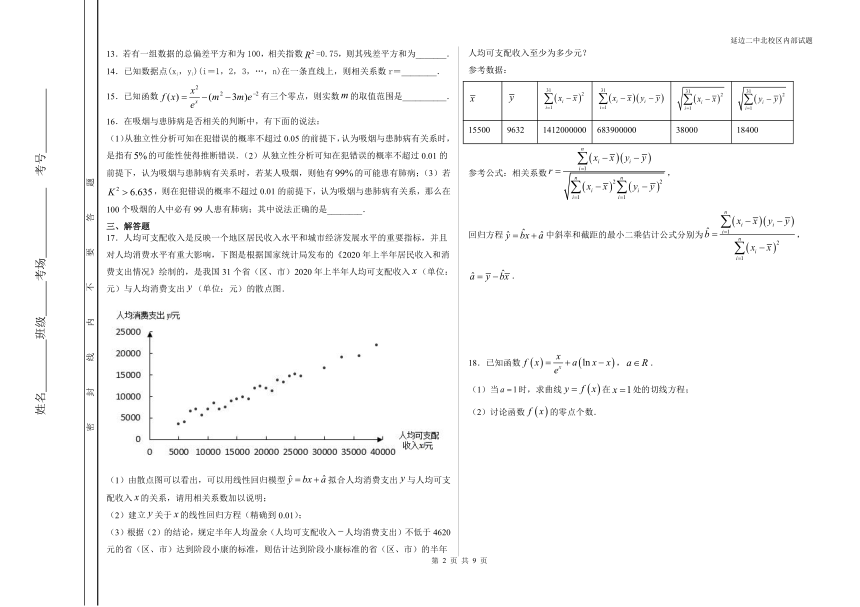
17.人均可支配收入是反映一个地区居民收入水平和城市经济发展水平的重要指标,并且对人均消费水平有重大影响,下图是根据国家统计局发布的《2020年上半年居民收入和消费支出情况》绘制的,是我国31个省(区、市)2020年上半年人均可支配收入(单位:元)与人均消费支出(单位:元)的散点图.
(1)由散点图可以看出,可以用线性回归模型拟合人均消费支出与人均可支配收入的关系,请用相关系数加以说明;
(2)建立关于的线性回归方程(精确到0.01);
(3)根据(2)的结论,规定半年人均盈余(人均可支配收入人均消费支出)不低于4620元的省(区、市)达到阶段小康的标准,则估计达到阶段小康标准的省(区、市)的半年人均可支配收入至少为多少元?
参考数据:
15500 9632 1412000000 683900000 38000 18400
参考公式:相关系数,
回归方程中斜率和截距的最小二乘估计公式分别为,.
18.已知函数,.
(1)当时,求曲线在处的切线方程;
(2)讨论函数的零点个数.
19.已知函数(为实数).
(1)若,求的最小值;
(2)若恒成立,求的取值范围.
20.随着手机的日益普及,学生使用手机对学校管理和学生发展带来诸多不利影响.为保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏,促进学生身心健康发展,教育部于2021年1月15日下发文件《关于加强中小学生手机管理工作的通知》,对中小学生的手机使用和管理作出了相关的规定某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,对我校80名学生调查得到部分统计数据如下表,记为事件:“学习成绩优秀且不使用手机”;为事件:“学习成绩不优秀且不使用手机”,且已知事件的频率是事件的频率的2倍.
不使用手机 使用手机 合计
学习成绩优秀人数
12
学习成绩不优秀人数
26
合计
(1)求表中,的值,并补全表中所缺数据;
(2)运用独立性检验思想,判断是否有99.5%的把握认为中学生使用手机对学习有影响?
参考数据:,其中.
0.10 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考答案
1.B
【分析】
直接代入平均变化率公式即得解.
【详解】
,
所以.
故选:B
【点睛】
本题主要考查平均变化率的计算,意在考查学生对该知识的理解掌握水平,属于基础题.
2.D
【分析】
根据导数的概念,直接计算,即可得出结果.
【详解】
由题意,根据导数的概念可得,
,
所以.
故选:D.
3.D
【分析】
利用导数的几何意义可求得结果.
【详解】
设所求点为,
因为,所以,因为切线的倾斜角为,所以切线斜率为,
即,所以,
则当时,;当时,,
所以所求点坐标为或.
故选:D
4.C
【分析】
求得导函数,代入即可求得结果.
【详解】
,则.
故选:C
5.C
【分析】
利用导数的求导法则以及复合函数的求导法则可判断各选项的正误.
【详解】
对于A选项,,A选项错误;
对于B选项,,B选项错误;
对于C选项,,C选项正确;
对于D选项,,D选项错误.
故选:C.
6.D
【分析】
根据导函数大于,原函数单调递增;导函数小于,原函数单调递减;即可得出正确答案.
【详解】
由导函数得图象可得:时,,所以在单调递减,
排除选项A、B,
当时,先正后负,所以在先增后减,
因选项C是先减后增再减,故排除选项C,
故选:D.
7.B
【分析】
先求导,再根据题意得,由此求得,再根据导数研究函数的极值.
【详解】
解:∵,
∴,
又在处取得极值,
∴,得,
∴,
由得,,即,
∴,即,
同理,由得,,
∴在处附近的左侧为负,右侧为正,
∴函数在处取得极小值,
故选:B.
【点睛】
本题主要考查利用函数的导数研究函数的单调性与极值,属于基础题.
8.A
【分析】
求导,由导数与单调性的关系判断增减性,利用零点存在定理判断零点所在区间,结合单调性即可判断零点个数.
【详解】
,则,
所以函数是定义域为上的连续的增函数,
又,,
零点存在定理可得在上存在唯一零点.
故选:.
【点睛】
本题考查了利用导数研究函数的单调性及函数零点的判定定理,属于基础题.
9.B
【详解】
越大,拟合效果越好,故选.
10.C
【详解】
根据题意,结合题目中的数据,列出2×2列联表,求出观测值K2,对照数表可得出概率结论,这种分析数据的方法是独立性检验.
本题选择C选项.
11.C
【详解】
对于①,方差反映一组数据的波动大小,将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变,故正确;对于②,一个回归方程,变量增加一个单位时,平均减小5个单位,故不正确;对于③,线性回归直线必过样本中心点,故正确;对于④,曲线上的点与该点的坐标之间具有一一对应关系,故不正确;对于⑤,有一个2×2列联表中,由计算得,则其两个变量间有关系的可能性是99.9%,故不正确.
故选C.
12.B
【分析】
依题意,得在上单调递增,转化为恒成立,则,令,利用的单调性可得答案.
【详解】
依题意,得,且,
,所以,
则在上单调递增,则,
恒成立,则,令,则,当时;当时,,
故,所以,
故选:B.
【点睛】
解题的关键点是含有参数的不等式恒成立的问题,可以进行参数分离,再构造函数,考查了学生分析问题、解决问题的能力.
13.25
【解析】
因为数据的总偏差平方和为,相关指数,,,故答案为.
14.±1
【分析】
由题意,数据点在一条直线上,可知相关系数的值,得到答案.
【详解】
由题易知,相关系数r=±1.
【点睛】
本题主要考查了相关性的应用,其中熟记相关系数的含义是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
15.
【分析】
将问题转化为直线与函数的图象有三个交点,利用导数分析函数的单调性可求得的取值范围.
【详解】
构造,,有三个零点即与有三个交点,
,在和上单调递减,在上单调递增,
且,,即,
即,解得.
故答案为:.
【点睛】
本题考查利用函数的零点个数求参数,关键点是将问题转化为直线与函数的图象有三个交点,同时也考查了导数的应用,属于中等题.
16.(1)
【分析】
根据题意,利用独立性检验的定义与基本思想,对题目中的命题进行逐个分析、判断,即可求解出答案.
【详解】
根据独立性检验的基本思想,在犯错误的概率不超过0.05的前提下,认为吸烟与患肺病有关系的意思为有的把握认为这个推理是正确的,所以(1)正确.从独立性分析可知在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系的意思为有的把握认为这个推理是正确的,而不是说某个人吸烟就有的可能患有肺病,所以(2)错误.同(2)中的推论,所以也不能在100个吸烟的人中必有99人患有肺病,故(3)错误.故答案为(1).
【点睛】
本题主要考查了独立性检验的基本思想,是检验两个事件相关程度的量,是相关关系,是反映有关和无关的概率.
17.(1)答案见解析;(2);(3)13100元.
【分析】
(1)将已知数据代入相关系数的求解公式即可得解;
(2)根据题中数据及参考公式求得,,即可建立关于的线性回归方程;
(3)由题意知半年人均盈余为,得到不等式,解不等式即可.
【详解】
解:(1)由题意知,
因为与的相关系数近似为0.98,接近1,所以关于的线性相关程度非常高,因此可以用线性回归模型拟合与的关系.
(2),
,
所以.
(3)半年人均盈余为,
令,得,
故估计达到阶段小康标准的省(区、市)的半年人均可支配收入至少为13100元.
18.(1);(2)答案不唯一,见解析.
【分析】
(1)求出导函数,得切线斜率,从而可得切线方程;
(2)定义域是,在时直接由函数的解析式确定无零点(需用导数证明),在时,由导函数,得单调性,确定函数的最大值为,根据的正负分类讨论.在时,通过证明和,得零点个数.
【详解】
(1)当时,,,,,
所以曲线在处的切线方程为.
(2)函数的定义域为,.
①当时,,无零点.
②当时,,令,得,令,
得,所以在上单调递增,在上单调递减,所以有最大值.
当,即时,无零点.
当,即时,只有一个零点.
当,即时,,,
令,则,则在上单调递增,在上单调递减,
所以,所以,
因此当时,,.
因为,所以,于是.
又在上单调递增,,且,所以在上有唯一零点.
,
当时,,令,其中,则,
令,,则,
所以在上单调递增,,
所以在上单调递增,,
故当时,.因为,所以,即,
所以.
由,得,即,得,于是.
又,,在上单调递减,所以在上有唯一零点.故时,有两个零点.
③当时,由,得,则,又当时,,所以,无零点.
综上可知,或时,无零点;时,只有一个零点;时,有两个零点.
【点睛】
关键点点睛:本题考查导数的几何意义,考查用导数研究函数的零点个数.解题关键是求出函数的导数,由确定单调性和最值,本题在最大值的情况下,通过证明和,结合零点存在定理得出零点个数.难度较大,对学生的要求较高,属于困难题.
19.(1);(2).
【分析】
(1)利用导数直接求出函数的单调区间,即可求出的最小值
(2)若恒成立,则,即恒成立,令,利用导数研究函数单调性,进而得最值,可得实数a取值的范围即可
【详解】
(1)当时,,.
由得,由得,
所以在上单调递减,在上单调递增,
则函数的最小值为.
(2)由题得,若恒成立,则,即恒成立.
令,则,
当时,;当时,,
所以在上单调递减,在上单调递增,
则,所以,
故的取值范围为.
20.(1),表格答案见解析;(2)有99.5%的把握认为中学生使用手机对学习有影响.
【分析】
(1)由题意可得从而可求出的值,进而可填出列联表;
(2)直接利用公式求解,然后根据临界值表得结论
【详解】
解:(1)由己知得解得
补全表中所缺数据如下:
不使用手机 使用手机 合计
学习成绩优秀人数 28 12 40
学习成绩不优秀人数 14 26 40
合计 42 38 80
(2)根据题意计算观测值为,
所以有99.5%的把握认为中学生使用手机对学习有影响.
延边二中北校区(2020-2021)学年度上学期高二年级 期中考试 文科数学试卷
分卷I
一、单选题
1.函数在到之间的平均变化率为( )
A. B. C. D.
2.若(m为常数),则等于( )
A. B.1 C.m D.
3.在曲线上切线的倾斜角为的点的坐标为( )
A. B. C. D.或
4.若函数,则( )
A. B.1 C. D.3
5.下列求导结果正确的是( )
A. B.
C. D.
6.已知函数的导函数为,若的图象如图所示,则函数的图象可能是( )
A. B. C. D.
7.函数在处取得极值,则( )
A.,且为极大值点 B.,且为极小值点
C.,且为极大值点 D.,且为极小值点
8.设函数,则f(x)是( )
A.有一个零点的增函数 B.有一个零点的减函数
C.有二个零点的增函数 D.没有零点的减函数
9.已知两个变量,之间具有相关关系,现选用,,,四个模型得到相应的回归方程,并计算得到了相应的值分别为,,,,那么拟合效果最好的模型为
A. B. C. D.
10.在某次飞行航程中遭遇恶劣气候,55名男乘客中有24名晕机,34名女乘客中有8名晕机,在检验这些乘客晕机是否与性别有关时,采用的数据分析方法应是
A.频率分布直方图 B.回归分析 C.独立性检验 D.用样本估计总体
11.下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;②设有一个回归方程,变量x增加一个单位时,y平均增加5个单位;③线性回归直线必过;
④曲线上的点与该点的坐标之间具有相关关系;⑤在一个2×2列联表中,由计算得K2=13.079.则其两个变量间有关系的可能性是90%.其中错误的个数是
A.1 B.2 C.3 D.4
12.已知,对,且,恒有,则实数的取值范围是( )
A. B. C. D.
二、填空题
13.若有一组数据的总偏差平方和为100,相关指数=0.75,则其残差平方和为_______.
14.已知数据点(xi,yi)(i=1,2,3,…,n)在一条直线上,则相关系数r=________.
15.已知函数有三个零点,则实数的取值范围是__________.
16.在吸烟与患肺病是否相关的判断中,有下面的说法:
(1)从独立性分析可知在犯错误的概率不超过0.05的前提下,认为吸烟与患肺病有关系时,是指有的可能性使得推断错误.(2)从独立性分析可知在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系时,若某人吸烟,则他有的可能患有肺病;(3)若,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;其中说法正确的是________.
三、解答题
17.人均可支配收入是反映一个地区居民收入水平和城市经济发展水平的重要指标,并且对人均消费水平有重大影响,下图是根据国家统计局发布的《2020年上半年居民收入和消费支出情况》绘制的,是我国31个省(区、市)2020年上半年人均可支配收入(单位:元)与人均消费支出(单位:元)的散点图.
(1)由散点图可以看出,可以用线性回归模型拟合人均消费支出与人均可支配收入的关系,请用相关系数加以说明;
(2)建立关于的线性回归方程(精确到0.01);
(3)根据(2)的结论,规定半年人均盈余(人均可支配收入人均消费支出)不低于4620元的省(区、市)达到阶段小康的标准,则估计达到阶段小康标准的省(区、市)的半年人均可支配收入至少为多少元?
参考数据:
15500 9632 1412000000 683900000 38000 18400
参考公式:相关系数,
回归方程中斜率和截距的最小二乘估计公式分别为,.
18.已知函数,.
(1)当时,求曲线在处的切线方程;
(2)讨论函数的零点个数.
19.已知函数(为实数).
(1)若,求的最小值;
(2)若恒成立,求的取值范围.
20.随着手机的日益普及,学生使用手机对学校管理和学生发展带来诸多不利影响.为保护学生视力,让学生在学校专心学习,防止沉迷网络和游戏,促进学生身心健康发展,教育部于2021年1月15日下发文件《关于加强中小学生手机管理工作的通知》,对中小学生的手机使用和管理作出了相关的规定某研究型学习小组调查研究“中学生使用智能手机对学习的影响”,对我校80名学生调查得到部分统计数据如下表,记为事件:“学习成绩优秀且不使用手机”;为事件:“学习成绩不优秀且不使用手机”,且已知事件的频率是事件的频率的2倍.
不使用手机 使用手机 合计
学习成绩优秀人数
12
学习成绩不优秀人数
26
合计
(1)求表中,的值,并补全表中所缺数据;
(2)运用独立性检验思想,判断是否有99.5%的把握认为中学生使用手机对学习有影响?
参考数据:,其中.
0.10 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考答案
1.B
【分析】
直接代入平均变化率公式即得解.
【详解】
,
所以.
故选:B
【点睛】
本题主要考查平均变化率的计算,意在考查学生对该知识的理解掌握水平,属于基础题.
2.D
【分析】
根据导数的概念,直接计算,即可得出结果.
【详解】
由题意,根据导数的概念可得,
,
所以.
故选:D.
3.D
【分析】
利用导数的几何意义可求得结果.
【详解】
设所求点为,
因为,所以,因为切线的倾斜角为,所以切线斜率为,
即,所以,
则当时,;当时,,
所以所求点坐标为或.
故选:D
4.C
【分析】
求得导函数,代入即可求得结果.
【详解】
,则.
故选:C
5.C
【分析】
利用导数的求导法则以及复合函数的求导法则可判断各选项的正误.
【详解】
对于A选项,,A选项错误;
对于B选项,,B选项错误;
对于C选项,,C选项正确;
对于D选项,,D选项错误.
故选:C.
6.D
【分析】
根据导函数大于,原函数单调递增;导函数小于,原函数单调递减;即可得出正确答案.
【详解】
由导函数得图象可得:时,,所以在单调递减,
排除选项A、B,
当时,先正后负,所以在先增后减,
因选项C是先减后增再减,故排除选项C,
故选:D.
7.B
【分析】
先求导,再根据题意得,由此求得,再根据导数研究函数的极值.
【详解】
解:∵,
∴,
又在处取得极值,
∴,得,
∴,
由得,,即,
∴,即,
同理,由得,,
∴在处附近的左侧为负,右侧为正,
∴函数在处取得极小值,
故选:B.
【点睛】
本题主要考查利用函数的导数研究函数的单调性与极值,属于基础题.
8.A
【分析】
求导,由导数与单调性的关系判断增减性,利用零点存在定理判断零点所在区间,结合单调性即可判断零点个数.
【详解】
,则,
所以函数是定义域为上的连续的增函数,
又,,
零点存在定理可得在上存在唯一零点.
故选:.
【点睛】
本题考查了利用导数研究函数的单调性及函数零点的判定定理,属于基础题.
9.B
【详解】
越大,拟合效果越好,故选.
10.C
【详解】
根据题意,结合题目中的数据,列出2×2列联表,求出观测值K2,对照数表可得出概率结论,这种分析数据的方法是独立性检验.
本题选择C选项.
11.C
【详解】
对于①,方差反映一组数据的波动大小,将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变,故正确;对于②,一个回归方程,变量增加一个单位时,平均减小5个单位,故不正确;对于③,线性回归直线必过样本中心点,故正确;对于④,曲线上的点与该点的坐标之间具有一一对应关系,故不正确;对于⑤,有一个2×2列联表中,由计算得,则其两个变量间有关系的可能性是99.9%,故不正确.
故选C.
12.B
【分析】
依题意,得在上单调递增,转化为恒成立,则,令,利用的单调性可得答案.
【详解】
依题意,得,且,
,所以,
则在上单调递增,则,
恒成立,则,令,则,当时;当时,,
故,所以,
故选:B.
【点睛】
解题的关键点是含有参数的不等式恒成立的问题,可以进行参数分离,再构造函数,考查了学生分析问题、解决问题的能力.
13.25
【解析】
因为数据的总偏差平方和为,相关指数,,,故答案为.
14.±1
【分析】
由题意,数据点在一条直线上,可知相关系数的值,得到答案.
【详解】
由题易知,相关系数r=±1.
【点睛】
本题主要考查了相关性的应用,其中熟记相关系数的含义是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.
15.
【分析】
将问题转化为直线与函数的图象有三个交点,利用导数分析函数的单调性可求得的取值范围.
【详解】
构造,,有三个零点即与有三个交点,
,在和上单调递减,在上单调递增,
且,,即,
即,解得.
故答案为:.
【点睛】
本题考查利用函数的零点个数求参数,关键点是将问题转化为直线与函数的图象有三个交点,同时也考查了导数的应用,属于中等题.
16.(1)
【分析】
根据题意,利用独立性检验的定义与基本思想,对题目中的命题进行逐个分析、判断,即可求解出答案.
【详解】
根据独立性检验的基本思想,在犯错误的概率不超过0.05的前提下,认为吸烟与患肺病有关系的意思为有的把握认为这个推理是正确的,所以(1)正确.从独立性分析可知在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系的意思为有的把握认为这个推理是正确的,而不是说某个人吸烟就有的可能患有肺病,所以(2)错误.同(2)中的推论,所以也不能在100个吸烟的人中必有99人患有肺病,故(3)错误.故答案为(1).
【点睛】
本题主要考查了独立性检验的基本思想,是检验两个事件相关程度的量,是相关关系,是反映有关和无关的概率.
17.(1)答案见解析;(2);(3)13100元.
【分析】
(1)将已知数据代入相关系数的求解公式即可得解;
(2)根据题中数据及参考公式求得,,即可建立关于的线性回归方程;
(3)由题意知半年人均盈余为,得到不等式,解不等式即可.
【详解】
解:(1)由题意知,
因为与的相关系数近似为0.98,接近1,所以关于的线性相关程度非常高,因此可以用线性回归模型拟合与的关系.
(2),
,
所以.
(3)半年人均盈余为,
令,得,
故估计达到阶段小康标准的省(区、市)的半年人均可支配收入至少为13100元.
18.(1);(2)答案不唯一,见解析.
【分析】
(1)求出导函数,得切线斜率,从而可得切线方程;
(2)定义域是,在时直接由函数的解析式确定无零点(需用导数证明),在时,由导函数,得单调性,确定函数的最大值为,根据的正负分类讨论.在时,通过证明和,得零点个数.
【详解】
(1)当时,,,,,
所以曲线在处的切线方程为.
(2)函数的定义域为,.
①当时,,无零点.
②当时,,令,得,令,
得,所以在上单调递增,在上单调递减,所以有最大值.
当,即时,无零点.
当,即时,只有一个零点.
当,即时,,,
令,则,则在上单调递增,在上单调递减,
所以,所以,
因此当时,,.
因为,所以,于是.
又在上单调递增,,且,所以在上有唯一零点.
,
当时,,令,其中,则,
令,,则,
所以在上单调递增,,
所以在上单调递增,,
故当时,.因为,所以,即,
所以.
由,得,即,得,于是.
又,,在上单调递减,所以在上有唯一零点.故时,有两个零点.
③当时,由,得,则,又当时,,所以,无零点.
综上可知,或时,无零点;时,只有一个零点;时,有两个零点.
【点睛】
关键点点睛:本题考查导数的几何意义,考查用导数研究函数的零点个数.解题关键是求出函数的导数,由确定单调性和最值,本题在最大值的情况下,通过证明和,结合零点存在定理得出零点个数.难度较大,对学生的要求较高,属于困难题.
19.(1);(2).
【分析】
(1)利用导数直接求出函数的单调区间,即可求出的最小值
(2)若恒成立,则,即恒成立,令,利用导数研究函数单调性,进而得最值,可得实数a取值的范围即可
【详解】
(1)当时,,.
由得,由得,
所以在上单调递减,在上单调递增,
则函数的最小值为.
(2)由题得,若恒成立,则,即恒成立.
令,则,
当时,;当时,,
所以在上单调递减,在上单调递增,
则,所以,
故的取值范围为.
20.(1),表格答案见解析;(2)有99.5%的把握认为中学生使用手机对学习有影响.
【分析】
(1)由题意可得从而可求出的值,进而可填出列联表;
(2)直接利用公式求解,然后根据临界值表得结论
【详解】
解:(1)由己知得解得
补全表中所缺数据如下:
不使用手机 使用手机 合计
学习成绩优秀人数 28 12 40
学习成绩不优秀人数 14 26 40
合计 42 38 80
(2)根据题意计算观测值为,
所以有99.5%的把握认为中学生使用手机对学习有影响.
同课章节目录
