1.1—1.2有理数 复习课训练—2021-2022学年七年级数学人教版上册(Word版含答案)
文档属性
| 名称 | 1.1—1.2有理数 复习课训练—2021-2022学年七年级数学人教版上册(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 79.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 10:14:07 | ||
图片预览


文档简介
复习课一(1.1—1.2)
【例题选讲】
例1 如果全班某次数学成绩的平均成绩为83分,某同学考了85分,记作+2分,那么得90分记作__________分,-5分表示的是__________分.
例2 数轴上表示互为相反数的两个点A和B(点A在左),它们两点间的距离是5,则这两个数分别是__________和__________.若点C到点A的距离是3,则点C表示的数是__________或________.
例3 -3的相反数是( )
A.3 B.-3
C. D.-
例4 下列说法中:①-2是负分数;②1.5不是整数;③非负有理数不包括0;④整数和分数统称为有理数;⑤0是最小的有理数;⑥-1是最小的负整数.其中错误的有( )
A.1个 B.2个
C.3个 D.4个
归纳与整理:有理数的概念是初中阶段最基础的知识,无论在初中数学、高中数学以及其他学科的学习中都离不开它.
【相反数】只有符号不同的两个数,其中一个叫做另一个的相反数.零的相反数是零.
【绝对值】一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,零的绝对值为零.从数轴上看,一个数的绝对值是表示这个数的点离开原点的距离.
【大小比较】1.在数轴上表示的两个数,右边的数总比左边的数大.
2.正数都大于零,负数都小于零,正数大于负数.
3.两个正数比较大小,绝对值大的数大;两个负数比较大小,绝对值大的数反而小.
【课后练习】
1.下列各图中,表示数轴的是( )
2.有理数|-3|,-,-,+(-4),+|-5|中,负数的个数有( )
A.1个 B.2个 C.3个 D.4个
3.在数轴上表示-4的点离原点的距离等于( )
A.2 B.-2 C.±4 D.4
4.下列各语句中,错误的是( )
A.数轴上,原点位置的确定是任意的
B.数轴上,正方向可以是从原点向右,也可以是从原点向左
C.数轴上,单位长度1的长度的确定,可根据需要任意选取
D.数轴上,与原点的距离等于4的点有两个
5.一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动7个单位长度,这时点所对应的数是( )
A.3 B.1 C.-2 D.-4
6.如果a与5互为相反数,那么a等于( )
A.-5 B.5 C.- D.
7.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
8.若x为任意有理数,则-|-x|一定是( )
A.正数 B.负数
C.正数或零 D.负数或零
9.若生产成本降低10%记作-10%,则+8%表示________________.
10.有理数a,b在数轴上的位置如图,且|a|=2,|b|=3,则a=________,b=________.
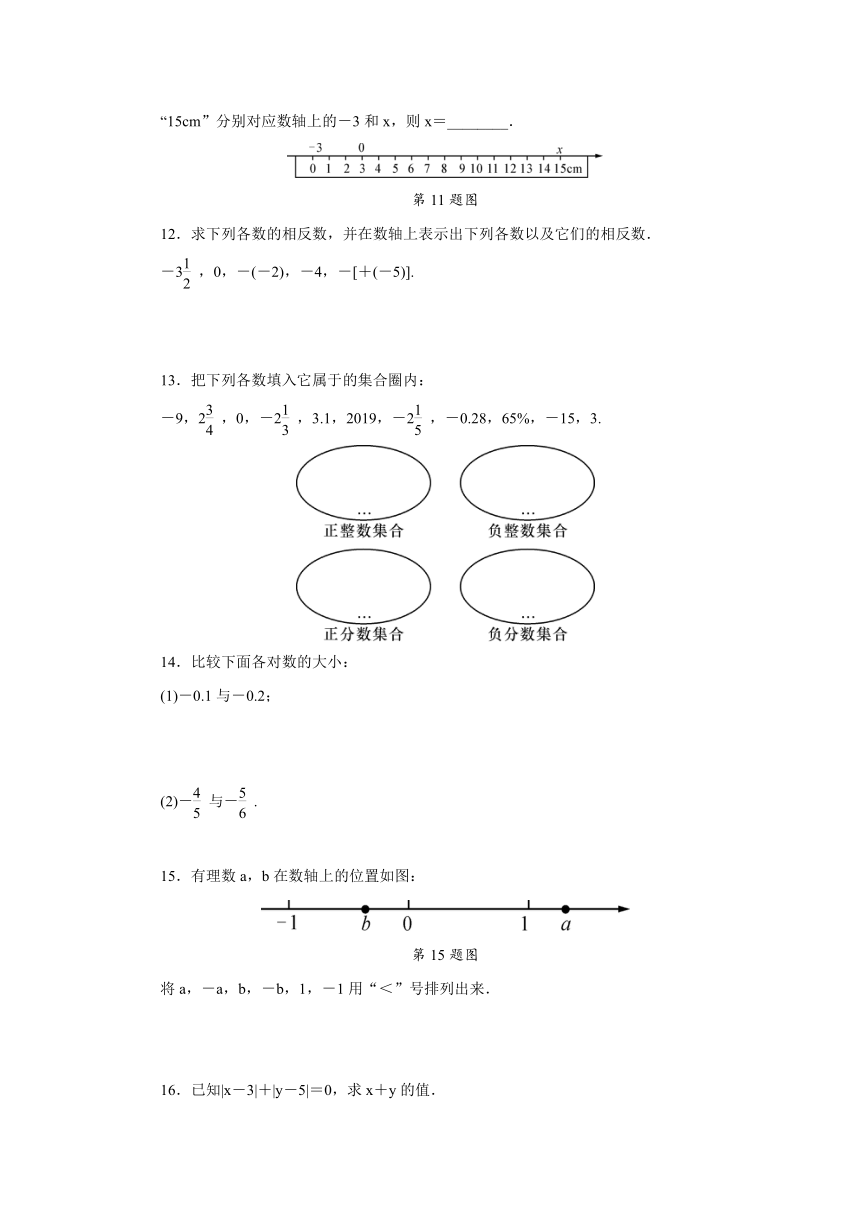
11.将一把刻度尺如图所示放在数轴上(数轴的单位长度是1cm),刻度尺上的“0cm”和“15cm”分别对应数轴上的-3和x,则x=________.
第11题图
12.求下列各数的相反数,并在数轴上表示出下列各数以及它们的相反数.
-3,0,-(-2),-4,-[+(-5)].
13.把下列各数填入它属于的集合圈内:
-9,2,0,-2,3.1,2019,-2,-0.28,65%,-15,3.
14.比较下面各对数的大小:
(1)-0.1与-0.2;
(2)-与-.
15.有理数a,b在数轴上的位置如图:
第15题图
将a,-a,b,-b,1,-1用“<”号排列出来.
16.已知|x-3|+|y-5|=0,求x+y的值.
17.小明到市行政中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作-1,小明从1楼出发,电梯上下楼情况依次记录如下:+5,-3,+11,-8,+12,-6,a;然后小明又回到了1楼.
(1)求a的值;
(2)该中心大楼每层楼高3m,电梯每向上或向下1m需要耗电0.1度,请你算算,小明办事时电梯需要耗电多少度(假定在此期间没有其他人乘坐电梯)?
18.阅读下列材料,我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离.即|x|=|x-0|,这个结论可以推广为|x1-x2|,表示在数轴上x1,x2对应点之间的距离.
例1:已知|x|=2,求x的值.
解:容易看出,在数轴上与原点距离为2的点对应的数为-2和2,即x的值为-2或2.
例2:已知|x-1|=2,求x的值.
解:在数轴上与数1对应的点距离为2的点对应的数为-1和3,即x的值为-1或3.
仿照阅读材料的解法,求下列各等式中x的值.
(1)|x|=3;
(2)|x-2|=4.
参考答案
【例题选讲】
例1 分析:把83分记作0,超过83分记为正数,不足83分记为负数.
+7 78
例2 分析:可以画出数轴,在点的两边确定相应距离.
-2.5 2.5 -5.5 0.5
例3 分析:可直接根据相反数的意义求解,方法一:数a的相反数是-a;方法二:在数轴上分居原点左右两侧且到原点的距离相等的两个数互为相反数.
A
例4 分析:小数是分数,非负有理数包括正有理数和零.
C
【课后练习】
1—5.DBDBD 6—8.ACD
9.生产成本提高8%
10.±2,3
11.12
12.相反数分别为:3,0,-2,4,-5.
在数轴上表示如图所示.
第12题图
13.
14.(1)因为|-0.1|=0.1,|-0.2|=0.2,且0.1<0.2,所以-0.1>-0.2.
(2)因为|-|==,|-|==,且<,所以->-.
15.由图看出:-a<-1<b<-b<1<a.
16.由|x-3|+|y-5|=0,得x-3=0,y-5=0.解得x=3,y=5.所以x+y=3+5=8.
17.(1)-11 (2)16.8度
18.(1)在数轴上与原点距离为3的点对应的数为-3和3.即x的值为-3或3.
(2)在数轴上与2对应的点的距离为4的点对应的数为6或-2.
【例题选讲】
例1 如果全班某次数学成绩的平均成绩为83分,某同学考了85分,记作+2分,那么得90分记作__________分,-5分表示的是__________分.
例2 数轴上表示互为相反数的两个点A和B(点A在左),它们两点间的距离是5,则这两个数分别是__________和__________.若点C到点A的距离是3,则点C表示的数是__________或________.
例3 -3的相反数是( )
A.3 B.-3
C. D.-
例4 下列说法中:①-2是负分数;②1.5不是整数;③非负有理数不包括0;④整数和分数统称为有理数;⑤0是最小的有理数;⑥-1是最小的负整数.其中错误的有( )
A.1个 B.2个
C.3个 D.4个
归纳与整理:有理数的概念是初中阶段最基础的知识,无论在初中数学、高中数学以及其他学科的学习中都离不开它.
【相反数】只有符号不同的两个数,其中一个叫做另一个的相反数.零的相反数是零.
【绝对值】一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,零的绝对值为零.从数轴上看,一个数的绝对值是表示这个数的点离开原点的距离.
【大小比较】1.在数轴上表示的两个数,右边的数总比左边的数大.
2.正数都大于零,负数都小于零,正数大于负数.
3.两个正数比较大小,绝对值大的数大;两个负数比较大小,绝对值大的数反而小.
【课后练习】
1.下列各图中,表示数轴的是( )
2.有理数|-3|,-,-,+(-4),+|-5|中,负数的个数有( )
A.1个 B.2个 C.3个 D.4个
3.在数轴上表示-4的点离原点的距离等于( )
A.2 B.-2 C.±4 D.4
4.下列各语句中,错误的是( )
A.数轴上,原点位置的确定是任意的
B.数轴上,正方向可以是从原点向右,也可以是从原点向左
C.数轴上,单位长度1的长度的确定,可根据需要任意选取
D.数轴上,与原点的距离等于4的点有两个
5.一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动7个单位长度,这时点所对应的数是( )
A.3 B.1 C.-2 D.-4
6.如果a与5互为相反数,那么a等于( )
A.-5 B.5 C.- D.
7.如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数.从轻重的角度看,最接近标准的是( )
8.若x为任意有理数,则-|-x|一定是( )
A.正数 B.负数
C.正数或零 D.负数或零
9.若生产成本降低10%记作-10%,则+8%表示________________.
10.有理数a,b在数轴上的位置如图,且|a|=2,|b|=3,则a=________,b=________.
11.将一把刻度尺如图所示放在数轴上(数轴的单位长度是1cm),刻度尺上的“0cm”和“15cm”分别对应数轴上的-3和x,则x=________.
第11题图
12.求下列各数的相反数,并在数轴上表示出下列各数以及它们的相反数.
-3,0,-(-2),-4,-[+(-5)].
13.把下列各数填入它属于的集合圈内:
-9,2,0,-2,3.1,2019,-2,-0.28,65%,-15,3.
14.比较下面各对数的大小:
(1)-0.1与-0.2;
(2)-与-.
15.有理数a,b在数轴上的位置如图:
第15题图
将a,-a,b,-b,1,-1用“<”号排列出来.
16.已知|x-3|+|y-5|=0,求x+y的值.
17.小明到市行政中心大楼办事,假定乘电梯向上一楼记作+1,向下一楼记作-1,小明从1楼出发,电梯上下楼情况依次记录如下:+5,-3,+11,-8,+12,-6,a;然后小明又回到了1楼.
(1)求a的值;
(2)该中心大楼每层楼高3m,电梯每向上或向下1m需要耗电0.1度,请你算算,小明办事时电梯需要耗电多少度(假定在此期间没有其他人乘坐电梯)?
18.阅读下列材料,我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离.即|x|=|x-0|,这个结论可以推广为|x1-x2|,表示在数轴上x1,x2对应点之间的距离.
例1:已知|x|=2,求x的值.
解:容易看出,在数轴上与原点距离为2的点对应的数为-2和2,即x的值为-2或2.
例2:已知|x-1|=2,求x的值.
解:在数轴上与数1对应的点距离为2的点对应的数为-1和3,即x的值为-1或3.
仿照阅读材料的解法,求下列各等式中x的值.
(1)|x|=3;
(2)|x-2|=4.
参考答案
【例题选讲】
例1 分析:把83分记作0,超过83分记为正数,不足83分记为负数.
+7 78
例2 分析:可以画出数轴,在点的两边确定相应距离.
-2.5 2.5 -5.5 0.5
例3 分析:可直接根据相反数的意义求解,方法一:数a的相反数是-a;方法二:在数轴上分居原点左右两侧且到原点的距离相等的两个数互为相反数.
A
例4 分析:小数是分数,非负有理数包括正有理数和零.
C
【课后练习】
1—5.DBDBD 6—8.ACD
9.生产成本提高8%
10.±2,3
11.12
12.相反数分别为:3,0,-2,4,-5.
在数轴上表示如图所示.
第12题图
13.
14.(1)因为|-0.1|=0.1,|-0.2|=0.2,且0.1<0.2,所以-0.1>-0.2.
(2)因为|-|==,|-|==,且<,所以->-.
15.由图看出:-a<-1<b<-b<1<a.
16.由|x-3|+|y-5|=0,得x-3=0,y-5=0.解得x=3,y=5.所以x+y=3+5=8.
17.(1)-11 (2)16.8度
18.(1)在数轴上与原点距离为3的点对应的数为-3和3.即x的值为-3或3.
(2)在数轴上与2对应的点的距离为4的点对应的数为6或-2.
