苏科版八年级数学下册第9章 中心对称图形——平行四边形 测试题(word版含答案)
文档属性
| 名称 | 苏科版八年级数学下册第9章 中心对称图形——平行四边形 测试题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 146.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 00:00:00 | ||
图片预览

文档简介
第9章
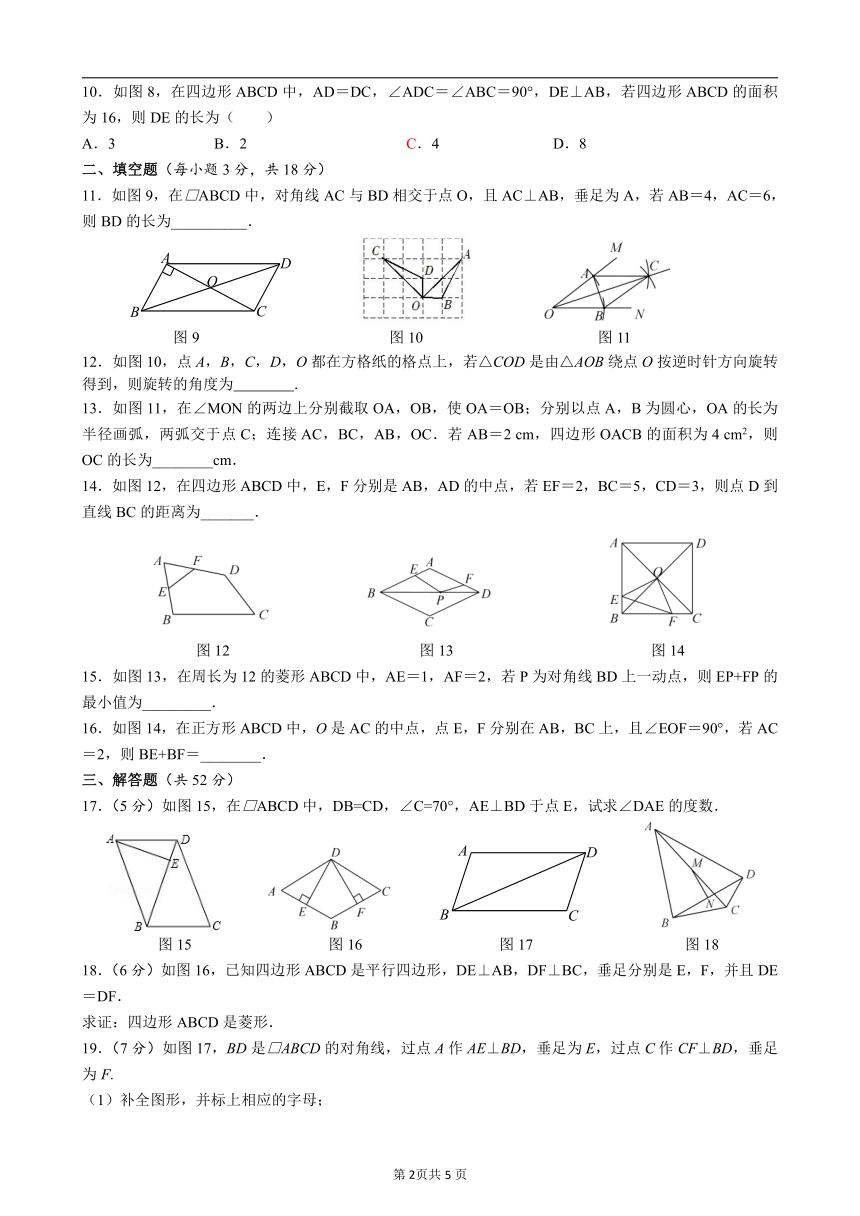
中心对称图形——平行四边形测试题
(本试卷满分100分)
选择题(每小题3分,共30分)
1.矩形、菱形、正方形都具有的性质是(
)
A.邻边相等
B.四个角都是直角
C.对角线相等
D.对角线互相平分
2.如图1,直线AB∥CD,P是AB上的动点,当点P的位置变化时,△PCD的面积将( )
A.变大
B.变小
C.不变
D.不确定
图1
图2
图3
图4
3.
下列图案是我国国产汽车品牌的标识,其中是中心对称图形的是(
)
A
B
C
D
4.如图2,在□ABCD中,∠ABC的平分线交AD于点E,∠BED=150°,则∠A的度数为(
)
A.150°
B.130°
C.120°
D.100°
5.如图3,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,分别取OA,OB的中点D,E,测出DE=12
m,那么A,B间的距离是(
)
A.24
m
B.20
m
C.30
m
D.18
m
6.如图4,过正方形ABCD的顶点B作直线l,过A,C作直线l的垂线,垂足分别为E,F,若AE=1,CF=3,则AB的长为(
)
A.
B.10
C.3
D.
7.如图5,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是(
)
A.6
B.12
C.24
D.48
图5
图6
图7
图8
8.如图6,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则添加下列条件能判定四边形ABCD为矩形的是(
)
A.AB=CD
B.OA=OC,OB=OD
C.AC⊥BD
D.AB∥CD,AD=BC
9.如图7,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10
B.12
C.18
D.24
10.如图8,在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD的面积为16,则DE的长为(
)
A.3
B.2
C.4
D.8
二、填空题(每小题3分,共18分)
11.如图9,在□ABCD中,对角线AC与BD相交于点O,且AC⊥AB,垂足为A,若AB=4,AC=6,则BD的长为__________.
(
A
B
C
D
A
O
)
图9
图10
图11
12.如图10,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转得到,则旋转的角度为
.
13.如图11,在∠MON的两边上分别截取OA,OB,使OA=OB;分别以点A,B为圆心,OA的长为半径画弧,两弧交于点C;连接AC,BC,AB,OC.若AB=2
cm,四边形OACB的面积为4
cm2,则OC的长为________cm.
14.如图12,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则点D到直线BC的距离为_______.
图12
图13
图14
15.如图13,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为_________.
16.如图14,在正方形ABCD中,O是AC的中点,点E,F分别在AB,BC上,且∠EOF=90°,若AC=2,则BE+BF=________.
三、解答题(共52分)
17.(5分)如图15,在□ABCD中,DB=CD,∠C=70°,AE⊥BD于点E,试求∠DAE的度数.
(
D
C
B
A
)
图15
图16
图17
图18
18.(6分)如图16,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E,F,并且DE=DF.
求证:四边形ABCD是菱形.
19.(7分)如图17,BD是□ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F.
(1)补全图形,并标上相应的字母;
(2)求证:AE=CF.
20.(8分)如图18,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点.
求证:(1)BM=DM;(2)MN⊥BD.
21.(8分)如图19,O为□ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E,F两点,求证AE=CF.
图19
图20
图21
22.(8分)如图20,在矩形ABCD中,DE平分∠ADC交AB于点E,连接CE,作EF⊥CE交AD于点F,连接CF,求∠BCE+∠DCF的度数.
23.(10分)如图21,在菱形ABCD中,AB=2,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与点B,C,D重合.
(1)求证:BE=CF;
(2)当点E,F在BC,CD上滑动时,四边形AECF的面积是否发生变化?如果不变,说明理由并求值.
附加题(20分,不计入总分)
24.某校数学兴趣小组开展了一次课外活动,过程如下:如图22-①,在正方形ABCD中,AB=4,将三角尺放在正方形ABCD上,使三角尺的直角顶点与D点重合.三角尺的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:AP=CQ;
(2)如图22-②,小明在图23-①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE与QE存在一定的数量关系,试猜测他的结论并予以证明;
(3)在(2)的条件下,若AP=1,求PE的长.
①
②
图22
第9章
中心对称图形——平行四边形测试题参考答案
一、1.D
2.C
3.B
4.C
5.A
6.A
7.C
8.B
9.B
10.C
二、11.10
12.90°
13.4
14.
15.3
16.
三、17.解:因为DB=CD,∠C=70°,所以∠DBC=∠C=70°.
又因为四边形ABCD是平行四边形,AD∥BC,所以∠ADB=∠DBC=70°.
又因为AE⊥BD,所以∠DAE=90°﹣∠ADB=90°﹣70°=20°.
18.证明:因为四边形ABCD是平行四边形,所以∠A=∠C.又因为DE⊥AB,DF⊥BC,所以∠AED=∠CFD=90°.又因为DE=DF,所以△ADE≌△CDF(AAS).所以AD=CD.所以□ABCD是菱形.
19.(1)解:依题意,可补全图形如图1所示.
(2)证明:因为AE⊥BD,CF⊥BD,所以∠AEB=∠CFD=90°.因为四边形ABCD是平行四边形,所以AB∥CD,AB=CD.所以∠ABE=∠CDF.所以△ABE≌△CDF.所以AE=CF.
图1
图2
图3
20.证明:(1)如图2所示,连接BM,DM.
因为∠ABC=∠ADC=90°,M是AC的中点,所以BM=AC,DM=AC.所以BM=DM.
(2)因为N是BD的中点,BM=DM,所以MN⊥BD.
21.
证明:因为四边形ABCD是平行四边形,所以AB∥CD,AB=CD.
所以∠OBE=∠ODF,∠E=∠F.
因为O为BC的中点,所以OB=OD.所以△EBO≌△FDO.所以BE=DF.所以BE-AB=DF-CD,即AE=CF.
22.
解:因为DE平分∠ADC,所以∠ADE=∠CDE.
因为四边形ABCD是矩形,所以AD=BC,∠A=∠B=∠BCD=90°,AB∥CD.
因为EF⊥CE,所以∠CEF=90°.所以∠AEF+∠BEC=90°.
因为∠AEF+∠AFE=90°,所以∠AFE=∠BEC.
因为AB∥CD,所以∠AED=∠CDE.所以∠ADE=∠AED.所以AD=AE.所以AE=BC.
所以△AEF≌△BCE.所以EF=CE.所以∠FCE=45°.所以∠BCE+∠DCF=45°.
23.(1)证明:因为四边形ABCD是菱形,∠BAD=120°,所以∠B=60°,∠BAC=∠BAD=60°.
所以△ABC为等边三角形,则AB=BC=AC.因为△AEF为等边三角形,所以AE=AF,∠EAF=60°.
所以∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF.所以△BAE≌△CAF.所以BE=CF.
(2)解:四边形AECF的面积不会发生变化.
理由:因为△BAE≌△CAF,所以S△ABE=S△ACF.所以S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC.
因为△ABC的面积是定值,所以四边形AECF的面积不会发生变化.
连接BD交AC于点O.在Rt△ABO中,AB=2,AO=1,由勾股定理,得BO=.
S△ABC=×2×=,即四边形AECF的面积是.
24.(1)证明:因为四边形ABCD是正方形,所以∠A=∠DCQ=90°,AD=CD,∠ADC=∠PDQ=90°.
所以∠ADP=∠CDQ.所以△ADP≌△CDQ(ASA).所以AP=CQ.
(2)解:PE=QE.
理由:因为△ADP≌△CDQ,所以PD=QD.因为DE平分∠PDQ,所以∠PDE=∠QDE.
在△PDE和△QDE中,PD=QD,∠PDE=∠QDE,DE=DE,所以△PDE≌△QDE(SAS).所以PE=QE.
(3)解:由(2),得PE=QE,由(1),得CQ=AP=1,所以BQ=BC+CQ=5,BP=AB-AP=3.
设PE=QE=x,则BE=5-x.
在Rt△BPE中,由勾股定理,得32+(5-x)2=x2,解得x=3.4,即PE的长为3.4.
第2页共5页
中心对称图形——平行四边形测试题
(本试卷满分100分)
选择题(每小题3分,共30分)
1.矩形、菱形、正方形都具有的性质是(
)
A.邻边相等
B.四个角都是直角
C.对角线相等
D.对角线互相平分
2.如图1,直线AB∥CD,P是AB上的动点,当点P的位置变化时,△PCD的面积将( )
A.变大
B.变小
C.不变
D.不确定
图1
图2
图3
图4
3.
下列图案是我国国产汽车品牌的标识,其中是中心对称图形的是(
)
A
B
C
D
4.如图2,在□ABCD中,∠ABC的平分线交AD于点E,∠BED=150°,则∠A的度数为(
)
A.150°
B.130°
C.120°
D.100°
5.如图3,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,分别取OA,OB的中点D,E,测出DE=12
m,那么A,B间的距离是(
)
A.24
m
B.20
m
C.30
m
D.18
m
6.如图4,过正方形ABCD的顶点B作直线l,过A,C作直线l的垂线,垂足分别为E,F,若AE=1,CF=3,则AB的长为(
)
A.
B.10
C.3
D.
7.如图5,菱形ABCD的周长是20,对角线AC,BD相交于点O,若BD=6,则菱形ABCD的面积是(
)
A.6
B.12
C.24
D.48
图5
图6
图7
图8
8.如图6,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则添加下列条件能判定四边形ABCD为矩形的是(
)
A.AB=CD
B.OA=OC,OB=OD
C.AC⊥BD
D.AB∥CD,AD=BC
9.如图7,矩形ABCD的对角线AC,BD相交于点O,CE∥BD,DE∥AC.若BD=6,则四边形CODE的周长是( )
A.10
B.12
C.18
D.24
10.如图8,在四边形ABCD中,AD=DC,∠ADC=∠ABC=90°,DE⊥AB,若四边形ABCD的面积为16,则DE的长为(
)
A.3
B.2
C.4
D.8
二、填空题(每小题3分,共18分)
11.如图9,在□ABCD中,对角线AC与BD相交于点O,且AC⊥AB,垂足为A,若AB=4,AC=6,则BD的长为__________.
(
A
B
C
D
A
O
)
图9
图10
图11
12.如图10,点A,B,C,D,O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转得到,则旋转的角度为
.
13.如图11,在∠MON的两边上分别截取OA,OB,使OA=OB;分别以点A,B为圆心,OA的长为半径画弧,两弧交于点C;连接AC,BC,AB,OC.若AB=2
cm,四边形OACB的面积为4
cm2,则OC的长为________cm.
14.如图12,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则点D到直线BC的距离为_______.
图12
图13
图14
15.如图13,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为_________.
16.如图14,在正方形ABCD中,O是AC的中点,点E,F分别在AB,BC上,且∠EOF=90°,若AC=2,则BE+BF=________.
三、解答题(共52分)
17.(5分)如图15,在□ABCD中,DB=CD,∠C=70°,AE⊥BD于点E,试求∠DAE的度数.
(
D
C
B
A
)
图15
图16
图17
图18
18.(6分)如图16,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E,F,并且DE=DF.
求证:四边形ABCD是菱形.
19.(7分)如图17,BD是□ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F.
(1)补全图形,并标上相应的字母;
(2)求证:AE=CF.
20.(8分)如图18,∠ABC=∠ADC=90°,M,N分别是AC,BD的中点.
求证:(1)BM=DM;(2)MN⊥BD.
21.(8分)如图19,O为□ABCD的对角线BD的中点,直线EF经过点O,分别交BA,DC的延长线于E,F两点,求证AE=CF.
图19
图20
图21
22.(8分)如图20,在矩形ABCD中,DE平分∠ADC交AB于点E,连接CE,作EF⊥CE交AD于点F,连接CF,求∠BCE+∠DCF的度数.
23.(10分)如图21,在菱形ABCD中,AB=2,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与点B,C,D重合.
(1)求证:BE=CF;
(2)当点E,F在BC,CD上滑动时,四边形AECF的面积是否发生变化?如果不变,说明理由并求值.
附加题(20分,不计入总分)
24.某校数学兴趣小组开展了一次课外活动,过程如下:如图22-①,在正方形ABCD中,AB=4,将三角尺放在正方形ABCD上,使三角尺的直角顶点与D点重合.三角尺的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:AP=CQ;
(2)如图22-②,小明在图23-①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE与QE存在一定的数量关系,试猜测他的结论并予以证明;
(3)在(2)的条件下,若AP=1,求PE的长.
①
②
图22
第9章
中心对称图形——平行四边形测试题参考答案
一、1.D
2.C
3.B
4.C
5.A
6.A
7.C
8.B
9.B
10.C
二、11.10
12.90°
13.4
14.
15.3
16.
三、17.解:因为DB=CD,∠C=70°,所以∠DBC=∠C=70°.
又因为四边形ABCD是平行四边形,AD∥BC,所以∠ADB=∠DBC=70°.
又因为AE⊥BD,所以∠DAE=90°﹣∠ADB=90°﹣70°=20°.
18.证明:因为四边形ABCD是平行四边形,所以∠A=∠C.又因为DE⊥AB,DF⊥BC,所以∠AED=∠CFD=90°.又因为DE=DF,所以△ADE≌△CDF(AAS).所以AD=CD.所以□ABCD是菱形.
19.(1)解:依题意,可补全图形如图1所示.
(2)证明:因为AE⊥BD,CF⊥BD,所以∠AEB=∠CFD=90°.因为四边形ABCD是平行四边形,所以AB∥CD,AB=CD.所以∠ABE=∠CDF.所以△ABE≌△CDF.所以AE=CF.
图1
图2
图3
20.证明:(1)如图2所示,连接BM,DM.
因为∠ABC=∠ADC=90°,M是AC的中点,所以BM=AC,DM=AC.所以BM=DM.
(2)因为N是BD的中点,BM=DM,所以MN⊥BD.
21.
证明:因为四边形ABCD是平行四边形,所以AB∥CD,AB=CD.
所以∠OBE=∠ODF,∠E=∠F.
因为O为BC的中点,所以OB=OD.所以△EBO≌△FDO.所以BE=DF.所以BE-AB=DF-CD,即AE=CF.
22.
解:因为DE平分∠ADC,所以∠ADE=∠CDE.
因为四边形ABCD是矩形,所以AD=BC,∠A=∠B=∠BCD=90°,AB∥CD.
因为EF⊥CE,所以∠CEF=90°.所以∠AEF+∠BEC=90°.
因为∠AEF+∠AFE=90°,所以∠AFE=∠BEC.
因为AB∥CD,所以∠AED=∠CDE.所以∠ADE=∠AED.所以AD=AE.所以AE=BC.
所以△AEF≌△BCE.所以EF=CE.所以∠FCE=45°.所以∠BCE+∠DCF=45°.
23.(1)证明:因为四边形ABCD是菱形,∠BAD=120°,所以∠B=60°,∠BAC=∠BAD=60°.
所以△ABC为等边三角形,则AB=BC=AC.因为△AEF为等边三角形,所以AE=AF,∠EAF=60°.
所以∠BAC-∠EAC=∠EAF-∠EAC,即∠BAE=∠CAF.所以△BAE≌△CAF.所以BE=CF.
(2)解:四边形AECF的面积不会发生变化.
理由:因为△BAE≌△CAF,所以S△ABE=S△ACF.所以S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC.
因为△ABC的面积是定值,所以四边形AECF的面积不会发生变化.
连接BD交AC于点O.在Rt△ABO中,AB=2,AO=1,由勾股定理,得BO=.
S△ABC=×2×=,即四边形AECF的面积是.
24.(1)证明:因为四边形ABCD是正方形,所以∠A=∠DCQ=90°,AD=CD,∠ADC=∠PDQ=90°.
所以∠ADP=∠CDQ.所以△ADP≌△CDQ(ASA).所以AP=CQ.
(2)解:PE=QE.
理由:因为△ADP≌△CDQ,所以PD=QD.因为DE平分∠PDQ,所以∠PDE=∠QDE.
在△PDE和△QDE中,PD=QD,∠PDE=∠QDE,DE=DE,所以△PDE≌△QDE(SAS).所以PE=QE.
(3)解:由(2),得PE=QE,由(1),得CQ=AP=1,所以BQ=BC+CQ=5,BP=AB-AP=3.
设PE=QE=x,则BE=5-x.
在Rt△BPE中,由勾股定理,得32+(5-x)2=x2,解得x=3.4,即PE的长为3.4.
第2页共5页
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
