六年级下册数学教案-7.1.13 正比例和反比例总复习苏教版
文档属性
| 名称 | 六年级下册数学教案-7.1.13 正比例和反比例总复习苏教版 |  | |
| 格式 | doc | ||
| 文件大小 | 508.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 13:45:37 | ||
图片预览

文档简介
正比例和反比例总复习
教学目标:
⑴使学生进一步认识成正比例和反比例的量,感受表示数量关系及其变化规律的不同数学模型;能运用比和比例的知识解决一些简单实际问题,丰富解决问题策略,积累解决问题的经验。
⑵让学生进一步体会比和比例知识的应用价值,感受不同领域的数学内容有着密切联系的。
⑶使学生在系统复习的过程中,体验与同学合作交流以及获取知识的乐趣,增进对数学学习的积极情感,增强学好数学的信心。
教学重点:进一步认识成正比例和反比例的量。
教学难点:感受比的应用价值,在活动中获得一些新的认识。
教学过程:
(一)回顾与交流一
1.多媒体出示表格:看到表格中的数量,你想到了什么?
数量(本) 1 2 3 4 5 6
总价(元) 5 10 15 20 25 30
引导学生说出:相关联的量,总价随着数量的变化而变化,但是比值不变,所以表中的两个数量成正比例。
继续出示:
速度(千米) 100 150 300 450 900
时间(小时) 9 6 3 2 1
引导学生说出:相关联的量,时间随着速度的变化而变化,但是乘积不变,所以表中的两个数量成反比例。
2.复习正比例和反比例的意义
对于正比例和反比例,你有哪些了解?
引导:那什么正比例的量,什么是成反比例的量呢?(意义理解)
3.相机复习正比例图像
出示 师指出:这表示一升柴油6元,逐步演示2升、3升、4升……的价钱。
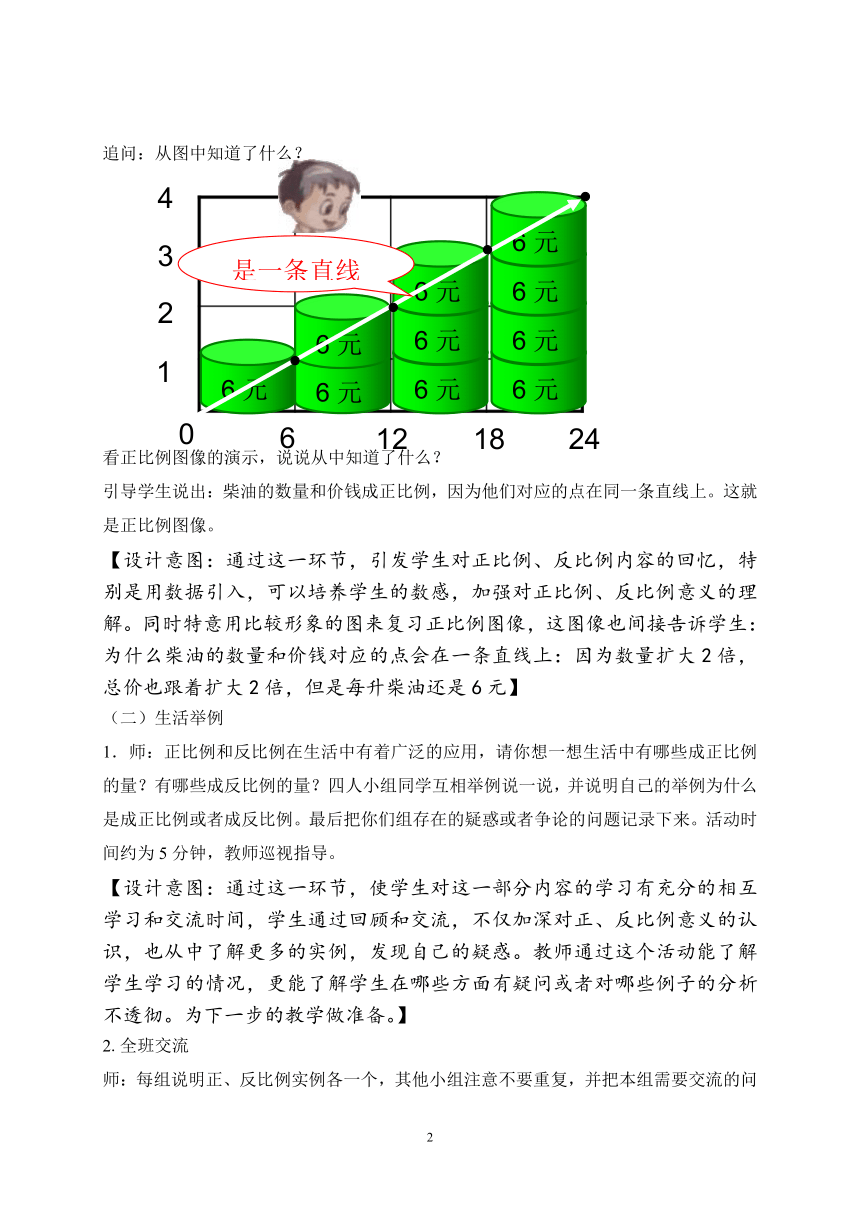
追问:从图中知道了什么?
看正比例图像的演示,说说从中知道了什么?
引导学生说出:柴油的数量和价钱成正比例,因为他们对应的点在同一条直线上。这就是正比例图像。
【设计意图:通过这一环节,引发学生对正比例、反比例内容的回忆,特别是用数据引入,可以培养学生的数感,加强对正比例、反比例意义的理解。同时特意用比较形象的图来复习正比例图像,这图像也间接告诉学生:为什么柴油的数量和价钱对应的点会在一条直线上:因为数量扩大2倍,总价也跟着扩大2倍,但是每升柴油还是6元】
(二)生活举例
1.师:正比例和反比例在生活中有着广泛的应用,请你想一想生活中有哪些成正比例的量?有哪些成反比例的量?四人小组同学互相举例说一说,并说明自己的举例为什么是成正比例或者成反比例。最后把你们组存在的疑惑或者争论的问题记录下来。活动时间约为5分钟,教师巡视指导。
【设计意图:通过这一环节,使学生对这一部分内容的学习有充分的相互学习和交流时间,学生通过回顾和交流,不仅加深对正、反比例意义的认识,也从中了解更多的实例,发现自己的疑惑。教师通过这个活动能了解学生学习的情况,更能了解学生在哪些方面有疑问或者对哪些例子的分析不透彻。为下一步的教学做准备。】
2.全班交流
师:每组说明正、反比例实例各一个,其他小组注意不要重复,并把本组需要交流的问题展示出来。其他小组判断说的是否正确。
3.比较一下正比例和反比例关系的相同点和不同点。完成表格。
师:说了那么多,那谁来总结一下正比例和反比例的联系和区别呢?
正比例 反比例
相同点 1、都有两种相关联的量。(两个变量)
2、都有一个定量。
不同点 1、变化方向相同。
2、相对应的两个数的比值一定。 1、变化方向相反。
2、相对应的两个数的乘积一定。
(三)应用练习
师:接下来,我们就来试试用我们对正反比例的理解来解决问题。
完成书上P84页第7题前3个表格的判断(独立完成,全班交流):判断每张表中的两种量是成正比例、反比例还是不成比例,并说明理由。
出示圆,说说,圆里有哪些相关的量,分别成什么比例?
引出:
对于圆的半径和面积不成比例,提供表格进行判断说明。
【设计意图:这个环节的设计是一个开放性的问题情境。出示圆,很快学生就找到:圆里相关的量有:半径、直径、周长、面积,这时,教师多媒体相机出示这些量,然后引导学生说直径和半径的比值、周长和直径的比值、周长和半径的比值都是一定的,所以它们都成正比例,而对于圆的半径和圆的面积,则借助表格,通过计算让学生更容易的理解到因为圆的面积和半径的乘积和比值都不一定,所以它们不成比例。】
完成P84页第8题,快速判断,说明理由。
师:在没有数据的情况下,你能判断吗两个数量成正比例、反比例还是不成比例,并说出理由吗?
(1)步测一段距离,每步的平均长度和走的步数。
(2)一台压路机滚筒滚动的转数和压路的面积
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间
(4)图书室的藏书量一定,每天借出和还回的本书
(5)已知xy=10,x和y
4.引出对等式中xy关系的判断。
师:有的时候,我们可以利用x和y之间的关系来直接判断它们是否成正比例和反比例呢?来试一试。出示下面的4个式子,小组内讨论交流每一个式子中的x和y成什么比例?
5.完成P85页第9题,独立完成,全班交流。
下面的图像表示一辆汽车在高速公路上行驶的路程与耗油量的关系。
(1)这辆汽车行驶的路程和耗油量成正比例吗?为什么?
(2)根据图像判断,行驶75千米大约耗油多少升?
下面的图像表示一辆汽车在高速公路上行驶的路程与耗油量的关系。
(2)如果汽车在市区行驶,每50千米耗油5升,照这样的耗油量,在上
图中描出行驶100千米、150千米……与耗油量对应点,再把它们按顺序连起来。
学生独立完成,多媒体反馈交流。
(四)拓展应用
师:同学们,其实,在生活中很多地方都要用到比例的知识来解决问题呢!
铺地实际问题。
出示:给一间教室铺地砖,如果地砖边长2分米,要用砖200块,如果改用边长2.5分米的地砖铺地,需要多少块?(请用比例的知识解答)
追问:地砖面积和砖的块数成什么比例?为什么?
引出:地砖的面积和用砖块数成反比例。
解:设需要x块。
2.5×2.5×x=2×2×200
6.25x=800
X=128
答:需要128块。
2、比例尺实际问题
在比例尺是1:6000000的地图上,量得两地距离是5厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米?
学生独立解决,说说怎么想的?(解答:略)
(五)学习总结
1.通过本节课的学习和交流,你有哪些收获?和你的同桌说一说。
2.关于正比例和反比例,你还有哪些问题?请会的同学帮助解答。
3.你还想了解有关正、反比例的哪些知识?老师可以给你们做一点简单的介绍。
【设计意图:整个教学设计本着开放:在开放的情境中使学生进一步认识成正比例和反比例的量,感受表示数量关系及其变化规律的不同数学模型;引导学生运用比和比例的知识解决问题,丰富解决问题策略,积累解决问题的经验。同时,有意识对教学内容进行了拓展和延伸,对课堂教学的密度也进行了强化,丰富学生的相关经验系统,让整个复习课更加丰满、立体】
6
教学目标:
⑴使学生进一步认识成正比例和反比例的量,感受表示数量关系及其变化规律的不同数学模型;能运用比和比例的知识解决一些简单实际问题,丰富解决问题策略,积累解决问题的经验。
⑵让学生进一步体会比和比例知识的应用价值,感受不同领域的数学内容有着密切联系的。
⑶使学生在系统复习的过程中,体验与同学合作交流以及获取知识的乐趣,增进对数学学习的积极情感,增强学好数学的信心。
教学重点:进一步认识成正比例和反比例的量。
教学难点:感受比的应用价值,在活动中获得一些新的认识。
教学过程:
(一)回顾与交流一
1.多媒体出示表格:看到表格中的数量,你想到了什么?
数量(本) 1 2 3 4 5 6
总价(元) 5 10 15 20 25 30
引导学生说出:相关联的量,总价随着数量的变化而变化,但是比值不变,所以表中的两个数量成正比例。
继续出示:
速度(千米) 100 150 300 450 900
时间(小时) 9 6 3 2 1
引导学生说出:相关联的量,时间随着速度的变化而变化,但是乘积不变,所以表中的两个数量成反比例。
2.复习正比例和反比例的意义
对于正比例和反比例,你有哪些了解?
引导:那什么正比例的量,什么是成反比例的量呢?(意义理解)
3.相机复习正比例图像
出示 师指出:这表示一升柴油6元,逐步演示2升、3升、4升……的价钱。
追问:从图中知道了什么?
看正比例图像的演示,说说从中知道了什么?
引导学生说出:柴油的数量和价钱成正比例,因为他们对应的点在同一条直线上。这就是正比例图像。
【设计意图:通过这一环节,引发学生对正比例、反比例内容的回忆,特别是用数据引入,可以培养学生的数感,加强对正比例、反比例意义的理解。同时特意用比较形象的图来复习正比例图像,这图像也间接告诉学生:为什么柴油的数量和价钱对应的点会在一条直线上:因为数量扩大2倍,总价也跟着扩大2倍,但是每升柴油还是6元】
(二)生活举例
1.师:正比例和反比例在生活中有着广泛的应用,请你想一想生活中有哪些成正比例的量?有哪些成反比例的量?四人小组同学互相举例说一说,并说明自己的举例为什么是成正比例或者成反比例。最后把你们组存在的疑惑或者争论的问题记录下来。活动时间约为5分钟,教师巡视指导。
【设计意图:通过这一环节,使学生对这一部分内容的学习有充分的相互学习和交流时间,学生通过回顾和交流,不仅加深对正、反比例意义的认识,也从中了解更多的实例,发现自己的疑惑。教师通过这个活动能了解学生学习的情况,更能了解学生在哪些方面有疑问或者对哪些例子的分析不透彻。为下一步的教学做准备。】
2.全班交流
师:每组说明正、反比例实例各一个,其他小组注意不要重复,并把本组需要交流的问题展示出来。其他小组判断说的是否正确。
3.比较一下正比例和反比例关系的相同点和不同点。完成表格。
师:说了那么多,那谁来总结一下正比例和反比例的联系和区别呢?
正比例 反比例
相同点 1、都有两种相关联的量。(两个变量)
2、都有一个定量。
不同点 1、变化方向相同。
2、相对应的两个数的比值一定。 1、变化方向相反。
2、相对应的两个数的乘积一定。
(三)应用练习
师:接下来,我们就来试试用我们对正反比例的理解来解决问题。
完成书上P84页第7题前3个表格的判断(独立完成,全班交流):判断每张表中的两种量是成正比例、反比例还是不成比例,并说明理由。
出示圆,说说,圆里有哪些相关的量,分别成什么比例?
引出:
对于圆的半径和面积不成比例,提供表格进行判断说明。
【设计意图:这个环节的设计是一个开放性的问题情境。出示圆,很快学生就找到:圆里相关的量有:半径、直径、周长、面积,这时,教师多媒体相机出示这些量,然后引导学生说直径和半径的比值、周长和直径的比值、周长和半径的比值都是一定的,所以它们都成正比例,而对于圆的半径和圆的面积,则借助表格,通过计算让学生更容易的理解到因为圆的面积和半径的乘积和比值都不一定,所以它们不成比例。】
完成P84页第8题,快速判断,说明理由。
师:在没有数据的情况下,你能判断吗两个数量成正比例、反比例还是不成比例,并说出理由吗?
(1)步测一段距离,每步的平均长度和走的步数。
(2)一台压路机滚筒滚动的转数和压路的面积
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间
(4)图书室的藏书量一定,每天借出和还回的本书
(5)已知xy=10,x和y
4.引出对等式中xy关系的判断。
师:有的时候,我们可以利用x和y之间的关系来直接判断它们是否成正比例和反比例呢?来试一试。出示下面的4个式子,小组内讨论交流每一个式子中的x和y成什么比例?
5.完成P85页第9题,独立完成,全班交流。
下面的图像表示一辆汽车在高速公路上行驶的路程与耗油量的关系。
(1)这辆汽车行驶的路程和耗油量成正比例吗?为什么?
(2)根据图像判断,行驶75千米大约耗油多少升?
下面的图像表示一辆汽车在高速公路上行驶的路程与耗油量的关系。
(2)如果汽车在市区行驶,每50千米耗油5升,照这样的耗油量,在上
图中描出行驶100千米、150千米……与耗油量对应点,再把它们按顺序连起来。
学生独立完成,多媒体反馈交流。
(四)拓展应用
师:同学们,其实,在生活中很多地方都要用到比例的知识来解决问题呢!
铺地实际问题。
出示:给一间教室铺地砖,如果地砖边长2分米,要用砖200块,如果改用边长2.5分米的地砖铺地,需要多少块?(请用比例的知识解答)
追问:地砖面积和砖的块数成什么比例?为什么?
引出:地砖的面积和用砖块数成反比例。
解:设需要x块。
2.5×2.5×x=2×2×200
6.25x=800
X=128
答:需要128块。
2、比例尺实际问题
在比例尺是1:6000000的地图上,量得两地距离是5厘米,甲乙两车同时从两地相向而行,3小时后两车相遇。已知甲乙两车的速度比是2:3,求甲乙两车的速度各是多少千米?
学生独立解决,说说怎么想的?(解答:略)
(五)学习总结
1.通过本节课的学习和交流,你有哪些收获?和你的同桌说一说。
2.关于正比例和反比例,你还有哪些问题?请会的同学帮助解答。
3.你还想了解有关正、反比例的哪些知识?老师可以给你们做一点简单的介绍。
【设计意图:整个教学设计本着开放:在开放的情境中使学生进一步认识成正比例和反比例的量,感受表示数量关系及其变化规律的不同数学模型;引导学生运用比和比例的知识解决问题,丰富解决问题策略,积累解决问题的经验。同时,有意识对教学内容进行了拓展和延伸,对课堂教学的密度也进行了强化,丰富学生的相关经验系统,让整个复习课更加丰满、立体】
6
