安徽省宿州市十三所重点中学2020-2021学年高二下学期期中质量检测理科数学试题 Word版含答案
文档属性
| 名称 | 安徽省宿州市十三所重点中学2020-2021学年高二下学期期中质量检测理科数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 762.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 16:54:31 | ||
图片预览



文档简介
1189990011620500宿州市十三所重点中学2020—2021学年度第二学期期中质量检测
高二数学(理科)试卷
(本试卷满分150分,考试时间120分钟)
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12个小题,每小题5分共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、若复数false的实部与虚部互为相反数,则false( )
A.false B.false C.false D.false
2、用反证法证明命题:“已知false、false是自然数,若false,则false、false中至少有一个不小于2”,提出的假设应该是( )
A.false、false中两个都不小于2
B.false、false中至少有一个小于2
C.false、false都小于2
D.false、false中至多有一个小于2
3、一木块沿某一斜面自由滑下,测得下滑的水平距离false与时间false之间的函数关系为false,则false时,此木块在水平方向的瞬时速度为( )
A.2 B.1 C.false D.false
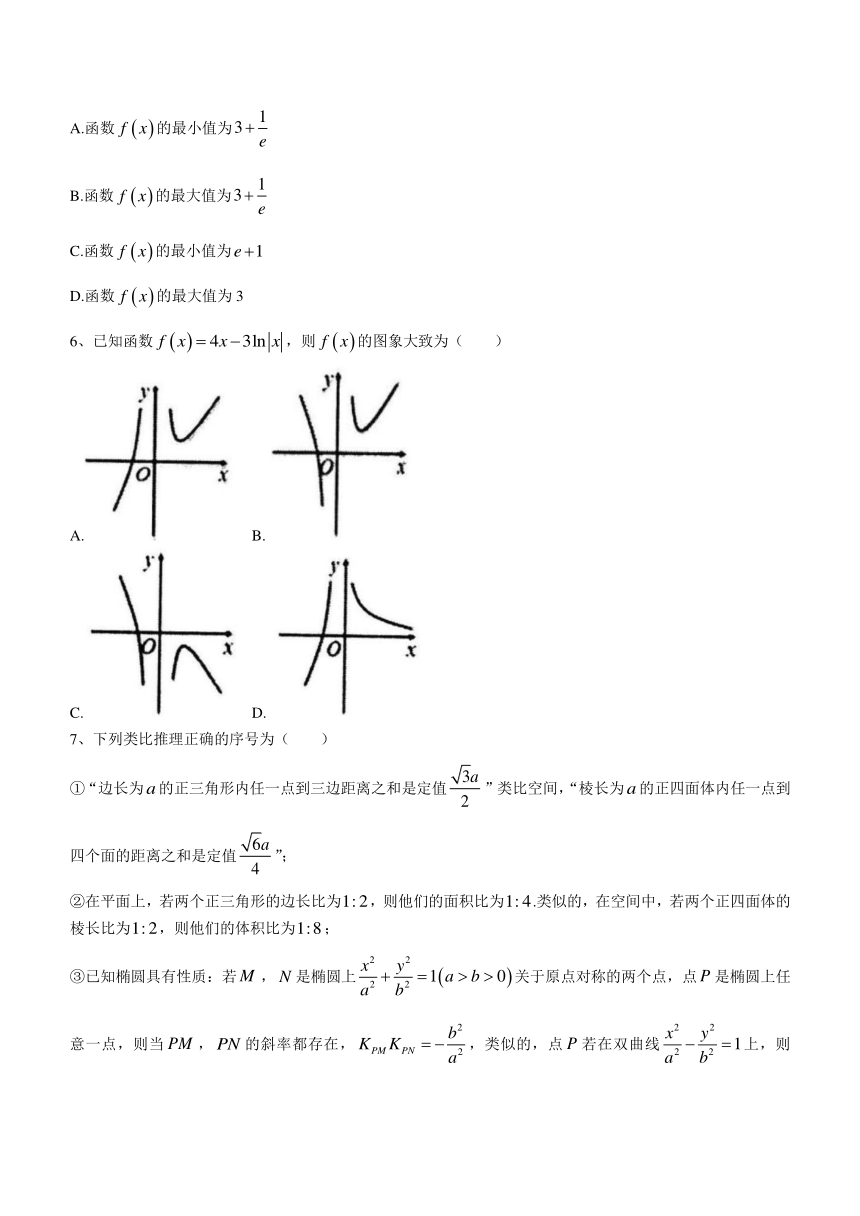
4、分形几何学是美籍法国数学家伯努瓦·B·曼德尔布罗特(Benoit.Mandelbrot)在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路.下图按照的分形规律生长成一个树形图,则第13行的实心圆点的个数是( )
A.55个 B.89个 C.144个 D.233个
5、已知函数false,false,则下列说法正确的是( )
A.函数false的最小值为false
B.函数false的最大值为false
C.函数false的最小值为false
D.函数false的最大值为3
6、已知函数false,则false的图象大致为( )
A. B.
C. D.
7、下列类比推理正确的序号为( )
①“边长为false的正三角形内任一点到三边距离之和是定值false”类比空间,“棱长为false的正四面体内任一点到四个面的距离之和是定值false”;
②在平面上,若两个正三角形的边长比为false,则他们的面积比为false.类似的,在空间中,若两个正四面体的棱长比为false,则他们的体积比为false;
③已知椭圆具有性质:若false,false是椭圆上false关于原点对称的两个点,点false是椭圆上任意一点,则当false,false的斜率都存在,false,类似的,点false若在双曲线false上,则false.
④长宽分别为false,false的矩形的外接圆的面积为false,类比空间中,长宽高分别为false,false,false的长方体的外接球的面积为false.
A.①③ B.②④ C.①④ D.②③
8、用数学归纳法证明不等式false时,从“false到false”左边需增加的代数式为( )
A.false B.false
C.false D.false
9、设正三棱柱的体积为false,当其表面积最小时,底面边长为( )
A.false B.false C.false D.false
10、若函数false恰有三个零点,则实数false的取值范围是( )
A.false B.false C.false D.false
11、设false为整数,对于任意的正整数false,false,则false的最小值是( )
A.2 B.3 C.4 D.5
12、设false是定义在false上的函数,其导函数为false,若false,false,则不等式false(其中false为自然对数的底数)的解集为( )
A.false B.false
C.false D.false
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分,把正确答案写在题中的横线上.
13、已知复数false满足false(false为虚数单位),则false的模为______.
14、已知false是曲线false上的任意一点,则false到直线false距离的最小值为______.
15、求值:false______.
16、已知函数false,若有且仅有一个整数false,使false,则实数false的取值范围是______.
三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17、(本小题满分10分)
已知false是自然对数的底数,函数false(false,且false).
(1)当false时,求函数false的单调区间;
(2)当false时,函数false的极大值为false,求false的值.
18、(本小题满分12分)
(1)已知false,证明:false.
(2)已知实数false,false,false,false满足false,用反证法证明:方程false与方程false至少有一个方程有实根.
19、(本小题满分12分)
设函数false,对任意实数false,false都有false
(1)求false的值;
(2)若false,求false,false,false的值;
(3)在(2)的条件下,猜想false的表达式,并用数学归纳法加以证明.
20、(本小题满分12分)
已知函数false.
(1)若false在定义域内单调递增,求实数false的范围;
(2)设函数false,若false至多有一个极值点,求false的取值集合.
21、(本小题满分12分)
如图,已知二次函数false,直线false,直线false(其中false,false为常数);若直线false与函数false的图象以及直线false,false与函数false的图象所围成的封闭图形如阴影所示.
(1)求阴影面积false关于false的函数false的解析式;
(2)若过点false,false可作曲线false,false的三条切线,求实数false的取值范围.
22、(本小题满分12分)
已知函数false.
(1)若函数false,讨论false的单调性;
(2)若函数false的导数false的两个零点从小到大依次为false,false,证明:false.
宿州市十三所重点中学2020—2021学年度第二学期期中质量检测
高二年级数学(理科)试卷参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
A
C
B
A
D
D
D
B
B
D
二、填空题
false 14、false 15、false 16、false
三、解答题
17、(1)函数的定义域为false.求导得false
当false时,令false,解得false或false,
函数false的单调递增区间为false,false;减区间为false.
(2)由(1)可知,当false时,函数false在区间false,false上单调递减,在false上单调递增,
于是当false时,函数false取到极大值,极大值为false,故false的值为false.
18.证明:(1)要证原不等式,只需证false.
∵false,∴两边均大于零.
因此只需证false,
只需证false,
只需证false,即证false
而false显然成立,∴原不等式成立.
(2)(反证法):
假设结论不成立,即方程false与方程false都没有实根,
则判别式满足false,false,
则false,
即false,即false,
即false,这与条件false矛盾,
即假设不成立,则原命题成立.
19.解:(Ⅰ)令false得:false
(Ⅱ)由false false
false
false
(Ⅲ)由(Ⅱ)猜想false
证明如下:(1)当false时,false,猜想成立
假设false时猜想成立,即false
则false
所以当false时,猜想也成立
综合(1)(2)可知,对一切false,都有false成立.
20、解:
(1)由题意得false,得false
令false,则false
由false得false
当false,false;false,false
故当false时,false
所以false.
(2)false,false
当false时,false,false;false,false,
所以0时false的唯一的极小值点。
当false时,令false得false,false
当false,false,false恒成立,false无极值。
故false的取值集合为false.
21、(1)由false得
false,∴false,false
∵false,∴直线false与false的图象的交点横坐标分别为false,false,
由定积分的几何意义知:
false
false
false,false
(2)∵曲线方程为false,false,∴false,
∴点false,false不在曲线上.设切点为false,则点false的坐标满足
false,因false,故切线的斜率为
false,整理得false.
∵过点false可作曲线的三条切线,
∴关于false方程false有三个实根.
设false,则false,由false得false
∵当false时,false∴false在false,false上单调递增,
∵当false时,false,∴false在false上单调递减.
∴函数false的极值点为false,
∴关于false方程false有三个实根的充要条件是false,
解得false,故所求的实数false的取值范围是false.
22、解:(1)∵false∴false.
当false时,false,false
∴false在false上单调递增,在false上单调递减;
当false时,false或false,false
∴false在false,false上单调递增,在false上单调递减;
当false时,false或false,false
∴false在false,false上单调递增,在false上单调递减;
当false时,false在false上恒成立,
所以false在false上单调递增;
(2)∵false.
且false的两个零点从小到大依次为false,false
∴false,false是方程false的两个根,
∴false
又false,false且false所以false
欲证false,即证false
只需证false
令false,false
∴false在false上单调递增,false上单调递减,
∴false,即false成立.
高二数学(理科)试卷
(本试卷满分150分,考试时间120分钟)
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12个小题,每小题5分共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、若复数false的实部与虚部互为相反数,则false( )
A.false B.false C.false D.false
2、用反证法证明命题:“已知false、false是自然数,若false,则false、false中至少有一个不小于2”,提出的假设应该是( )
A.false、false中两个都不小于2
B.false、false中至少有一个小于2
C.false、false都小于2
D.false、false中至多有一个小于2
3、一木块沿某一斜面自由滑下,测得下滑的水平距离false与时间false之间的函数关系为false,则false时,此木块在水平方向的瞬时速度为( )
A.2 B.1 C.false D.false
4、分形几何学是美籍法国数学家伯努瓦·B·曼德尔布罗特(Benoit.Mandelbrot)在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路.下图按照的分形规律生长成一个树形图,则第13行的实心圆点的个数是( )
A.55个 B.89个 C.144个 D.233个
5、已知函数false,false,则下列说法正确的是( )
A.函数false的最小值为false
B.函数false的最大值为false
C.函数false的最小值为false
D.函数false的最大值为3
6、已知函数false,则false的图象大致为( )
A. B.
C. D.
7、下列类比推理正确的序号为( )
①“边长为false的正三角形内任一点到三边距离之和是定值false”类比空间,“棱长为false的正四面体内任一点到四个面的距离之和是定值false”;
②在平面上,若两个正三角形的边长比为false,则他们的面积比为false.类似的,在空间中,若两个正四面体的棱长比为false,则他们的体积比为false;
③已知椭圆具有性质:若false,false是椭圆上false关于原点对称的两个点,点false是椭圆上任意一点,则当false,false的斜率都存在,false,类似的,点false若在双曲线false上,则false.
④长宽分别为false,false的矩形的外接圆的面积为false,类比空间中,长宽高分别为false,false,false的长方体的外接球的面积为false.
A.①③ B.②④ C.①④ D.②③
8、用数学归纳法证明不等式false时,从“false到false”左边需增加的代数式为( )
A.false B.false
C.false D.false
9、设正三棱柱的体积为false,当其表面积最小时,底面边长为( )
A.false B.false C.false D.false
10、若函数false恰有三个零点,则实数false的取值范围是( )
A.false B.false C.false D.false
11、设false为整数,对于任意的正整数false,false,则false的最小值是( )
A.2 B.3 C.4 D.5
12、设false是定义在false上的函数,其导函数为false,若false,false,则不等式false(其中false为自然对数的底数)的解集为( )
A.false B.false
C.false D.false
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分,把正确答案写在题中的横线上.
13、已知复数false满足false(false为虚数单位),则false的模为______.
14、已知false是曲线false上的任意一点,则false到直线false距离的最小值为______.
15、求值:false______.
16、已知函数false,若有且仅有一个整数false,使false,则实数false的取值范围是______.
三、解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17、(本小题满分10分)
已知false是自然对数的底数,函数false(false,且false).
(1)当false时,求函数false的单调区间;
(2)当false时,函数false的极大值为false,求false的值.
18、(本小题满分12分)
(1)已知false,证明:false.
(2)已知实数false,false,false,false满足false,用反证法证明:方程false与方程false至少有一个方程有实根.
19、(本小题满分12分)
设函数false,对任意实数false,false都有false
(1)求false的值;
(2)若false,求false,false,false的值;
(3)在(2)的条件下,猜想false的表达式,并用数学归纳法加以证明.
20、(本小题满分12分)
已知函数false.
(1)若false在定义域内单调递增,求实数false的范围;
(2)设函数false,若false至多有一个极值点,求false的取值集合.
21、(本小题满分12分)
如图,已知二次函数false,直线false,直线false(其中false,false为常数);若直线false与函数false的图象以及直线false,false与函数false的图象所围成的封闭图形如阴影所示.
(1)求阴影面积false关于false的函数false的解析式;
(2)若过点false,false可作曲线false,false的三条切线,求实数false的取值范围.
22、(本小题满分12分)
已知函数false.
(1)若函数false,讨论false的单调性;
(2)若函数false的导数false的两个零点从小到大依次为false,false,证明:false.
宿州市十三所重点中学2020—2021学年度第二学期期中质量检测
高二年级数学(理科)试卷参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
A
C
B
A
D
D
D
B
B
D
二、填空题
false 14、false 15、false 16、false
三、解答题
17、(1)函数的定义域为false.求导得false
当false时,令false,解得false或false,
函数false的单调递增区间为false,false;减区间为false.
(2)由(1)可知,当false时,函数false在区间false,false上单调递减,在false上单调递增,
于是当false时,函数false取到极大值,极大值为false,故false的值为false.
18.证明:(1)要证原不等式,只需证false.
∵false,∴两边均大于零.
因此只需证false,
只需证false,
只需证false,即证false
而false显然成立,∴原不等式成立.
(2)(反证法):
假设结论不成立,即方程false与方程false都没有实根,
则判别式满足false,false,
则false,
即false,即false,
即false,这与条件false矛盾,
即假设不成立,则原命题成立.
19.解:(Ⅰ)令false得:false
(Ⅱ)由false false
false
false
(Ⅲ)由(Ⅱ)猜想false
证明如下:(1)当false时,false,猜想成立
假设false时猜想成立,即false
则false
所以当false时,猜想也成立
综合(1)(2)可知,对一切false,都有false成立.
20、解:
(1)由题意得false,得false
令false,则false
由false得false
当false,false;false,false
故当false时,false
所以false.
(2)false,false
当false时,false,false;false,false,
所以0时false的唯一的极小值点。
当false时,令false得false,false
当false,false,false恒成立,false无极值。
故false的取值集合为false.
21、(1)由false得
false,∴false,false
∵false,∴直线false与false的图象的交点横坐标分别为false,false,
由定积分的几何意义知:
false
false
false,false
(2)∵曲线方程为false,false,∴false,
∴点false,false不在曲线上.设切点为false,则点false的坐标满足
false,因false,故切线的斜率为
false,整理得false.
∵过点false可作曲线的三条切线,
∴关于false方程false有三个实根.
设false,则false,由false得false
∵当false时,false∴false在false,false上单调递增,
∵当false时,false,∴false在false上单调递减.
∴函数false的极值点为false,
∴关于false方程false有三个实根的充要条件是false,
解得false,故所求的实数false的取值范围是false.
22、解:(1)∵false∴false.
当false时,false,false
∴false在false上单调递增,在false上单调递减;
当false时,false或false,false
∴false在false,false上单调递增,在false上单调递减;
当false时,false或false,false
∴false在false,false上单调递增,在false上单调递减;
当false时,false在false上恒成立,
所以false在false上单调递增;
(2)∵false.
且false的两个零点从小到大依次为false,false
∴false,false是方程false的两个根,
∴false
又false,false且false所以false
欲证false,即证false
只需证false
令false,false
∴false在false上单调递增,false上单调递减,
∴false,即false成立.
同课章节目录
