2020-2021学年七年级数学苏科版下册第7章 平面图形的认识(二)期末复习提升训练(word版含解析)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册第7章 平面图形的认识(二)期末复习提升训练(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 415.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 10:56:18 | ||
图片预览

文档简介
平面图形的认识(二)(1)
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、如图,下列说法中错误的是( )
A.∠3和∠5是同位角 B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角 D.∠2和∠5是内错角
2、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
3、如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )
A.28° B.22° C.32° D.38°
4、如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm B.18cm C.19cm D.20cm
5、用一根长为10cm的绳子围成一个三角形,若所围成的三角形中一边的长为2cm,且另外两边长的值均为整数,则这样的围法有( )
A.1种 B.2种 C.3种 D.4种
6、如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
7、如图,直线AE∥DF,若∠ABC=120°,∠DCB=95°,则∠1+∠2的度数为( )
A.45° B.55° C.35° D.不能确定
8、小明把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于( )
A.120° B.150° C.180° D.210°
9、马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830°,则该多边形的边数是( )
A.7 B.8 C.7或8 D.无法确定
10、如图,平面内直线a∥b∥c,点A,B,C分别在直线a,b,c上,BD平分∠ABC,并且满足∠α>∠β,则∠α,∠β,∠γ关系正确的是( )
A.∠α=∠β+2∠γ B.∠α=∠β+∠γ C.∠α=2∠β﹣2∠γ D.∠α=2∠β﹣∠γ
二、填空题
11、如图,与是同位角的是__________.
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段,.则我们可以判定的依据是__________.
13、如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为_________.
14、如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_____.
15、一个等腰三角形的两边长分别为4cm和9cm,则它的周长为__cm.
16、如图,AB∥CD,则∠1+∠3—∠2的度数等于 __________.
17、若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.
18、小林从P点向西直走12米后向左转,转动的角度为α,再直走12米,又向左转α,如此重复,小林共走了108米后回到点P,则α=____.
19、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG的度数 度,再沿BF折叠成图c.则图中的∠CFE的度数是 度.
20、如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ,则∠A2= ,∠An= .
三、解答题
21、如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
22、如图,已知:∠ABE+∠DEB=180°,∠1=∠2,则∠F与∠G的大小关系如何?请说明理由
23、如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC向左平移5个单位得到△DEF.
(1)在正方形网格中,作出△DEF;
(2)设网格小正方形的边长为1,求平移过程中线段AC所扫过的图形面积.
24、如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB.
(Ⅰ)若∠A=60°,则∠BOC的度数为 ;
(Ⅱ)若∠A=100°,则∠BOC的度数 ;
(Ⅲ)若∠A=α,求∠BOC的度数,并说明理由.
25、如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
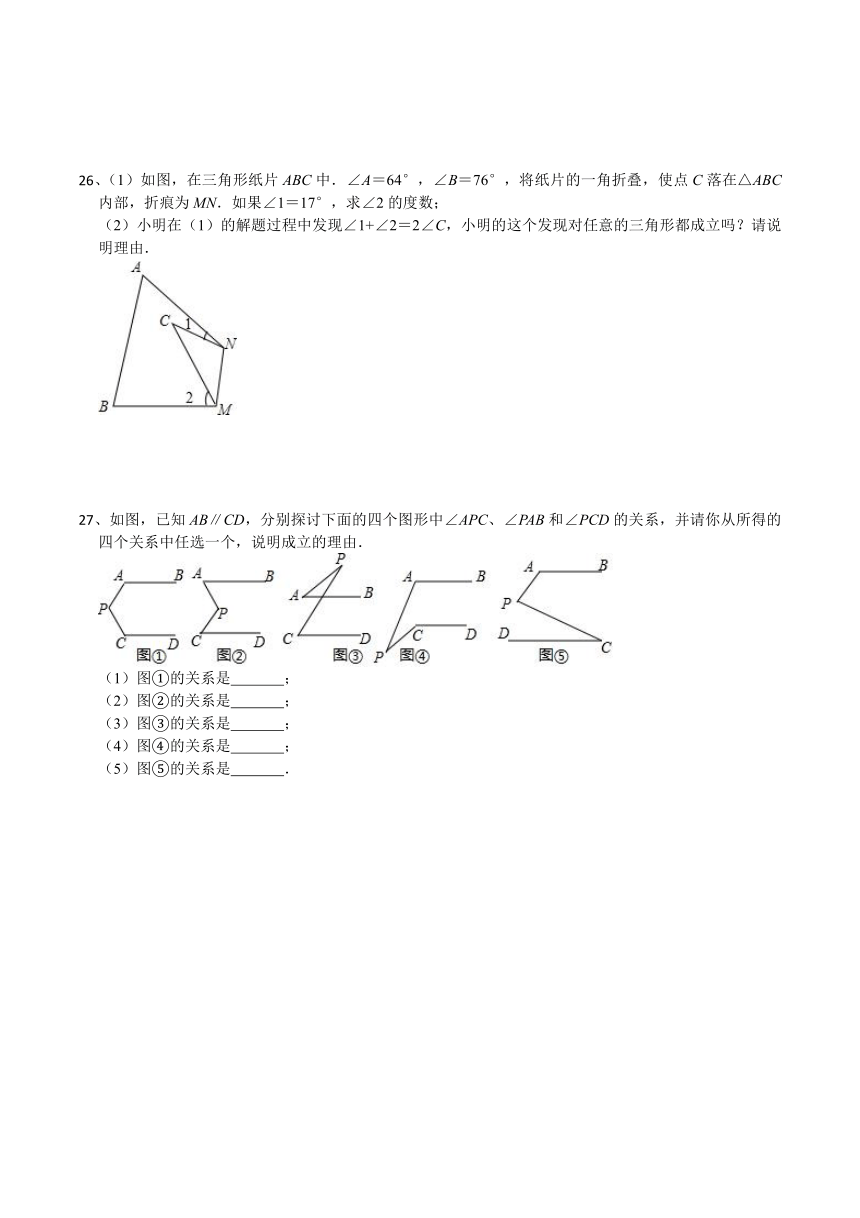
26、(1)如图,在三角形纸片ABC中.∠A=64°,∠B=76°,将纸片的一角折叠,使点C落在△ABC内部,折痕为MN.如果∠1=17°,求∠2的度数;
(2)小明在(1)的解题过程中发现∠1+∠2=2∠C,小明的这个发现对任意的三角形都成立吗?请说明理由.
27、如图,已知AB∥CD,分别探讨下面的四个图形中∠APC、∠PAB和∠PCD的关系,并请你从所得的四个关系中任选一个,说明成立的理由.
(1)图①的关系是 ;
(2)图②的关系是 ;
(3)图③的关系是 ;
(4)图④的关系是 ;
(5)图⑤的关系是 .
平面图形的认识(二)(1)(解析)
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、如图,下列说法中错误的是( )
A.∠3和∠5是同位角 B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角 D.∠2和∠5是内错角
【分析】根据同位角,同旁内角,对顶角以及内错角的定义进行判断.
【答案】解:A、∠3和∠5是同位角,故本选项不符合题意.
B、∠4和∠5是同旁内角,故本选项不符合题意.
C、∠2和∠4是对顶角,故本选项不符合题意.
D、∠2和∠5不是内错角,故本选项符合题意.
故选:D.
2、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
【答案】解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
3、如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )
A.28° B.22° C.32° D.38°
【分析】延长AB交CF于E,求出∠ABC,根据三角形外角性质求出∠AEC,根据平行线性质得出∠2=∠AEC,代入求出即可.
【答案】解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵∠1=38°,
∴∠AEC=∠ABC﹣∠1=22°,
∵GH∥EF,
∴∠2=∠AEC=22°,
故选:B.
4、如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm B.18cm C.19cm D.20cm
【分析】根据平移的定义求得AA'和BC'的长,则四边形的周长即可求解.
【答案】解:由题意知,BB'=CC'=AA'=3cm,
则四边形ABC'A'的周长=12+3+3=18cm.
故选:B.
5、用一根长为10cm的绳子围成一个三角形,若所围成的三角形中一边的长为2cm,且另外两边长的值均为整数,则这样的围法有( )
A.1种 B.2种 C.3种 D.4种
【分析】根据三角形的两边之和大于第三边,根据周长是10厘米,可知最长的边要小于5厘米,进而得出三条边的情况.
【答案】解:∵三角形中一边的长为2cm,且另外两边长的值均为整数,
∴三条边分别是2cm、4cm、4cm.
故选:A.
6、如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
【分析】依据平行线的性质,即可得到∠1=∠DFG=40°,再根据三角形外角性质,即可得到∠2的度数.
【答案】解:∵DF∥EG,
∴∠1=∠DFG=40°,
又∵∠A=30°,
∴∠2=∠A+∠DFG=30°+40°=70°,
故选:D.
7、如图,直线AE∥DF,若∠ABC=120°,∠DCB=95°,则∠1+∠2的度数为( )
A.45° B.55° C.35° D.不能确定
【分析】利用平行线的性质以及三角形的外角的性质解决问题即可.
【答案】解:∵AE∥DF,
∴∠3+∠4=180°,
∵∠ABC=∠1+∠3=120°,∠DCB=∠2+∠4=95°,
∴∠1+∠3+∠2+∠4=120°+95°,
∴∠1+∠2=215°﹣180°=35°,
故选:C.
8、小明把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于( )
A.120° B.150° C.180° D.210°
【分析】根据三角形的内角和定理和三角形外角性质解答即可.
【答案】解:如图:
∵∠1=∠D+∠DOA,∠2=∠E+∠EPB,
∵∠DOA=∠COP,∠EPB=∠CPO,
∴∠1+∠2=∠D+∠E+∠COP+∠CPO=∠D+∠E+180°﹣∠C=30°+90°+180°﹣90°=210°,
故选:D.
9、马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830°,则该多边形的边数是( )
A.7 B.8 C.7或8 D.无法确定
【分析】n边形的内角和是(n﹣2)?180°,即为180°的(n﹣2)倍,多边形的内角一定大于0度,小于180度,因而多边形中,除去2个内角外,其余内角和与180度的商加上2,以后所得的数值,比这个数值大1或2的整数就是多边形的边数.
【答案】解:设少加的2个内角和为x度,边数为n.
则(n﹣2)×180=830+x,
即(n﹣2)×180=4×180+110+x,
因此x=70,n=7或x=250,n=8.
故该多边形的边数是7或8.
故选:C.
10、如图,平面内直线a∥b∥c,点A,B,C分别在直线a,b,c上,BD平分∠ABC,并且满足∠α>∠β,则∠α,∠β,∠γ关系正确的是( )
A.∠α=∠β+2∠γ B.∠α=∠β+∠γ C.∠α=2∠β﹣2∠γ D.∠α=2∠β﹣∠γ
【分析】根据平行线的性质和角平分线的性质,可以得到∠α,∠β,∠γ的关系,本题得以解决.
【解答】解:∵直线a∥b∥c,
∴∠α=∠ABD+∠γ,∠β=∠CBD﹣∠γ,
∴∠ABD=∠α﹣∠γ,∠CBD=∠β+∠γ,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠α﹣∠γ=∠β+∠γ,
∴∠α=∠β+2∠γ,
故选:A.
二、填空题
11、如图,与是同位角的是__________.
【答案】①②
【提示】
根据同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【详解】
解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②.
故答案为:①②.
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段,.则我们可以判定的依据是__________.
【答案】内错角相等,两直线平行
【提示】
直接根据内错角相等,两直线平行即可解答.
【详解】
∵∠ADC=∠BAD=30°,
∴AB//CD(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
13、如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为_________.
【答案】55°
【解析】
试题提示:先根据邻补角的性质求得∠ADF的度数,再根据平行线的性质求解即可.
∵∠ADE=125°
∴∠ADF=55°
∵AD∥BC
∴∠DBC=∠ADF=55°.
14、如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_____.
【答案】20cm.
【提示】
根据平移的性质可得DF=AE,然后判断出四边形ABFD的周长=△ABE的周长+AD+EF,然后代入数据计算即可得解.
【详解】
解:∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴四边形ABFD的周长=AB+BE+DF+AD+EF,
=AB+BE+AE+AD+EF,
=16+AD+EF,
∵平移距离为2cm,
∴AD=EF=2cm,
∴四边形ABFD的周长=16+2+2=20cm.
故答案为20cm.
15、一个等腰三角形的两边长分别为4cm和9cm,则它的周长为__cm.
【答案】22
【提示】
底边可能是4,也可能是9,分类讨论,去掉不合条件的,然后可求周长.
【详解】
试题解析:①当腰是4cm,底边是9cm时:不满足三角形的三边关系,因此舍去.
②当底边是4cm,腰长是9cm时,能构成三角形,则其周长=4+9+9=22cm.
故填22.
16、如图,AB∥CD,则∠1+∠3—∠2的度数等于 __________.
【答案】180°
【详解】解:∵AB∥CD∴∠1=∠EFD
∵∠2+∠EFC=∠3, ∠EFD=180°-∠EFC, ∴∠1+∠3—∠2=180°
故答案为:180°
17、若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.
【答案】8
【详解】
解:设边数为n,由题意得,
180(n-2)=3603
解得n=8.
所以这个多边形的边数是8.
18、小林从P点向西直走12米后向左转,转动的角度为α,再直走12米,又向左转α,如此重复,小林共走了108米后回到点P,则α=____.
【答案】40°
【解析】
∵108÷12=9,
∴小林从P点出发又回到点P正好走了一个九边形,
∴α=360°÷9=40°.
故答案为40°.
19、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG的度数 度,再沿BF折叠成图c.则图中的∠CFE的度数是 度.
解:如图,延长AE到H,由于纸条是长方形,∴EH∥GF,∴∠1=∠EFG,
根据翻折不变性得∠1=∠2=15°,
∴∠2=∠EFG,∠AEG=180°﹣2×15°=150°,
又∵∠DEF=15°,∴∠2=∠EFG=15°,∠FGD=15°+15°=30°.
在梯形FCDG中,∠GFC=180°﹣30°=150°,
根据翻折不变性,∠CFE=∠GFC﹣∠GFE=150°﹣15°=135°.
故答案为:150;135.
20、如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ,则∠A2= ,∠An= .
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC=∠ABC,∠A1CD=∠ACD,然后整理得到∠A1=∠A,同理可得∠A2=∠A1,从而判断出后一个角是前一个角的,然后表示出,∠An即可.
【解答】解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠A1BC,
∴∠A1=∠A,
同理可得∠A2=∠A1=,
…,
∠An=.
故答案为:;.
三、解答题
21、如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
【分析】结论:AB∥DG.只要证明∠BAD=∠2即可.
【答案】解:结论:AB∥DG.
理由:∵AD⊥BC于D,EF⊥BC于F,
∴AD∥EF,
∴∠1=∠BAD,
∵∠1=∠2,
∴∠BAD=∠2,
∴AB∥DG.
22、如图,已知:∠ABE+∠DEB=180°,∠1=∠2,则∠F与∠G的大小关系如何?请说明理由
【分析】根据平行线的判定得出AC∥DE,根据平行线的性质得出∠CBE=∠DEB,求出∠FBE=∠GEB,根据平行线的判定得出BF∥EG即可.
【答案】解:∠F=∠G,
理由是:∵∠ABE+∠DEB=180°,
∴AC∥ED,
∴∠CBE=∠DEB,
∵∠1=∠2,
∴∠CBE﹣∠1=∠DEB﹣∠2,
即∠FBE=∠GEB,
∴BF∥EG,
∴∠F=∠G.
23、如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC向左平移5个单位得到△DEF.
(1)在正方形网格中,作出△DEF;
(2)设网格小正方形的边长为1,求平移过程中线段AC所扫过的图形面积.
【分析】(1)分别作出A,B,C的对应点D,E,F即可解决问题.
(2)根据平移过程中线段AC所扫过的图形面积=平行四边形ADFC的面积求解即可.
【答案】解:(1)△DEF如图所示.
(2)连接CF,AD.
平移过程中线段AC所扫过的图形面积=平行四边形ADFC的面积=5×3=15.
24、如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB.
(Ⅰ)若∠A=60°,则∠BOC的度数为 ;
(Ⅱ)若∠A=100°,则∠BOC的度数 ;
(Ⅲ)若∠A=α,求∠BOC的度数,并说明理由.
【分析】(Ⅰ)由三角形内角和定理以及角平分线的定义得出∠CBO+∠BCO=(180°﹣∠A),再由三角形内角和定理即可得出∠BOC的度数.
(Ⅱ)和(Ⅲ)方法同(Ⅰ).
【答案】解:(Ⅰ)∵BO、CO分别平分∠ABC和∠ACB,∠A=60°,
∴∠CBO+∠BCO=(180°﹣∠A)=(180°﹣60°)=60°,
∴∠BOC=180°﹣(∠CBO+∠BCO)=180°﹣60°=120°;
故答案为:120°;
(Ⅱ)同理,若∠A=100°,则∠BOC=180°﹣(180°﹣∠A)=90°+∠A=140°,
故答案为140°;
(Ⅲ)同理,若∠A=α,则∠BOC=180°﹣(180°﹣∠A)=90°+.
25、如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
【分析】(1)首先根据角平分线的性质可得∠BAD=∠DAC,再根据内角与外角的性质可得∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,进而得到∠EFD=∠ADC;
(2)首先根据角平分线的性质可得∠BAD=∠DAG,再根据等量代换可得∠FAE=∠BAD,然后再根据内角与外角的性质可得∠EFD=∠AEB﹣∠FAE,∠ADC=∠ABC﹣∠BAD,进而得∠EFD=∠ADC.
【答案】解:(1)∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中结论仍成立;
理由:∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB﹣∠FAE,∠ADC=∠ABC﹣∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.
26、(1)如图,在三角形纸片ABC中.∠A=64°,∠B=76°,将纸片的一角折叠,使点C落在△ABC内部,折痕为MN.如果∠1=17°,求∠2的度数;
(2)小明在(1)的解题过程中发现∠1+∠2=2∠C,小明的这个发现对任意的三角形都成立吗?请说明理由.
【分析】(1)先根据∠A=64°,∠B=76°,求出∠C的度数.再由∠1=17°可求出∠CED的度数,由三角形内角和定理及平角的性质即可求解.
(2)根据翻折变换的性质以及三角形内角和定理即可解决问题.
【答案】解:(1)∵△ABC中,∠A=64°,∠B=76°,
∴∠C=180°﹣∠A﹣∠B=180°﹣64°﹣76°=40°,
∵∠1=17°,
∴∠CNM=,
在△CMN中,∠CMN=180°﹣∠C﹣∠CNM=180°﹣40°﹣81.5°=58.5°,
∴∠2=180°﹣2∠CMN=180°﹣2×58.5°=63°.
(2)由题意可知:2∠CNM+∠1=180°,2∠CMN+∠2=180°,
∴2(∠CNM+∠CMN)+∠1+∠2=360°,
∵∠C+∠CNM+∠CMN=180°,
∴∠CMN+∠CMN=180°﹣∠C,
∴2(180°﹣∠C)=360°﹣(∠1+∠2),
∴∠1+∠2=2∠C.
27、如图,已知AB∥CD,分别探讨下面的四个图形中∠APC、∠PAB和∠PCD的关系,并请你从所得的四个关系中任选一个,说明成立的理由.
(1)图①的关系是 ;
(2)图②的关系是 ;
(3)图③的关系是 ;
(4)图④的关系是 ;
(5)图⑤的关系是 .
【分析】根据平行线的性质和三角形的外角的性质即可得到结论.
【答案】解:(1)∠APC=360°﹣∠PAB﹣∠PCD,理由如下:
过点P作EF∥AB,∵AB∥CD,EF∥AB,∴EF∥CD,
∴∠APF+∠PAB=180°,∠CPF+∠PCD=180°.
∵∠APC=∠APF+∠CPF,
∴∠APC=180°﹣∠PAB+180°﹣∠PCD=360°﹣∠PAB﹣∠PCD;
(2)∠APC=∠PAB+∠PCD,理由如下:
过点P作EF∥AB,延长AP交直线CD于E,
∵AB∥CD,EF∥AB,∴EF∥CD,∴∠APE=∠PAB,∠CPE=∠PCD.
∵∠APC=∠APE+∠CPE,∴∠APC=∠PAB+∠PCD;
(3)∠C=∠A+∠P;
理由:设AB与PC交于E,
∵AB∥CD,∴∠PEB=∠C, ∵∠PEB=∠A+∠P,∴∠C=∠A+∠P;
(4)∠PCD=∠A+∠P,
理由:延长DC交AP于E,
∵AB∥CD,∴∠PEC=∠A, ∵∠PCD=∠P+∠PEC,∴∠PCD=∠A+∠P;
(5)∠APC=180°﹣∠A+∠C.
理由:∵AB∥CD,∴∠AEC=180°﹣∠A,
∵∠APC=∠AEC+∠C,∴∠APC=180°﹣∠A+∠C.
故答案为:∠APC=360°﹣∠PAB﹣∠PCD,∠APC=∠PAB+∠PCD,∠C=∠A+∠P,
∠PCD=∠A+∠P,∠APC=180°﹣∠A+∠C.
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、如图,下列说法中错误的是( )
A.∠3和∠5是同位角 B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角 D.∠2和∠5是内错角
2、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
3、如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )
A.28° B.22° C.32° D.38°
4、如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm B.18cm C.19cm D.20cm
5、用一根长为10cm的绳子围成一个三角形,若所围成的三角形中一边的长为2cm,且另外两边长的值均为整数,则这样的围法有( )
A.1种 B.2种 C.3种 D.4种
6、如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
7、如图,直线AE∥DF,若∠ABC=120°,∠DCB=95°,则∠1+∠2的度数为( )
A.45° B.55° C.35° D.不能确定
8、小明把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于( )
A.120° B.150° C.180° D.210°
9、马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830°,则该多边形的边数是( )
A.7 B.8 C.7或8 D.无法确定
10、如图,平面内直线a∥b∥c,点A,B,C分别在直线a,b,c上,BD平分∠ABC,并且满足∠α>∠β,则∠α,∠β,∠γ关系正确的是( )
A.∠α=∠β+2∠γ B.∠α=∠β+∠γ C.∠α=2∠β﹣2∠γ D.∠α=2∠β﹣∠γ
二、填空题
11、如图,与是同位角的是__________.
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段,.则我们可以判定的依据是__________.
13、如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为_________.
14、如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_____.
15、一个等腰三角形的两边长分别为4cm和9cm,则它的周长为__cm.
16、如图,AB∥CD,则∠1+∠3—∠2的度数等于 __________.
17、若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.
18、小林从P点向西直走12米后向左转,转动的角度为α,再直走12米,又向左转α,如此重复,小林共走了108米后回到点P,则α=____.
19、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG的度数 度,再沿BF折叠成图c.则图中的∠CFE的度数是 度.
20、如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ,则∠A2= ,∠An= .
三、解答题
21、如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
22、如图,已知:∠ABE+∠DEB=180°,∠1=∠2,则∠F与∠G的大小关系如何?请说明理由
23、如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC向左平移5个单位得到△DEF.
(1)在正方形网格中,作出△DEF;
(2)设网格小正方形的边长为1,求平移过程中线段AC所扫过的图形面积.
24、如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB.
(Ⅰ)若∠A=60°,则∠BOC的度数为 ;
(Ⅱ)若∠A=100°,则∠BOC的度数 ;
(Ⅲ)若∠A=α,求∠BOC的度数,并说明理由.
25、如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
26、(1)如图,在三角形纸片ABC中.∠A=64°,∠B=76°,将纸片的一角折叠,使点C落在△ABC内部,折痕为MN.如果∠1=17°,求∠2的度数;
(2)小明在(1)的解题过程中发现∠1+∠2=2∠C,小明的这个发现对任意的三角形都成立吗?请说明理由.
27、如图,已知AB∥CD,分别探讨下面的四个图形中∠APC、∠PAB和∠PCD的关系,并请你从所得的四个关系中任选一个,说明成立的理由.
(1)图①的关系是 ;
(2)图②的关系是 ;
(3)图③的关系是 ;
(4)图④的关系是 ;
(5)图⑤的关系是 .
平面图形的认识(二)(1)(解析)
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、如图,下列说法中错误的是( )
A.∠3和∠5是同位角 B.∠4和∠5是同旁内角
C.∠2和∠4是对顶角 D.∠2和∠5是内错角
【分析】根据同位角,同旁内角,对顶角以及内错角的定义进行判断.
【答案】解:A、∠3和∠5是同位角,故本选项不符合题意.
B、∠4和∠5是同旁内角,故本选项不符合题意.
C、∠2和∠4是对顶角,故本选项不符合题意.
D、∠2和∠5不是内错角,故本选项符合题意.
故选:D.
2、如图,下列条件:①∠1=∠2;②∠4=∠5;③∠2+∠5=180°;④∠1=∠3;⑤∠6=∠1+∠2;其中能判断直线l1∥l2的有( )
A.②③④ B.②③⑤ C.②④⑤ D.②④
【答案】解:①∵∠1=∠2不能得到l1∥l2,故本条件不合题意;
②∵∠4=∠5,∴l1∥l2,故本条件符合题意;
③∵∠2+∠5=180°不能得到l1∥l2,故本条件不合题意;
④∵∠1=∠3,∴l1∥l2,故本条件符合题意;
⑤∵∠6=∠2+∠3=∠1+∠2,∴∠1=∠3,∴l1∥l2,故本条件符合题意.
故选:C.
3、如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数( )
A.28° B.22° C.32° D.38°
【分析】延长AB交CF于E,求出∠ABC,根据三角形外角性质求出∠AEC,根据平行线性质得出∠2=∠AEC,代入求出即可.
【答案】解:如图,延长AB交CF于E,
∵∠ACB=90°,∠A=30°,
∴∠ABC=60°,
∵∠1=38°,
∴∠AEC=∠ABC﹣∠1=22°,
∵GH∥EF,
∴∠2=∠AEC=22°,
故选:B.
4、如图,将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′,则四边形ABC′A′的周长为( )
A.17cm B.18cm C.19cm D.20cm
【分析】根据平移的定义求得AA'和BC'的长,则四边形的周长即可求解.
【答案】解:由题意知,BB'=CC'=AA'=3cm,
则四边形ABC'A'的周长=12+3+3=18cm.
故选:B.
5、用一根长为10cm的绳子围成一个三角形,若所围成的三角形中一边的长为2cm,且另外两边长的值均为整数,则这样的围法有( )
A.1种 B.2种 C.3种 D.4种
【分析】根据三角形的两边之和大于第三边,根据周长是10厘米,可知最长的边要小于5厘米,进而得出三条边的情况.
【答案】解:∵三角形中一边的长为2cm,且另外两边长的值均为整数,
∴三条边分别是2cm、4cm、4cm.
故选:A.
6、如图,△ABC是一块直角三角板,∠C=90°,∠A=30°,现将三角板叠放在一把直尺上,AC与直尺的两边分别交于点D、E,AB与直尺的两边分别交于点F、G,若∠1=40°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
【分析】依据平行线的性质,即可得到∠1=∠DFG=40°,再根据三角形外角性质,即可得到∠2的度数.
【答案】解:∵DF∥EG,
∴∠1=∠DFG=40°,
又∵∠A=30°,
∴∠2=∠A+∠DFG=30°+40°=70°,
故选:D.
7、如图,直线AE∥DF,若∠ABC=120°,∠DCB=95°,则∠1+∠2的度数为( )
A.45° B.55° C.35° D.不能确定
【分析】利用平行线的性质以及三角形的外角的性质解决问题即可.
【答案】解:∵AE∥DF,
∴∠3+∠4=180°,
∵∠ABC=∠1+∠3=120°,∠DCB=∠2+∠4=95°,
∴∠1+∠3+∠2+∠4=120°+95°,
∴∠1+∠2=215°﹣180°=35°,
故选:C.
8、小明把一副直角三角尺按如图所示的方式摆放在一起,其中∠E=90°,∠C=90°,∠A=45°,∠D=30°,则∠1+∠2等于( )
A.120° B.150° C.180° D.210°
【分析】根据三角形的内角和定理和三角形外角性质解答即可.
【答案】解:如图:
∵∠1=∠D+∠DOA,∠2=∠E+∠EPB,
∵∠DOA=∠COP,∠EPB=∠CPO,
∴∠1+∠2=∠D+∠E+∠COP+∠CPO=∠D+∠E+180°﹣∠C=30°+90°+180°﹣90°=210°,
故选:D.
9、马小虎在计算一个多边形的内角和时,由于粗心少算了2个内角,其和等于830°,则该多边形的边数是( )
A.7 B.8 C.7或8 D.无法确定
【分析】n边形的内角和是(n﹣2)?180°,即为180°的(n﹣2)倍,多边形的内角一定大于0度,小于180度,因而多边形中,除去2个内角外,其余内角和与180度的商加上2,以后所得的数值,比这个数值大1或2的整数就是多边形的边数.
【答案】解:设少加的2个内角和为x度,边数为n.
则(n﹣2)×180=830+x,
即(n﹣2)×180=4×180+110+x,
因此x=70,n=7或x=250,n=8.
故该多边形的边数是7或8.
故选:C.
10、如图,平面内直线a∥b∥c,点A,B,C分别在直线a,b,c上,BD平分∠ABC,并且满足∠α>∠β,则∠α,∠β,∠γ关系正确的是( )
A.∠α=∠β+2∠γ B.∠α=∠β+∠γ C.∠α=2∠β﹣2∠γ D.∠α=2∠β﹣∠γ
【分析】根据平行线的性质和角平分线的性质,可以得到∠α,∠β,∠γ的关系,本题得以解决.
【解答】解:∵直线a∥b∥c,
∴∠α=∠ABD+∠γ,∠β=∠CBD﹣∠γ,
∴∠ABD=∠α﹣∠γ,∠CBD=∠β+∠γ,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠α﹣∠γ=∠β+∠γ,
∴∠α=∠β+2∠γ,
故选:A.
二、填空题
11、如图,与是同位角的是__________.
【答案】①②
【提示】
根据同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【详解】
解:这四个图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,符合的有图①②.
故答案为:①②.
12、如图所示,小迪将两个完全相同的三角板拼在一起,沿着三角板的斜边,画出线段,.则我们可以判定的依据是__________.
【答案】内错角相等,两直线平行
【提示】
直接根据内错角相等,两直线平行即可解答.
【详解】
∵∠ADC=∠BAD=30°,
∴AB//CD(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
13、如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上,若∠ADE=125°, 则∠DBC的度数为_________.
【答案】55°
【解析】
试题提示:先根据邻补角的性质求得∠ADF的度数,再根据平行线的性质求解即可.
∵∠ADE=125°
∴∠ADF=55°
∵AD∥BC
∴∠DBC=∠ADF=55°.
14、如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是_____.
【答案】20cm.
【提示】
根据平移的性质可得DF=AE,然后判断出四边形ABFD的周长=△ABE的周长+AD+EF,然后代入数据计算即可得解.
【详解】
解:∵△ABE向右平移2cm得到△DCF,
∴DF=AE,
∴四边形ABFD的周长=AB+BE+DF+AD+EF,
=AB+BE+AE+AD+EF,
=16+AD+EF,
∵平移距离为2cm,
∴AD=EF=2cm,
∴四边形ABFD的周长=16+2+2=20cm.
故答案为20cm.
15、一个等腰三角形的两边长分别为4cm和9cm,则它的周长为__cm.
【答案】22
【提示】
底边可能是4,也可能是9,分类讨论,去掉不合条件的,然后可求周长.
【详解】
试题解析:①当腰是4cm,底边是9cm时:不满足三角形的三边关系,因此舍去.
②当底边是4cm,腰长是9cm时,能构成三角形,则其周长=4+9+9=22cm.
故填22.
16、如图,AB∥CD,则∠1+∠3—∠2的度数等于 __________.
【答案】180°
【详解】解:∵AB∥CD∴∠1=∠EFD
∵∠2+∠EFC=∠3, ∠EFD=180°-∠EFC, ∴∠1+∠3—∠2=180°
故答案为:180°
17、若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是______.
【答案】8
【详解】
解:设边数为n,由题意得,
180(n-2)=3603
解得n=8.
所以这个多边形的边数是8.
18、小林从P点向西直走12米后向左转,转动的角度为α,再直走12米,又向左转α,如此重复,小林共走了108米后回到点P,则α=____.
【答案】40°
【解析】
∵108÷12=9,
∴小林从P点出发又回到点P正好走了一个九边形,
∴α=360°÷9=40°.
故答案为40°.
19、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG的度数 度,再沿BF折叠成图c.则图中的∠CFE的度数是 度.
解:如图,延长AE到H,由于纸条是长方形,∴EH∥GF,∴∠1=∠EFG,
根据翻折不变性得∠1=∠2=15°,
∴∠2=∠EFG,∠AEG=180°﹣2×15°=150°,
又∵∠DEF=15°,∴∠2=∠EFG=15°,∠FGD=15°+15°=30°.
在梯形FCDG中,∠GFC=180°﹣30°=150°,
根据翻折不变性,∠CFE=∠GFC﹣∠GFE=150°﹣15°=135°.
故答案为:150;135.
20、如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,…,∠An﹣1BC的平分线与∠An﹣1CD的平分线交于点An.设∠A=θ,则∠A2= ,∠An= .
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,根据角平分线的定义可得∠A1BC=∠ABC,∠A1CD=∠ACD,然后整理得到∠A1=∠A,同理可得∠A2=∠A1,从而判断出后一个角是前一个角的,然后表示出,∠An即可.
【解答】解:由三角形的外角性质得,∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,
∵∠ABC的平分线与∠ACD的平分线交于点A1,
∴∠A1BC=∠ABC,∠A1CD=∠ACD,
∴∠A1+∠A1BC=(∠A+∠ABC)=∠A+∠A1BC,
∴∠A1=∠A,
同理可得∠A2=∠A1=,
…,
∠An=.
故答案为:;.
三、解答题
21、如图,AD⊥BC于D,EF⊥BC于F,∠1=∠2,AB与DG平行吗?为什么?
【分析】结论:AB∥DG.只要证明∠BAD=∠2即可.
【答案】解:结论:AB∥DG.
理由:∵AD⊥BC于D,EF⊥BC于F,
∴AD∥EF,
∴∠1=∠BAD,
∵∠1=∠2,
∴∠BAD=∠2,
∴AB∥DG.
22、如图,已知:∠ABE+∠DEB=180°,∠1=∠2,则∠F与∠G的大小关系如何?请说明理由
【分析】根据平行线的判定得出AC∥DE,根据平行线的性质得出∠CBE=∠DEB,求出∠FBE=∠GEB,根据平行线的判定得出BF∥EG即可.
【答案】解:∠F=∠G,
理由是:∵∠ABE+∠DEB=180°,
∴AC∥ED,
∴∠CBE=∠DEB,
∵∠1=∠2,
∴∠CBE﹣∠1=∠DEB﹣∠2,
即∠FBE=∠GEB,
∴BF∥EG,
∴∠F=∠G.
23、如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC向左平移5个单位得到△DEF.
(1)在正方形网格中,作出△DEF;
(2)设网格小正方形的边长为1,求平移过程中线段AC所扫过的图形面积.
【分析】(1)分别作出A,B,C的对应点D,E,F即可解决问题.
(2)根据平移过程中线段AC所扫过的图形面积=平行四边形ADFC的面积求解即可.
【答案】解:(1)△DEF如图所示.
(2)连接CF,AD.
平移过程中线段AC所扫过的图形面积=平行四边形ADFC的面积=5×3=15.
24、如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB.
(Ⅰ)若∠A=60°,则∠BOC的度数为 ;
(Ⅱ)若∠A=100°,则∠BOC的度数 ;
(Ⅲ)若∠A=α,求∠BOC的度数,并说明理由.
【分析】(Ⅰ)由三角形内角和定理以及角平分线的定义得出∠CBO+∠BCO=(180°﹣∠A),再由三角形内角和定理即可得出∠BOC的度数.
(Ⅱ)和(Ⅲ)方法同(Ⅰ).
【答案】解:(Ⅰ)∵BO、CO分别平分∠ABC和∠ACB,∠A=60°,
∴∠CBO+∠BCO=(180°﹣∠A)=(180°﹣60°)=60°,
∴∠BOC=180°﹣(∠CBO+∠BCO)=180°﹣60°=120°;
故答案为:120°;
(Ⅱ)同理,若∠A=100°,则∠BOC=180°﹣(180°﹣∠A)=90°+∠A=140°,
故答案为140°;
(Ⅲ)同理,若∠A=α,则∠BOC=180°﹣(180°﹣∠A)=90°+.
25、如图,在△ABC中,点E在AC上,∠AEB=∠ABC.
(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC;
(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?
【分析】(1)首先根据角平分线的性质可得∠BAD=∠DAC,再根据内角与外角的性质可得∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,进而得到∠EFD=∠ADC;
(2)首先根据角平分线的性质可得∠BAD=∠DAG,再根据等量代换可得∠FAE=∠BAD,然后再根据内角与外角的性质可得∠EFD=∠AEB﹣∠FAE,∠ADC=∠ABC﹣∠BAD,进而得∠EFD=∠ADC.
【答案】解:(1)∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵∠EFD=∠DAC+∠AEB,∠ADC=∠ABC+∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC;
(2)探究(1)中结论仍成立;
理由:∵AD平分∠BAG,
∴∠BAD=∠GAD,
∵∠FAE=∠GAD,
∴∠FAE=∠BAD,
∵∠EFD=∠AEB﹣∠FAE,∠ADC=∠ABC﹣∠BAD,
又∵∠AEB=∠ABC,
∴∠EFD=∠ADC.
26、(1)如图,在三角形纸片ABC中.∠A=64°,∠B=76°,将纸片的一角折叠,使点C落在△ABC内部,折痕为MN.如果∠1=17°,求∠2的度数;
(2)小明在(1)的解题过程中发现∠1+∠2=2∠C,小明的这个发现对任意的三角形都成立吗?请说明理由.
【分析】(1)先根据∠A=64°,∠B=76°,求出∠C的度数.再由∠1=17°可求出∠CED的度数,由三角形内角和定理及平角的性质即可求解.
(2)根据翻折变换的性质以及三角形内角和定理即可解决问题.
【答案】解:(1)∵△ABC中,∠A=64°,∠B=76°,
∴∠C=180°﹣∠A﹣∠B=180°﹣64°﹣76°=40°,
∵∠1=17°,
∴∠CNM=,
在△CMN中,∠CMN=180°﹣∠C﹣∠CNM=180°﹣40°﹣81.5°=58.5°,
∴∠2=180°﹣2∠CMN=180°﹣2×58.5°=63°.
(2)由题意可知:2∠CNM+∠1=180°,2∠CMN+∠2=180°,
∴2(∠CNM+∠CMN)+∠1+∠2=360°,
∵∠C+∠CNM+∠CMN=180°,
∴∠CMN+∠CMN=180°﹣∠C,
∴2(180°﹣∠C)=360°﹣(∠1+∠2),
∴∠1+∠2=2∠C.
27、如图,已知AB∥CD,分别探讨下面的四个图形中∠APC、∠PAB和∠PCD的关系,并请你从所得的四个关系中任选一个,说明成立的理由.
(1)图①的关系是 ;
(2)图②的关系是 ;
(3)图③的关系是 ;
(4)图④的关系是 ;
(5)图⑤的关系是 .
【分析】根据平行线的性质和三角形的外角的性质即可得到结论.
【答案】解:(1)∠APC=360°﹣∠PAB﹣∠PCD,理由如下:
过点P作EF∥AB,∵AB∥CD,EF∥AB,∴EF∥CD,
∴∠APF+∠PAB=180°,∠CPF+∠PCD=180°.
∵∠APC=∠APF+∠CPF,
∴∠APC=180°﹣∠PAB+180°﹣∠PCD=360°﹣∠PAB﹣∠PCD;
(2)∠APC=∠PAB+∠PCD,理由如下:
过点P作EF∥AB,延长AP交直线CD于E,
∵AB∥CD,EF∥AB,∴EF∥CD,∴∠APE=∠PAB,∠CPE=∠PCD.
∵∠APC=∠APE+∠CPE,∴∠APC=∠PAB+∠PCD;
(3)∠C=∠A+∠P;
理由:设AB与PC交于E,
∵AB∥CD,∴∠PEB=∠C, ∵∠PEB=∠A+∠P,∴∠C=∠A+∠P;
(4)∠PCD=∠A+∠P,
理由:延长DC交AP于E,
∵AB∥CD,∴∠PEC=∠A, ∵∠PCD=∠P+∠PEC,∴∠PCD=∠A+∠P;
(5)∠APC=180°﹣∠A+∠C.
理由:∵AB∥CD,∴∠AEC=180°﹣∠A,
∵∠APC=∠AEC+∠C,∴∠APC=180°﹣∠A+∠C.
故答案为:∠APC=360°﹣∠PAB﹣∠PCD,∠APC=∠PAB+∠PCD,∠C=∠A+∠P,
∠PCD=∠A+∠P,∠APC=180°﹣∠A+∠C.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
