2020-2021学年七年级数学苏科版下册期末复习提升训练第9章 整式乘法与因式分解(2)(word版含解析)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册期末复习提升训练第9章 整式乘法与因式分解(2)(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 11:13:55 | ||
图片预览




文档简介
整式乘法与因式分解(2)
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、下列各式中,计算正确的是( )
A.(﹣5an+1b)?(﹣2a)=10an+1b B.(﹣4a2b)?(﹣a2b2)?=
C.(﹣3xy)?(﹣x2z)?6xy2=3x3y3z D.
2、下列由左到右边的变形中,是因式分解的是( )
A.(x+2)(x﹣2)=x2﹣4 B.x2﹣1=x(x)
C.x2﹣4+3x=(x+2)(x﹣2)+3x D.x2﹣9=(x+3)(x﹣3)
3、已知(﹣x)(2x2﹣ax﹣1)﹣2x3+3x2中不含x的二次项,则a的值是( )
A.3 B.2 C.﹣3 D.﹣2
4、某同学在计算﹣3x2乘一个多项式时错误的计算成了加法,得到的答案是x2﹣x+1,由此可以推断正确的计算结果是( )
A.4x2﹣x+1 B.x2﹣x+1
C.﹣12x4+3x3﹣3x2 D.无法确定
5、若不管a取何值,多项式a3+2a2﹣a﹣2与(a2﹣ma+2n)(a+1)都相等,则m、n的值分别为( )
A.﹣1,﹣1 B.﹣1,1 C.1,﹣1 D.1,1
6、如果代数式,那么m的值可为( )
A.5 B.-3 C.-5或3 D.5或-3
7、若是方程组的解,则代数式的值是_______.
8、已知a,b,c是正整数,a>b,且a2﹣ab﹣ac+bc=11,则a﹣c等于( )
A.﹣1 B.﹣1或﹣11 C.1 D.1或11
9、根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后.制成的长方形铁皮(阴影部分)的面积是多少?几名同学经过讨论给出了不同的答案,其中正确的是( )
①(x﹣5)(x﹣6);②x2﹣5x﹣6(x﹣5);③x2﹣6x﹣5x;④x2﹣6x﹣5(x﹣6)
A.①②④ B.①②③④ C.① D.②④
10、如图,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置长方形内(图1,图2中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示,若长方形中边AB、AD的长度分别为m、n.设图1中阴影部分面积为S1,图2中阴影部分面积为S2.当m﹣n=2时,S1﹣S2的值为( )
A.﹣2b B.2a﹣2b C.2a D.2b
二、填空题
11、在实数范围内分解因式:4m2﹣16= .
12、计算(x2﹣4x+n)(x2+mx+8)的结果不含x3的项,那么m= .
13、若x2+mx+16是一个完全平方式,那么m的值是 .
14、若a2+b2=10,ab=﹣3,则(a﹣b)2= .
15、若多项式x2﹣px+q(p、q是常数)分解因式后,有一个因式是x+3,则3p+q的值为 .
16、若2a﹣3b=﹣1,则代数式4a2﹣6ab+3b的值为 .
17、已知ab=﹣2,a﹣b=3,则a3b﹣2a2b2+ab3的值为 .
18、若3x2﹣mx+n进行因式分解的结果为(3x+2)(x﹣1),则mn= .
19、已知a=+2012,b=+2013,c=+2014,
则代数式2(a2+b2+c2﹣ab﹣bc﹣ac)的值是 .
20、4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=S2,则a,b满足的关系式是( )
A.a=1.5b B.a=2b C.a=2.5b D.a=3b
三、解答题
21、计算题:
(1)82019×(﹣0.125)2020
(2)20202﹣2019×2021(用乘法公式进行计算);
(3)(3x﹣y)(9x2+y2)(3x+y);
(4)(a+b)(b﹣a)﹣(a﹣2b)2;
(5)先化简,再求值:[(x+3y)2﹣(x+2y)(3x﹣y)﹣11y2]÷(2x),其中x=﹣2,y=1.
22、因式分解:
(1)3ab3﹣30a2b2+75a3b; (2)a2(x﹣y)+16(y﹣x); (3)(x2+y2)2﹣4x2y2.
23、阅读下列材料:已知a2+a﹣3=0,求a2(a+4)的值.
解:∵a2=3﹣a
∴a2(a+4)=(3﹣a)(a+4)=3a+12﹣a2﹣4a=﹣a2﹣a+12
∵a2+a=3
∴﹣(a2+a)+12=﹣3+12=9
∴a2(a﹣4)=9
根据上述材料的做法,完成下列各小题:
(1)已知a2﹣a﹣10=0,求2(a+4)(a﹣5)的值.
(2)已知x2+4x﹣1=0,求代数式2x4+8x3﹣4x2﹣8x+1的值.
24、(1)已知(x+y)2=25,(x﹣y)2=9,求xy和x2+y2的值.
(2)若a2+b2=15,(a﹣b)2=3,求ab和(a+b)2的值.
25、阅读下列材料:
材料1、将一个形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n)
(1)x2+4x+3=(x+1)(x+3)(2)x2﹣4x﹣12=(x﹣6)(x+2)
材料2、因式分解:(x+y)2+2(x+y)+1
解:将“x+y”看成一个整体,令x+y=A,则原式=A2+2A+1=(A+1)2
再将“A”还原,得:原式=(x+y+1)2
上述解题用到“整体思想”,整体思想是数学解题中常见的一种思想方法,请你解答下列问题:
(1)根据材料1,把x2﹣6x+8分解因式.
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
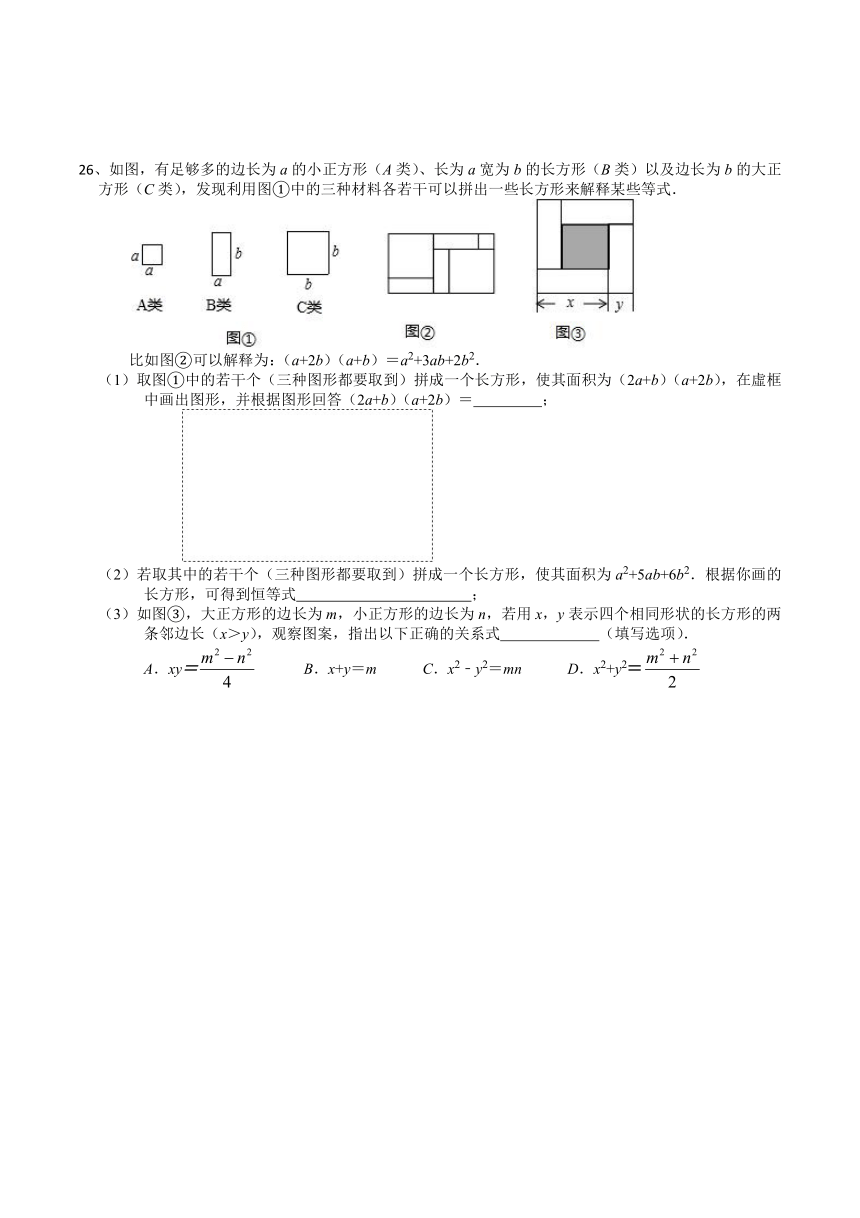
26、如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在虛框中画出图形,并根据图形回答(2a+b)(a+2b)= ;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2.根据你画的长方形,可得到恒等式 ;
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x,y表示四个相同形状的长方形的两条邻边长(x>y),观察图案,指出以下正确的关系式 (填写选项).
A.xy= B.x+y=m C.x2﹣y2=mn D.x2+y2=
整式乘法与因式分解(2)(解析)
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、下列各式中,计算正确的是( )
A.(﹣5an+1b)?(﹣2a)=10an+1b B.(﹣4a2b)?(﹣a2b2)?=
C.(﹣3xy)?(﹣x2z)?6xy2=3x3y3z D.
【分析】单项式与单项式相乘,把它们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
【答案】解:A、(﹣5an+1b)?(﹣2a)=10an+2b,此选项错误;
B、(﹣4a2b)?(﹣a2b2)?c,此选项正确;
C、(﹣3xy)?(﹣x2z)?6xy2=18x4y3z,此选项错误;
D、(2anb3)(﹣abn﹣1)=﹣an+1bn+2,此选项错误.
故选:B.
2、下列由左到右边的变形中,是因式分解的是( )
A.(x+2)(x﹣2)=x2﹣4 B.x2﹣1=x(x)
C.x2﹣4+3x=(x+2)(x﹣2)+3x D.x2﹣9=(x+3)(x﹣3)
【分析】直接利用因式分解的意义分别判断得出答案.
【解答】解:A、(x+2)(x﹣2)=x2﹣4,是多项式乘法,故此选项错误;
B、x2﹣1=(x+1)(x﹣1),故此选项错误;
C、x2﹣4+3x=(x+4)(x﹣1),故此选项错误;
D、x2﹣9=(x+3)(x﹣3),故此选项正确.
故选:D.
3、已知(﹣x)(2x2﹣ax﹣1)﹣2x3+3x2中不含x的二次项,则a的值是( )
A.3 B.2 C.﹣3 D.﹣2
【分析】先进行单项式乘多项式,再合并得到原式=﹣4x3+(a+3)x2+x,然后令二次项的系数为0即可得到a的值.
【解答】解:(﹣x)(2x2﹣ax﹣1)﹣2x3+3x2=﹣2x3+ax2+x﹣2x3+3x2
=﹣4x3+(a+3)x2+x,
因为﹣4x3+(a+3)x2+x不含x的二次项,
所以a+3=0,
所以a=﹣3.
故选:C.
4、某同学在计算﹣3x2乘一个多项式时错误的计算成了加法,得到的答案是x2﹣x+1,由此可以推断正确的计算结果是( )
A.4x2﹣x+1 B.x2﹣x+1
C.﹣12x4+3x3﹣3x2 D.无法确定
【分析】根据整式的减法法则求出多项式,根据单项式与多项式相乘的运算法则计算,得到答案.
【答案】解:x2﹣x+1﹣(﹣3x2)=x2﹣x+1+3x2=4x2﹣x+1,
﹣3x2?(4x2﹣x+1)=﹣12x4+3x3﹣3x2,
故选:C.
5、若不管a取何值,多项式a3+2a2﹣a﹣2与(a2﹣ma+2n)(a+1)都相等,则m、n的值分别为( )
A.﹣1,﹣1 B.﹣1,1 C.1,﹣1 D.1,1
【分析】根据多项式乘以多项式进行恒等计算即可.
【答案】解:多项式a3+2a2﹣a﹣2与(a2﹣ma+2n)(a+1)都相等,
(a2﹣ma+2n)(a+1)
=a3﹣ma2+2an+a2﹣ma+2n
=a3+(1﹣m)a2+(2n﹣m)a+2n
所以1﹣m=2,得m=﹣1,
2n﹣m=﹣1,得n=﹣1.
或者2n=﹣2,得n=﹣1.
故选:A.
6、如果代数式,那么m的值可为( )
A.5 B.-3 C.-5或3 D.5或-3
【答案】D
【分析】根据完全平方公式中三项式中间项等于首末两项的底数的积的2倍进行求解即可.
【详解】∵ x2+2(m-1)x+16=a2x2+2abx+b2
∴a2=1,2(m-1)=2ab,b2=16,
当a=1,b=-4时,2(m-1)=-8,则m=-3;
当a=1,b=4时,2(m-1)=8,则m=5;
当a=-1,b=-4时,2(m-1)=8,则m=5;
当a=-1,b=4时,2(m-1)=-8,则m=-3;
综上所述:m=5或-3;
故选:D.
7、若是方程组的解,则代数式的值是_______.
【答案】35
【分析】根据题意可得,再利用因式分解代入计算即可.
【解析】解:∵ 是方程组的解,∴ ,
∴ ,故填:35.
8、已知a,b,c是正整数,a>b,且a2﹣ab﹣ac+bc=11,则a﹣c等于( )
A.﹣1 B.﹣1或﹣11 C.1 D.1或11
【分析】根据因式分解的分组分解法即可求解.
【解答】解:a2﹣ab﹣ac+bc=11
(a2﹣ab)﹣(ac﹣bc)=11
a(a﹣b)﹣c(a﹣b)=11
(a﹣b)(a﹣c)=11
∵a>b,
∴a﹣b>0,a,b,c是正整数,
∴a﹣b=1或11,a﹣c=11或1.
故选:D.
9、根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后.制成的长方形铁皮(阴影部分)的面积是多少?几名同学经过讨论给出了不同的答案,其中正确的是( )
①(x﹣5)(x﹣6);②x2﹣5x﹣6(x﹣5);③x2﹣6x﹣5x;④x2﹣6x﹣5(x﹣6)
A.①②④ B.①②③④ C.① D.②④
【分析】因为正方形的边长为x,一边截去宽5的一条,另一边截去宽6的一条,所以阴影部分长方形的长和宽分别为x﹣5与x﹣6.然后根据长方形面积计算公式进行计算.
【解答】解:①由题意得:阴影部分长方形的长和宽分别为x﹣5、x﹣6,
则阴影的面积=(x﹣5)(x﹣6)=x2﹣11x+30.故该项正确;
②如图所示:
阴影部分的面积=x2﹣5x﹣6(x﹣5),故该项正确;
④如图所示:
阴影部分的面积=x2﹣6x﹣5(x﹣6),故该项正确;
③由④知本项错误.
故选:A.
10、如图,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置长方形内(图1,图2中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示,若长方形中边AB、AD的长度分别为m、n.设图1中阴影部分面积为S1,图2中阴影部分面积为S2.当m﹣n=2时,S1﹣S2的值为( )
A.﹣2b B.2a﹣2b C.2a D.2b
【分析】根据平移的知识和面积的定义,列出算式S1﹣S2=
n(m﹣a)+(a﹣b)(n﹣a)﹣[m(n﹣a)+(a﹣b)(m﹣a)],再去括号,合并同类项即可求解.
【解答】解:图1中阴影部分的面积S1=n(m﹣a)+(a﹣b)(n﹣a),
图2中阴影部分的面积S2=m(n﹣a)+(a﹣b)(m﹣a),
S1﹣S2=n(m﹣a)+(a﹣b)(n﹣a)﹣[m(n﹣a)+(a﹣b)(m﹣a)]
=nm﹣na+n(a﹣b)﹣a(a﹣b)﹣mn+am﹣m(a﹣b)+a(a﹣b)
=b(m﹣n)=2b.
故选:D.
二、填空题
11、在实数范围内分解因式:4m2﹣16= .
【分析】原式提取公因式,再利用平方差公式分解即可.
【解答】解:原式=4(m2﹣4)=4(m+2)(m﹣2),
故答案为:4(m+2)(m﹣2)
12、计算(x2﹣4x+n)(x2+mx+8)的结果不含x3的项,那么m= .
【解析】(x2﹣4x+n)(x2+mx+8)=x4+mx3+8x2﹣4x3﹣4mx2﹣32x+nx2+mnx+8n
=x4+(m﹣4)x3+(8﹣4m+n)x2+(mn﹣32)x+8n,
∵结果不含x3的项,∴m﹣4=0,解得,m=4,故答案为:4.
13、若x2+mx+16是一个完全平方式,那么m的值是 .
【分析】利用完全平方公式的结构特征计算即可求出m的值.
【解答】解:∵若x2+mx+16是一个完全平方式,
∴m=±8,
故答案为:±8
14、若a2+b2=10,ab=﹣3,则(a﹣b)2= .
【分析】根据完全平方公式解答即可.
【解答】解:∵(a﹣b)2=a2﹣2ab+b2,a2+b2=10,ab=﹣3,
∴(a﹣b)2=10﹣2×(﹣3)=10+6=16.故答案为:16.
15、若多项式x2﹣px+q(p、q是常数)分解因式后,有一个因式是x+3,则3p+q的值为 .
【分析】设另一个因式为x+a,因为整式乘法是因式分解的逆运算,所以将两个因式相乘后结果得x2﹣px+q,根据各项系数相等列式,计算可得3p+q的值.
【解析】设另一个因式为x+a,
则x2﹣px+q=(x+3)(x+a)=x2+ax+3x+3a=x2+(a+3)x+3a, 由此可得
由①得:a=﹣p﹣3③,
把③代入②得:﹣3p﹣9=q,
3p+q=﹣9,
故答案为:﹣9.
16、若2a﹣3b=﹣1,则代数式4a2﹣6ab+3b的值为 .
【分析】由已知字母a、b的系数为2、﹣3,代数式中前二项的北系娄秋4、﹣6,提取此二项的公因式2a后,代入求值变形得﹣2a+3b,与已知条件互为相反数,可求出代数式的值为1.
【解答】解:∵2a﹣3b=﹣1,∴4a2﹣6ab+3b=2a(2a﹣3b)+3b=2a×(﹣1)+3b
=﹣2a+3b=﹣(2a﹣3b)=﹣(﹣1)=1。故答案为1
17、已知ab=﹣2,a﹣b=3,则a3b﹣2a2b2+ab3的值为 .
【分析】本题要求代数式a3b﹣2a2b2+ab3的值,而代数式a3b﹣2a2b2+ab3恰好可以分解为两个已知条件ab,(a﹣b)的乘积,因此可以运用整体的数学思想来解答.
【解答】解:a3b﹣2a2b2+ab3=ab(a2﹣2ab+b2)
=ab(a﹣b)2
当a﹣b=3,ab=﹣2时,原式=﹣2×32=﹣18,
故答案为:﹣18
18、若3x2﹣mx+n进行因式分解的结果为(3x+2)(x﹣1),则mn= .
【分析】将(3x+2)(x﹣1)展开,则3x2﹣mx+n=3x2﹣x﹣2,从而求出m、n的值,代入计算可得答案.
【解答】解:∵(3x+2)(x﹣1)=3x2﹣x﹣2,∴3x2﹣mx+n=3x2﹣x﹣2,
∴m=1,n=﹣2,∴mn=﹣2,故答案为:﹣2.
19、已知a=+2012,b=+2013,c=+2014,
则代数式2(a2+b2+c2﹣ab﹣bc﹣ac)的值是 .
【分析】根据a、b、c的值,分别求出a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,c﹣b=1进而把代数式2(a2+b2+c2﹣ab﹣bc﹣ac)分组分解,即可得出答案.
【解答】∵a=+2012,b=+2013,c=+2014,
∴a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,c﹣b=1,
∴2(a2+b2+c2﹣ab﹣bc﹣ac),
=2[a(a﹣b)+b(b﹣c)+c(c﹣a)],
=2(﹣a﹣b+2c),
=2[(c﹣a)+(c﹣b)],
=2×3,
=6.
故答案为:6.
20、4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=S2,则a,b满足的关系式是( )
A.a=1.5b B.a=2b C.a=2.5b D.a=3b
【分析】先用含有a、b的代数式分别表示S2=2ab+2b2,S1=a2﹣b2,再根据S1=S2,整理可得结论.
【解析】由题意可得:S2=4b(a+b)=2b(a+b);
S1=(a+b)2﹣S2=(a+b)2﹣(2ab+2b2)=a2+2ab+b2﹣2ab﹣2b2=a2﹣b2;
∵S1=S2,∴2b(a+b)=a2﹣b2,∴2b(a+b)=(a﹣b)(a+b),
∵a+b>0,∴2b=a﹣b,∴a=3b.故选:D.
三、解答题
21、计算题:
(1)82019×(﹣0.125)2020
(2)20202﹣2019×2021(用乘法公式进行计算);
(3)(3x﹣y)(9x2+y2)(3x+y);
(4)(a+b)(b﹣a)﹣(a﹣2b)2;
(5)先化简,再求值:[(x+3y)2﹣(x+2y)(3x﹣y)﹣11y2]÷(2x),其中x=﹣2,y=1.
【分析】(1)将原式变形为(﹣0.125)2019×82019×(﹣0.125),再逆用积的乘方变形、计算可得;
(2)原式变形后,利用平方差公式计算即可求出值;
(3)原式结合后,利用平方差公式计算即可得到结果;
(4)原式利用平方差公式,以及完全平方公式化简,去括号合并即可得到结果;
(5)原式中括号中利用完全平方公式,以及多项式乘以多项式法则计算,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】解:(1)82019×(﹣0.125)2020
=(﹣0.125)2019×82019×(﹣0.125)
=(﹣0.125×8)2019×(﹣0.125)
=0.125;
(2)20202﹣2019×2021
=20202﹣(2020﹣1)×(2020+1)
=20202﹣20202+1
=1;
(3)(3x﹣y)(9x2+y2)(3x+y)
=(3x﹣y)(3x+y)(9x2+y2)
=(9x2﹣y2)(9x2+y2)
=81x4﹣y4;
(4)(a+b)(b﹣a)﹣(a﹣2b)2
=a2﹣b2﹣(a2﹣4ab+4b2)
=a2﹣b2﹣a2+4ab﹣4b2
=4ab﹣5b2;
(5)[(x+3y)2﹣(x+2y)(3x﹣y)﹣11y2]÷(2x)
=(x2+6xy+9y2﹣3x2+xy﹣6xy+2y2﹣11y2)÷2x
=(﹣2x2+xy)÷2x
=﹣x+y,
当x=﹣2,y=1时,原式=.
22、因式分解:
(1)3ab3﹣30a2b2+75a3b; (2)a2(x﹣y)+16(y﹣x); (3)(x2+y2)2﹣4x2y2.
【分析】(1)原式提取公因式,再利用完全平方公式分解即可;
(2)原式变形后,提取公因式,再利用平方差公式分解即可;
(3)原式利用平方差公式,以及完全平方公式分解即可.
【解答】解:(1)3ab3﹣30a2b2+75a3b=3ab(b2﹣10ab+25a2)=3ab(b﹣5a)2;
(2)a2(x﹣y)+16(y﹣x)=(x﹣y)(a2﹣16)=(x﹣y)(a+4)(a﹣4);
(3)(x2+y2)2﹣4x2y2=(x2+y2+2xy)(x2+y2﹣2xy)=(x+y)2(x﹣y)2.
23、阅读下列材料:已知a2+a﹣3=0,求a2(a+4)的值.
解:∵a2=3﹣a
∴a2(a+4)=(3﹣a)(a+4)=3a+12﹣a2﹣4a=﹣a2﹣a+12
∵a2+a=3
∴﹣(a2+a)+12=﹣3+12=9
∴a2(a﹣4)=9
根据上述材料的做法,完成下列各小题:
(1)已知a2﹣a﹣10=0,求2(a+4)(a﹣5)的值.
(2)已知x2+4x﹣1=0,求代数式2x4+8x3﹣4x2﹣8x+1的值.
【分析】(1)直接将原式变形进而把已知代入得出答案;
(2)直接将原式变形进而把已知代入得出答案.
【解答】解:(1)∵a2﹣a﹣10=0,∴a2﹣a=10,
2(a+4)(a﹣5)=2(a2﹣a﹣20)=2×(10﹣20)=﹣20;
(2)∵x2+4x﹣1=0,∴x2+4x=1,
2x4+8x3﹣4x2﹣8x+1=2x2(x2+4x)﹣4x2﹣8x+1=2x2﹣4x2﹣8x+1
=﹣2x2﹣8x+1=﹣2(x2+4x)+1=﹣2+1=﹣1.
24、(1)已知(x+y)2=25,(x﹣y)2=9,求xy和x2+y2的值.
(2)若a2+b2=15,(a﹣b)2=3,求ab和(a+b)2的值.
【分析】(1)首先去括号,进而得出x2+y2的值,即可求出xy的值;
(2)直接利用完全平方公式配方进而得出a,b的值,即可得出答案.
【解答】解:(1)∵(x+y)2=25,(x﹣y)2=9,
∴x2+2xy+y2=25①,x2﹣2xy+y2=9②,
∴①+②得:2(x2+y2)=34,
∴x2+y2=17,
∴17+2xy=25,
∴xy=4;
(2)∵(a﹣b)2=3,
∴a2﹣2ab+b2=3,
∵a2+b2=15,
∴15﹣2ab=3,
∴﹣2ab=﹣12,
∴ab=6,
∵a2+b2=15,
∴a2+2ab+b2=15+12,
∴(a+b)2=27.
25、阅读下列材料:
材料1、将一个形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n)
(1)x2+4x+3=(x+1)(x+3)(2)x2﹣4x﹣12=(x﹣6)(x+2)
材料2、因式分解:(x+y)2+2(x+y)+1
解:将“x+y”看成一个整体,令x+y=A,则原式=A2+2A+1=(A+1)2
再将“A”还原,得:原式=(x+y+1)2
上述解题用到“整体思想”,整体思想是数学解题中常见的一种思想方法,请你解答下列问题:
(1)根据材料1,把x2﹣6x+8分解因式.
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
【分析】(1)利用十字相乘法变形即可得;
(2)①根据材料2的整体思想可以对(x﹣y)2+4(x﹣y)+3分解因式;
②根据材料1和材料2可以对m(m+2)(m2+2m﹣2)﹣3分解因式.
【解答】解:(1)x2﹣6x+8=(x﹣2)(x﹣4);
(2)①令A=x﹣y,
则原式=A2+4A+3=(A+1)(A+3),
所以(x﹣y)2+4(x﹣y)+3=(x﹣y+1)(x﹣y+3);
②令B=m2+2m,则原式=B(B﹣2)﹣3=B2﹣2B﹣3=(B+1)(B﹣3),
所以原式=(m2+2m+1)(m2+2m﹣3)=(m+1)2(m﹣1)(m+3).
26、如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在虛框中画出图形,并根据图形回答(2a+b)(a+2b)= ;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2.根据你画的长方形,可得到恒等式 ;
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x,y表示四个相同形状的长方形的两条邻边长(x>y),观察图案,指出以下正确的关系式 (填写选项).
A.xy= B.x+y=m C.x2﹣y2=mn D.x2+y2=
【分析】(1)计算(2a+b)(a+2b)的结果,可知需要A、B、C型的纸片的张数,进而画出拼图;
(2)a2+5ab+6b2即用A型的1张,B型的5张,C型的6张,可以拼图,得出等式;
(3)根据m、n与x、y之间的关系,利用恒等变形,可得结论.
【解答】解:(1)(2a+b)(a+2b)=2a2+5ab+2b2,
故答案为:2a2+5ab+2b2;拼图如图所示:
(2)a2+5ab+6b2即用A型的1张,B型的5张,C型的6张,可以拼成如图所示的图形,
因此可得等式:a2+5ab+6b2=(a+3b)(a+2b),
故答案为:a2+5ab+6b2=(a+3b)(a+2b);
(3)由图③可知,m=x+y,n=x﹣y,因此有m+n=2x,m﹣n=2y,mn=(x+y)(x﹣y)=x2﹣y2;
故答案为:A、B、C、D.
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、下列各式中,计算正确的是( )
A.(﹣5an+1b)?(﹣2a)=10an+1b B.(﹣4a2b)?(﹣a2b2)?=
C.(﹣3xy)?(﹣x2z)?6xy2=3x3y3z D.
2、下列由左到右边的变形中,是因式分解的是( )
A.(x+2)(x﹣2)=x2﹣4 B.x2﹣1=x(x)
C.x2﹣4+3x=(x+2)(x﹣2)+3x D.x2﹣9=(x+3)(x﹣3)
3、已知(﹣x)(2x2﹣ax﹣1)﹣2x3+3x2中不含x的二次项,则a的值是( )
A.3 B.2 C.﹣3 D.﹣2
4、某同学在计算﹣3x2乘一个多项式时错误的计算成了加法,得到的答案是x2﹣x+1,由此可以推断正确的计算结果是( )
A.4x2﹣x+1 B.x2﹣x+1
C.﹣12x4+3x3﹣3x2 D.无法确定
5、若不管a取何值,多项式a3+2a2﹣a﹣2与(a2﹣ma+2n)(a+1)都相等,则m、n的值分别为( )
A.﹣1,﹣1 B.﹣1,1 C.1,﹣1 D.1,1
6、如果代数式,那么m的值可为( )
A.5 B.-3 C.-5或3 D.5或-3
7、若是方程组的解,则代数式的值是_______.
8、已知a,b,c是正整数,a>b,且a2﹣ab﹣ac+bc=11,则a﹣c等于( )
A.﹣1 B.﹣1或﹣11 C.1 D.1或11
9、根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后.制成的长方形铁皮(阴影部分)的面积是多少?几名同学经过讨论给出了不同的答案,其中正确的是( )
①(x﹣5)(x﹣6);②x2﹣5x﹣6(x﹣5);③x2﹣6x﹣5x;④x2﹣6x﹣5(x﹣6)
A.①②④ B.①②③④ C.① D.②④
10、如图,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置长方形内(图1,图2中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示,若长方形中边AB、AD的长度分别为m、n.设图1中阴影部分面积为S1,图2中阴影部分面积为S2.当m﹣n=2时,S1﹣S2的值为( )
A.﹣2b B.2a﹣2b C.2a D.2b
二、填空题
11、在实数范围内分解因式:4m2﹣16= .
12、计算(x2﹣4x+n)(x2+mx+8)的结果不含x3的项,那么m= .
13、若x2+mx+16是一个完全平方式,那么m的值是 .
14、若a2+b2=10,ab=﹣3,则(a﹣b)2= .
15、若多项式x2﹣px+q(p、q是常数)分解因式后,有一个因式是x+3,则3p+q的值为 .
16、若2a﹣3b=﹣1,则代数式4a2﹣6ab+3b的值为 .
17、已知ab=﹣2,a﹣b=3,则a3b﹣2a2b2+ab3的值为 .
18、若3x2﹣mx+n进行因式分解的结果为(3x+2)(x﹣1),则mn= .
19、已知a=+2012,b=+2013,c=+2014,
则代数式2(a2+b2+c2﹣ab﹣bc﹣ac)的值是 .
20、4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=S2,则a,b满足的关系式是( )
A.a=1.5b B.a=2b C.a=2.5b D.a=3b
三、解答题
21、计算题:
(1)82019×(﹣0.125)2020
(2)20202﹣2019×2021(用乘法公式进行计算);
(3)(3x﹣y)(9x2+y2)(3x+y);
(4)(a+b)(b﹣a)﹣(a﹣2b)2;
(5)先化简,再求值:[(x+3y)2﹣(x+2y)(3x﹣y)﹣11y2]÷(2x),其中x=﹣2,y=1.
22、因式分解:
(1)3ab3﹣30a2b2+75a3b; (2)a2(x﹣y)+16(y﹣x); (3)(x2+y2)2﹣4x2y2.
23、阅读下列材料:已知a2+a﹣3=0,求a2(a+4)的值.
解:∵a2=3﹣a
∴a2(a+4)=(3﹣a)(a+4)=3a+12﹣a2﹣4a=﹣a2﹣a+12
∵a2+a=3
∴﹣(a2+a)+12=﹣3+12=9
∴a2(a﹣4)=9
根据上述材料的做法,完成下列各小题:
(1)已知a2﹣a﹣10=0,求2(a+4)(a﹣5)的值.
(2)已知x2+4x﹣1=0,求代数式2x4+8x3﹣4x2﹣8x+1的值.
24、(1)已知(x+y)2=25,(x﹣y)2=9,求xy和x2+y2的值.
(2)若a2+b2=15,(a﹣b)2=3,求ab和(a+b)2的值.
25、阅读下列材料:
材料1、将一个形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n)
(1)x2+4x+3=(x+1)(x+3)(2)x2﹣4x﹣12=(x﹣6)(x+2)
材料2、因式分解:(x+y)2+2(x+y)+1
解:将“x+y”看成一个整体,令x+y=A,则原式=A2+2A+1=(A+1)2
再将“A”还原,得:原式=(x+y+1)2
上述解题用到“整体思想”,整体思想是数学解题中常见的一种思想方法,请你解答下列问题:
(1)根据材料1,把x2﹣6x+8分解因式.
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
26、如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在虛框中画出图形,并根据图形回答(2a+b)(a+2b)= ;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2.根据你画的长方形,可得到恒等式 ;
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x,y表示四个相同形状的长方形的两条邻边长(x>y),观察图案,指出以下正确的关系式 (填写选项).
A.xy= B.x+y=m C.x2﹣y2=mn D.x2+y2=
整式乘法与因式分解(2)(解析)
-2020-2021学年七年级数学下册期末复习提升训练(苏科版)
一、选择题
1、下列各式中,计算正确的是( )
A.(﹣5an+1b)?(﹣2a)=10an+1b B.(﹣4a2b)?(﹣a2b2)?=
C.(﹣3xy)?(﹣x2z)?6xy2=3x3y3z D.
【分析】单项式与单项式相乘,把它们的系数,相同字母分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
【答案】解:A、(﹣5an+1b)?(﹣2a)=10an+2b,此选项错误;
B、(﹣4a2b)?(﹣a2b2)?c,此选项正确;
C、(﹣3xy)?(﹣x2z)?6xy2=18x4y3z,此选项错误;
D、(2anb3)(﹣abn﹣1)=﹣an+1bn+2,此选项错误.
故选:B.
2、下列由左到右边的变形中,是因式分解的是( )
A.(x+2)(x﹣2)=x2﹣4 B.x2﹣1=x(x)
C.x2﹣4+3x=(x+2)(x﹣2)+3x D.x2﹣9=(x+3)(x﹣3)
【分析】直接利用因式分解的意义分别判断得出答案.
【解答】解:A、(x+2)(x﹣2)=x2﹣4,是多项式乘法,故此选项错误;
B、x2﹣1=(x+1)(x﹣1),故此选项错误;
C、x2﹣4+3x=(x+4)(x﹣1),故此选项错误;
D、x2﹣9=(x+3)(x﹣3),故此选项正确.
故选:D.
3、已知(﹣x)(2x2﹣ax﹣1)﹣2x3+3x2中不含x的二次项,则a的值是( )
A.3 B.2 C.﹣3 D.﹣2
【分析】先进行单项式乘多项式,再合并得到原式=﹣4x3+(a+3)x2+x,然后令二次项的系数为0即可得到a的值.
【解答】解:(﹣x)(2x2﹣ax﹣1)﹣2x3+3x2=﹣2x3+ax2+x﹣2x3+3x2
=﹣4x3+(a+3)x2+x,
因为﹣4x3+(a+3)x2+x不含x的二次项,
所以a+3=0,
所以a=﹣3.
故选:C.
4、某同学在计算﹣3x2乘一个多项式时错误的计算成了加法,得到的答案是x2﹣x+1,由此可以推断正确的计算结果是( )
A.4x2﹣x+1 B.x2﹣x+1
C.﹣12x4+3x3﹣3x2 D.无法确定
【分析】根据整式的减法法则求出多项式,根据单项式与多项式相乘的运算法则计算,得到答案.
【答案】解:x2﹣x+1﹣(﹣3x2)=x2﹣x+1+3x2=4x2﹣x+1,
﹣3x2?(4x2﹣x+1)=﹣12x4+3x3﹣3x2,
故选:C.
5、若不管a取何值,多项式a3+2a2﹣a﹣2与(a2﹣ma+2n)(a+1)都相等,则m、n的值分别为( )
A.﹣1,﹣1 B.﹣1,1 C.1,﹣1 D.1,1
【分析】根据多项式乘以多项式进行恒等计算即可.
【答案】解:多项式a3+2a2﹣a﹣2与(a2﹣ma+2n)(a+1)都相等,
(a2﹣ma+2n)(a+1)
=a3﹣ma2+2an+a2﹣ma+2n
=a3+(1﹣m)a2+(2n﹣m)a+2n
所以1﹣m=2,得m=﹣1,
2n﹣m=﹣1,得n=﹣1.
或者2n=﹣2,得n=﹣1.
故选:A.
6、如果代数式,那么m的值可为( )
A.5 B.-3 C.-5或3 D.5或-3
【答案】D
【分析】根据完全平方公式中三项式中间项等于首末两项的底数的积的2倍进行求解即可.
【详解】∵ x2+2(m-1)x+16=a2x2+2abx+b2
∴a2=1,2(m-1)=2ab,b2=16,
当a=1,b=-4时,2(m-1)=-8,则m=-3;
当a=1,b=4时,2(m-1)=8,则m=5;
当a=-1,b=-4时,2(m-1)=8,则m=5;
当a=-1,b=4时,2(m-1)=-8,则m=-3;
综上所述:m=5或-3;
故选:D.
7、若是方程组的解,则代数式的值是_______.
【答案】35
【分析】根据题意可得,再利用因式分解代入计算即可.
【解析】解:∵ 是方程组的解,∴ ,
∴ ,故填:35.
8、已知a,b,c是正整数,a>b,且a2﹣ab﹣ac+bc=11,则a﹣c等于( )
A.﹣1 B.﹣1或﹣11 C.1 D.1或11
【分析】根据因式分解的分组分解法即可求解.
【解答】解:a2﹣ab﹣ac+bc=11
(a2﹣ab)﹣(ac﹣bc)=11
a(a﹣b)﹣c(a﹣b)=11
(a﹣b)(a﹣c)=11
∵a>b,
∴a﹣b>0,a,b,c是正整数,
∴a﹣b=1或11,a﹣c=11或1.
故选:D.
9、根据需要将一块边长为x的正方形铁皮按如图的方法截去一部分后.制成的长方形铁皮(阴影部分)的面积是多少?几名同学经过讨论给出了不同的答案,其中正确的是( )
①(x﹣5)(x﹣6);②x2﹣5x﹣6(x﹣5);③x2﹣6x﹣5x;④x2﹣6x﹣5(x﹣6)
A.①②④ B.①②③④ C.① D.②④
【分析】因为正方形的边长为x,一边截去宽5的一条,另一边截去宽6的一条,所以阴影部分长方形的长和宽分别为x﹣5与x﹣6.然后根据长方形面积计算公式进行计算.
【解答】解:①由题意得:阴影部分长方形的长和宽分别为x﹣5、x﹣6,
则阴影的面积=(x﹣5)(x﹣6)=x2﹣11x+30.故该项正确;
②如图所示:
阴影部分的面积=x2﹣5x﹣6(x﹣5),故该项正确;
④如图所示:
阴影部分的面积=x2﹣6x﹣5(x﹣6),故该项正确;
③由④知本项错误.
故选:A.
10、如图,将两张边长分别为a和b(a>b)的正方形纸片按图1,图2两种方式放置长方形内(图1,图2中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示,若长方形中边AB、AD的长度分别为m、n.设图1中阴影部分面积为S1,图2中阴影部分面积为S2.当m﹣n=2时,S1﹣S2的值为( )
A.﹣2b B.2a﹣2b C.2a D.2b
【分析】根据平移的知识和面积的定义,列出算式S1﹣S2=
n(m﹣a)+(a﹣b)(n﹣a)﹣[m(n﹣a)+(a﹣b)(m﹣a)],再去括号,合并同类项即可求解.
【解答】解:图1中阴影部分的面积S1=n(m﹣a)+(a﹣b)(n﹣a),
图2中阴影部分的面积S2=m(n﹣a)+(a﹣b)(m﹣a),
S1﹣S2=n(m﹣a)+(a﹣b)(n﹣a)﹣[m(n﹣a)+(a﹣b)(m﹣a)]
=nm﹣na+n(a﹣b)﹣a(a﹣b)﹣mn+am﹣m(a﹣b)+a(a﹣b)
=b(m﹣n)=2b.
故选:D.
二、填空题
11、在实数范围内分解因式:4m2﹣16= .
【分析】原式提取公因式,再利用平方差公式分解即可.
【解答】解:原式=4(m2﹣4)=4(m+2)(m﹣2),
故答案为:4(m+2)(m﹣2)
12、计算(x2﹣4x+n)(x2+mx+8)的结果不含x3的项,那么m= .
【解析】(x2﹣4x+n)(x2+mx+8)=x4+mx3+8x2﹣4x3﹣4mx2﹣32x+nx2+mnx+8n
=x4+(m﹣4)x3+(8﹣4m+n)x2+(mn﹣32)x+8n,
∵结果不含x3的项,∴m﹣4=0,解得,m=4,故答案为:4.
13、若x2+mx+16是一个完全平方式,那么m的值是 .
【分析】利用完全平方公式的结构特征计算即可求出m的值.
【解答】解:∵若x2+mx+16是一个完全平方式,
∴m=±8,
故答案为:±8
14、若a2+b2=10,ab=﹣3,则(a﹣b)2= .
【分析】根据完全平方公式解答即可.
【解答】解:∵(a﹣b)2=a2﹣2ab+b2,a2+b2=10,ab=﹣3,
∴(a﹣b)2=10﹣2×(﹣3)=10+6=16.故答案为:16.
15、若多项式x2﹣px+q(p、q是常数)分解因式后,有一个因式是x+3,则3p+q的值为 .
【分析】设另一个因式为x+a,因为整式乘法是因式分解的逆运算,所以将两个因式相乘后结果得x2﹣px+q,根据各项系数相等列式,计算可得3p+q的值.
【解析】设另一个因式为x+a,
则x2﹣px+q=(x+3)(x+a)=x2+ax+3x+3a=x2+(a+3)x+3a, 由此可得
由①得:a=﹣p﹣3③,
把③代入②得:﹣3p﹣9=q,
3p+q=﹣9,
故答案为:﹣9.
16、若2a﹣3b=﹣1,则代数式4a2﹣6ab+3b的值为 .
【分析】由已知字母a、b的系数为2、﹣3,代数式中前二项的北系娄秋4、﹣6,提取此二项的公因式2a后,代入求值变形得﹣2a+3b,与已知条件互为相反数,可求出代数式的值为1.
【解答】解:∵2a﹣3b=﹣1,∴4a2﹣6ab+3b=2a(2a﹣3b)+3b=2a×(﹣1)+3b
=﹣2a+3b=﹣(2a﹣3b)=﹣(﹣1)=1。故答案为1
17、已知ab=﹣2,a﹣b=3,则a3b﹣2a2b2+ab3的值为 .
【分析】本题要求代数式a3b﹣2a2b2+ab3的值,而代数式a3b﹣2a2b2+ab3恰好可以分解为两个已知条件ab,(a﹣b)的乘积,因此可以运用整体的数学思想来解答.
【解答】解:a3b﹣2a2b2+ab3=ab(a2﹣2ab+b2)
=ab(a﹣b)2
当a﹣b=3,ab=﹣2时,原式=﹣2×32=﹣18,
故答案为:﹣18
18、若3x2﹣mx+n进行因式分解的结果为(3x+2)(x﹣1),则mn= .
【分析】将(3x+2)(x﹣1)展开,则3x2﹣mx+n=3x2﹣x﹣2,从而求出m、n的值,代入计算可得答案.
【解答】解:∵(3x+2)(x﹣1)=3x2﹣x﹣2,∴3x2﹣mx+n=3x2﹣x﹣2,
∴m=1,n=﹣2,∴mn=﹣2,故答案为:﹣2.
19、已知a=+2012,b=+2013,c=+2014,
则代数式2(a2+b2+c2﹣ab﹣bc﹣ac)的值是 .
【分析】根据a、b、c的值,分别求出a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,c﹣b=1进而把代数式2(a2+b2+c2﹣ab﹣bc﹣ac)分组分解,即可得出答案.
【解答】∵a=+2012,b=+2013,c=+2014,
∴a﹣b=﹣1,b﹣c=﹣1,c﹣a=2,c﹣b=1,
∴2(a2+b2+c2﹣ab﹣bc﹣ac),
=2[a(a﹣b)+b(b﹣c)+c(c﹣a)],
=2(﹣a﹣b+2c),
=2[(c﹣a)+(c﹣b)],
=2×3,
=6.
故答案为:6.
20、4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=S2,则a,b满足的关系式是( )
A.a=1.5b B.a=2b C.a=2.5b D.a=3b
【分析】先用含有a、b的代数式分别表示S2=2ab+2b2,S1=a2﹣b2,再根据S1=S2,整理可得结论.
【解析】由题意可得:S2=4b(a+b)=2b(a+b);
S1=(a+b)2﹣S2=(a+b)2﹣(2ab+2b2)=a2+2ab+b2﹣2ab﹣2b2=a2﹣b2;
∵S1=S2,∴2b(a+b)=a2﹣b2,∴2b(a+b)=(a﹣b)(a+b),
∵a+b>0,∴2b=a﹣b,∴a=3b.故选:D.
三、解答题
21、计算题:
(1)82019×(﹣0.125)2020
(2)20202﹣2019×2021(用乘法公式进行计算);
(3)(3x﹣y)(9x2+y2)(3x+y);
(4)(a+b)(b﹣a)﹣(a﹣2b)2;
(5)先化简,再求值:[(x+3y)2﹣(x+2y)(3x﹣y)﹣11y2]÷(2x),其中x=﹣2,y=1.
【分析】(1)将原式变形为(﹣0.125)2019×82019×(﹣0.125),再逆用积的乘方变形、计算可得;
(2)原式变形后,利用平方差公式计算即可求出值;
(3)原式结合后,利用平方差公式计算即可得到结果;
(4)原式利用平方差公式,以及完全平方公式化简,去括号合并即可得到结果;
(5)原式中括号中利用完全平方公式,以及多项式乘以多项式法则计算,去括号合并后利用多项式除以单项式法则计算得到最简结果,把x与y的值代入计算即可求出值.
【解答】解:(1)82019×(﹣0.125)2020
=(﹣0.125)2019×82019×(﹣0.125)
=(﹣0.125×8)2019×(﹣0.125)
=0.125;
(2)20202﹣2019×2021
=20202﹣(2020﹣1)×(2020+1)
=20202﹣20202+1
=1;
(3)(3x﹣y)(9x2+y2)(3x+y)
=(3x﹣y)(3x+y)(9x2+y2)
=(9x2﹣y2)(9x2+y2)
=81x4﹣y4;
(4)(a+b)(b﹣a)﹣(a﹣2b)2
=a2﹣b2﹣(a2﹣4ab+4b2)
=a2﹣b2﹣a2+4ab﹣4b2
=4ab﹣5b2;
(5)[(x+3y)2﹣(x+2y)(3x﹣y)﹣11y2]÷(2x)
=(x2+6xy+9y2﹣3x2+xy﹣6xy+2y2﹣11y2)÷2x
=(﹣2x2+xy)÷2x
=﹣x+y,
当x=﹣2,y=1时,原式=.
22、因式分解:
(1)3ab3﹣30a2b2+75a3b; (2)a2(x﹣y)+16(y﹣x); (3)(x2+y2)2﹣4x2y2.
【分析】(1)原式提取公因式,再利用完全平方公式分解即可;
(2)原式变形后,提取公因式,再利用平方差公式分解即可;
(3)原式利用平方差公式,以及完全平方公式分解即可.
【解答】解:(1)3ab3﹣30a2b2+75a3b=3ab(b2﹣10ab+25a2)=3ab(b﹣5a)2;
(2)a2(x﹣y)+16(y﹣x)=(x﹣y)(a2﹣16)=(x﹣y)(a+4)(a﹣4);
(3)(x2+y2)2﹣4x2y2=(x2+y2+2xy)(x2+y2﹣2xy)=(x+y)2(x﹣y)2.
23、阅读下列材料:已知a2+a﹣3=0,求a2(a+4)的值.
解:∵a2=3﹣a
∴a2(a+4)=(3﹣a)(a+4)=3a+12﹣a2﹣4a=﹣a2﹣a+12
∵a2+a=3
∴﹣(a2+a)+12=﹣3+12=9
∴a2(a﹣4)=9
根据上述材料的做法,完成下列各小题:
(1)已知a2﹣a﹣10=0,求2(a+4)(a﹣5)的值.
(2)已知x2+4x﹣1=0,求代数式2x4+8x3﹣4x2﹣8x+1的值.
【分析】(1)直接将原式变形进而把已知代入得出答案;
(2)直接将原式变形进而把已知代入得出答案.
【解答】解:(1)∵a2﹣a﹣10=0,∴a2﹣a=10,
2(a+4)(a﹣5)=2(a2﹣a﹣20)=2×(10﹣20)=﹣20;
(2)∵x2+4x﹣1=0,∴x2+4x=1,
2x4+8x3﹣4x2﹣8x+1=2x2(x2+4x)﹣4x2﹣8x+1=2x2﹣4x2﹣8x+1
=﹣2x2﹣8x+1=﹣2(x2+4x)+1=﹣2+1=﹣1.
24、(1)已知(x+y)2=25,(x﹣y)2=9,求xy和x2+y2的值.
(2)若a2+b2=15,(a﹣b)2=3,求ab和(a+b)2的值.
【分析】(1)首先去括号,进而得出x2+y2的值,即可求出xy的值;
(2)直接利用完全平方公式配方进而得出a,b的值,即可得出答案.
【解答】解:(1)∵(x+y)2=25,(x﹣y)2=9,
∴x2+2xy+y2=25①,x2﹣2xy+y2=9②,
∴①+②得:2(x2+y2)=34,
∴x2+y2=17,
∴17+2xy=25,
∴xy=4;
(2)∵(a﹣b)2=3,
∴a2﹣2ab+b2=3,
∵a2+b2=15,
∴15﹣2ab=3,
∴﹣2ab=﹣12,
∴ab=6,
∵a2+b2=15,
∴a2+2ab+b2=15+12,
∴(a+b)2=27.
25、阅读下列材料:
材料1、将一个形如x2+px+q的二次三项式因式分解时,如果能满足q=mn且p=m+n,则可以把x2+px+q因式分解成(x+m)(x+n)
(1)x2+4x+3=(x+1)(x+3)(2)x2﹣4x﹣12=(x﹣6)(x+2)
材料2、因式分解:(x+y)2+2(x+y)+1
解:将“x+y”看成一个整体,令x+y=A,则原式=A2+2A+1=(A+1)2
再将“A”还原,得:原式=(x+y+1)2
上述解题用到“整体思想”,整体思想是数学解题中常见的一种思想方法,请你解答下列问题:
(1)根据材料1,把x2﹣6x+8分解因式.
(2)结合材料1和材料2,完成下面小题:
①分解因式:(x﹣y)2+4(x﹣y)+3;
②分解因式:m(m+2)(m2+2m﹣2)﹣3.
【分析】(1)利用十字相乘法变形即可得;
(2)①根据材料2的整体思想可以对(x﹣y)2+4(x﹣y)+3分解因式;
②根据材料1和材料2可以对m(m+2)(m2+2m﹣2)﹣3分解因式.
【解答】解:(1)x2﹣6x+8=(x﹣2)(x﹣4);
(2)①令A=x﹣y,
则原式=A2+4A+3=(A+1)(A+3),
所以(x﹣y)2+4(x﹣y)+3=(x﹣y+1)(x﹣y+3);
②令B=m2+2m,则原式=B(B﹣2)﹣3=B2﹣2B﹣3=(B+1)(B﹣3),
所以原式=(m2+2m+1)(m2+2m﹣3)=(m+1)2(m﹣1)(m+3).
26、如图,有足够多的边长为a的小正方形(A类)、长为a宽为b的长方形(B类)以及边长为b的大正方形(C类),发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.
比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)取图①中的若干个(三种图形都要取到)拼成一个长方形,使其面积为(2a+b)(a+2b),在虛框中画出图形,并根据图形回答(2a+b)(a+2b)= ;
(2)若取其中的若干个(三种图形都要取到)拼成一个长方形,使其面积为a2+5ab+6b2.根据你画的长方形,可得到恒等式 ;
(3)如图③,大正方形的边长为m,小正方形的边长为n,若用x,y表示四个相同形状的长方形的两条邻边长(x>y),观察图案,指出以下正确的关系式 (填写选项).
A.xy= B.x+y=m C.x2﹣y2=mn D.x2+y2=
【分析】(1)计算(2a+b)(a+2b)的结果,可知需要A、B、C型的纸片的张数,进而画出拼图;
(2)a2+5ab+6b2即用A型的1张,B型的5张,C型的6张,可以拼图,得出等式;
(3)根据m、n与x、y之间的关系,利用恒等变形,可得结论.
【解答】解:(1)(2a+b)(a+2b)=2a2+5ab+2b2,
故答案为:2a2+5ab+2b2;拼图如图所示:
(2)a2+5ab+6b2即用A型的1张,B型的5张,C型的6张,可以拼成如图所示的图形,
因此可得等式:a2+5ab+6b2=(a+3b)(a+2b),
故答案为:a2+5ab+6b2=(a+3b)(a+2b);
(3)由图③可知,m=x+y,n=x﹣y,因此有m+n=2x,m﹣n=2y,mn=(x+y)(x﹣y)=x2﹣y2;
故答案为:A、B、C、D.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
