广东省深圳市2020-2021学年高一下学期期末模拟考试数学试题(一) Word版含答案
文档属性
| 名称 | 广东省深圳市2020-2021学年高一下学期期末模拟考试数学试题(一) Word版含答案 | 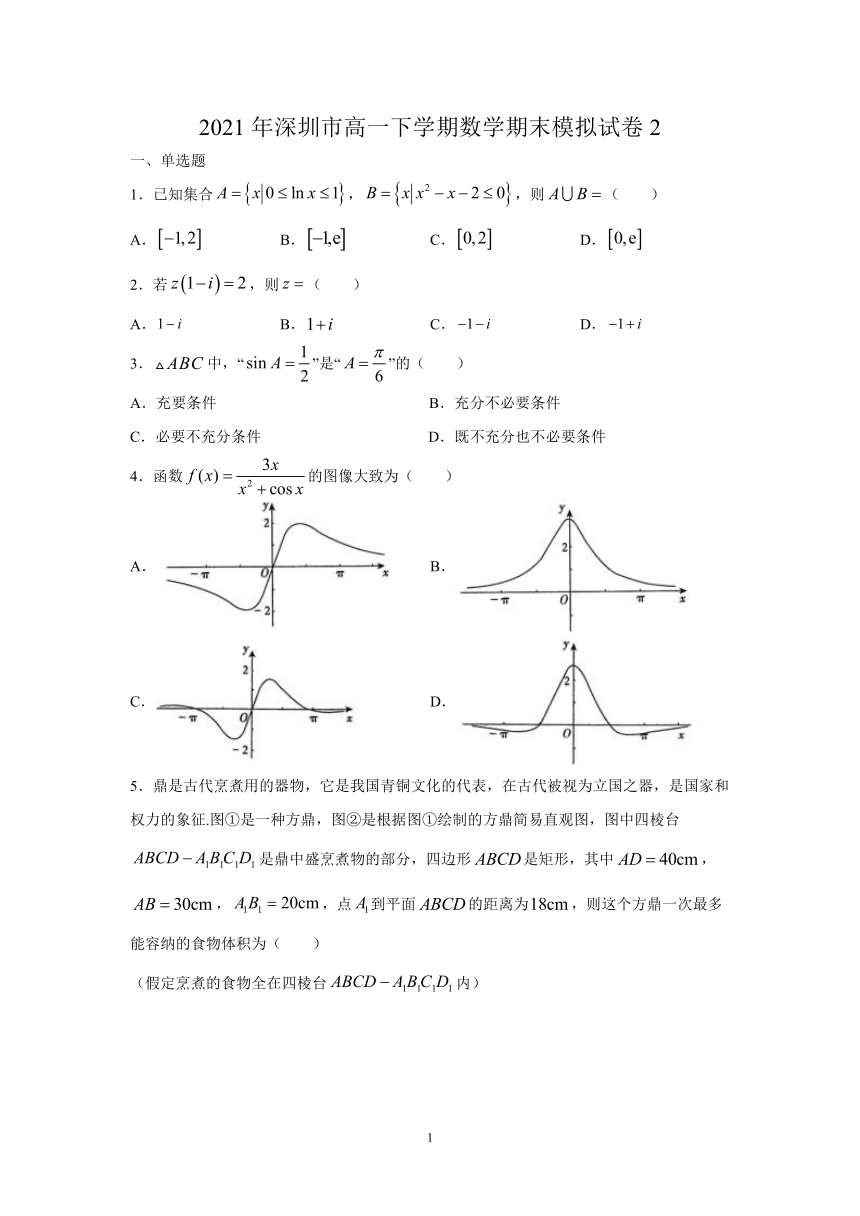 | |
| 格式 | docx | ||
| 文件大小 | 1023.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-10 17:01:21 | ||
图片预览





文档简介
2021年深圳市高一下学期数学期末模拟试卷2
一、单选题
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.若false,则false( )
A.false B.false C.false D.false
3.false中,“false”是“false”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
4.函数false的图像大致为( )
A. B.
C. D.
5.鼎是古代烹煮用的器物,它是我国青铜文化的代表,在古代被视为立国之器,是国家和权力的象征.图①是一种方鼎,图②是根据图①绘制的方鼎简易直观图,图中四棱台false是鼎中盛烹煮物的部分,四边形false是矩形,其中false,false,false,点false到平面false的距离为false,则这个方鼎一次最多能容纳的食物体积为( )
(假定烹煮的食物全在四棱台false内)
A.false B.false C.false D.false
6.设false,false,化简false( )
A.false B.false C.false D.false
36798251181107.“中国天眼”是我国具有自主知识产权,世界最大单口径,最灵敏的球面射电望远镜(如图).其反射面的形状为球冠(球冠是球面被平面所截后剩下的曲面,截得的圆为底,垂直于圆面的直径被截得的部分为高,球冠面积false,其中R为球的半径,h为球冠的高)设球冠底的半径为r,周长为C,球冠的面积为S,则当false时,false( )
false B.false C.false D.false
8.已知定义在false上的奇函数false在false上单调递增,且满足false,则关于false的不等式false的解集为( ).
A.false B.false
C.false D.false
二、多选题
9.日本导演竹内亮拍摄的记录片《后疫情时代》是继《南京抗疫现场》?《好久不见,武汉》之后,又一部以中国抗疫为主题的记录片力作.该片以南京马拉松比赛?无人配送?网络直播等为切入点,真实记录了中国在疫情防控复工复产方面取得的重大成就,并指出:“在新冠疫情冲击下,中国在全球主要经济体中率先恢复增长,成为世界经济体中的亮点”.片中记录某物流公司引进智能无人配送技术,为疫情期间居家隔离网上购物带来了很大的便利,同时也大大提升了公司的效益.2020年全年总收入与2019年全年总收入相比增长了一倍,同时该公司的各项运营成本也随着收入的变化发生了相应变化.下图给出了该公司这两年不同运营成本占全年总成本的比例.已知该公司这两年的年利润率相同,注:年利润率=(全年总收入-全年总成本)/全年总收入.
下列说法错误的是( )
A.该公司2020年原材料费用等于2019年工资金额与研发费用的总和
B.该公司2020年研发费用是2019年工资金额?原材料费用?其他费用三项的总和
C.该公司2020年其他费用占2019年工资金额的false
D.该公司2020年设备费用是2019年原材料费用的两倍
10.已知正数false满足false,则( )
A.false B.false
C.false D.false
11.设P是false所在平面内的一点,false则( )
239395110490A.false B.false
C.false D.false
12.已知正方形false的边长为2,将false沿AC翻折到false的位置,得到四面体false,在翻折过程中,点false始终位于false所在平面的同一侧,且false的最小值为false,则下列结论正确的是( )
A.四面体false的外接球的表面积为false
B.四面体false体积的最大值为false
C.点D的运动轨迹的长度为false
D.边AD旋转所形成的曲面的面积为false
三、填空题
13.已知角false的终边经过点false,若false,则false___________.
14.已知false,点false,false,false,则false的面积的取值范围是______________.
15.已知平面非零向量false两两所成的角相等,false,则false的值为_____.
四、解答题
17.已知复数z=+(a2-5a-6)i(a∈R),试求实数a取什么值时,z分别为
(1)实数;(2)虚数;(3)纯虚数.
18.在△ABC中,D是BC的中点,AB=2,AC=3,AD=2。
(1)求△ABC的面积;
(2)若E为BC上一点,且false,求λ的值。
19.有一种鱼的身体吸收汞,当这种鱼身体中的汞含量超过其体重的false(即百万分之一)时,人食用它,就会对人体产生危害.现从一批该鱼中随机选出false条鱼,检验鱼体中的汞含量与其体重的比值(单位:false),数据统计如下:
false
(1)求上述数据的中位数、众数、极差,并估计这批鱼该项数据的false分位数;
(2)有false,false两个水池,两水池之间有false个完全相同的小孔联通,所有的小孔均在水下,且可以同时通过false条鱼.
(ⅰ)将其中汞的含量最低的false条鱼分别放入false水池和false水池中,若这false条鱼的游动相互独立,均有false的概率进入另一水池且不再游回,求这两条鱼最终在同一水池的概率;
(ⅱ)将其中汞的含量最低的false条鱼都先放入false水池中,若这false条鱼均会独立地且等可能地从其中任意一个小孔由false水池进入false水池且不再游回false水池,求这两条鱼由不同小孔进入false水池的概率.
20.(本小题满分12分)
某市一湿地公园建设项目中,拟在如图所示一片水域打造一个浅水滩,并在false、false、false、false四个位置建四座观景台,在凸四边形false中,false千米.false千米.
(1)用false表示false;
(2)现要在false、false两处连接一根水下直管道,已知false,问最少应准备多少千米管道(结果可用根式表示).
21.如图,已知等腰梯形false中,false,false,false,false于点false,现将△false沿false翻折到△false的位置,使得二面角false的大小为120°,若点false为false的三等分点,且false.
(1)求证:false平面false;
(2)求平面false和平面false所成锐二面角的余弦值.
22.已知函数false.
(1)当false时,解不等式false;
(2)若关于false的方程false在区间false上恰有一个实数解,求false的取值范围;
(3)设false,若存在false使得函数false在区间false上的最大值和最小值的差不超过1,求false的取值范围.
一、单选题
1.已知集合false,false,则false( )
A.false B.false C.false D.false
【答案】B
2.若false,则false( )
A.false B.false C.false D.false
【答案】B
3.false中,“false”是“false”的( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件
【答案】C
4.函数false的图像大致为( )
A. B.
C. D.
【答案】A
【详解】
因为false,
所以false为奇函数,其图象关于原点对称,排除B,D;
因为false,所以排除C,
故选:A.
5.鼎是古代烹煮用的器物,它是我国青铜文化的代表,在古代被视为立国之器,是国家和权力的象征.图①是一种方鼎,图②是根据图①绘制的方鼎简易直观图,图中四棱台false是鼎中盛烹煮物的部分,四边形false是矩形,其中false,false,false,点false到平面false的距离为false,则这个方鼎一次最多能容纳的食物体积为( )
(假定烹煮的食物全在四棱台false内)
A.false B.false C.false D.false
【答案】D
【详解】
几何体false为四棱台,所以延长false必交于一点,记为O,
且四棱锥false相似于false,所以false.过点false作OH⊥面false于H,
作OG⊥面false于G,则false,又false,解得:OG=false,OH=false,
四棱台false的体积false.
故选:D
6.设false,false,化简false( )
A.false B.false C.false D.false
【答案】A
【详解】
因为false,false,
所以false,
false,
false,
false,
false,
false,
故选:A
7.B
false,false,
false,又false,false ,
false,解得:false,即false,false
故选:B
8.C
false为false上的奇函数,false,
令false,则false,
false为false上奇函数;
false在false上单调递增,false在false上单调递增,
false在false上单调递增,由奇函数性质知:false在false上单调递增;
false,false,则false,
又false,当false时,false,
false当false时,false不成立,即false不成立,
由此可在坐标系中画出false与false大致图象如下图所示:
由图象可知:当false时,false,
即当false时,false. 故选:C.
二、多选题
9.日本导演竹内亮拍摄的记录片《后疫情时代》是继《南京抗疫现场》?《好久不见,武汉》之后,又一部以中国抗疫为主题的记录片力作.该片以南京马拉松比赛?无人配送?网络直播等为切入点,真实记录了中国在疫情防控复工复产方面取得的重大成就,并指出:“在新冠疫情冲击下,中国在全球主要经济体中率先恢复增长,成为世界经济体中的亮点”.片中记录某物流公司引进智能无人配送技术,为疫情期间居家隔离网上购物带来了很大的便利,同时也大大提升了公司的效益.2020年全年总收入与2019年全年总收入相比增长了一倍,同时该公司的各项运营成本也随着收入的变化发生了相应变化.下图给出了该公司这两年不同运营成本占全年总成本的比例.已知该公司这两年的年利润率相同,注:年利润率=(全年总收入-全年总成本)/全年总收入.
下列说法错误的是( )
A.该公司2020年原材料费用等于2019年工资金额与研发费用的总和
B.该公司2020年研发费用是2019年工资金额?原材料费用?其他费用三项的总和
C.该公司2020年其他费用占2019年工资金额的false
D.该公司2020年设备费用是2019年原材料费用的两倍
【答案】ACD
【详解】
不妨设2019年全年的总成本为false,则2020年全年的总成本为false.
该公司2020年原材料费用为false,2019年工资金额与研发费用的和为false,故A错误;
该公司2020年研发费用为false,2019年工资金额?原材料费用?其他费用三项的和为false,故B正确;
该公司2020年其他费用为false,2019年工资金额为false,故C错误;
该公司2020年设备费用为false,2019年原材料费用为false,故D错误,
故选:ACD
10.已知正数false满足false,则( )
A.false B.false
C.false D.false
【答案】ACD
【详解】
A:由false,又false,得false,所以false,正确;
B:由false,当false时有false,此时false,错误;
C:由false,所以false,正确;
D:由false,所以false,正确.
故选:false
CD
12.已知正方形false的边长为2,将false沿AC翻折到false的位置,得到四面体false,在翻折过程中,点false始终位于false所在平面的同一侧,且false的最小值为false,则下列结论正确的是( )
A.四面体false的外接球的表面积为false
B.四面体false体积的最大值为false
C.点D的运动轨迹的长度为false
D.边AD旋转所形成的曲面的面积为false
【答案】ACD
【详解】
解:对A:false,
falseAC中点即为四面体false的外接球的球心,AC为球的直径,
falsefalse,
false,故选项A正确;
对B:当平面falsefalse平面false时,四面体false体积的最大,此时高为false,
false,故选项B错误;
对C:设方形false对角线AC与BD交于O,
由题意,翻折后当false的最小值为false时,false为边长为false的等边三角形,
此时false,所以点D的运动轨迹是以O为圆心false为半径的圆心角为false的圆弧,
所以点D的运动轨迹的长度为false,故选项C正确;
对D:结合C的分析知,边AD旋转所形成的曲面的面积为以A为顶点,
底面圆为以O为圆心false为半径的圆锥的侧面积的false,
即所求曲面的面积为false,故选项D正确.
故选: ACD.
三、填空题
13.false
【详解】由题意,角false的终边经过点false,可得false.
又由false,得false,
根据三角函数的定义,可得false,解得false. 故答案为:false.
14.取AC的中点E,将△ABC面积分成左右两边求解
17.【解析】(1)当z为实数时,则a2-5a-6=0,且有意义,
∴a=-1,或a=6,且a≠±1,
∴当a=6时,z为实数.
(2)当z为虚数时,则a2-5a-6≠0,且有意义,
∴a≠-1,且a≠6,且a≠±1.
∴当a≠±1,且a≠6时,z为虚数,
即当a∈(-∞,-1)∪(-1,1)∪(1,6)∪(6,+∞)时,z为虚数.
(3)当z为纯虚数时,则有a2-5a-6≠0,
且=0.
∴
∴不存在实数a使z为纯虚数.
18.解析
19.19.
解:(1)由题意知,数据的中位数为false
数据的众数为false
数据的极差为false
估计这批鱼该项数据的false百分位数约为false
(2)(ⅰ)记“两鱼最终均在false水池”为事件false,则false
记“两鱼最终均在false水池”为事件false,则false
∵事件false与事件false互斥,
∴两条鱼最终在同一水池的概率为false
(ⅱ)记“两鱼同时从第一个小孔通过”为事件false,“两鱼同时从第二个小孔通过”为
事件false,false依次类推;而两鱼的游动独立
∴false
记“两条鱼由不同小孔进入false水池”为事件false,则false与false对立,又由事件false,事件false,false互斥
∴false
即false
20.【解析】(1)连结false.
在false中,false.
在false中,false,
故有false,从而false.
(2)因为false,所以由(1)可得false,
false,所以false,而false,故false.
此时false.
从而false,所以false为等腰三角形.
false,false,
false.
所以false
false.
从而false千米
21.【详解】(1)取false的三等分点false且false,连接false,false,
∵false,∴false且false.
在等腰梯形false中,false,false,false,false,
∴false且false,
∴false且false,即四边形false为平行四边形,
∴false,又false平面false,false平面false,
∴false平面false.
(2)过false作false,则false,过false作false于false,连接false,则false,
∴false为面false和面false所成锐二面角的平面角.
在false中,false,false,false,
∴false,即面false和面false所成锐二面角的余弦值为false.
22.解析
一、单选题
1.已知集合false,false,则false( )
A.false B.false C.false D.false
2.若false,则false( )
A.false B.false C.false D.false
3.false中,“false”是“false”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
4.函数false的图像大致为( )
A. B.
C. D.
5.鼎是古代烹煮用的器物,它是我国青铜文化的代表,在古代被视为立国之器,是国家和权力的象征.图①是一种方鼎,图②是根据图①绘制的方鼎简易直观图,图中四棱台false是鼎中盛烹煮物的部分,四边形false是矩形,其中false,false,false,点false到平面false的距离为false,则这个方鼎一次最多能容纳的食物体积为( )
(假定烹煮的食物全在四棱台false内)
A.false B.false C.false D.false
6.设false,false,化简false( )
A.false B.false C.false D.false
36798251181107.“中国天眼”是我国具有自主知识产权,世界最大单口径,最灵敏的球面射电望远镜(如图).其反射面的形状为球冠(球冠是球面被平面所截后剩下的曲面,截得的圆为底,垂直于圆面的直径被截得的部分为高,球冠面积false,其中R为球的半径,h为球冠的高)设球冠底的半径为r,周长为C,球冠的面积为S,则当false时,false( )
false B.false C.false D.false
8.已知定义在false上的奇函数false在false上单调递增,且满足false,则关于false的不等式false的解集为( ).
A.false B.false
C.false D.false
二、多选题
9.日本导演竹内亮拍摄的记录片《后疫情时代》是继《南京抗疫现场》?《好久不见,武汉》之后,又一部以中国抗疫为主题的记录片力作.该片以南京马拉松比赛?无人配送?网络直播等为切入点,真实记录了中国在疫情防控复工复产方面取得的重大成就,并指出:“在新冠疫情冲击下,中国在全球主要经济体中率先恢复增长,成为世界经济体中的亮点”.片中记录某物流公司引进智能无人配送技术,为疫情期间居家隔离网上购物带来了很大的便利,同时也大大提升了公司的效益.2020年全年总收入与2019年全年总收入相比增长了一倍,同时该公司的各项运营成本也随着收入的变化发生了相应变化.下图给出了该公司这两年不同运营成本占全年总成本的比例.已知该公司这两年的年利润率相同,注:年利润率=(全年总收入-全年总成本)/全年总收入.
下列说法错误的是( )
A.该公司2020年原材料费用等于2019年工资金额与研发费用的总和
B.该公司2020年研发费用是2019年工资金额?原材料费用?其他费用三项的总和
C.该公司2020年其他费用占2019年工资金额的false
D.该公司2020年设备费用是2019年原材料费用的两倍
10.已知正数false满足false,则( )
A.false B.false
C.false D.false
11.设P是false所在平面内的一点,false则( )
239395110490A.false B.false
C.false D.false
12.已知正方形false的边长为2,将false沿AC翻折到false的位置,得到四面体false,在翻折过程中,点false始终位于false所在平面的同一侧,且false的最小值为false,则下列结论正确的是( )
A.四面体false的外接球的表面积为false
B.四面体false体积的最大值为false
C.点D的运动轨迹的长度为false
D.边AD旋转所形成的曲面的面积为false
三、填空题
13.已知角false的终边经过点false,若false,则false___________.
14.已知false,点false,false,false,则false的面积的取值范围是______________.
15.已知平面非零向量false两两所成的角相等,false,则false的值为_____.
四、解答题
17.已知复数z=+(a2-5a-6)i(a∈R),试求实数a取什么值时,z分别为
(1)实数;(2)虚数;(3)纯虚数.
18.在△ABC中,D是BC的中点,AB=2,AC=3,AD=2。
(1)求△ABC的面积;
(2)若E为BC上一点,且false,求λ的值。
19.有一种鱼的身体吸收汞,当这种鱼身体中的汞含量超过其体重的false(即百万分之一)时,人食用它,就会对人体产生危害.现从一批该鱼中随机选出false条鱼,检验鱼体中的汞含量与其体重的比值(单位:false),数据统计如下:
false
(1)求上述数据的中位数、众数、极差,并估计这批鱼该项数据的false分位数;
(2)有false,false两个水池,两水池之间有false个完全相同的小孔联通,所有的小孔均在水下,且可以同时通过false条鱼.
(ⅰ)将其中汞的含量最低的false条鱼分别放入false水池和false水池中,若这false条鱼的游动相互独立,均有false的概率进入另一水池且不再游回,求这两条鱼最终在同一水池的概率;
(ⅱ)将其中汞的含量最低的false条鱼都先放入false水池中,若这false条鱼均会独立地且等可能地从其中任意一个小孔由false水池进入false水池且不再游回false水池,求这两条鱼由不同小孔进入false水池的概率.
20.(本小题满分12分)
某市一湿地公园建设项目中,拟在如图所示一片水域打造一个浅水滩,并在false、false、false、false四个位置建四座观景台,在凸四边形false中,false千米.false千米.
(1)用false表示false;
(2)现要在false、false两处连接一根水下直管道,已知false,问最少应准备多少千米管道(结果可用根式表示).
21.如图,已知等腰梯形false中,false,false,false,false于点false,现将△false沿false翻折到△false的位置,使得二面角false的大小为120°,若点false为false的三等分点,且false.
(1)求证:false平面false;
(2)求平面false和平面false所成锐二面角的余弦值.
22.已知函数false.
(1)当false时,解不等式false;
(2)若关于false的方程false在区间false上恰有一个实数解,求false的取值范围;
(3)设false,若存在false使得函数false在区间false上的最大值和最小值的差不超过1,求false的取值范围.
一、单选题
1.已知集合false,false,则false( )
A.false B.false C.false D.false
【答案】B
2.若false,则false( )
A.false B.false C.false D.false
【答案】B
3.false中,“false”是“false”的( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件
【答案】C
4.函数false的图像大致为( )
A. B.
C. D.
【答案】A
【详解】
因为false,
所以false为奇函数,其图象关于原点对称,排除B,D;
因为false,所以排除C,
故选:A.
5.鼎是古代烹煮用的器物,它是我国青铜文化的代表,在古代被视为立国之器,是国家和权力的象征.图①是一种方鼎,图②是根据图①绘制的方鼎简易直观图,图中四棱台false是鼎中盛烹煮物的部分,四边形false是矩形,其中false,false,false,点false到平面false的距离为false,则这个方鼎一次最多能容纳的食物体积为( )
(假定烹煮的食物全在四棱台false内)
A.false B.false C.false D.false
【答案】D
【详解】
几何体false为四棱台,所以延长false必交于一点,记为O,
且四棱锥false相似于false,所以false.过点false作OH⊥面false于H,
作OG⊥面false于G,则false,又false,解得:OG=false,OH=false,
四棱台false的体积false.
故选:D
6.设false,false,化简false( )
A.false B.false C.false D.false
【答案】A
【详解】
因为false,false,
所以false,
false,
false,
false,
false,
false,
故选:A
7.B
false,false,
false,又false,false ,
false,解得:false,即false,false
故选:B
8.C
false为false上的奇函数,false,
令false,则false,
false为false上奇函数;
false在false上单调递增,false在false上单调递增,
false在false上单调递增,由奇函数性质知:false在false上单调递增;
false,false,则false,
又false,当false时,false,
false当false时,false不成立,即false不成立,
由此可在坐标系中画出false与false大致图象如下图所示:
由图象可知:当false时,false,
即当false时,false. 故选:C.
二、多选题
9.日本导演竹内亮拍摄的记录片《后疫情时代》是继《南京抗疫现场》?《好久不见,武汉》之后,又一部以中国抗疫为主题的记录片力作.该片以南京马拉松比赛?无人配送?网络直播等为切入点,真实记录了中国在疫情防控复工复产方面取得的重大成就,并指出:“在新冠疫情冲击下,中国在全球主要经济体中率先恢复增长,成为世界经济体中的亮点”.片中记录某物流公司引进智能无人配送技术,为疫情期间居家隔离网上购物带来了很大的便利,同时也大大提升了公司的效益.2020年全年总收入与2019年全年总收入相比增长了一倍,同时该公司的各项运营成本也随着收入的变化发生了相应变化.下图给出了该公司这两年不同运营成本占全年总成本的比例.已知该公司这两年的年利润率相同,注:年利润率=(全年总收入-全年总成本)/全年总收入.
下列说法错误的是( )
A.该公司2020年原材料费用等于2019年工资金额与研发费用的总和
B.该公司2020年研发费用是2019年工资金额?原材料费用?其他费用三项的总和
C.该公司2020年其他费用占2019年工资金额的false
D.该公司2020年设备费用是2019年原材料费用的两倍
【答案】ACD
【详解】
不妨设2019年全年的总成本为false,则2020年全年的总成本为false.
该公司2020年原材料费用为false,2019年工资金额与研发费用的和为false,故A错误;
该公司2020年研发费用为false,2019年工资金额?原材料费用?其他费用三项的和为false,故B正确;
该公司2020年其他费用为false,2019年工资金额为false,故C错误;
该公司2020年设备费用为false,2019年原材料费用为false,故D错误,
故选:ACD
10.已知正数false满足false,则( )
A.false B.false
C.false D.false
【答案】ACD
【详解】
A:由false,又false,得false,所以false,正确;
B:由false,当false时有false,此时false,错误;
C:由false,所以false,正确;
D:由false,所以false,正确.
故选:false
CD
12.已知正方形false的边长为2,将false沿AC翻折到false的位置,得到四面体false,在翻折过程中,点false始终位于false所在平面的同一侧,且false的最小值为false,则下列结论正确的是( )
A.四面体false的外接球的表面积为false
B.四面体false体积的最大值为false
C.点D的运动轨迹的长度为false
D.边AD旋转所形成的曲面的面积为false
【答案】ACD
【详解】
解:对A:false,
falseAC中点即为四面体false的外接球的球心,AC为球的直径,
falsefalse,
false,故选项A正确;
对B:当平面falsefalse平面false时,四面体false体积的最大,此时高为false,
false,故选项B错误;
对C:设方形false对角线AC与BD交于O,
由题意,翻折后当false的最小值为false时,false为边长为false的等边三角形,
此时false,所以点D的运动轨迹是以O为圆心false为半径的圆心角为false的圆弧,
所以点D的运动轨迹的长度为false,故选项C正确;
对D:结合C的分析知,边AD旋转所形成的曲面的面积为以A为顶点,
底面圆为以O为圆心false为半径的圆锥的侧面积的false,
即所求曲面的面积为false,故选项D正确.
故选: ACD.
三、填空题
13.false
【详解】由题意,角false的终边经过点false,可得false.
又由false,得false,
根据三角函数的定义,可得false,解得false. 故答案为:false.
14.取AC的中点E,将△ABC面积分成左右两边求解
17.【解析】(1)当z为实数时,则a2-5a-6=0,且有意义,
∴a=-1,或a=6,且a≠±1,
∴当a=6时,z为实数.
(2)当z为虚数时,则a2-5a-6≠0,且有意义,
∴a≠-1,且a≠6,且a≠±1.
∴当a≠±1,且a≠6时,z为虚数,
即当a∈(-∞,-1)∪(-1,1)∪(1,6)∪(6,+∞)时,z为虚数.
(3)当z为纯虚数时,则有a2-5a-6≠0,
且=0.
∴
∴不存在实数a使z为纯虚数.
18.解析
19.19.
解:(1)由题意知,数据的中位数为false
数据的众数为false
数据的极差为false
估计这批鱼该项数据的false百分位数约为false
(2)(ⅰ)记“两鱼最终均在false水池”为事件false,则false
记“两鱼最终均在false水池”为事件false,则false
∵事件false与事件false互斥,
∴两条鱼最终在同一水池的概率为false
(ⅱ)记“两鱼同时从第一个小孔通过”为事件false,“两鱼同时从第二个小孔通过”为
事件false,false依次类推;而两鱼的游动独立
∴false
记“两条鱼由不同小孔进入false水池”为事件false,则false与false对立,又由事件false,事件false,false互斥
∴false
即false
20.【解析】(1)连结false.
在false中,false.
在false中,false,
故有false,从而false.
(2)因为false,所以由(1)可得false,
false,所以false,而false,故false.
此时false.
从而false,所以false为等腰三角形.
false,false,
false.
所以false
false.
从而false千米
21.【详解】(1)取false的三等分点false且false,连接false,false,
∵false,∴false且false.
在等腰梯形false中,false,false,false,false,
∴false且false,
∴false且false,即四边形false为平行四边形,
∴false,又false平面false,false平面false,
∴false平面false.
(2)过false作false,则false,过false作false于false,连接false,则false,
∴false为面false和面false所成锐二面角的平面角.
在false中,false,false,false,
∴false,即面false和面false所成锐二面角的余弦值为false.
22.解析
同课章节目录
