苏科版七年级数学上册课件 3.1 用字母表示数(共20张ppt)
文档属性
| 名称 | 苏科版七年级数学上册课件 3.1 用字母表示数(共20张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 17:16:52 | ||
图片预览



文档简介
(共20张PPT)
3.1 字母表示数
第三章 代数式
在生活中,经常用图标表示某种意义。
a
h
= ah
1
2
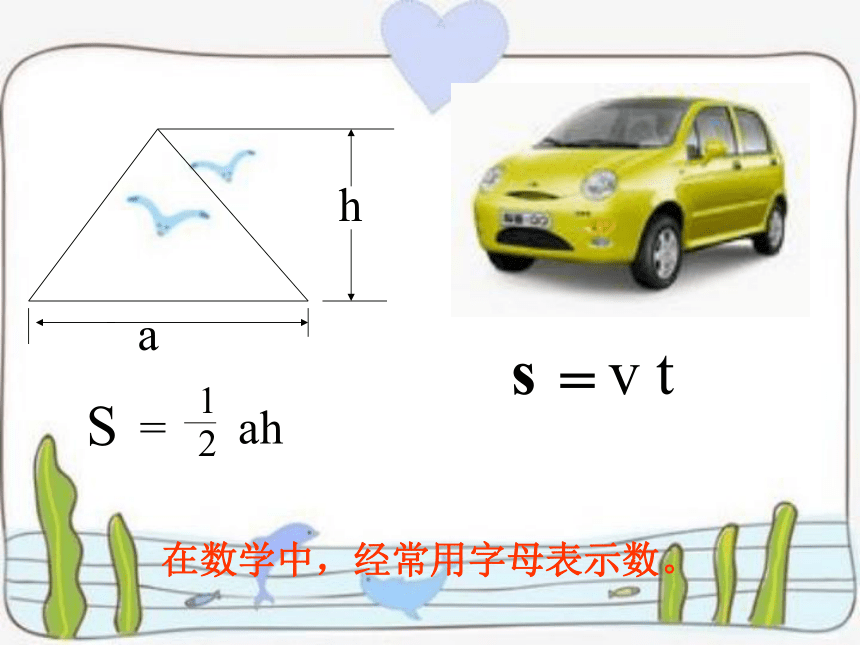
在数学中,经常用字母表示数。
v t
S
s
=
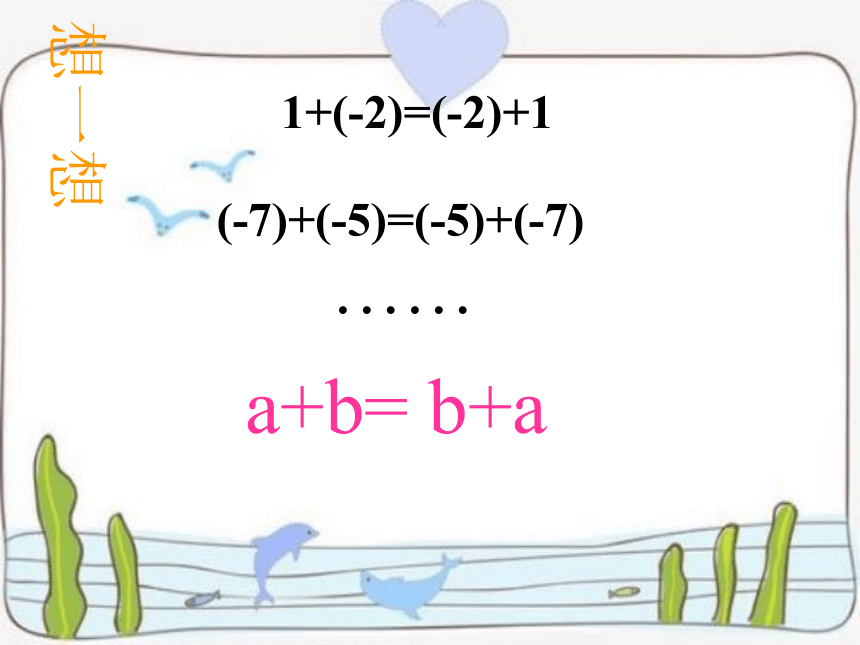
1+(-2)=(-2)+1
(-7)+(-5)=(-5)+(-7)
……
a+b= b+a
想一想
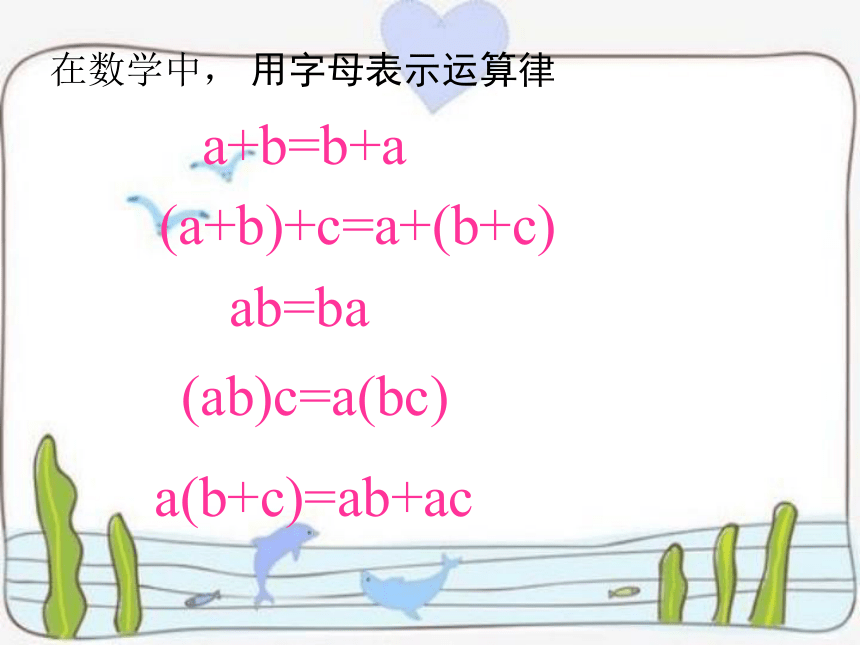
在数学中, 用字母表示运算律
a+b=b+a
(a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
a(b+c)=ab+ac
完成书本第67页试一试
友情提示:
①乘法:数与字母、字母与字母中间的乘号通常可以省略不写,或用“·”表示。
省略乘号时,应把数写在字母的前面;
②除法:除号写成分数形式;
③乘方:相同因式的乘积写成幂的形式
④分数:带分数写成假分数
⑤单位:最后一步运算为加减的式子,若后面有单位,要用括号把整个式子括起来。
√
√
×
√
×
×
×
×
×
×
×
√
√
书写正确吗?
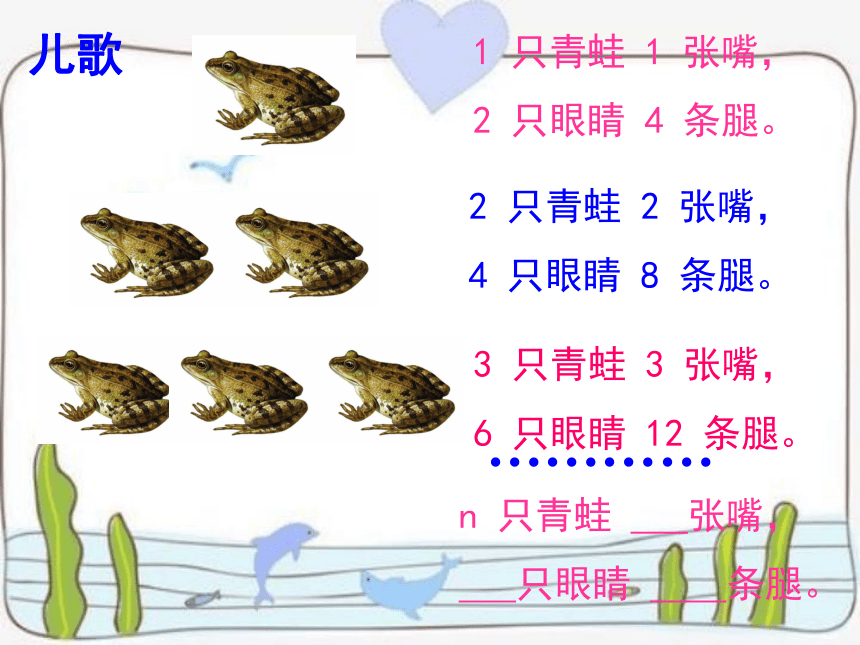
儿歌
1 只青蛙 1 张嘴,
2 只眼睛 4 条腿。
2 只青蛙 2 张嘴,
4 只眼睛 8 条腿。
3 只青蛙 3 张嘴,
6 只眼睛 12 条腿。
…………
n 只青蛙 张嘴,
只眼睛 条腿。
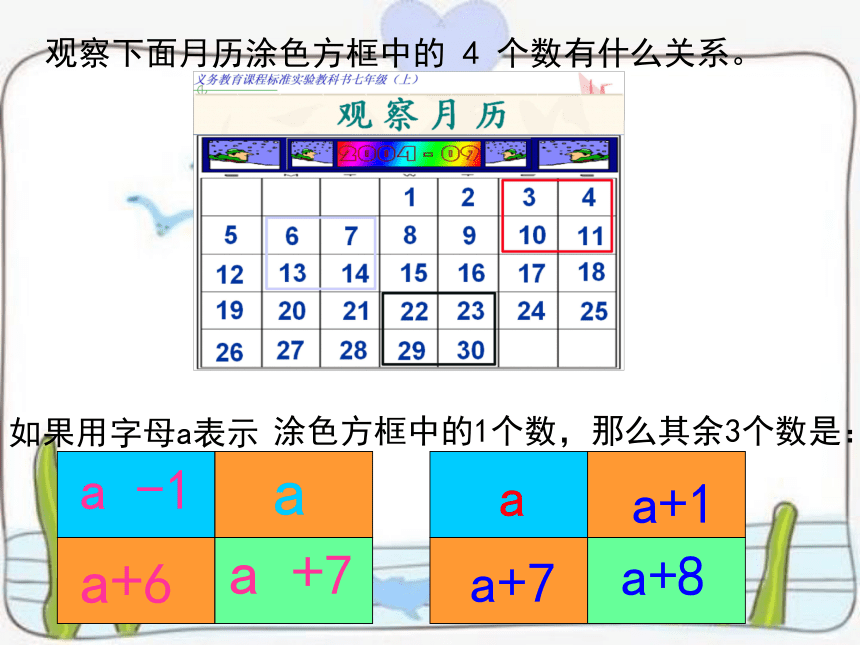
观察下面月历涂色方框中的 4 个数有什么关系。
如果用字母a表示
涂色方框中的1个数,那么其余3个数是:
a
a -1
a+6
a +7
a
a+1
a+7
a+8
搭1个正方形需要4根火柴棒.
(2)搭5个正方形需要 根火柴棒;
(3)搭50个正方形需要 根火柴棒;
(4)搭n个正方形需要 根火柴棒;
(5)利用你的计算方法,搭2004个这样的正方形需要 根火柴棒?
按如图所示方式搭图形
(1)搭2个正方形需要 根火柴棒;搭3个正方形需要 根火柴棒;
数学实验室
第①个图形中有 1 个小正方形。
第③个图形比第②个图形多 个小正方形。
第④个图形比第③个图形多 个小正方形。
(2)第100个图形比第99 个图形多几个小正方形?
100
99
3
5
7
(3)第 个图形比第 个图形多几个小正方形?
n
n-1
(1)第⑩个图形比第⑨个图形多几个小正方形?
第②个图形比第①个图形多 个小正方形。
①
②
③
④
①
②
③
…
④
. . . . . . . .
. . . . . . .
n
n列
n行
…
第n个图形比第(n-1)个多 个小正方形。
[ n+(n-1) ]
图②比图①多(2+1)个小正方形
图③比图②
多(3+2)
个小正方形
图④比图①
多(4+3)
个小正方形
①
②
③
…
④
. . . . . . . .
. . . . . . .
n
n列
n行
第n个图形比第(n-1)个多 个小正方形。
( n+n-1)
图②比图①
多(2+2-1)
个小正方形
图③比图②
多(3+3-1)
个小正方形
图④比图①
多(4+4-1)
个小正方形
①
②
③
…
④
①
. . . . . . . .
. . . . . . .
n
n列
n行
第n个图形比第(n-1)个多 个小正方形。
[1+(n-1)+(n-1)]
图②比图①
多(1+1+1)
个小正方形
图③比图②
多(1+2+2)
个小正方形
图④比图①
多(1+3+3)
个小正方形
第n个图形比第(n-1)个多 个小正方形。
第n个图形比第(n-1)个多 个小正方形。
第n个图形比第(n-1)个多 个小正方形。
第n个图形比第(n-1)个多 个小正方形。
[ n+(n-1) ]
( n+n-1)
[1+(n-1)+(n-1)]
[ n -(n-1) ]
2
2
1、某城市市区人口a万人,市区绿化面积 b 万㎡,则平均每个人拥有绿地____㎡。
2 、某城市 5 年前人均年收入为 n 元,预计今年人均年收入是 5 年前的 2 倍多 500 元,那么今年人均年收入将达 元。
3 、如图,这个长方体的体积是______,表面积是 。
b
a
(2 n+500)
abc
2(ab+bc+ ac)
练一练
4 、图中的阴影部分的面积是______,周长是______。
2 π r
πr
1
2
2
a
b
a
b
(1)正方形①的面积为
(2)长方形②的面积为
(3)长方形③的面积为
(4)正方形④的面积为
(5)因此大正方形的面积为
(6)大正方形的边长是
(7)它的面积为
从中发现等量关系了吗?
1
2
3
4
5、
练习:
书本第68页
回忆一下:
这节课你学到了什么?有什么收获?
3.1 字母表示数
第三章 代数式
在生活中,经常用图标表示某种意义。
a
h
= ah
1
2
在数学中,经常用字母表示数。
v t
S
s
=
1+(-2)=(-2)+1
(-7)+(-5)=(-5)+(-7)
……
a+b= b+a
想一想
在数学中, 用字母表示运算律
a+b=b+a
(a+b)+c=a+(b+c)
ab=ba
(ab)c=a(bc)
a(b+c)=ab+ac
完成书本第67页试一试
友情提示:
①乘法:数与字母、字母与字母中间的乘号通常可以省略不写,或用“·”表示。
省略乘号时,应把数写在字母的前面;
②除法:除号写成分数形式;
③乘方:相同因式的乘积写成幂的形式
④分数:带分数写成假分数
⑤单位:最后一步运算为加减的式子,若后面有单位,要用括号把整个式子括起来。
√
√
×
√
×
×
×
×
×
×
×
√
√
书写正确吗?
儿歌
1 只青蛙 1 张嘴,
2 只眼睛 4 条腿。
2 只青蛙 2 张嘴,
4 只眼睛 8 条腿。
3 只青蛙 3 张嘴,
6 只眼睛 12 条腿。
…………
n 只青蛙 张嘴,
只眼睛 条腿。
观察下面月历涂色方框中的 4 个数有什么关系。
如果用字母a表示
涂色方框中的1个数,那么其余3个数是:
a
a -1
a+6
a +7
a
a+1
a+7
a+8
搭1个正方形需要4根火柴棒.
(2)搭5个正方形需要 根火柴棒;
(3)搭50个正方形需要 根火柴棒;
(4)搭n个正方形需要 根火柴棒;
(5)利用你的计算方法,搭2004个这样的正方形需要 根火柴棒?
按如图所示方式搭图形
(1)搭2个正方形需要 根火柴棒;搭3个正方形需要 根火柴棒;
数学实验室
第①个图形中有 1 个小正方形。
第③个图形比第②个图形多 个小正方形。
第④个图形比第③个图形多 个小正方形。
(2)第100个图形比第99 个图形多几个小正方形?
100
99
3
5
7
(3)第 个图形比第 个图形多几个小正方形?
n
n-1
(1)第⑩个图形比第⑨个图形多几个小正方形?
第②个图形比第①个图形多 个小正方形。
①
②
③
④
①
②
③
…
④
. . . . . . . .
. . . . . . .
n
n列
n行
…
第n个图形比第(n-1)个多 个小正方形。
[ n+(n-1) ]
图②比图①多(2+1)个小正方形
图③比图②
多(3+2)
个小正方形
图④比图①
多(4+3)
个小正方形
①
②
③
…
④
. . . . . . . .
. . . . . . .
n
n列
n行
第n个图形比第(n-1)个多 个小正方形。
( n+n-1)
图②比图①
多(2+2-1)
个小正方形
图③比图②
多(3+3-1)
个小正方形
图④比图①
多(4+4-1)
个小正方形
①
②
③
…
④
①
. . . . . . . .
. . . . . . .
n
n列
n行
第n个图形比第(n-1)个多 个小正方形。
[1+(n-1)+(n-1)]
图②比图①
多(1+1+1)
个小正方形
图③比图②
多(1+2+2)
个小正方形
图④比图①
多(1+3+3)
个小正方形
第n个图形比第(n-1)个多 个小正方形。
第n个图形比第(n-1)个多 个小正方形。
第n个图形比第(n-1)个多 个小正方形。
第n个图形比第(n-1)个多 个小正方形。
[ n+(n-1) ]
( n+n-1)
[1+(n-1)+(n-1)]
[ n -(n-1) ]
2
2
1、某城市市区人口a万人,市区绿化面积 b 万㎡,则平均每个人拥有绿地____㎡。
2 、某城市 5 年前人均年收入为 n 元,预计今年人均年收入是 5 年前的 2 倍多 500 元,那么今年人均年收入将达 元。
3 、如图,这个长方体的体积是______,表面积是 。
b
a
(2 n+500)
abc
2(ab+bc+ ac)
练一练
4 、图中的阴影部分的面积是______,周长是______。
2 π r
πr
1
2
2
a
b
a
b
(1)正方形①的面积为
(2)长方形②的面积为
(3)长方形③的面积为
(4)正方形④的面积为
(5)因此大正方形的面积为
(6)大正方形的边长是
(7)它的面积为
从中发现等量关系了吗?
1
2
3
4
5、
练习:
书本第68页
回忆一下:
这节课你学到了什么?有什么收获?
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
