苏科版七年级数学上册课件 5.2图形的运动(共30张ppt)
文档属性
| 名称 | 苏科版七年级数学上册课件 5.2图形的运动(共30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
我们生活的这个世界处在不停的运动和变化之中,人们不停地在研究这些运动和变化,并寻找规律……
5.2 图形的运动
观察下面的图片,你发现了什么?
点动成线
线动成面
O
A
B
A
交流与发现
你还能举出生活中“点动成线,线动成面”的例子吗
想一想
点动成线
感受点的运动
线 成面
动
动
感受线的运动
线
成面
动
感受线的运动
【探索活动一】
1.长方形纸板绕它的一条边旋转1周;
2.直角三角尺绕它的一条直角边旋转1周;
3.一枚硬币在桌面上竖直快速旋转.
它们分别形成怎样的几何体?
请同学们分小组讨论一下,说说你的猜想?
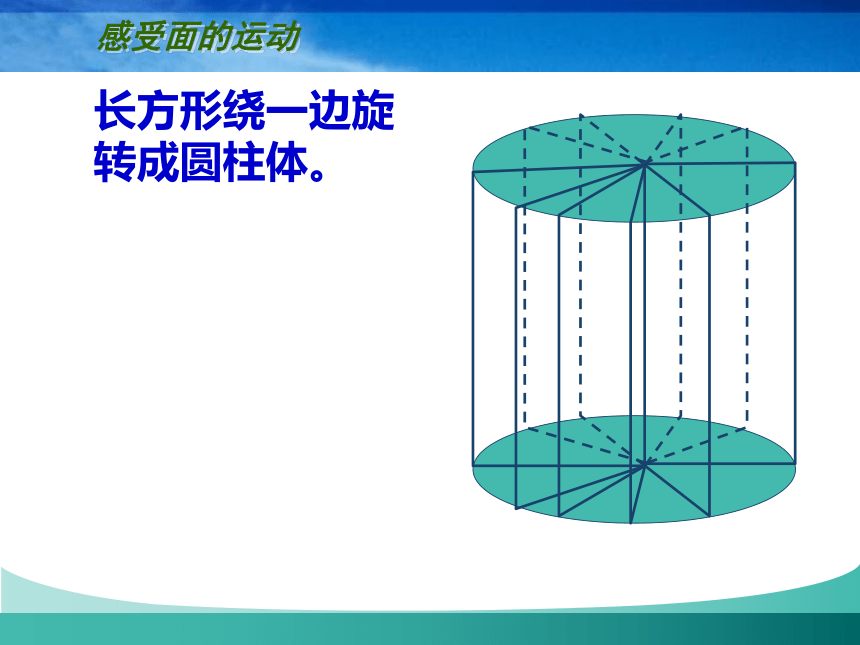
长方形绕一边旋转成圆柱体。
感受面的运动
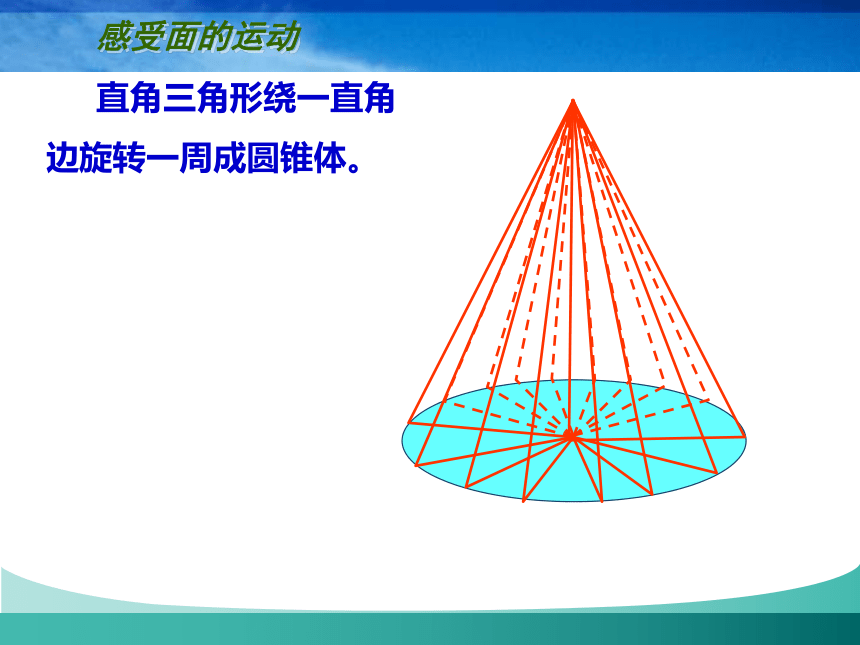
直角三角形绕一直角
边旋转一周成圆锥体。
感受面的运动
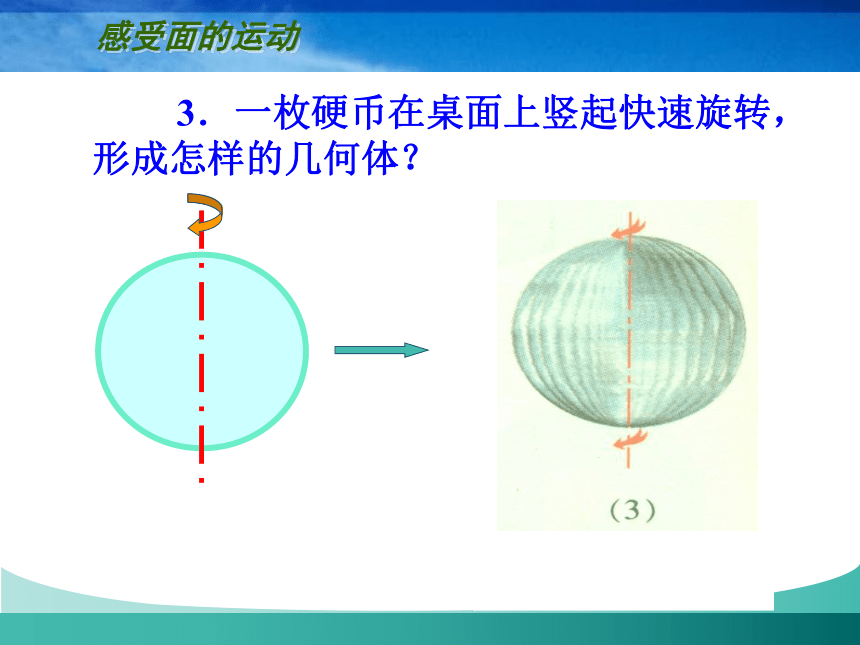
3.一枚硬币在桌面上竖起快速旋转,形成怎样的几何体?
感受面的运动
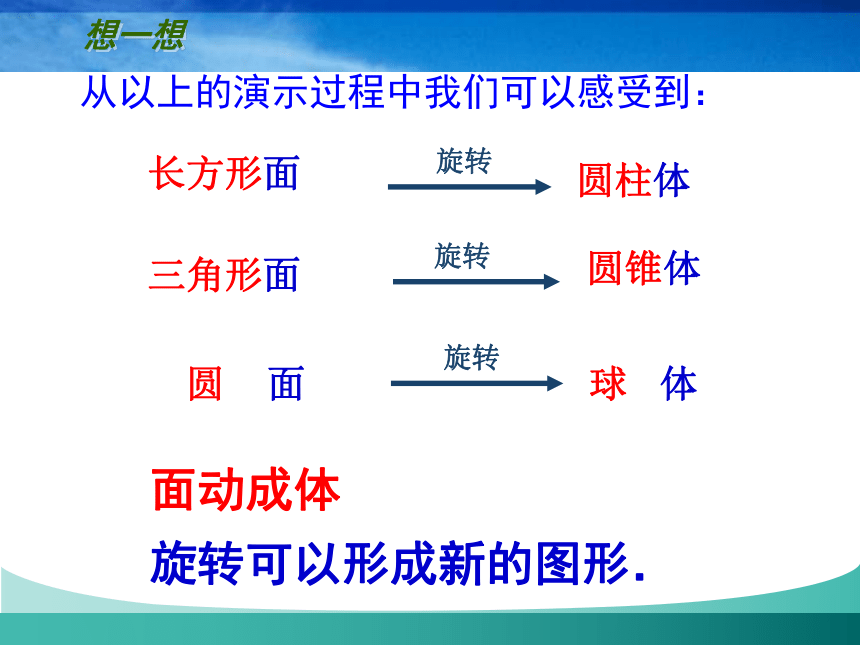
从以上的演示过程中我们可以感受到:
旋转
圆 面
球 体
圆柱体
长方形面
旋转
三角形面
圆锥体
旋转
面动成体
旋转可以形成新的图形.
想一想
点动成___
线
线动成___
面
面动成___
体
说一说
在下列两行图形中,分别找出相互对应的图形,并用线连接.
做一做
探索活动(二):1.翻折能否形成新的图形
翻折后图形与原图形比较,位置______.
翻折可以形成新的图形.
相反
图(1)是由图“回”向右平移而成的,将准备
好的纸片沿虚线剪开,
(1)怎样改变图形的位置可以得到图(2)?
(2)如果虚线以下的部分向右平移4格,得到
怎样的图形?
探索活动(二):2.平移能否形成新的图形
(图1)
(图2)
平移可以形成新的图形.
探索活动(二):2.平移能否形成新的图形
如何将直角三角尺由图(1)的位置旋转到图(2)与图(3)?
(1)
(2)
(3)
旋转可以形成新的图形.
探索活动(二):3.旋转能否形成新的图形
A
B
C
1.下列各图形中,不是由翻折而形成的是( )
C
小试牛刀
2.下列四个图形中,形成方法与另外三个不同的是( )
小试牛刀
B
(A)
(B)
(C)
(D)
旋转
翻折
平移
1.说一说下列图形的变化.
1.A B
3.C D
2.B C
层层推进
翻折
(1)
(2)
2.画出图案(1)沿虚线翻折后的图案
层层推进
1.将下图绕着点A旋转180 °,请你画出所得的图形.
A
大显身手
·
2.如图,将两块相同的直角三角尺的相等边拼在一起,能拼出几种不同的平面图形?你能说出这些图形的名称吗?
大显身手
等腰三角形
平行四边形
等腰三角形
平行四边形
长方形
筝形
效果图
_____________是图形运动的三种基本方式。
通过这三种运动只改变图形的 ,不改变图形的 。
翻折、平移、旋转
位置
形状和大小
【概括】
经历了本节课的
学习,你有什么收获?
思一思
本节课我们从图形运动变化的角度,举例说明了点、线、面、体之间的关系。经历了“图形的平移、旋转、翻折等运动变化的过程,进一步感受了图形之间的变换关系。
请你构造一些图案,使每一个图案中含有2个三角形、2个圆形和2条线段,并给图案加上适当的解说词.
稻草人:我们应该像稻草人一样有着坚强的意志
【做一做】 比比谁更有想象力.
例如:
我们生活的这个世界处在不停的运动和变化之中,人们不停地在研究这些运动和变化,并寻找规律……
5.2 图形的运动
观察下面的图片,你发现了什么?
点动成线
线动成面
O
A
B
A
交流与发现
你还能举出生活中“点动成线,线动成面”的例子吗
想一想
点动成线
感受点的运动
线 成面
动
动
感受线的运动
线
成面
动
感受线的运动
【探索活动一】
1.长方形纸板绕它的一条边旋转1周;
2.直角三角尺绕它的一条直角边旋转1周;
3.一枚硬币在桌面上竖直快速旋转.
它们分别形成怎样的几何体?
请同学们分小组讨论一下,说说你的猜想?
长方形绕一边旋转成圆柱体。
感受面的运动
直角三角形绕一直角
边旋转一周成圆锥体。
感受面的运动
3.一枚硬币在桌面上竖起快速旋转,形成怎样的几何体?
感受面的运动
从以上的演示过程中我们可以感受到:
旋转
圆 面
球 体
圆柱体
长方形面
旋转
三角形面
圆锥体
旋转
面动成体
旋转可以形成新的图形.
想一想
点动成___
线
线动成___
面
面动成___
体
说一说
在下列两行图形中,分别找出相互对应的图形,并用线连接.
做一做
探索活动(二):1.翻折能否形成新的图形
翻折后图形与原图形比较,位置______.
翻折可以形成新的图形.
相反
图(1)是由图“回”向右平移而成的,将准备
好的纸片沿虚线剪开,
(1)怎样改变图形的位置可以得到图(2)?
(2)如果虚线以下的部分向右平移4格,得到
怎样的图形?
探索活动(二):2.平移能否形成新的图形
(图1)
(图2)
平移可以形成新的图形.
探索活动(二):2.平移能否形成新的图形
如何将直角三角尺由图(1)的位置旋转到图(2)与图(3)?
(1)
(2)
(3)
旋转可以形成新的图形.
探索活动(二):3.旋转能否形成新的图形
A
B
C
1.下列各图形中,不是由翻折而形成的是( )
C
小试牛刀
2.下列四个图形中,形成方法与另外三个不同的是( )
小试牛刀
B
(A)
(B)
(C)
(D)
旋转
翻折
平移
1.说一说下列图形的变化.
1.A B
3.C D
2.B C
层层推进
翻折
(1)
(2)
2.画出图案(1)沿虚线翻折后的图案
层层推进
1.将下图绕着点A旋转180 °,请你画出所得的图形.
A
大显身手
·
2.如图,将两块相同的直角三角尺的相等边拼在一起,能拼出几种不同的平面图形?你能说出这些图形的名称吗?
大显身手
等腰三角形
平行四边形
等腰三角形
平行四边形
长方形
筝形
效果图
_____________是图形运动的三种基本方式。
通过这三种运动只改变图形的 ,不改变图形的 。
翻折、平移、旋转
位置
形状和大小
【概括】
经历了本节课的
学习,你有什么收获?
思一思
本节课我们从图形运动变化的角度,举例说明了点、线、面、体之间的关系。经历了“图形的平移、旋转、翻折等运动变化的过程,进一步感受了图形之间的变换关系。
请你构造一些图案,使每一个图案中含有2个三角形、2个圆形和2条线段,并给图案加上适当的解说词.
稻草人:我们应该像稻草人一样有着坚强的意志
【做一做】 比比谁更有想象力.
例如:
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
