苏科版七年级数学上册课件 第二章有理数2.6有理数的乘法与除法(共15张ppt)
文档属性
| 名称 | 苏科版七年级数学上册课件 第二章有理数2.6有理数的乘法与除法(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
2.6
有理数的乘法与除法(2)
1.有理数乘法法则:两数相乘,同号得正,异号得负,并把
绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
1.判断:
(1)同号两数相乘,取相同的符号,再把绝对值相乘;
(
)
(2)异号两数相乘,取绝对值较大的因数的符号;
(
)
(3)两数相乘,如果积为正数,则这两个因数都是正数;
(
)
(4)0乘以任何数都得0;
(
)
(5)几个数相乘,积的符号由负因数的个数确定。
(
)
×
×
×
√
×
小学里我们已经学习过了乘法的哪些运算律?
那么这些运算律在我们有理数的范围内还可以适用吗?
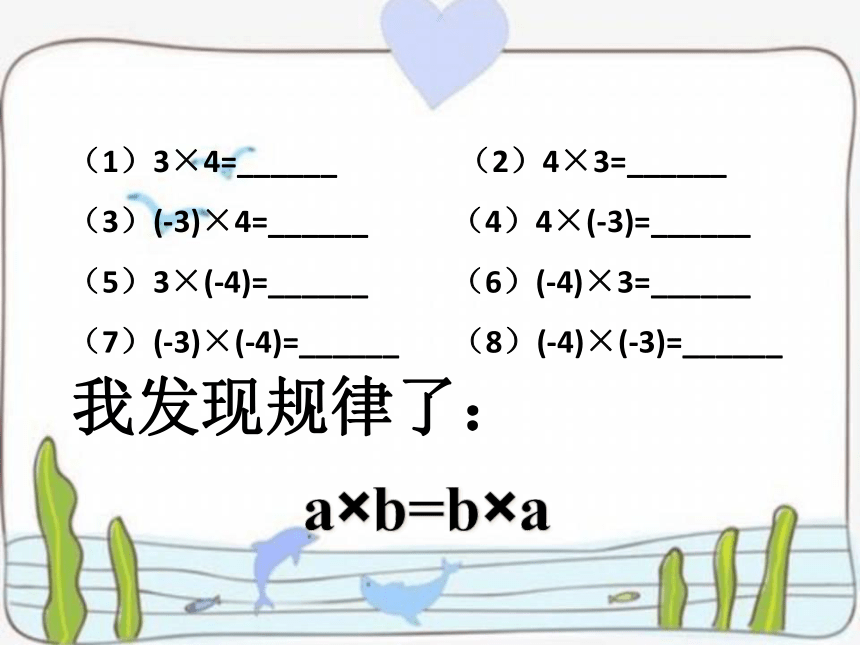
(1)3×4=______
(2)4×3=______
(3)(-3)×4=______
(4)4×(-3)=______
(5)3×(-4)=______
(6)(-4)×3=______
(7)(-3)×(-4)=______
(8)(-4)×(-3)=______
我发现规律了:
(1)(4×6)×5=______
4×(6×5)=______
(2)[(-3)×4]×0.5=______
(-3)×(4×0.5)=______
(3)[3×(-8)]×0.125=______
3×[(-8)×0.125]=______
我发现规律了:
?
我发现规律了:
有理数乘法运算律:
交换律:
a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:a×(b+c)=a×b+a×c
1.说出下面每一步计算的依据,并体会这样做的优越性:
(-0.4)×(-0.8)×(-1.25)×2.5
=-0.4×0.8×1.25×2.5
(
)
=-0.4×2.5×0.8×1.25
(
)
=-(0.4×2.5)
×(0.8×1.25)
(
)
=-1×1
=-1
计算:
?
?
1.倒数和相反数是两个重要的概念,你能说出两者的区别吗?
若a,b互为相反数,则a+b=
,a与b
为0(填“能”或“不能”)。
若a,b互为倒数,
则a·b=
,a与b
为0(填“能”或“不能”)。
2.(1)(
+
-
)×(-36)
(2)
(3)(-17)×43+(-17)×21-(-17)×164
(4)
3.(1)
(2)
(3)
4.
(1)24+(-1.6)×(-3)×(-5)×2
(2)(-47.65)×2+(-37.15)×(-2)+10.5×(-7)
(3)211×(-455)+365×455-211×545+545×365
(4)
总结:
1.有理数乘法运算律:(为了方便运算)
交换律:
a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:a×(b+c)=a×b+a×c
2.乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数。
2.6
有理数的乘法与除法(2)
1.有理数乘法法则:两数相乘,同号得正,异号得负,并把
绝对值相乘.任何数同0相乘,都得0.
2.几个不是零的数相乘,负因数的个数为
奇数时积为负数
偶数时积为正数
3.几个数相乘若有因数为零则积为零.
4.有理数乘法的求解步骤:
有理数相乘,先确定积的符号,再确定积的绝对值.
1.判断:
(1)同号两数相乘,取相同的符号,再把绝对值相乘;
(
)
(2)异号两数相乘,取绝对值较大的因数的符号;
(
)
(3)两数相乘,如果积为正数,则这两个因数都是正数;
(
)
(4)0乘以任何数都得0;
(
)
(5)几个数相乘,积的符号由负因数的个数确定。
(
)
×
×
×
√
×
小学里我们已经学习过了乘法的哪些运算律?
那么这些运算律在我们有理数的范围内还可以适用吗?
(1)3×4=______
(2)4×3=______
(3)(-3)×4=______
(4)4×(-3)=______
(5)3×(-4)=______
(6)(-4)×3=______
(7)(-3)×(-4)=______
(8)(-4)×(-3)=______
我发现规律了:
(1)(4×6)×5=______
4×(6×5)=______
(2)[(-3)×4]×0.5=______
(-3)×(4×0.5)=______
(3)[3×(-8)]×0.125=______
3×[(-8)×0.125]=______
我发现规律了:
?
我发现规律了:
有理数乘法运算律:
交换律:
a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:a×(b+c)=a×b+a×c
1.说出下面每一步计算的依据,并体会这样做的优越性:
(-0.4)×(-0.8)×(-1.25)×2.5
=-0.4×0.8×1.25×2.5
(
)
=-0.4×2.5×0.8×1.25
(
)
=-(0.4×2.5)
×(0.8×1.25)
(
)
=-1×1
=-1
计算:
?
?
1.倒数和相反数是两个重要的概念,你能说出两者的区别吗?
若a,b互为相反数,则a+b=
,a与b
为0(填“能”或“不能”)。
若a,b互为倒数,
则a·b=
,a与b
为0(填“能”或“不能”)。
2.(1)(
+
-
)×(-36)
(2)
(3)(-17)×43+(-17)×21-(-17)×164
(4)
3.(1)
(2)
(3)
4.
(1)24+(-1.6)×(-3)×(-5)×2
(2)(-47.65)×2+(-37.15)×(-2)+10.5×(-7)
(3)211×(-455)+365×455-211×545+545×365
(4)
总结:
1.有理数乘法运算律:(为了方便运算)
交换律:
a×b=b×a
结合律:(a×b)×c=a×(b×c)
分配律:a×(b+c)=a×b+a×c
2.乘积为1的两个数互为倒数,其中一个数叫做另一个数的倒数。
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
