数学:8.2《不等式的基本性质1》课件(华师大版七年级下)
文档属性
| 名称 | 数学:8.2《不等式的基本性质1》课件(华师大版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-07 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
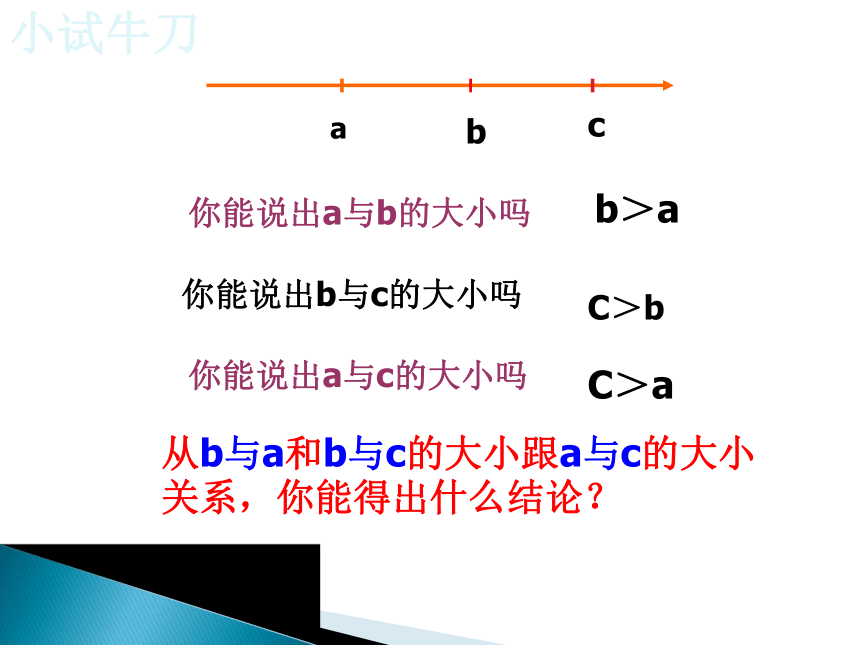
c
b
a
你能说出a与b的大小吗
你能说出b与c的大小吗
你能说出a与c的大小吗
b>a
C>b
C>a
从b与a和b与c的大小跟a与c的大小关系,你能得出什么结论?
小试牛刀
若a<b,b<c,则a<c。
不等式的传递性
你能举几个具体的例子说明吗?
(2)观察:用“<”或“>”填空,并找一找其中的规律.
(2) –1<3 , -1+2____3+2 , -1-3____3-3 ;
(3) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4) –2<3, (-2)×6____3×6 , (-2)×(-6)____3×(-6)
5>3, 5+2____3+2 , 5-2____3-2 ;
>
>
<
<
>
<
<
>
会发现:当不等式两边加或减去同一个数时,不等号的方向______
不变
当不等式的两边同乘同一个正数时,不等号的方向______;而乘同一个负数时,不等号的方向________.
不变
改变
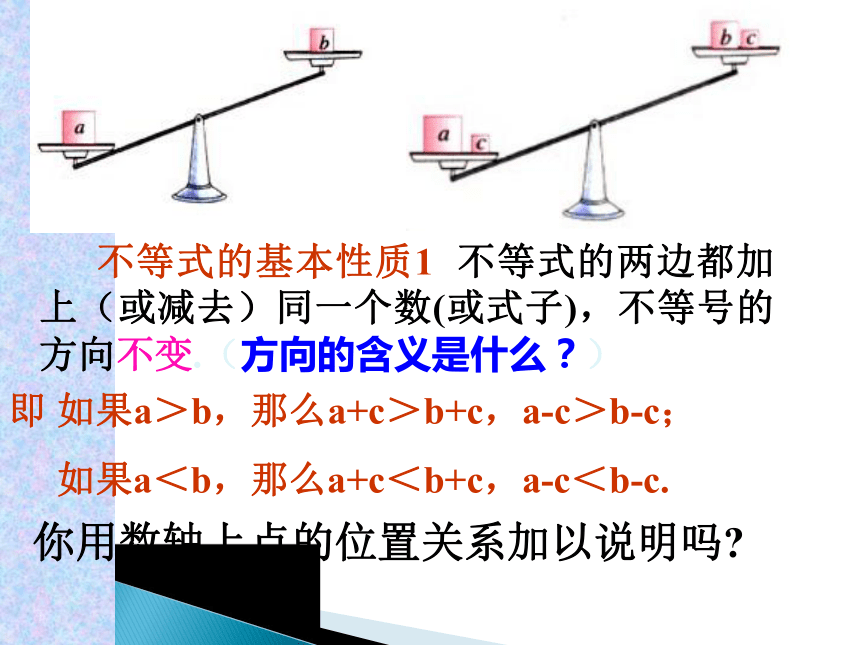
不等式的基本性质1 不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变.(方向的含义是什么?)
即 如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
你用数轴上点的位置关系加以说明吗
不访设c>0,则
a
b
b+c
a+c
c
c
可见,a+c>b+c
a
b
b-c
a-c
c
c
可见,a-c>b-c
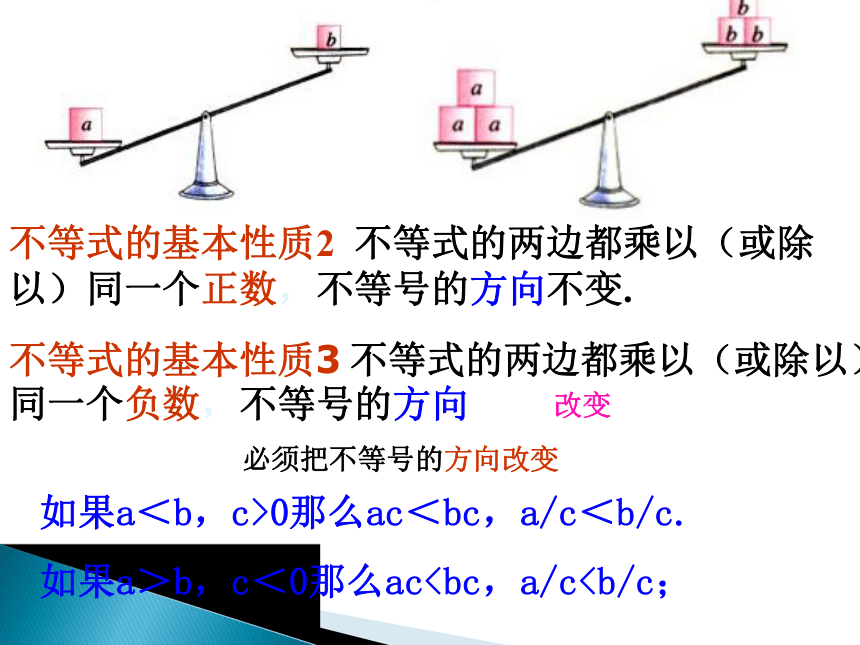
不等式的基本性质2 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3 不等式的两边都乘以(或除以)同一个负数,不等号的方向
改变
必须把不等号的方向改变
如果a<b,c>0那么ac<bc,a/c<b/c.
如果a>b,c<0那么ac选择适当的不等号填空:
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>
>
<
3 >1
例 已知a<0 ,试比较2a与a的大小。
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a
0
a
2a
∣a∣
∣a∣
想一想:还有其他比较2a与a的大小的方法吗?
∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a 探究活动
比较等式与不等式的基本性质.
例如,等式是否有与不等式类似的传递性?不等式是否有与等式的基本性质类似的移项法则?你可以用列表的方式进行对比.(请与你的伙伴交流)
通过这节课的学习活动你有哪些收获?
c
b
a
你能说出a与b的大小吗
你能说出b与c的大小吗
你能说出a与c的大小吗
b>a
C>b
C>a
从b与a和b与c的大小跟a与c的大小关系,你能得出什么结论?
小试牛刀
若a<b,b<c,则a<c。
不等式的传递性
你能举几个具体的例子说明吗?
(2)观察:用“<”或“>”填空,并找一找其中的规律.
(2) –1<3 , -1+2____3+2 , -1-3____3-3 ;
(3) 6>2, 6×5____2×5 , 6×(-5)____2×(-5) ;
(4) –2<3, (-2)×6____3×6 , (-2)×(-6)____3×(-6)
5>3, 5+2____3+2 , 5-2____3-2 ;
>
>
<
<
>
<
<
>
会发现:当不等式两边加或减去同一个数时,不等号的方向______
不变
当不等式的两边同乘同一个正数时,不等号的方向______;而乘同一个负数时,不等号的方向________.
不变
改变
不等式的基本性质1 不等式的两边都加上(或减去)同一个数(或式子),不等号的方向不变.(方向的含义是什么?)
即 如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
你用数轴上点的位置关系加以说明吗
不访设c>0,则
a
b
b+c
a+c
c
c
可见,a+c>b+c
a
b
b-c
a-c
c
c
可见,a-c>b-c
不等式的基本性质2 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
不等式的基本性质3 不等式的两边都乘以(或除以)同一个负数,不等号的方向
改变
必须把不等号的方向改变
如果a<b,c>0那么ac<bc,a/c<b/c.
如果a>b,c<0那么ac
(1)∵0 1,
∴ a a+1(不等式的基本性质1);
(2)∵(a-1)2 0,
∴(a-1)2-2 -2(不等式的基本性质1)
(3)若x+1>0,两边同加上-1,得____________
(依据:_____________________).
(4)若2 x >-6,两边同除以2,得________,依据_______________.
(5)若-0.5 x≤1,两边同乘以-2,得________,依据___________
<
<
≥
≥
x >-1
不等式的基本性质1
x >-3
不等式的基本性质2
X≥-2
不等式的基本性质3
1.若-m>5,则m -5.
2.如果x/y>0, 那么xy 0.
3.如果a>-1,那么a-b -1-b.
4.-0.9<-0.3,两边都除以(-0.3),得_______.
>
>
<
3 >1
例 已知a<0 ,试比较2a与a的大小。
解法一:∵2>1,a<0,
∴2a<a(不等式的基本性质3)
解法二: 在数轴上分别表示2a和a的点(a<0),如图.2a位于a的左边,所以2a<a
0
a
2a
∣a∣
∣a∣
想一想:还有其他比较2a与a的大小的方法吗?
∵ 2a-a=a, 又∵ a<0,
∴ 2a-a<0,
∴2a
比较等式与不等式的基本性质.
例如,等式是否有与不等式类似的传递性?不等式是否有与等式的基本性质类似的移项法则?你可以用列表的方式进行对比.(请与你的伙伴交流)
通过这节课的学习活动你有哪些收获?
