数学:9.1《三角形的三边关系》课件(华师大版七年级下)
文档属性
| 名称 | 数学:9.1《三角形的三边关系》课件(华师大版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-07 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
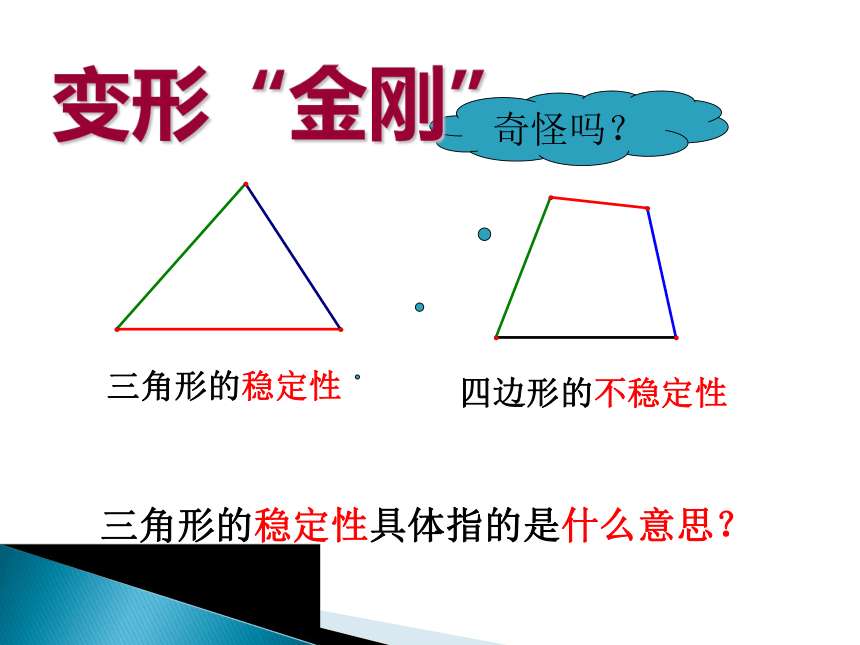
三角形的三边关系
三角形的稳定性
四边形的不稳定性
三角形的稳定性具体指的是什么意思?
奇怪吗?
变形“金刚”
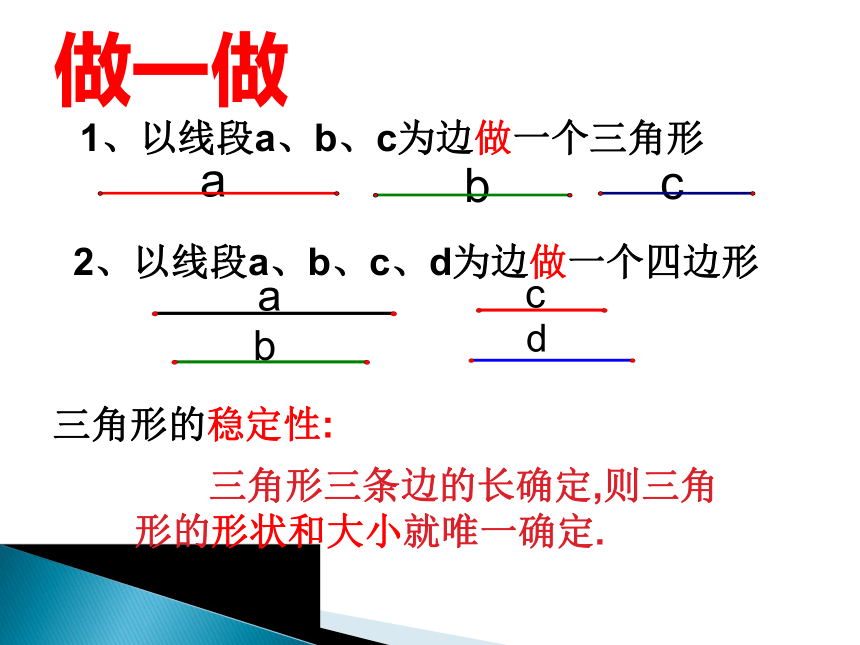
1、以线段a、b、c为边做一个三角形
a
b
c
做一做
2、以线段a、b、c、d为边做一个四边形
三角形的稳定性:
三角形三条边的长确定,则三角形的形状和大小就唯一确定.
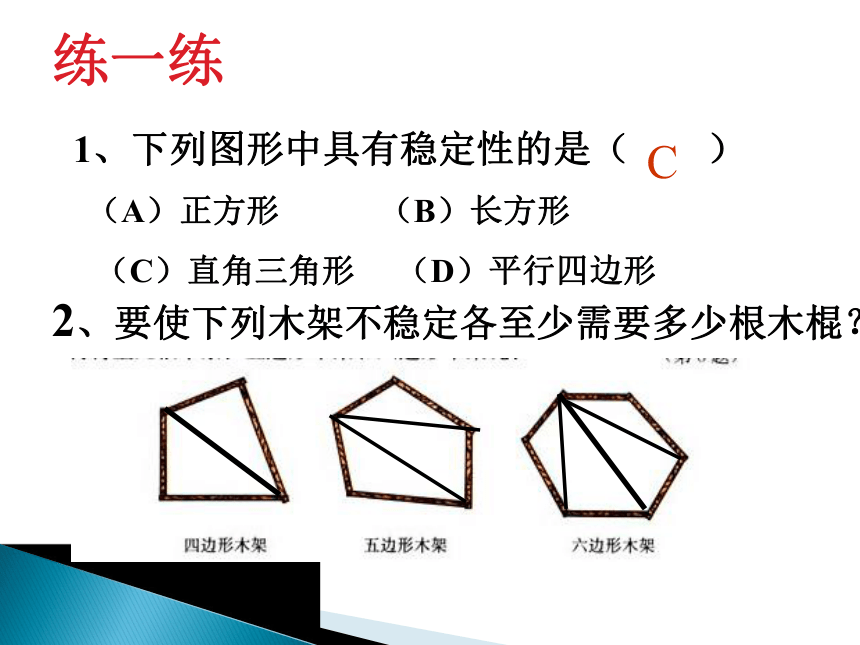
练一练
1、下列图形中具有稳定性的是( )
(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形
2、要使下列木架不稳定各至少需要多少根木棍?
C
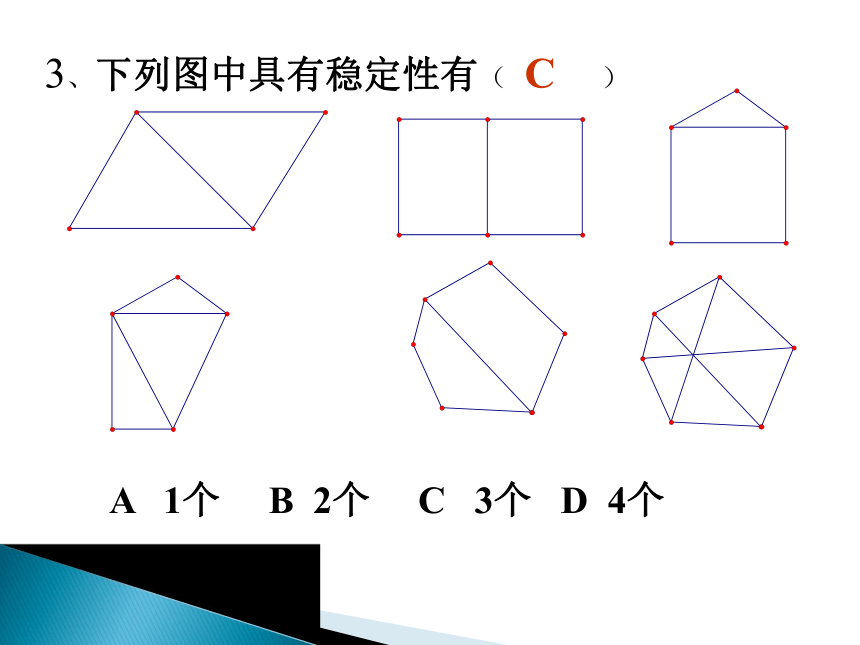
3、下列图中具有稳定性有( )
A 1个 B 2个 C 3个 D 4个
C
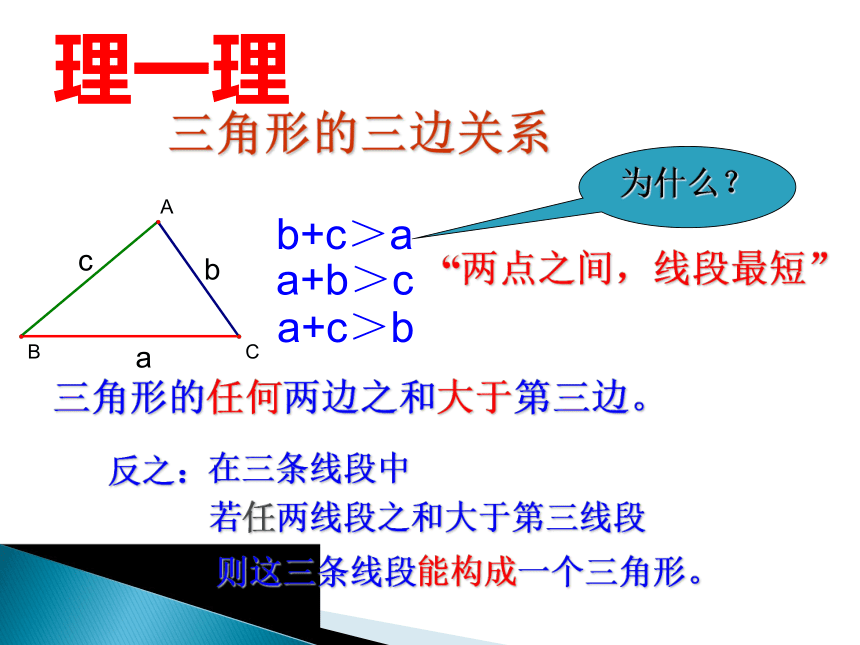
三角形的三边关系
“两点之间,线段最短”
a+b>c
b+c>a
a+c>b
三角形的任何两边之和大于第三边。
为什么?
反之:
在三条线段中
若任两线段之和大于第三线段
则这三条线段能构成一个三角形。
理一理
画一画
画一个三角形,使它的三条边长分别为7cm、5cm、4cm.
以下列长度的各组线段为边,画一个三角形.
试一试
2
(1)5cm,4cm,3cm;
(2)9cm,5cm,4cm;
(3)7cm,4cm,2cm;
4、判断:已知a+b>c,则以线段a、b、c为边能够成三角形。( )
5、在ΔABC中,AB=9,BC=2,并且AC为奇数,那么ΔABC的周长为 。
6、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差 。
2
20
三角形较短两边之和大于第三边。
(3)3 cm、8 cm、5 cm;
(4)4 cm、5 cm、6 cm.
(1) 15cm、10 cm、7 cm;
(2)4 cm、5 cm、10 cm;
下列长度的各组线段能否组成一个三角形?
判一判
已知三角形两边a、b长为 9、5,
则第三边c的取值范围 。
三角形的任何两边之差小于第三边。
|a-b|< c<a+b
想一想
三角形的任何两边之和大于第三边。
鲁班给徒弟两根树,一根长八尺,另一根长一丈二尺,要想做屋架,你帮徒弟想一想,第三根树应多长?
屋架为什么做成三角形
议一议
四边形的不稳定性有用呢?
4尺<c<20尺
C=8尺
C=12尺
已知: 等腰三角形周长为11,边长都为整数.求:三边的长.
考考你
5、5、1
5、3、3
4、4、3
1、5、5
5、3、3
3、4、4
3、3、5
4、4、3
5、5、1
先考虑最大边
方法1:
方法2:
先考虑底边
方法3:
先考虑腰
若一平面上有A、B、C三个点,则
①AB+AC BC
②若AB+AC>BC 则以A、B、C为顶点一定能构成△ ABC吗?
≥
A
B
C
A
B
C
拓展一步
请你决策
如图A、B、C、D为四个村庄,现在这四个村打算造个学校,为了使学校到四个村庄的距离之和最小,请问校址选在哪里?
PA+PB+PC+PD
(PA+PC)+(PB+PD)
=
AC+BD
≥
谈谈你的收获和感受.
1.三角形的稳定性.
3.三角形的三边关系.
2.已知三边画三角形.
4.画图、拼接、翻折
1.数学就在我们身边
2.数学有趣又有用.
3.数学激发了我们的
4.在动手、动脑、交流
等实验方法是探索
数学奥秘的常用手段.
好奇心.
中提高.
作业
三角形的三边关系
三角形的稳定性
四边形的不稳定性
三角形的稳定性具体指的是什么意思?
奇怪吗?
变形“金刚”
1、以线段a、b、c为边做一个三角形
a
b
c
做一做
2、以线段a、b、c、d为边做一个四边形
三角形的稳定性:
三角形三条边的长确定,则三角形的形状和大小就唯一确定.
练一练
1、下列图形中具有稳定性的是( )
(A)正方形 (B)长方形
(C)直角三角形 (D)平行四边形
2、要使下列木架不稳定各至少需要多少根木棍?
C
3、下列图中具有稳定性有( )
A 1个 B 2个 C 3个 D 4个
C
三角形的三边关系
“两点之间,线段最短”
a+b>c
b+c>a
a+c>b
三角形的任何两边之和大于第三边。
为什么?
反之:
在三条线段中
若任两线段之和大于第三线段
则这三条线段能构成一个三角形。
理一理
画一画
画一个三角形,使它的三条边长分别为7cm、5cm、4cm.
以下列长度的各组线段为边,画一个三角形.
试一试
2
(1)5cm,4cm,3cm;
(2)9cm,5cm,4cm;
(3)7cm,4cm,2cm;
4、判断:已知a+b>c,则以线段a、b、c为边能够成三角形。( )
5、在ΔABC中,AB=9,BC=2,并且AC为奇数,那么ΔABC的周长为 。
6、如图,已知BM是ΔABC的中线,AB=6,BC=8,那么ΔMBC的周长与ΔABM的周长相差 。
2
20
三角形较短两边之和大于第三边。
(3)3 cm、8 cm、5 cm;
(4)4 cm、5 cm、6 cm.
(1) 15cm、10 cm、7 cm;
(2)4 cm、5 cm、10 cm;
下列长度的各组线段能否组成一个三角形?
判一判
已知三角形两边a、b长为 9、5,
则第三边c的取值范围 。
三角形的任何两边之差小于第三边。
|a-b|< c<a+b
想一想
三角形的任何两边之和大于第三边。
鲁班给徒弟两根树,一根长八尺,另一根长一丈二尺,要想做屋架,你帮徒弟想一想,第三根树应多长?
屋架为什么做成三角形
议一议
四边形的不稳定性有用呢?
4尺<c<20尺
C=8尺
C=12尺
已知: 等腰三角形周长为11,边长都为整数.求:三边的长.
考考你
5、5、1
5、3、3
4、4、3
1、5、5
5、3、3
3、4、4
3、3、5
4、4、3
5、5、1
先考虑最大边
方法1:
方法2:
先考虑底边
方法3:
先考虑腰
若一平面上有A、B、C三个点,则
①AB+AC BC
②若AB+AC>BC 则以A、B、C为顶点一定能构成△ ABC吗?
≥
A
B
C
A
B
C
拓展一步
请你决策
如图A、B、C、D为四个村庄,现在这四个村打算造个学校,为了使学校到四个村庄的距离之和最小,请问校址选在哪里?
PA+PB+PC+PD
(PA+PC)+(PB+PD)
=
AC+BD
≥
谈谈你的收获和感受.
1.三角形的稳定性.
3.三角形的三边关系.
2.已知三边画三角形.
4.画图、拼接、翻折
1.数学就在我们身边
2.数学有趣又有用.
3.数学激发了我们的
4.在动手、动脑、交流
等实验方法是探索
数学奥秘的常用手段.
好奇心.
中提高.
作业
