数学:10.3《等腰三角形性质综合应用》课件(华师大版七年级下)
文档属性
| 名称 | 数学:10.3《等腰三角形性质综合应用》课件(华师大版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 515.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-07 00:00:00 | ||
图片预览




文档简介
(共11张PPT)
学习目标:
1、知识与技能目标:进一步熟悉和掌握等腰三角形的性质,能灵活的使用性质解决相关题目,培养学生的逻辑推理能力,语言表述能力。
2、过程与方法目标:通过学生的分析,练习,使学生能进一步理解知识,准确运用。
3、情感与态度目标:学生通过积极参与感受到一题多解的乐趣,激发学生的学习兴趣。
学习难点:熟练、准确应用“三线合一”,文字叙述与字母符号的转换。
1、等腰三角形的性质有那些?
(1)等腰三角形是轴对称图形;
(2)等腰三角形的两腰相等;
(3)等腰三角形的两底角相等;(简称:等边对等角。相关定理还有:大边对大角;小边对小角)
(4)等腰三角形的底边上的中线、底边上的高线、顶角的角平分线互相重合;(简称:三线合一)
(5)等边三角形的每个内角都相等,都等于60°
2、性质定理与判定定理有什么样的关系?
互为逆定理。
3、等腰三角形的判定定理有哪些?
(1)有两边相等的三角形叫做等腰三角形。(其定义是重要的判定)
(2)有两个角相等的三角形是等腰三角形。
(3)一边上的中线、这边上的高线与这边所对的角的角平分线中任意两条线互相重合的三角形是等腰三角形。(三线合一的逆定理,当中包含三个定理)
(4)三个角相等的三角形是等边三角形。
二、新课过程:
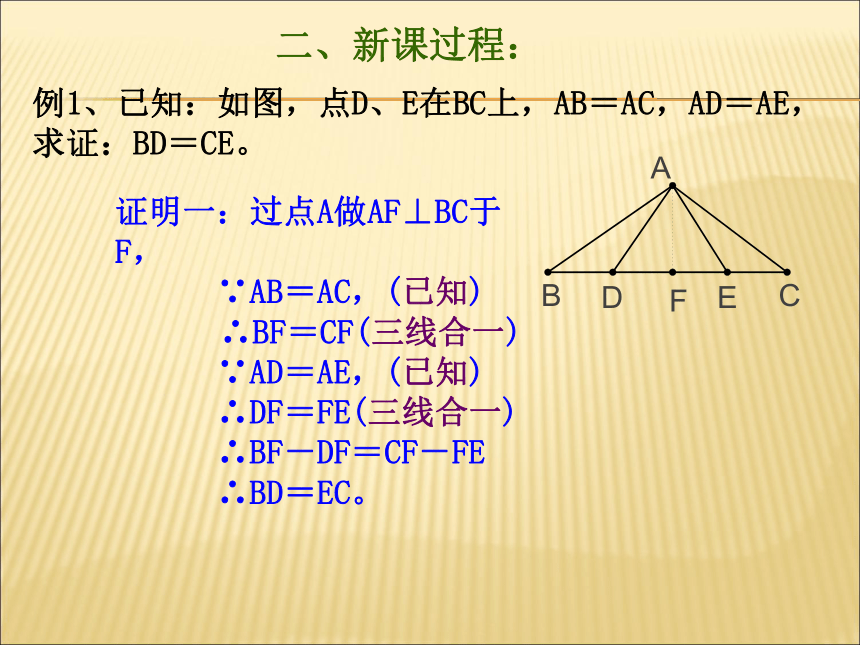
例1、已知:如图,点D、E在BC上,AB=AC,AD=AE,求证:BD=CE。
证明一:过点A做AF⊥BC于F,
∵AB=AC,(已知)
∴BF=CF(三线合一)
∵AD=AE,(已知)
∴DF=FE(三线合一)
∴BF-DF=CF-FE
∴BD=EC。
证明二:作BC边上中点,连结AF。
∴BF=FC
∵AB=AC
∴AF⊥DE(三线合一)
又∵AD=AE
∴DF=FE(三线合一)
∴BF-DF=CF-FE
∴BD=EC。
证明:作∠BAC的平分线,交BC于F。
∵AB=AC
∴BF=CF(三线合一)
AF⊥DE(三线合一)
又∵AD=AE
∴DF=FE(三线合一)
∴BF-DF=CF-FE
∴BD=EC。
问:这样的题,我们首先应做什么?
弄清题意,画出符合题意的图形,并写出已知、求证。
已知:如图,在ΔABC中,AB=AC,D是BC边上中点,DE⊥AB于E,DF⊥AC于F,求证:DE=DF。
请先行独立思考。
已知:如图,在ΔABC中,AB=AC,D是BC边上中点,DE⊥AB于E,DF⊥AC于F,求证:DE=DF。
证明:连结AD。
∵AB=AC
∴∠BAD=∠CAD
又∵DE⊥AB,DF⊥AC
∴DE=DF(角平分线上的点到角两边的距离相等)
学习目标:
1、知识与技能目标:进一步熟悉和掌握等腰三角形的性质,能灵活的使用性质解决相关题目,培养学生的逻辑推理能力,语言表述能力。
2、过程与方法目标:通过学生的分析,练习,使学生能进一步理解知识,准确运用。
3、情感与态度目标:学生通过积极参与感受到一题多解的乐趣,激发学生的学习兴趣。
学习难点:熟练、准确应用“三线合一”,文字叙述与字母符号的转换。
1、等腰三角形的性质有那些?
(1)等腰三角形是轴对称图形;
(2)等腰三角形的两腰相等;
(3)等腰三角形的两底角相等;(简称:等边对等角。相关定理还有:大边对大角;小边对小角)
(4)等腰三角形的底边上的中线、底边上的高线、顶角的角平分线互相重合;(简称:三线合一)
(5)等边三角形的每个内角都相等,都等于60°
2、性质定理与判定定理有什么样的关系?
互为逆定理。
3、等腰三角形的判定定理有哪些?
(1)有两边相等的三角形叫做等腰三角形。(其定义是重要的判定)
(2)有两个角相等的三角形是等腰三角形。
(3)一边上的中线、这边上的高线与这边所对的角的角平分线中任意两条线互相重合的三角形是等腰三角形。(三线合一的逆定理,当中包含三个定理)
(4)三个角相等的三角形是等边三角形。
二、新课过程:
例1、已知:如图,点D、E在BC上,AB=AC,AD=AE,求证:BD=CE。
证明一:过点A做AF⊥BC于F,
∵AB=AC,(已知)
∴BF=CF(三线合一)
∵AD=AE,(已知)
∴DF=FE(三线合一)
∴BF-DF=CF-FE
∴BD=EC。
证明二:作BC边上中点,连结AF。
∴BF=FC
∵AB=AC
∴AF⊥DE(三线合一)
又∵AD=AE
∴DF=FE(三线合一)
∴BF-DF=CF-FE
∴BD=EC。
证明:作∠BAC的平分线,交BC于F。
∵AB=AC
∴BF=CF(三线合一)
AF⊥DE(三线合一)
又∵AD=AE
∴DF=FE(三线合一)
∴BF-DF=CF-FE
∴BD=EC。
问:这样的题,我们首先应做什么?
弄清题意,画出符合题意的图形,并写出已知、求证。
已知:如图,在ΔABC中,AB=AC,D是BC边上中点,DE⊥AB于E,DF⊥AC于F,求证:DE=DF。
请先行独立思考。
已知:如图,在ΔABC中,AB=AC,D是BC边上中点,DE⊥AB于E,DF⊥AC于F,求证:DE=DF。
证明:连结AD。
∵AB=AC
∴∠BAD=∠CAD
又∵DE⊥AB,DF⊥AC
∴DE=DF(角平分线上的点到角两边的距离相等)
