数学:10.3《等腰三角形有关计算问题》课件(华师大版七年级下)
文档属性
| 名称 | 数学:10.3《等腰三角形有关计算问题》课件(华师大版七年级下) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-07 21:33:00 | ||
图片预览




文档简介
(共13张PPT)
学习目标:
1、知识与技能目标:通过学生积极参与思考、练习、掌握一类有关通过计算去证明、解决的题目,进一步熟悉等腰三角形的性质与判定。
2、过程与方法目标:讲练结合,以练为主,学生归纳解题中的规律,在解题中培养学生的能力。
3、情感与态度目标:体会数学内在的和谐美、感受自身能力增长的快乐。
学习难点:分析归纳出解题方法,解决问题。
等腰三角形的性质定理有哪些?
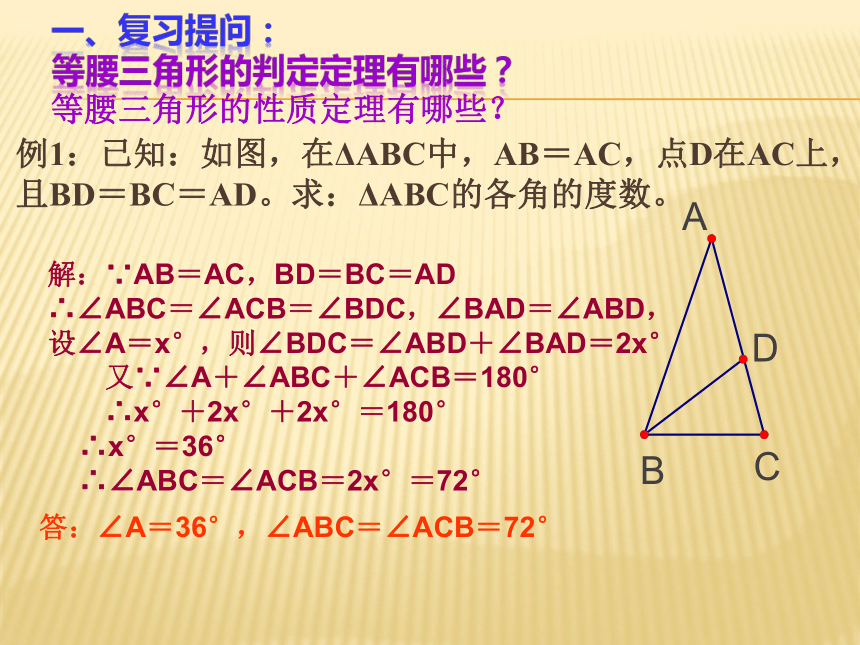
例1:已知:如图,在ΔABC中,AB=AC,点D在AC上,且BD=BC=AD。求:ΔABC的各角的度数。
解:∵AB=AC,BD=BC=AD
∴∠ABC=∠ACB=∠BDC,∠BAD=∠ABD,
设∠A=x°,则∠BDC=∠ABD+∠BAD=2x°
又∵∠A+∠ABC+∠ACB=180°
∴x°+2x°+2x°=180°
∴x°=36°
∴∠ABC=∠ACB=2x°=72°
答:∠A=36°,∠ABC=∠ACB=72°
当题目中出现有较多相等的线段,众多的角之间的关系,情况比较复杂时,用下面的方法做到化繁为简,迅速解题。
①由相等的线段,根据“等边对等角”得出相应相等的角,弄清各角之间关系;
②设最小的角为x,其余各角用含x的式子表示出来;(想想:为什么要设最小的角为x呢?使其它角与最小的角用倍数关系表达。)
③找一个合适的三角形,用三角形的内角和定理列方程解之。
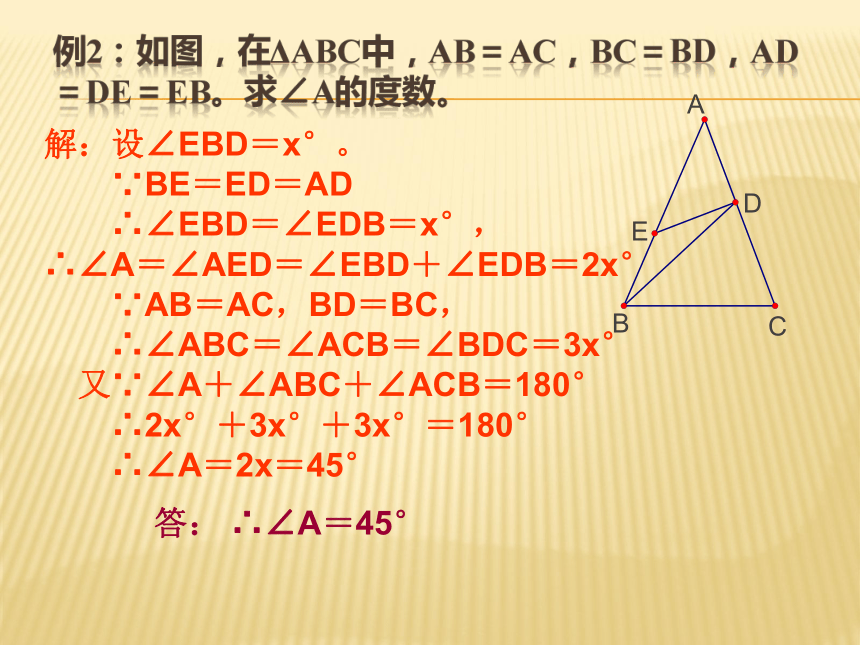
解:设∠EBD=x°。
∵BE=ED=AD
∴∠EBD=∠EDB=x°,
∴∠A=∠AED=∠EBD+∠EDB=2x°
∵AB=AC,BD=BC,
∴∠ABC=∠ACB=∠BDC=3x°
又∵∠A+∠ABC+∠ACB=180°
∴2x°+3x°+3x°=180°
∴∠A=2x=45°
答: ∴∠A=45°
解:设∠CAB=x°
∵AB=BB1=AA1
∴∠B1=∠CAB=x°
∴∠B1AD=2x°
又∵BB1平分∠DBC
∴∠CBD=4x°
∴∠AA1B=∠ABA1=∠CBD=4x°
又∵A1A平分∠EAB,
∴∠A1AB=
∵∠A1AB+∠AA1B+∠ABA1=180°
∴∠BAC=x°=12°
∴
+4x°+4x°=180°
答:∴∠BAC=12°
证明:设∠A=x°,∠B=y°
∵AD=DC=DB
∴∠ACD=∠A=x°;
∠DCB=∠B=y°
∴2x°+2y°=180°
∴x°+y°=90°
即:∠ACB=90°
问:在这里,x、y的大小能具体的求出来吗?
不能,因为,x、y的大小可以变化。
但x、y的和能够求出来,它就是我们需要的结论。
答:100°
解:设∠A=x°,
∵AE=AC,
∴∠ECA=
∠B=90°-∠A=90°-x°
又∵BD=BC,
∴∠BDC=∠BCD=
∴∠ECD=180°-∠BDC-∠AEC=180°-135°=45°
答: ∠ECD=45°
解:设∠BAP=x°,∠QAC=y°
又∵MP是AB的垂直平分线(已知)
∴∠B=∠BAP=x°,
∵NQ是AC的垂直平分线,
∴∠C=∠CAQ=y°,
∴x°+y°=180°-∠BAC=50°
∴∠PAQ=∠BAC-x°-y°=80°
答: ∠PAQ=80°
学习目标:
1、知识与技能目标:通过学生积极参与思考、练习、掌握一类有关通过计算去证明、解决的题目,进一步熟悉等腰三角形的性质与判定。
2、过程与方法目标:讲练结合,以练为主,学生归纳解题中的规律,在解题中培养学生的能力。
3、情感与态度目标:体会数学内在的和谐美、感受自身能力增长的快乐。
学习难点:分析归纳出解题方法,解决问题。
等腰三角形的性质定理有哪些?
例1:已知:如图,在ΔABC中,AB=AC,点D在AC上,且BD=BC=AD。求:ΔABC的各角的度数。
解:∵AB=AC,BD=BC=AD
∴∠ABC=∠ACB=∠BDC,∠BAD=∠ABD,
设∠A=x°,则∠BDC=∠ABD+∠BAD=2x°
又∵∠A+∠ABC+∠ACB=180°
∴x°+2x°+2x°=180°
∴x°=36°
∴∠ABC=∠ACB=2x°=72°
答:∠A=36°,∠ABC=∠ACB=72°
当题目中出现有较多相等的线段,众多的角之间的关系,情况比较复杂时,用下面的方法做到化繁为简,迅速解题。
①由相等的线段,根据“等边对等角”得出相应相等的角,弄清各角之间关系;
②设最小的角为x,其余各角用含x的式子表示出来;(想想:为什么要设最小的角为x呢?使其它角与最小的角用倍数关系表达。)
③找一个合适的三角形,用三角形的内角和定理列方程解之。
解:设∠EBD=x°。
∵BE=ED=AD
∴∠EBD=∠EDB=x°,
∴∠A=∠AED=∠EBD+∠EDB=2x°
∵AB=AC,BD=BC,
∴∠ABC=∠ACB=∠BDC=3x°
又∵∠A+∠ABC+∠ACB=180°
∴2x°+3x°+3x°=180°
∴∠A=2x=45°
答: ∴∠A=45°
解:设∠CAB=x°
∵AB=BB1=AA1
∴∠B1=∠CAB=x°
∴∠B1AD=2x°
又∵BB1平分∠DBC
∴∠CBD=4x°
∴∠AA1B=∠ABA1=∠CBD=4x°
又∵A1A平分∠EAB,
∴∠A1AB=
∵∠A1AB+∠AA1B+∠ABA1=180°
∴∠BAC=x°=12°
∴
+4x°+4x°=180°
答:∴∠BAC=12°
证明:设∠A=x°,∠B=y°
∵AD=DC=DB
∴∠ACD=∠A=x°;
∠DCB=∠B=y°
∴2x°+2y°=180°
∴x°+y°=90°
即:∠ACB=90°
问:在这里,x、y的大小能具体的求出来吗?
不能,因为,x、y的大小可以变化。
但x、y的和能够求出来,它就是我们需要的结论。
答:100°
解:设∠A=x°,
∵AE=AC,
∴∠ECA=
∠B=90°-∠A=90°-x°
又∵BD=BC,
∴∠BDC=∠BCD=
∴∠ECD=180°-∠BDC-∠AEC=180°-135°=45°
答: ∠ECD=45°
解:设∠BAP=x°,∠QAC=y°
又∵MP是AB的垂直平分线(已知)
∴∠B=∠BAP=x°,
∵NQ是AC的垂直平分线,
∴∠C=∠CAQ=y°,
∴x°+y°=180°-∠BAC=50°
∴∠PAQ=∠BAC-x°-y°=80°
答: ∠PAQ=80°
