六年级数学上册课件 比的应用 人教版(共19张PPT)
文档属性
| 名称 | 六年级数学上册课件 比的应用 人教版(共19张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-06-11 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
教学目标
1.复习按一定比例来分配一个数量的意义。
2.
根据题中所给的比,掌握各部分量占总量的几分之几,能熟练地计算各部分量。
3.
感受比在生活中的广泛应用,提高解决问题的能力。
大班
小班
3个
2个
6个
4个
30个
20个
……
……
分到不能分为止
把这些橘子分给大班和小班,怎么分合理?
把这些橘子分给大班和小班,怎么分合理?
如果有140个橘子,按3︰2又应该怎样分?
3:2?
如果有140个橘子,按3︰2来分
可以把大班分得的个数看作(
)份,小班分得的个数看作(
)份。这筐橘子共有(
)份
小班分得的橘子个数是大班的(
),
大班分得的橘子数是小班的(
),
大班的分得得橘子数占这筐橘子的(
),
3
2
5
小班的分得得橘子数占这筐橘子的(
),
把这些橘子分给大班和小班,怎么分合理?
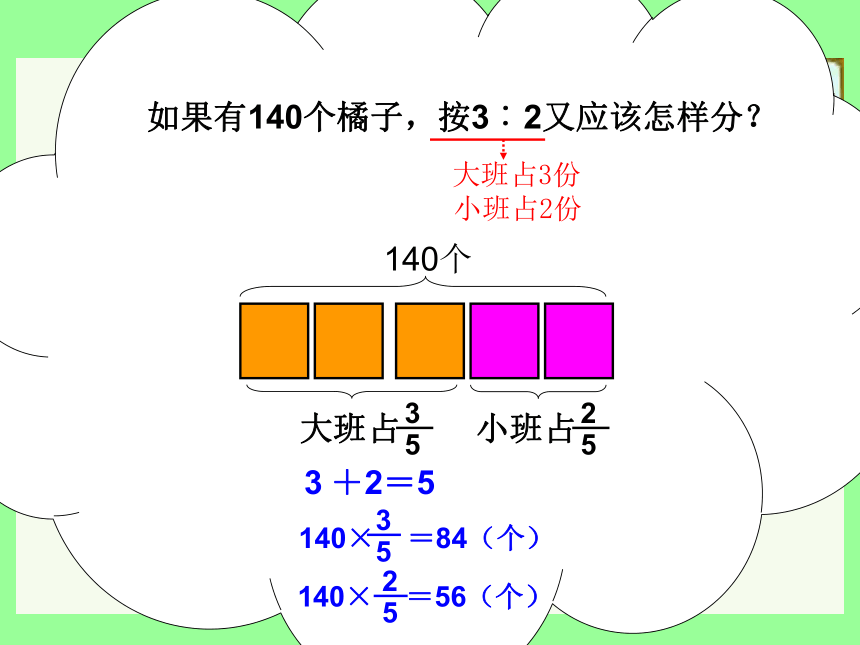
如果有140个橘子,按3︰2又应该怎样分?
大班占3份
小班占2份
大班占
5
3
小班占
5
2
140个
3
+2=5
140×
=56(个)
5
2
140×
=84(个)
5
3
李明与黄华合办股份制食品有限公司,李明出资10万元,黄华出资20万元,两年后盈利90万元,怎样分配利润才合理?
在工农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。这种分配方法通常叫做按比例分配。
第一步:求平均分的总份数
第二步:用除法求每部分是多少?
第三步:按照每部分占几份用乘法求出每部分是多少。
转化成
按比例分配应用题一般步骤:
解法一·:
分什么,有多少?
总数量
怎样分?
()︰()︰()
求平均分的总份数
求每部分占总数量的几分之几是多少?
用分数乘法求出每部分是多少。
转化成
按比例分配应用题一般步骤:
解法二:
务必掌握的四种类型的题目:
题型1:已知总量,各部分量之间的比求部分量
题型2:已知一个部分量及它与另一个部分量的比,求另一个部分量
题型3:已知一个部分量及它与另一个部分量的比,求总量
题型4:已知两个部分量的比以及差,求部分量或总量
试一试
小清要调制2200克巧克力奶,巧克力与奶的质量比是2︰9。需要巧克力和奶各多少克?
2+9=11
2200×
=400(克)
11
2
答:需要巧克力400克,奶1800克。
2200×
=1800(克)
11
9
试一试
小清要调制2200克巧克力奶,巧克力与奶的质量比是2︰9。需要巧克力和奶各多少克?
2+9=11(份)
2200÷11=200(克)
200
×2=400
(克)
200
×9=1800
(克)
答:需要巧克力400克,奶1800克。
六年级男生人数与女生人数的比是4:5,男生有16人,女生有多少人?六年级共有多少人?
16÷4=4(人)
4×5=20(人)
20+16=36
(人)
答:六年级有女生20人,共有36名学生。
一种什锦糖是由奶糖、水果糖和酥糖按
照2︰5︰3混合成的。要配制这样的什锦
糖500千克,需要奶糖、水果糖和酥糖各
多少千克?
用48厘米的铁丝围成一个长方形,这个长方形长和宽的比是5∶3,这个长方形长和宽各是多少?
48÷2=24(厘米)
5+3=8
答:这个长方形的长是15厘米,宽是9厘米。
24×
=15(厘米)
8
5
24×
=
9
(厘米)
8
3
用120厘米的铁丝做一个长方体的框架。长、宽、高的比是3:2:1。这个长方体的长、宽、高分别是多少?体积是多少?
5-3=2(份)24÷2=12(个)
5+3=8
(份)12×8=96(个)
体育用品商店里排球比篮球少24个,排球与篮球个数的比是3:5,排球和篮球一共有多少个?
本课小结
能运用比的意义解决按照一定的比进行分配的实际问题,进一步体会比的意义。
教学目标
1.复习按一定比例来分配一个数量的意义。
2.
根据题中所给的比,掌握各部分量占总量的几分之几,能熟练地计算各部分量。
3.
感受比在生活中的广泛应用,提高解决问题的能力。
大班
小班
3个
2个
6个
4个
30个
20个
……
……
分到不能分为止
把这些橘子分给大班和小班,怎么分合理?
把这些橘子分给大班和小班,怎么分合理?
如果有140个橘子,按3︰2又应该怎样分?
3:2?
如果有140个橘子,按3︰2来分
可以把大班分得的个数看作(
)份,小班分得的个数看作(
)份。这筐橘子共有(
)份
小班分得的橘子个数是大班的(
),
大班分得的橘子数是小班的(
),
大班的分得得橘子数占这筐橘子的(
),
3
2
5
小班的分得得橘子数占这筐橘子的(
),
把这些橘子分给大班和小班,怎么分合理?
如果有140个橘子,按3︰2又应该怎样分?
大班占3份
小班占2份
大班占
5
3
小班占
5
2
140个
3
+2=5
140×
=56(个)
5
2
140×
=84(个)
5
3
李明与黄华合办股份制食品有限公司,李明出资10万元,黄华出资20万元,两年后盈利90万元,怎样分配利润才合理?
在工农业生产和日常生活中,常常需要把一个数量按照一定的比来进行分配。这种分配方法通常叫做按比例分配。
第一步:求平均分的总份数
第二步:用除法求每部分是多少?
第三步:按照每部分占几份用乘法求出每部分是多少。
转化成
按比例分配应用题一般步骤:
解法一·:
分什么,有多少?
总数量
怎样分?
()︰()︰()
求平均分的总份数
求每部分占总数量的几分之几是多少?
用分数乘法求出每部分是多少。
转化成
按比例分配应用题一般步骤:
解法二:
务必掌握的四种类型的题目:
题型1:已知总量,各部分量之间的比求部分量
题型2:已知一个部分量及它与另一个部分量的比,求另一个部分量
题型3:已知一个部分量及它与另一个部分量的比,求总量
题型4:已知两个部分量的比以及差,求部分量或总量
试一试
小清要调制2200克巧克力奶,巧克力与奶的质量比是2︰9。需要巧克力和奶各多少克?
2+9=11
2200×
=400(克)
11
2
答:需要巧克力400克,奶1800克。
2200×
=1800(克)
11
9
试一试
小清要调制2200克巧克力奶,巧克力与奶的质量比是2︰9。需要巧克力和奶各多少克?
2+9=11(份)
2200÷11=200(克)
200
×2=400
(克)
200
×9=1800
(克)
答:需要巧克力400克,奶1800克。
六年级男生人数与女生人数的比是4:5,男生有16人,女生有多少人?六年级共有多少人?
16÷4=4(人)
4×5=20(人)
20+16=36
(人)
答:六年级有女生20人,共有36名学生。
一种什锦糖是由奶糖、水果糖和酥糖按
照2︰5︰3混合成的。要配制这样的什锦
糖500千克,需要奶糖、水果糖和酥糖各
多少千克?
用48厘米的铁丝围成一个长方形,这个长方形长和宽的比是5∶3,这个长方形长和宽各是多少?
48÷2=24(厘米)
5+3=8
答:这个长方形的长是15厘米,宽是9厘米。
24×
=15(厘米)
8
5
24×
=
9
(厘米)
8
3
用120厘米的铁丝做一个长方体的框架。长、宽、高的比是3:2:1。这个长方体的长、宽、高分别是多少?体积是多少?
5-3=2(份)24÷2=12(个)
5+3=8
(份)12×8=96(个)
体育用品商店里排球比篮球少24个,排球与篮球个数的比是3:5,排球和篮球一共有多少个?
本课小结
能运用比的意义解决按照一定的比进行分配的实际问题,进一步体会比的意义。
